Алгоритм поиска оптимальных усилий для лечения двусторонней расщелины твердого нёба

Расщелина верхней губы и нёба является самым распространенным врожденным пороком развития челюстно-лицевой области. По данным статистики различных стран мира, число детей, рожденных с врожденной патологией зубочелюстной системы, в среднем составляет от 1 на 500 до 1 на 1000 новорожденных. Имеется тенденция к увеличению частоты рождаемости детей с данной патологией [3, 15].

Наличие расщелины верхней губы и нёба у новорожденного приводит к множественным функциональным нарушениям, связанным в том числе с жизненно важными функциями дыхания, сосания и глотания. При аномалиях лицевого скелета нарушается нормальная функция твердого нёба – оптимальное распределение напряжений, возникающих в области верхней челюсти в процессе деятельности жевательного аппарата при создании пищевого комка. Процесс жевания оказывается неспособным дать нормальное распределение сил в костной системе, что, в свою очередь, ведет к перегрузке и недогрузке во всех элементах системы [1, 2, 4, 5, 20].

По мере роста ребенка расщелина создает ощутимые препятствия к его социальной адаптации за счет наличия косметического дефекта и нарушения речи. Это служит поводом к запуску процесса стигматизации, определяющего предвзятое отношение к ребенку общества, а нередко – и собственных родителей.

Идеальная методика лечения врожденных расщелин нёба продолжает оставаться источником дискуссий. Очевидно, что использование наугад подобранных методов лечения приводит к высокой частоте неудач повторных операций по устранению расщелины (необходимость реоперации – до 44% случаев) [22].

Методики лечения разнообразны, однако большинство российских авторов высказывают мнение о пошаговой предоперационной ортопедической реконструкции врожденных дефектов верхней челюсти у детей [8, 9, 13, 14, 16, 20]. Ведущим этапом лечения в данном случае является механическое воздействие ортопедических аппаратов на разобщенные нёбные фрагменты с целью уменьшения костного дефекта твердого нёба.

Описание моделируемой методики лечения

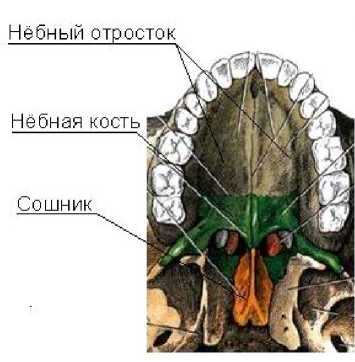
Для удобства восприятия читателем методики лечения приведем на рис. 1 названия и расположение основных костей твердого нёба. Отметим, что межчелюстная кость на рис. 1 не обозначена, поскольку она имеется у человека до четырех лет, а потом срастается с костями верхней челюсти.

В настоящее время в отечественной практике широко применяются съемные ортопедические аппараты со вспомогательной внеротовой эластической тягой, раннее ортопедическое лечение детей с врожденной расщелиной губы и нёба проводят в два этапа. Первый этап начинается с момента рождения ребенка и длится до четырех месяцев, его цель – подготовка к хейлопластике (коррекция формы губ). На втором этапе ортопедического лечения (период после хейлопластики) идет подготовка к уранопластике (устранение расщелины).

При первом посещении врача-ортодонта проводится обследование ребенка, определяется группа сложности деформаций основного порока, с верхней и нижней челюстей слепочной ложкой получают оттиски. Далее по рабочему слепку отливают гипсовую модель, из пластмассы изготавливают корректирующий аппарат, моделируя направляющие для межчелюстной кости и сошника.

Аппарат устанавливают в полость рта малыша. Вся конструкция плотно прилегает с нёбной стороны к буграм и альвеолярным отросткам верхней челюсти по всей длине, а также к нёбным отросткам и сошнику. Одновременно изготавливают шапочку, плотно охватывающую голову ребенка. К шапочке пришивают пуговицы для фиксации эластичного трубчатого бинта на уровне основания крыла носа и угла рта. Фиксация бинта помогает смещению межчелюстной кости к оси симметрии. После адаптации младенца к аппарату каждые 1–2 дня проводят коррекцию ложа межчелюстной кости и сошника путем наслаивания пластмассы с одной стороны и сошлифовывания с другой, приближая их положение к оси симметрии лица. Коррекцию продолжают до тех пор, пока межчелюстная кость вместе с сошником не займет правильное анатомическое положение.

а

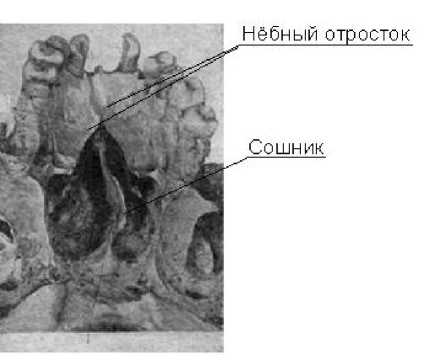
Рис. 1. Твердое нёбо в норме ( а ) и при патологии ( б )

б

Чем раньше предпринято ортопедическо-ортодонтическое лечение, тем оно эффективнее, тем лучше достигаемые функциональные и эстетические результаты, тем быстрее и совершеннее будет выполнена хейлопластика [8, 9, 13]. Такая возможность обусловлена имеющимся у ребёнка значительным потенциалом роста челюстных костей, хотя и несколько сниженным по сравнению со здоровыми детьми. Кроме того, необходимо достичь равновесия в действии губ, щёк, языка, жевательной и мимической мускулатуры, т.е. между силами, которые благотворно влияют на рост челюстей, с помощью ортопедических аппаратов (до операций на верхней губе и нёбе), а в послеоперационном периоде – ортодонтических аппаратов. При этом данная перестройка протекает легче в течение временного и сменного прикуса, пока не произошли стойкие морфологические изменения в тканях челюстно-лицевой области из-за имеющихся послеоперационных рубцов [16].

После проведения хейлопластики через 3–4 недели на очередном приеме у врача-ортодонта начинается второй этап ортопедическо-ортодонтического лечения. Снова получают оттиск с верхней челюсти ребенка с помощью эластичной массы. Далее по оттиску изготавливают гипсовую модель и производят ее предварительную корректировку: на гипсовую модель в области прилегания нёбных отростков наслаивают воск, что позволяет сформировать пространство для перемещения концов нёбных отростков в сторону ротовой полости, а также учесть их рост. Далее по гипсовой модели из зуботехнической пластмассы изготавливают ортопедический аппарат. Его ложе плотно обхватывает сошник. В полости рта аппарат удерживается за счет прилипания в зонах контакта с нёбными отростками.

Давление на отростки со стороны аппарата возникает за счет сил прилипания и работы мощного мышечного органа – языка. Кроме того, пластинка препятствует проникновению языка в расщелину. Поскольку ребенок до хейлопластики пользовался аппаратом, он быстро привыкает к этой конструкции и после нее.

Так как по мере роста нёбные отростки все ближе прижимаются к поверхности аппарата, то корректировка путем спиливания излишков пластмассы со стороны, обращенной к нёбным отросткам, позволяет постепенно формировать свободное пространство под поверхностью нёбных отростков и под их краями. В результате края нёбных отростков всегда свободны, что стимулирует их рост и ускоряет процесс сужения расщелины. Благодаря этому нёбные отростки приобретают форму, обусловленную физиологическими особенностями верхней челюсти ребенка. В результате формируется физиологический для данного пациента свод нёба.

Кроме того, поскольку аппарат полностью закрывает расщелину, устраняется действие языка на ее область, тем самым исключается дальнейшее увеличение крутизны нёбных отростков. Это позволяет быстрее закрыть или уменьшить расщелину нёба и тем самым приблизить сроки проведения уранопластики.

Предварительная корректировка гипсовой модели с помощью воска и аппарата в процессе лечения больного путем спиливания пластмассы позволяет использовать один и тот же аппарат на всем протяжении второго этапа лечения. Применение одного и того же аппарата после хейлопластики до уранопластики повышает физиологичность способа и исключает новые адаптационные периоды, возникающие при коррекции аппарата путем его замены. Следует еще раз подчеркнуть, что продолжительность II этапа ортопедическо-ортодонтического лечения зависит от степени тяжести деформации верхней челюсти и занимает не менее шести месяцев.

Схематически последовательность результатов этапов ортопедического лечения приведена на рис. 2 и 3.

Очевидно, что ортопедические аппараты позволяют опустить нёбные отростки из практически вертикального состояния до положения, при котором последующее зашивание нёба вызывает незначительные деформации зубочелюстной системы.

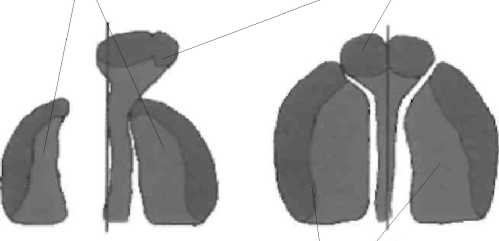
Нёбный отросток Сошник

Нёбный отросток \ а                б

Рис. 2. Положение фрагментов нёба до ( a ) и после ( б ) первого этапа раннего ортопедического лечения

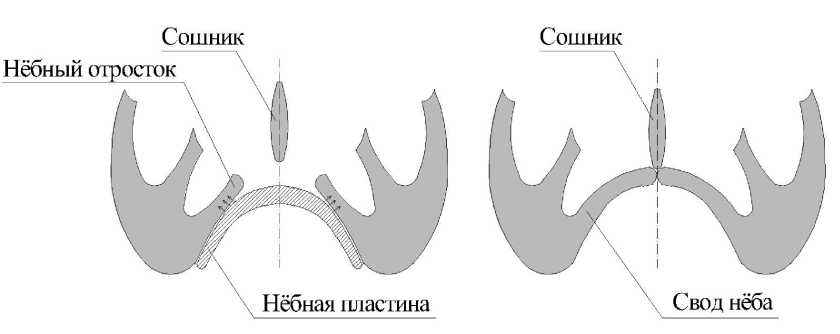
б

а

Рис. 3. Положение фрагментов нёба до ( a ) и после ( б ) второго этапа раннего ортопедического лечения

К сожалению, ортопедическое лечение основано на эмпирическом опыте и субъективных представлениях врачей о ростовых процессах в костной ткани – не существует научно обоснованных стандартов лечения, которые определяли бы для каждого пациента индивидуально эффективный способ достижения наилучших результатов.

По мнению авторов, качество лечения данной патологии должно непременно возрастать вследствие исследования методами математического моделирования влияния ортопедических аппаратов на костную ткань, а именно измерения величины воздействия аппарата у каждого конкретного пациента. В таком случае результативность и действенность конкретного метода лечения будет являться следствием научного подхода к данной проблеме.

Таким образом, развитие биомеханической теории ортопедической реконструкции расщепленного твердого нёба является актуальной и практически значимой задачей в выработке критериев оптимального проектирования ортопедических аппаратов управления ростом нёбных отростков.

Задача управления ростовыми деформациями

В данной работе задача о лечении врожденной расщелины твердого нёба рассмотрена как задача о поиске усилия F , создающего в теле заданную ростовую деформацию. Заданная ростовая деформация способствует формированию нёбной дуги (обозначена пунктирной линией на рис. 4). Величина задаваемых перемещений определяется по чертежу формы дуги, которую хотели бы получить в результате лечения. ISSN 1812-5123. Российский журнал биомеханики. 2012. Т. 16, № 3 (57): 42–56                      45

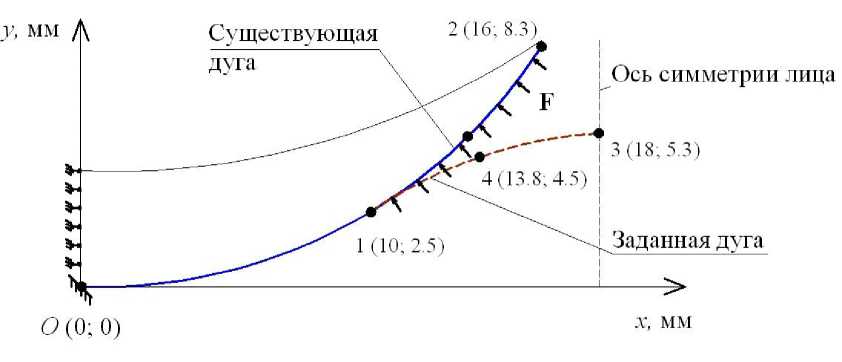
Рис. 4. Заданная ростовая деформация

Следует отметить, что управление ростом уместно на втором этапе раннего ортопедического лечения, когда фрагменты нёба выровнены относительно оси симметрии лица.

Определяющее соотношение биомеханической модели роста Хсю, используемое в данной статье, подробно описано в работе [6]:

§g = A + B--a,(1)

где A – тензор второго ранга, определяющий генетический рост ткани; B – тензор четвертого ранга, характеризующий влияние напряжений σ на деформации скорости роста ξ ^g . Для изотропного материала тензоры A и B можно упростить:

A = AI, B = B C-1,(2)

где I - единичный тензор второго ранга, C ^{- 1} - тензор упругой податливости, A и B -скалярные параметры, определяющие рост ткани. С учетом (2) формула (1) принимает вид

§ g = AI + B £ e,(3)

где ε ^e – тензор упругой деформации.

Рассмотрим далее математическую постановку задачи ортопедического лечения.

Известно, что фрагмент твердого нёба состоит из двух частей (рис. 5): податливой хрящевой ткани (область V ₂ ), соединенной с более жесткой костной структурой (область V ₁ ) [19]. Конкретизация областей должна приниматься на основе томографических данных. В исследуемой модели граница областей принята условно, так как данный расчет не привязан к конкретному пациенту. Геометрические параметры области находятся в физиологическом диапазоне, их величину можно оценить по координатам точек.

Полная дифференциальная постановка задачи растущего упругого тела, занимающего область V в R ^Зс границей S , V = V о S , S = S_v о S _со S_p , S_p = S_p 1 о S_{p 2} (угловые точки (0; 0) и (0; 4) не входят в границы S_v и S _с ), такова:

– определяющее соотношение для ростовой деформации (3);

– деформация ε является суммой упругой ε ^e и ростовой ε ^g деформаций

£ = £ e + £ g ;                                           (4)

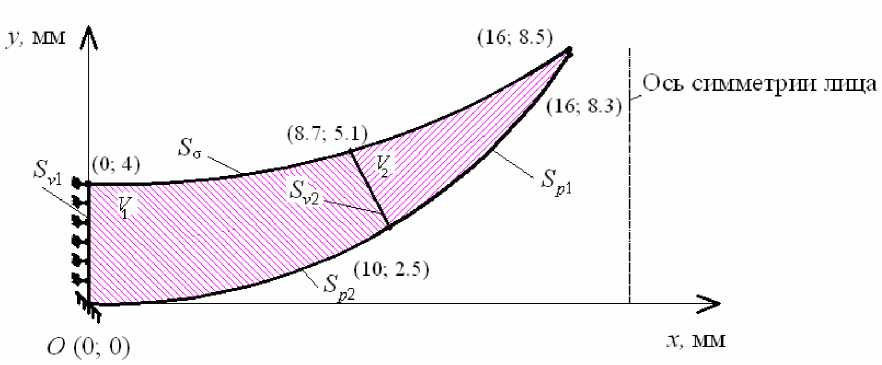
Рис. 5. Расчетная область

– уравнение равновесия

V • о = 0, r е V;(5)

– геометрическое соотношение

^ = 2 (Vv + vV), r е V;(6)

– граничные условия

Vx = 0, тxy = 0, r е Sv,(7)

v = 0 (x = y = 0),(8)

n• о = 0, r е Sc,Sp2, n• о = F, r е Sp j

– начальные условия

u(r,0) = 0.(10)

Уравнения (3, 4–10) позволяют рассчитать накопление ростовой деформации с течением времени во фрагменте, если известны усилия F на границе S_{p 1} .

Отметим, что после снятия ортопедического аппарата нагрузки F также снимаются. После этого во фрагменте остается накопленная ростовая деформация ε ^g , вычисляемая на основе формулы (6). Необходимо подобрать такие усилия F на границе S_{p 1} , чтобы отросток с ростовой деформацией принял форму, показанную на рис. 3, при этом в отростке не должно остаться макроскопических остаточных напряжений.

Применение теории независимого управления деформациями

К РЕШЕНИЮ ЗАДАЧИ

С точки зрения механики, поставленная задача является задачей независимого управления деформациями системы с помощью собственной деформации [7, 10, 12, 17, 21]. Под собственной деформацией в данной работе будем понимать ростовую деформацию в уравнении (4).

Для задачи теории упругости с собственной деформацией доказана теорема о декомпозиции собственной деформации на составляющую, свободную от напряжений е * , и составляющую, свободную от деформаций е * [21]:

е * = е U + е ; .                                         (11)

Анализ собственных деформаций проводится в терминах энергетического линейного гильбертова пространства H с использованием следующих правил вычисления скалярного произведения и нормы:

( е * , е 2 ) = J е ^ - С -- е 2 dV , е * , е 2 е H ,                          (12)

V

II е’| H = ^M H .

Показано, что свободные от напряжений собственные деформации e U образуют подпространство H_u , а нильпотентные собственные деформации – подпространство H _; . При этом подпространства H u и H _; взаимно ортогональны:

(е * , е !) = 0, V e * е H , Е * е Н . и ;                 и и ;      ;

В работе [18] доказана теорема, что для любой собственной деформации е U е H u можно подобрать силы, создающие в таком же упругом теле деформацию е e = е * .

На основе данной теоремы можно сделать вывод, что ростовая деформация, вычисляемая по формуле (3), не будет вызывать остаточных напряжений во фрагментах. Действительно, при граничных условиях (7), (8) однородное расширение A I dt не будет вызывать напряжений, деформация B ε ^edt также не будет вызывать напряжений, так как может быть создана силами в упругом теле.

Таким образом, остается разработать алгоритм поиска необходимых усилий F на границе S_p . Для этой цели предлагается использовать следующий функционал:

Т( F , T ) = J ( е g ( F , T )- е ⁽⁰⁾ ) -- С •• ( е g ( F , T )- е ⁽⁰⁾ ) dV ^ inf ( F , T ) ,          (13)

V где ε(0) – желаемая ростовая деформация, формирующая необходимую форму нёбного фрагмента (рис. 4).

Решение задачи (13) позволит вычислить необходимые усилия F и время их действия T , т.е. период ортопедического лечения.

Алгоритм решения задачи

Для решения поставленной задачи необходимо сначала вычислить желаемые ростовые деформации ε ⁽⁰⁾ . Для этого решим задачу теории упругости для той же области V , задавая необходимые перемещения на границе S p 1 , при этом сохраняя прежние граничные условия на границах S_v , S p ₂ и S _; . Согласно теореме [18] вычисленная деформация фрагмента будет принадлежать подпространству H_u .

Рассмотрения проводятся в рамках конечно-элементной модели, где используются плоские треугольные элементы с линейной аппроксимацией перемещений. Количество элементов обозначено как e . Рассматривается плосконапряженное состояние.

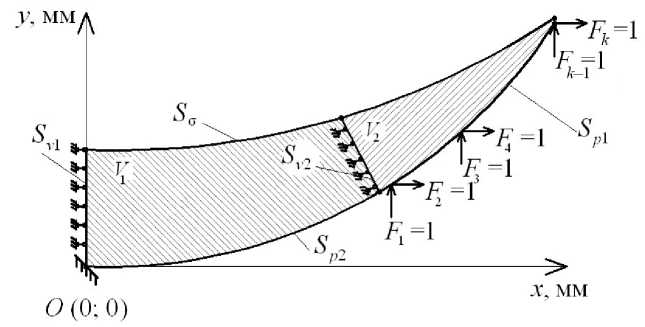
Рис. 6. Область приложения единичных сил

Тогда граница S_{p 1} разбивается на узлы. Если к узлу на этой границе приложить единичную силу F 1 = 1, то можно вычислить ростовую деформацию, соответствующую второму слагаемому в формуле (3),

§g = bt £(1), где £(1) - упругая деформация, вызванная силой F1 = 1.

Таким образом, последовательно прикладывая силы ко всем узлам границы S p 1 , вычислим тензоры £ ^{( к} ) , где к = 1... K (см. рис. 6).

Отметим, что напряжения влияют на рост только в области V ₂ , чтобы это учесть при вычислении £ ^{( к} ) граница S_v 2 считается закрепленной, тогда £ ^{( к} ) = 0, r е V 1 .

В этом случае ростовая деформация, создаваемая в ткани, может быть представлена в следующем виде:

£ g = AT I + ^^F_kBT £ ^{( к} ) ,                             (14)

к = 1

где T – время действия ортопедического аппарата.

Преобразуем целевую функцию (13), раскрывая квадрат нормы:

¥ = J(£g (F)-£(0) )-С ••(£g (F)-£(0) )dV =

^V                                                 ,                    (15)

= ( £ g ( F ) , £ g ( F ) ) h - 2 ( £ g ( F ) , £ '»' ) h + ( e'» ),_E™ ) h

Отбросим слагаемые, не зависящие от F_k , к = 1 _ K , подставим (14) в (15)

*( F ) = ( £ g ( ^F ) , £ g ( F ) ) h - ² ( £ g ( F ) , £ ^|0 > ) h =

= T^{1 f} A I + f. F.B Е ^{| к} ' , A I + K O £^{k 1} ) - 2 T f A I + Y f.B £ ^{| к} ' , г ¹⁰¹ 1 = kkk

V       к=1                   к=1           7 H       V       к=1

KKK

= T ² ( A I , A I ) _H + 2 T ² 1 A 1 , 2 F k B £ ^{( к )} | + T ² 1 £ F k B £ ^{( к} ) , £ F k B £ ^{( к )} | -

V к=1           7 H V к=1            к=1

• - 2 T ( A I , £ ⁽⁰⁾ )_fl - 2 T ^f £ F_k B £ ^{( к} ) , £ ⁽⁰⁾ | .

• н      Vк=1

Поменяем порядок вычисления суммы и скалярного произведения:

KK              K

* = T ² B ² SS F k F i ( ^E ( k ) , ^{E < l )} )„ - ² BT 2 £ F k ( ^E™ / T - A I , ^E“ ’ )„ + k = 1 l = 1                       H             k = 1                                 H

+[ A ² T ² ( I , I ) „ - ² AT ( I , E ⁽⁰ ’ ) „ ] .

В матричных обозначениях формула (16) принимает вид

¥ = T ² B ² { F } ^T [ H ] { F }- 2 T ² B ² { F } T {0}+ у , 1 x K K X K K x 1              1 x K K x 1

где

{ F } = { FF i , - . F K } ,

[ H ] =

( E" ' , E"' ) „ ( E (2' , E" ’ ) h

( E" ' , E ( ² ' ) h

( E¹¹', e“’ ) h

( E ( K' , ^E 1' ) h

( E ⁽ K ' , E ( ² ' ) h

( E^ E'K ' ) h ( E ( ² ' . ‘ ' ) h

( ‘ ' , ‘ ' ) „

{0}= 1- { ( E ¹⁰ ' / T - A I , E ¹¹ ' )_я , ( e'“' / T - A I , E ¹² ' )_B , _ (E^,o ' z T - A I , E K ' )_я } .    (20’

Y = A ² T 2 ( I , I ) H - 2 AT ( I , e^{1 0} ' ) H .                             (21’

Слагаемое ε ⁰⁾ / T в формуле 20) по физическому смыслу представляет собой желаемую скорость ростовой деформации. Матрица [H] в формуле 19) является положительно определенной [7] в силу линейной независимости полей ε ^{k )} .

Таким образом, задача поиска оптимальных усилий { F } сводится к минимизации функции 17), что можно сделать, используя аналитические условия экстремума:

ач7

-- = 0, k = 1,2,_,K .(22’ aFk

Подстановка функции 17) в условия 22) дает систему линейных алгебраических уравнений относительно вектора неизвестных сил { F } :

[H]{ F }-{0} = 0.(23’

K X K K X 1 K X 1

Решение системы (23) может быть найдено с использованием метода обратной матрицы:

{F } = [H]-1 {0}.(24’

K X 1     K X K K X 1

Для того чтобы воспользоваться формулой (24), необходимо найти время действия сил T , которое входит в столбец {0} .

Для дальнейших вычислений удобно представить вектор-столбец {0} в виде

{е} = { е ^(1- } / вт — { е ^(2- } / в ,

где

{ е ⁽¹⁾ } k = ( e* e ¹») H , { е^{1 2} ' } = ( a i ,_E' ^k - ) H , k = 1,2,..., к .

Тогда формула (24) примет вид

A

{f} = [н]-1 |{е(1)}/т —{е(2-} /в.

к х 1     к х к  V к х 1          к х 1 у

Подставим решение (27) в целевую функцию (17):

^ = т ² в ² ( { е^{0 -} } ^т / т — { е ^(2- } ^т

V   1 х к            1 х к  у

/ в [ н ]^— [ н ][ н ]^— I { е ⁽¹⁾ } / т — { е ⁽²⁾ } / в к Х к  к Х к к Х к  V к Х 1          к Х 1 у

—

— 2 т ² в ² ( { е^{0 -} } ^т / т — { е ⁽²⁾ } ^т

V   1 Х к           1 Х к  у

/ в [ н ]^— I { е ⁽¹⁾ } / т — { е ⁽²⁾ } / в + к Х к  V к Х 1          к Х 1 у

+A2т2 (I,I)H — 2Ат(I,E(0) )„ или т = a2т2 (i,i)H — 2ат(i,e(0) )я — т2 Г{е(1)}т/т—{е(2)}т [н]—1 Г{е(1)}/т—{е(2)}

V 1 Х к           1 Х к у ^{к Х к} V к Х 1          к Х 1 у

^ = т

а ² ( I , I ) H — { е ²¹ ) ^т [ н ] { е ^2- } 1 х к    ^{к Х к}     к Х 1

— 2 ^т ( A ^{I ,} E™

) „ "Г } ^т [ н ]^{— 1} ( 0^ю )

1 х к ^{к Х к}      к Х 1

—

— { е ⁽¹⁾ } ^т [ н ]^{— 1} { е ⁽¹⁾ } .

1 Х к    ^{к Х к}     к Х 1

Далее составим уравнение для определения времени действия нагрузки T , дифференцируя целевую функцию (28),

”= 0

5 т и получим формулу для времени T :

( а I ^, E ⁽⁰ - ) H -{0 '" } ^т [ н ]^{— 1} { е ( ² > } ^т                                                      .