Алгоритм поиска точечных подмножеств и его применение для анализа атомной структуры модельных кластеров

В задачах структурного анализа, атомную структуру вещества, часто интерпретируют как множество точек трехмерного пространства. Также с каждой точкой такого множества, сопоставлено некоторое целое число t , соответствующее типу атома или иона. При таком подходе модель структуры вещества описывается множеством наборов вида {ti, xi, yi, zi}, где ti - тип частицы, a Xi, yi и zi - ее координаты. Временную эволюцию такой системы можно отследить с помощью молекулярно-динамического эксперимента, в результате проведения которого будут известны не только термодинамические параметры этой системы, но и координаты всех составляющих ее частиц.

Для оценки степени упорядоченности проэволюционировавшей системы необходимы алгоритмы, позволяющие найти в этой системе координационные многогранники и получить данные об их взаимном расположении такие, как информация о соседствующих многогранниках и об объединении таких многогранников в группы. Под соседством в данном случае понимается наличие у двух многогранников общей вершины, ребра, или грани. В зависимости от количества, соседей можно выделить несколько типов координационных многогранников. В частности, для описания структуры силикатных расплавов и стекол в настоящее время широко используют [1, 2] структурные единицы Qn - кремниево-кислородные тетраэдры SO 4, г де n - число мостиковых(принадлежащих двум атомам кремния) атомов кислорода. Такой подход может быть распространен на. любые типы координационных многогранников. В соответствии с этим, многогранники, не имеющие соседей, будем называть многогранниками типа Q 0, имеющие одного соседа - Q 1, двух со седей - Q ² и так далее.

В данной статье представлен результат исследования по разработке метода, анализа, атомной структуры кластеров, формируемых при компьютерном моделировании неупорядоченных систем. Данный метод основывается на. анализе информации о взаимном расположении координационных многогранников, описываемых конечным набором точек. Для поиска этих многогранников предложен алгоритм, позволяющий в произвольном конечном множестве точек выявить подмножества, которые совпадают при наложении с некоторым заранее определенным набором точек (шаблоном). При этом поиск производится с учетом заданного допустимого отклонения расстояний между точками. Также рассмотрены простейшие способы анализа результатов поиска, в основе которых лежит рассмотрение графа, вершины которого соответствуют найденным координационным многогранникам, а ребра – их соединениям посредством общих вершин, ребер, граней.

Реализованная программа позволяет производить поиск координационных многогранников в компьютерной модели атомной структуры кластера, строить соответствующий граф и рассчитывать численные параметры, характеризующие его структуру. Программа состоит из двух модулей: модуля поиска точечных подмножеств и модуля анализа результатов поиска.

1.    Существующие методы анализа структуры вещества

Решению задачи исследования структуры компьютерных моделей систем атомов посвящено множество работ. В работе [3] описан алгоритм сопоставления точечных множеств, позволяющий выявить степени различия или подобия упорядоченных структур. Для анализа неупорядоченных систем часто используется функция радиального распределения атомов g(r), определяющая плотность вероятности нахождения какой-либо частицы на расстоянии r от некоторой исходной частицы. Однако, для аморфных тел функция g ( r ) затухает при некоторых значениях r _k , называемых дальностью корреляции, и поэтому удобна для описания только ближнего порядка. В работах [4, 5] для исследования компьютерных моделей жидкости и аморфных тел применялась разностная радиальная функция распределения, позволяющая оценить характер дальних осцилляций.

Также удачным средством для исследования структуры жидкостей оказался подход, основанный на геометрических методах Вороного-Делоне [6]. Многогранник Вороного является непосредственным геометрическим образом ближайшего окружения атома, вершины этого многогранника являются центрами симплексов Делоне, заполняющих пространство без зазоров и наложений. При использовании этих методов для анализа структуры рассматриваются различные метрические характеристики многогранников Вороного и симплексов Делоне. В работе [7] в качестве количественной характеристики формы симплекса используется длина его самого длинного ребра; в работах [5, 8] используются индексы тетраэдрич-ности и октаэдричности, характеризующие форму симлекса; в монографии [6] в качестве метрических характеристик многогранника предлагается использовать его объем, площадь поверхности и коэффициент сферичности.

В теоретической химии для изучения молекулярной структуры применяются такие математические теории, как топология и теория графов. С формальной точки зрения структура молекулы интерпретируется как граф, вершины которого соответствуют атомам, а ребра - связям. Различные инварианты (топологические индексы) этого графа зависят от структуры, поэтому производятся попытки увязать их значения с теми или иными физикохимическими свойствами различных веществ [9, 10].

2.    Постановка задачи

Формально задача поиска точечных подмножеств состоит в следующем.

Пусть в n-мерном евклидовом пространстве En заданы два конечных множества точек X и Y , также задано некоторое конечное множество натуральных чисел M ⊂ N. Причем каждой точке множеств X, Y поставлено в соответствие некоторое натуральное число t ∈ M , обозначающее тип этой точки. Множество Y будем называть шаблоном поиска. Задача состоит в том, чтобы найти все такие подмножества X G X, равномощные с Y, чтобы при наложении друг на друга множества X и Y совпадали с точностью до некоторого заранее заданного положительного вещественного числа ε. При этом, будем считать равномощные множества X и Y совпадающими с точностью до ε, если из элементов множества X можно составить последовательность {Xi}, а из элементов множества Y - последовательность {yi}, так, чтобы t-i = tyi, а Ip^X^xj) — p(yi,yj)| < Е для любых допустимых i, j.

3.    Поиск точечных подмножеств

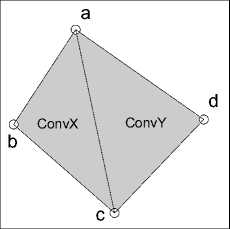
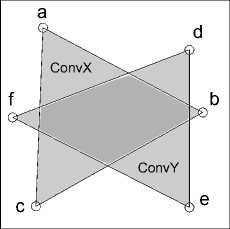
Решение поставленной задачи представляет собой некоторый набор искомых подмножеств исходного точечного множества. Расположение этих подмножеств в пространстве может быть произвольным: они могут иметь общие точки, либо не пересекаться. Однако, для поиска коорднационных многогранников требуются дополнительные ограничения на взаимное расположение найденных подмножеств в пространстве. Например, для этой задачи недопустимо их перекрывание (рис. 1, г), т.к. в этом случае возникает неопределенность в том, какое из найденных подмножеств является координационным многогранником.

Определение 1. Будем говорить, что два точечных подмножества X, Y С E n перекрываются, если пересечение относительных внутренностей их выпуклых оболочек не пусто, то есть riConvX П riConvY = 0.

б

г

Рис. 1. Варианты взаимного расположения точечных множеств на плоскости

На рис. 1 представлены некоторые варианты взаимного расположения двух точечных множеств X и Y на плоскости: (а) - множества X = { a, b, c} и Y = {d, e, f } не пересекаются; (б) – множества X и Y и их выпуклые оболочки C onvX и ConvY пересекаются в точке b ; (в) – множества X и Y имеют две общие точки a и c , а их выпуклые оболочки - отрезок [ a, c ] ; (г) - множества X и Y не пересекаются, но перекрываются в смысле определения 1.

Частично решить проблему перекрывающихся подмножеств можно путем введения некоторого условия, позволяющего выделить из всех перекрывающихся подмножеств одно, ≪ наиболее подходящее ≫ . Например, при поиске треугольников на плоскости таким критерием может служить радиус описанной окружности. Так, если будет найдено несколько пересекающихся треугольников, то в соответствии с этим критерием выбрать нужно будет тот, радиус описанной окружности которого наиболее близок к радиусу описанной окружности шаблонного треугольника. Для точечных множеств более сложной конфигурации вместо радиуса описанной окружности, например, можно использовать диаметр множества, определяемый как sup_x,_yEM p(x,y), где M С E n .

Алгоритм поиска .

Входные данные: массив X , содержащий координаты и тип точек, среди которых будет производиться поиск; массив Y , содержащий координаты и тип точек, составляющих шаблон поиска; вещественное число ε , определяющее допустимое отклонение расстояний между точками.

Выходные данные: двумерный массив R , каждая строка которого содержит номера точек входного массива X , совпадающих с шаблоном поиска с максимальным отклонением расстояний ε .

Шаг 1. Формируем матрицу расстояний (rij ) , где rij - расстояние между i -ой и j -ой точками массива Y , и определяем пустой массив R для хранения результатов поиска;

Шаг 2. Выбираем из массива Y первую точку y_k ;

Шаг 3. Выбираем из массива X первую точку xi ;

Шаг 4. Если тип точки xi совпадает с типом точки y_k , переходим на Шаг 6;

Шаг 5. Выбираем из массива X следующую точку xi и переходим на Шаг 4;

Шаг 6. Формируем массив F , содержащий один элемент – индекс точки xi в массиве X ;

Шаг 7. Выбираем из массива Y следующую точку y_k ;

Шаг 8. Выбираем из массива X все точки xj , такие, что: индекс точки xj не содержится в массиве F , тип xj совпадает с типом y_k , а расстояния от точки xj до всех точек из X , номера которых содержатся в F , совпадают с соответствующими элементами матрицы расстояний ( r ij) с точностью до е ;

Шаг 9. Если таких точек нет, переходим к Шагу 5. Иначе для каждой точки x j формируем новый массив F _j ^′ , содержащий все индексы точек из массива F , а также индекс точки x j в массиве X ;

Шаг 10. Если все точки из массива Y были выбраны, то в массивах F _j ^′ содержатся результаты поиска – записываем номера точек из каждого массива F _j ^′ в конец массива R и переходим к Шагу 11. Иначе, последовательно обозначая каждый из получившихся массивов F _j ^′ за F , продолжаем выполнение алгоритма с Шага 7;

Шаг 11. Выводим содержимое массива R и завершаем выполнение алгоритма.

Предложенный алгоритм разработан на основе алгоритма сопоставления точечных множеств [3] и реализован в программе, предназначенной для анализа атомной структуры кластеров, формируемых при компьютерном моделировании. Атомные кластеры и координационные многогранники описываются наборами точек в трехмерном пространстве, поэтому разработанный алгоритм может быть применен к решению данной задачи.

4.    Реализация

Для применения предложенного алгоритма к задаче исследования структуры кластеров была разработана программа, состоящая из двух модулей: модуля поиска точечных подмножеств и модуля анализа результатов.

Модуль поиска точечных подмножеств .

Данный модуль предназначен для поиска в массиве, описывающем некоторую систему атомов, заранее определенных структур. В большинстве проводимых экспериментов такими структурами являлись координационные многогранники.

Входные параметры: массив координат и типов атомов, в котором будет осуществляться поиск; массив координат и типов атомов, описывающий шаблон поиска; положительное вещественное число ε , определяющее допустимые отклонения расстояний.

Суть работы модуля заключается в рекурсивном построении подсистем атомов исходного массива, совмещаемых с системой атомов, определяемой шаблоном поиска, операциями параллельного переноса, поворота и зеркального отражения, в соответствии с алгоритмом, изложенным выше.

аб

Рис. 2. Результаты поиска: (а) – кобальт-кислородных октаэдров в структуре оксида кобальта; (б) – кремниево-кислородных тетраэдров в структуре α -кварца

Результатом работы модуля является двумерный массив, каждая строка которого содержит номера атомов, образующих одно из найденных подмножеств. На рис. 2 представлена визуализация результата работы программы. В данном случае производился поиск: (а) – кобальт-кислородных октаэдров в упорядоченной структуре оксида кобальта (CoO); (б) – кремниево-кислородных тетраэдров в кристалле α -кварца. Также работоспособность реализованного алгоритма была проверена на некристаллических структурах (Рис. 3).

В ходе отладки была проведена проверка результатов поиска на корректность. Также оценивалось время выполнения алгоритма в зависимости от размеров обрабатываемых массивов и наличие перекрываемости оболочек найденных подмножеств в зависимости от значения параметра ε .

Оптимальное значение параметра ε определяется целью поиска. Так, например, при меньших значениях параметра можно обнаружить структуры, наиболее близкие к идеальному шаблону, при б´ольших – более деформированные и зачастую перекрывающиеся.

На рис. 3 приведен результат поиска кремниево-кислородных тетраэдров (SiO 4 ): (а) – в структуре жидкого стекла легированного кобальтом Na 2 Si 4 O 10 Co; (б) – в структуре аморфного оксида кремния (SiO 2 ). Длина ребра (связь O –O ) идеального тетраэдра (шаблона) составляет ∼ 2 , 66 ^˚ A, а значение параметра ε принято за 0 , 5 ^˚ A. При таком значении параметра ε лишь незначительная часть найденных тетраэдров перекрывают друг друга, при этом сравнение радиусов описанных сфер перекрывающихся тетраэдров с радиусом описанной сферы шаблонного тетраэдра позволяет отбросить ≪ лишние ≫ тетраэдры и получить более полную информацию о структуре системы атомов по сравнению с информацией, полученной при меньшем значении ε .

Модуль анализа результатов

Данный модуль предназначен для построения графа, описывающего структуру исходной системы атомов на уровне найденных подмножеств (координационных многогранников), а также для расчета инвариантов этого графа, которые, по нашему мнению, могут быть использованы для количественного описания структуры кластеров, формируемых при компьютерном моделировании. Вершины этого графа соответствуют найденным подмножествам, а каждое его ребро – одной общей точке двух пересекающихся подмножеств.

б а

Рис. 3. Результат поиска кремниево-кислородных тетраэдров: (а) – в структуре жидкого стекла, легированного кобальтом; (б) – в структуре аморфного оксида кремния

В общем случае полученную с помощью модуля поиска систему подмножеств можно описать некоторым несвязным мультиграфом. Анализ структуры этого графа с учетом дополнительной информации о найденных подмножествах (например, индекс тетраэдрично-сти [5, 7] для четырехточечных подмножеств), а также расчет различных топологических индексов может быть использован для поиска аналитических соотношений типа структура– свойство.

Входные данные: массив координат и типов атомов, в котором производился поиск (необходим для определения степени искаженности); двумерный массив результатов поиска, полученный с помощью модуля поиска.

Основным результатом работы модуля является массив вершин графа и массив его ребер. На основе этих массивов формируется двумерный массив, описывающий компоненты связности полученного графа. Выводится информация о количестве компонент связности, их средней и максимальной длине. Также для многогранников выводятся данные об их распределении по типам Q ⁰ - Q ⁿ [1].

В таблице приведены характеристики четырех исследуемых кластеров ( α -кварца, жидкого стекла, легированного кобальтом ( Na2Si4O10Co ), аморфного оксида кремния ( SiO2 ) и кристаллического оксида кобальта ( CoO )) и результаты их анализа, полученные с помощью данного программного модуля. Из таблицы видно, что численные характеристики такие как, количество компонент связности и среднее количество вершин в компоненте, сильно разнятся для кластеров в кристаллическом и аморфном состоянии. Для кластеров в кристаллическом состоянии характерно наличие у соответствующего графа только одной компоненты связности, поэтому среднее количество вершин в компоненте совпадает с общим количеством вершин. Графы неупорядоченных кластеров имеют множество компонент связности, многие из которых состоят из одной изолированной вершины. Таким образом, даже простейшие численные характеристики графа, построенного на основе информации о взаимном расположении координационных многогранников, отражают особенности атомной структуры кластера. Расчет и объединение подобных характеристик в более сложные интегральные топологические индексы может быть использован для построения корреляций типа структура-свойство.

Таблица

Результаты анализа различных кластеров

	а -кварц	Na 2 Si 4 O 10 Co	SiO 2	CoO
Количество частиц в кластере	1125	1190	1200	1000
Форма кластера	паралл-д	шар	шар	куб
Диаметр кластера, А	45,6	35,3	33,6	33,1
Площадь поверхности класте-pa, 1000А2	3,2	3,1	2,6	2,2
Объем кластера, ЮООА3	14,1	17,0	11,2	6,6
Доля атомов в поверхностном слое толщиной 2,5А, %	59,4	45,3	53,0	78,4
Тип координационного многогранника	тетраэдр	тетраэдр	тетраэдр	октаэдр
Отклонение расстояний в , А	0,4	0,4	0,4	0,5
Количество найденных многогранников	280	186	185	256
Среднее количество смежных вершин по всем вершинам	3,20	1,80	1,83	9,19
Количество компонент связности	1	33	29	1
Среднее количество вершин в компоненте	280,00	5,64	6,38	256,00
Количество    изолированных вершин ( Q 0)	0	16	20	0
Порядок наибольшей компоненты связности	280	43	140	256

Заключение

В результате данной работы предложен метод исследования атомной структуры кластеров, формируемых при компьютерном моделировании, основанный на анализе взаимного расположения координационных многогранников. Также предложен алгоритм поиска подмножеств в конечных точечных множествах, лежащий в основе данного метода. Он описан в самом общем виде и может быть использован для решения широкого круга задач. Проверка программной реализации этого алгоритма была выполнена на кластерах различной формы, структуры и состава. Анализ результатов работы программы показал, что предложенный метод может быть использован для исследования неупорядоченных атомных систем.

Работа выполнена при поддерэюке Программы стратегического развития (ПСР) ПетрГУ в рамках реализации комплекса мероприятий по развитию научноисследовательской деятельности на 2012 - 2016 гг.