Алгоритм построения интегрального индикатора качества сложной системы для ряда последовательных наблюдений

ОБРАЗЕЦ ЦИТИРОВАНИЯ

Интегральные характеристики качества системы используются при решении задач управления для совершенствования механизмов управления на основании сопоставления интегральных индикаторов рассматриваемых объектов и рейтингов объектов, определяемых их интегральными характеристиками, и являются показателем степени достижения цели управления. Согласно данным ООН, к 2011 году существовало 290 индексов, разработанных для ранжирования или комплексной оценки стран в соответствии с некими экономическими, политическими, социальными или экологическими критериями. Обзор феноменального роста количества применяемых для комплексной оценки стран сводных индексов, проведенного Бандура [13–15], показал, что только 26 из них (9%) было сформировано до 1991 года, 132 (46%) — с 1991 года по 2006 год, а в период 2007–2011 годы было сформировано 130 сводных индексов.

Стремительное увеличение числа композитных индексов является явным признаком их важности в разработке государственной политики и оперативной значимости в макроэкономике в целом. Все основные международные организации, такие как Организация экономического сотрудничества и развития (OECD), Европейский Союз, Всемирный экономический форум или Международный Валютный Фонд конструируют составные показатели в самых различных областях [15, 23]. Общей целью большинства из этих показателей является ранжирование стран и их сравнительный анализ по некоторой агрегированной мере [15, 16, 26, 27]. Возможность использовать в политических целях единый показатель, обобщающий сложные, плохо формализуемые процессы (качество жизни, финансовую устойчивость, рыночную политику и т. д.) является сильным искушением для заинтересованных сторон. Следовательно, улучшение методик построения таких показателей является очень важным вопросом исследования и с теоретической, и с практической точек зрения.

Создатели композитных индексов считают, что сводная статистика действительно адекватно описывает реальность, и такое выделение итога является чрезвычайно полезным в обеспечении интереса средств массовой информации и внимания политиков. С точки зрения противников составных характеристик, достаточно сформировать соответствующий набор показателей, и не имеет смысла идти далее, к получению интегральной характеристики. Их основными возражениями является произвольный характер определения весов, с помощью которых переменные объединяются в единую характеристику. Обсуждение плюсов и минусов составных показателей приводится в работах [16, 23].

Организация экономического сотрудничества и развития (OECD) и развития ведет непрерывную работу по совершенствованию методик построения композитных индексов [23–26]. В 2008 году OECD совместно с Объединенным исследовательским центром (Joint Research Centre European Commission) с подготовлен справочник [17], явившийся итогом многолетних исследований в этой области [23–26, 29], где для широкого круга заинтересованных лиц изложен набор технических принципов, которые должны помочь исследователям в формировании составных показателей. Основным методом агрегации данных авторы выбирают линейную свертку показателей, а основным инструментом построения сводных показателей — факторный анализ.

Для построения качественного интегрального показателя необходима, во-первых, тщательная теоретическая проработка теоретических аспектов измеряемого явления, ибо «то, что плохо определенно, вероятно, будет плохо измерено» [23], во-вторых, качественный выбор данных, так как качество составных индикаторов в значительной степени зависит от качества базовых показателей, и в-третьих, адекватный инструмент для работы с многомерными данными.

Факторный анализ впервые был использован для объединения показателей в единый индекс при разработке индекса здоровья в работе Хайтауэра в 1978 году [19]. При вычислении Показателей социально-экономический статуса (Socio-Economic Status Indices, SES) метод главных компонент был принят в качестве стандарта метода построения, где вычисляемый индекс определяла проекция на первую главную компоненту [22, 30]. Эту же методику использовали Линдман и Селин при создании Индекса экологической устойчивости [21], Сомарриба и Пена при измерении качества жизни в Европе [28]. Среди отечественных исследований следует отметить работы С.А. Айвазяна [1, 2] по определению индекса качества жизни населения.

Однако первая главная компонента хорошо приближает моделируемую ситуацию, если максимальное собственное число ковариационной матрицы дает вклад не менее 70% в сумму всех собственных чисел. Такое соотношение выполняется, если рассматривается небольшое количество признаков (не более пяти), и одно из свойств системы явно доминирует над остальными. При описании социально-экономических систем число пе- ременных значительно более пяти, а структура системы не допускает простого приближения. В качестве выхода из этой ситуации рассматривается согласно [2] понижение порога информативности до 55%, и деление исходной системы на подсистемы, описываемые меньшим количеством переменных. В рассмотренных выше исследованиях [19–22, 28, 30] вклад наибольшего собственного числа колебался от 13% до 38%, за исключением работы [28], рассматривавшей модельный пример, где эта цифра составила 56%. Авторы следовали рекомендациям [28], утверждавшим, что первая главная компонента дает удовлетворительные весовые показатели даже в тех случаях, когда наибольшее собственное число вносит небольшой вклад в сумму всех собственных чисел.

Исследователи Организации экономического сотрудничества и развития придерживаются иной точки зрения. Для формирования составного индикатора используют факторный анализ, где метод главных компонент применяется исключительно для извлечения факторов с тем, чтобы количество извлеченных факторов объясняло бы более 50% общей дисперсии. Значение композитного индекса в этом случае определяют только значимые нагрузки выбранных главных факторов после вращения. Де-факто именно эта методика становится стандартом при вычислении композитных индексов [20, 23, 24, 29]. Хотя авторы [23] обращают внимание, что различные методы извлечение основных компонент и различные способы вращения подразумевают различные значимые переменные, а значит, разные веса переменных при вычислении композита, следовательно, и различные значения вычисляемого интегрального индикатора. Кроме того, факторный анализ предполагает наличие достаточной корреляции между исходными переменными, что в некотором смысле противоречит идее полного описания исследуемого явления совокупностью независимых величин.

Следует также отметить еще одно обстоятельство. Методика определения весовых коэффициентов с помощью факторного анализа не может применяться для сравнения характеристик описываемых объектов в динамике, так как даже при фиксированных методах извлечения факторов и способа вращения, факторный анализ для разных наблюдений системы структуру главных факторов (значимые нагрузки) определяет по-разному, что делает бессмысленным межвременные сравнения [10].

Недостаточное удовлетворение исследователей качеством построенных композитных показателей основывается не только на методических проблемах построения, но и на недостаточном качестве используемых данных, так как фиксируемые статистическими организациями данные неизбежно содержат погрешности измерения. Тем не менее, именно статистические данные, содержащие неустранимые погрешности, в настоящее время представляют собой наилучшие оценки имеющихся реальных величин в социальных системах [18, 23].

Получение точных характеристик объекта на основании однократного измерения, неизбежно содержащего неизвестную погрешность, не представляется возможным. Однако по серии таких измерений вычисление неизвестной характеристики вполне вероятно. Такую задачу, в частности, с успехом решает астрофотометрия, определяющая основные числовые параметры астрономических объектов не по однократному наблюдению (изображению), а по серии зашумленных изображений. Используя основные идеи, лежащие в основе астрофотометрии, будем рассматривать построение интегральной характеристики изменения качества сложной системы как решение задачи выделения полезного сигнала по серии наблюдений, содержащей описание неизвестного параметра (в

Алгоритм построения интегрального индикатора качества сложной системы... многомерном массиве зашумленных данных) в условиях априорной неопределенности о свойствах полезного сигнала на основании задаваемого отношения сигнал/шум .

Целью статьи является разработка методики построения интегральной характеристики изменения качества сложной системы на основании серии регистрируемых измерений с помощью метода главных компонент. В разделе 1 представлена постановка задачи вычисления интегральной характеристики изменения качества системы. В разделе 2 обсуждается вопрос определения информативности решения поставленной задачи при наличии шума в измеряемом сигнале. Раздел 3 посвящен алгоритму построения интегральной характеристики изменения качества системы на основании задаваемого отношения сигнал/шум. В последнем разделе с помощью предложенного алгоритма построены интегральные индикаторы изменения качества жизни субъектов Российской Федерации за 2007–2014 годы. В заключении делается вывод, что предлагаемая методика может быть использована для вычисления интегральных оценок изменения качества плохо формализуемых систем.

1. Постановка задачи вычисления интегральнойхарактеристики изменения качества системы

Рассмотрим построение интегральной оценки системы из m объектов, для которой известны таблицы из n описаний объектов для ряда наблюдений t = 1,2, … — матрицы

A = { a } nm I j i jj = 1

Для каждого момента t вектор интегральных показателей имеет вид qt = A • w t,

t где q

= (q t l , q t 2 ,..., q tm^

вектор интегральных индикаторов момента t,

wt = /wti, wt2, ...,wtm\ — вектор весов показателей для момента t, At — матрица предобработанных данных для момента t. Для построения интегрального индикатора качества системы требуется найти веса показателей wt для каждого момента времени.

Будем рассматривать оцениваемый объект как сложную (не поддающуюся удовлетворительной формализации), большую (число состояний выше современных вычислительных возможностей) систему. Такими системами являются как каждый биологический объект, так и любая социальная система. Система доступна для наблюдения, и известно конечное, достаточно большое число регистрируемых с некоторой точностью численных характеристик этой системы в разные моменты времени. Значимость регистрируемых показателей для функционирования системы в общем случае неизвестна. Для решения задачи управления требуется дать мотивированную оценку каждого наблюдаемого объекта на всем промежутке наблюдений, т.е. вычислить в динамике интегральную характеристику качества системы. Численные характеристики системы предварительно подвергнуты унификации — приведению значений переменных на отрезок [0, 1] по принципу: «чем больше, тем лучше».

Любое измерение, в том числе и статистическое, неизбежно связано с точностью измерительного прибора, поэтому результат измерения неизбежно содержит неустранимую ошибку. Построение интегральной характеристики системы можно рассматривать как задачу выделения полезного сигнала на фоне шумов в условиях отсутствия априор- ной информации о статистических характеристиках аддитивного шума и полезного сигнала при наличии единственной реализации измеряемого процесса. Эта задача аналогична задаче восстановления цифровых изображений, искаженных белым гауссовским шумом. Метод главных компонент (МГК) позволяет выделить структуру в многомерном массиве данных и с успехом применяется для распознавания изображений и для шумоподавления.

Количественные характеристики конкретной системы, функционально связанные с ее структурными особенностями и условиями ее работы, зависят от отношения сигнала к шуму. Это отношение часто используется для количественной оценки эффективности различения сигналов в оптико-электронных, телевизионных автоматических системах, в средствах контроля и диагностики.

ОСШ — отношение сигнал/шум (англ. signal-to-noise ratio, сокр. SNR) представляет собой отношение сигнала (а если точнее, суммы сигнала и шума) к шуму. Величина может быть вычислена либо как безразмерное отношение амплитуды сигнала к амплитуде шума SNR = A s / A n , либо в децибелах SNR ( dB ) = 20 ■ log ₁₀ ( A s / A n ) . Эта величина наиболее полно описывает качество воспроизведения сигнала в телевизионных системах, в системах мобильной связи, в астрофотометрии.

Выбор порогового значения отношения полезного сигнала к шуму фона, позволяющего различить сигнал на фоне шума, обоснован в [8]. Современные технические системы (и человеческий глаз) уверенно выделяют сигнал из шума, если уровень ОСШ системе составляет около 7 дБ (в безразмерных единицах — 2,2). Такое пороговое значение используется в фотометрии слабых объектов: при регистрации сигнала от тусклых звезд необходимо, чтобы отношение сигнал/шум превышало 2,2. Телевизионные системы могут восстановить из шума неповрежденную картинку, если отношение уровня сигнала к уровню шумов превосходит пороговое значение ( SNR _th_r . ) около 7дБ. Именно это значение SNR thr . = 2,2 и будет использоваться далее.

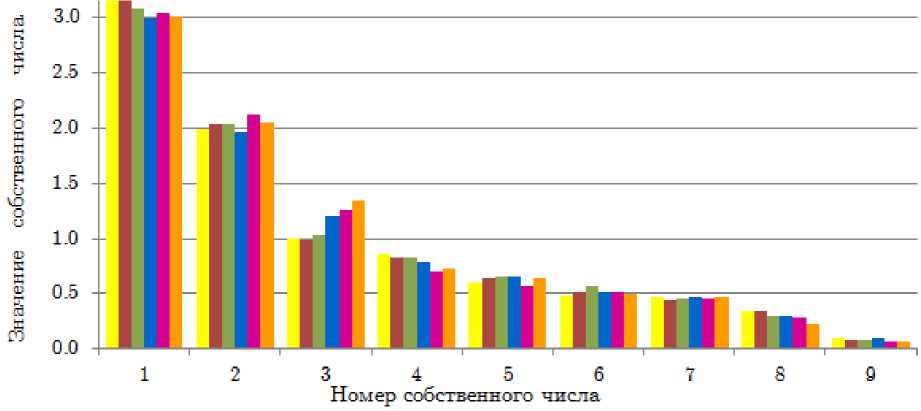
Статистические данные неизбежно содержат погрешность измерения. Любой результат, полученный на основании этих данных, будет содержать неустранимую ошибку. Переход к другому моменту времени означает изменение данных, которое при неизменной структуре системы вызвано как изменением ситуации, так и случайными ошибками. Метод главных компонент на основании различных для разных моментов значений собственных векторов и собственных значений описывает неизменную структуру системы. Следовательно, именно значения собственных чисел и собственных векторов будут тем неизменяющимся сигналом, который нужно распознать, т.е. по имеющимся реализациям выделить сигнал из зашумленных данных. Предположение о том, что при вариации входных данных у собственных чисел имеется общая тенденция, иллюстрирует рис.1, где представлены значения упорядоченных по убыванию собственных чисел для разных наблюдений. В среднем значении рассматриваемых величин хорошо просматривается тенденция (сигнал) и случайное отклонение от нее. Именно усреднение значений используется в астрофотографии для подавления шумов. Усреднение работает на основе предположения об абсолютно случайной природе шума. Соответственно, случайные отклонения от истинных данных будут последовательно снижаться по мере усреднения возрастающего числа наблюдений.

2007       1 2008       1 2000      12010       1 2011      12012

Рис. 1. Собственные значения ковариационной матрицы переменных

для различных моментов наблюдения

Собственные векторы в методе главных компонент определяются с точностью до направления, в отличие от собственных чисел, определяемых однозначно. Среднее значение факторных нагрузок переменных зависит от выбранного направления и не может однозначно характеризовать сигнал. Следовательно, на основе вычисленных для различных наблюдений собственных векторов (упорядоченных в порядке убывания собственных чисел) нужно распознать случайные и неслучайные компоненты этих векторов и определить значения координат неслучайных переменных этих векторов.

Наличием неслучайного (т.е. значимого) вклада переменной в структуру главных компонент будем считать не большую величину факторной нагрузки после вращения, а инвариантность факторной нагрузки при возмущениях, признаком которой будет величина отношения сигнал/шум, определяемая средними значениями переменной (сигнал) и среднеквадратичным отклонением (шум). Если это отношение выше порогового значения, такую переменную считаем неслучайной — действующей. При невыполнении такого соотношения переменная характеризует шумовую составляющую сигнала и не участвует в дальнейшем рассмотрении. Для проверки этого условия нужно согласовать направления собственных векторов на основании некоторого критерия. После согласования направлений главных компонент и определения значимых переменных они, как и в факторном анализе, будут участвовать в дальнейшем рассмотрении, а незначимые переменные игнорируются (обнуляются). Модифицированные по такому принципу главные компоненты будем далее именовать эмпирическими главными компонентами (ЭГК). 2. Информативность интегральной характеристики измене- ния качества системы

В алгоритмах вычисления интегральной характеристики по ОСШ-методу [8–11] используется традиционное для МГК понятие информативности, которое определяет чис ло главных компонент l, используемых для вычисления интегральной характеристики.

Л + Лэ + ... + Л

Y о = —--- ² -------^L ^ 6 .

Л 1 + Л 2 + ... + Л n

Однако размерность пространства признаков в задачах вычисления интегральной характеристики качества сложной системы не является чересчур большой, и вычислительных проблем при определении собственных чисел и векторов не возникает. А каче- ственное описание структуры системы требует либо всех главных компонент, либо их достаточно большого количества. Может оказаться, что ценная для конкретной задачи информация содержится как раз в направлениях с меньшей дисперсией. Например, при создании цифровой модели рельефа, которая строится по оцифрованным снимкам, искомый рельеф дают восьмая и девятая главные компоненты, а главные компоненты 12

и 13 в методе «Гусеница» свидетельствует о наличии в анализируемых данных периодики с дробным периодом [5, 6].

Подходы к оценке числа главных компонент по необходимой доле объясненной дисперсии формально применимы всегда, однако неявно они предполагают, что нет разделения на «сигнал» и «шум», и любая заранее заданная точность имеет смысл. При разделении данных на полезный сигнал и шум задаваемая точность теряет смысл и требуется переопределить понятие информативности. Аналогично дисперсионной информативности согласно (2) можно определить SNR-информативность для выбранного числа эмпирических главных компонент N:

_ Su + S 12 + ... + S i N

^γ SNR                              ^,

S 21 + S 22 + ••• + S 2 N где S1k — сумма величин ОСШ у действующих переменных k-ой ЭГК, S2k — сумма ОСШ всех переменных k-ой ЭГК. Эта величина будет апостериорной оценкой (сверху) SNR-информативности. В отличие от дисперсионной информативности, SNR-информативность не может достигать 100% по логике построения. Информативность выбранной системы признаков определяется дисперсионной и SNR-информативностью:

Y = Y a • Y SNR

3.    Алгоритм построения интегральной характеристики из-менения качества системы как решение задачи выделения полезного сигнала на фоне шумов

Приведем алгоритм построения интегральной характеристики изменения качества системы для ряда наблюдений на основании регистрируемых измерений, который обеспечивает решение задачи выделения сигнала в многомерном массиве данных в условиях априорной неопределенности о свойствах полезного сигнала на основании задаваемого отношения сигнал/шум. Основным параметром алгоритма является пороговое значение отношения полезного сигнала к шуму фона. По умолчанию используется пороговое значение SNR _thr . =2,2, применяемое в современных технических системах и позволяющее различить слабый сигнал на фоне шума. Возможно использование несколько более высокого порогового значения ОСШ, характеризующего именно слабый сигнал — до трех единиц. Если структура системы позволяет из содержательных соображений выделить подсистемы рассматриваемой системы, то переменные, описывающие систему, могут быть объединены в блоки и интегральная характеристика всей системы вычисляется через характеристики подсистем. Входными данными алгоритма являются:

- таблицы из n описаний m объектов для ряда наблюдений t = 1,…, T

—

t t n,m                                  t матрицы A = {ay }   . Элемент матрицы ay — значение j-го показателя i, j=1

i-го объекта, вектор a * = ( a iit

,..., a in¹ )— описание i-го объекта в момент t;

- пороговое значение отношения сигнал/шум SNR _thr . . Алгоритм включает следующие шаги:

• 1    шаг. Подготовка данных

• -    обеспечение однородности выборки и унификация показателей .

Отсутствующие значения для отдельных наблюдений восстанавливаются интерполяцией по имеющимся данным. Устраняются те переменные, которые связаны друг с другом известной функциональной зависимостью (например, из двух переменных — количество мужчин и женщин в процентах — оставляется одна). Для прочих экспериментальных данных строгая коллинеарность практически не наблюдается, и переменные могут участвовать в решении задачи даже при высоких значениях парной корреляции.

Если исходный показатель связан с анализируемым интегральным свойством качества монотонной зависимостью, то при унифицировании исходных показателей (приве- дении их на отрезок [0, 1] по принципу «чем больше, тем лучше») переменные xij для каждого момента наблюдения преобразовываются по правилу:

^aij = sj ⁺ ( ^- 1 ) s j

x _ij

- mj

Mj ^- mj

где sj = 0, если оптимальное значение j - го показателя максимально и sj = 1, если оп- тимальное значение j - го показателя минимально, mj — наименьшее значение j-го показателя по всей выборке (глобальный минимум), Mj — наибольшее значение j-го показателя по всей выборке (глобальный максимум).

Если исходный показатель связан с анализируемым интегральным свойством качества жизни немонотонной зависимостью (т.е. внутри диапазона изменения данного показателя существует значение Xjopt, при котором достигается наивысшее качество), то значение соответствующего унифицированного показателя рассчитывается по формуле:

'

aij ^- 1 ^-

V

__________________I xj xj opt 1__________________ max ((M j - x j opt ), ( x j opt - m j ))

2 шаг. Определение априорных собственных векторов и собственных чисел для каждого наблюдения t

• -    центрирование (стандартизирование) унифицированных переменных: каждый элемент центрированной матрицы данных вычисляется по формуле:

  zi j

  
  

  a ij ^- a j s j

  
  

где a j = — Y a ij — выборочная средняя, s .2 = 1 ^ ( x i . ^m i =1                                                   ^m i =1

x j ) ² — выбо-

рочная дисперсия, т.е. s _j — выборочное среднеквадратичное отклонение;

• -    вычисление по центрированным значениям унифицированных показателей ковариационной матрицы, совпадающей в этом случае с матрицей корреляций;

• -    нахождение для каждого t собственных значений ковариационной (корреляционной) матрицы λ ^t _i , i = 1, …, n, ранжирование их по убыванию;

нахождение собственных векторов, соответствующих собственным числам λ ^t _i для каждого наблюдения: w ^ti = w ^ti1 , w ^ti2 , w ^tin , t = 1,…,T.

3 шаг. Определение эмпирических собственных чисел. Согласование направления собственных векторов и определение эмпирических главных компонент

-

вычисление эмпирических значений собственных чисел как среднего зна-

1T t чения собственных чисел для различных выборок λ =   ∑ λ ;

^{i T} t =1 ⁱ

• -    согласование направлений собственных векторов (главных компонент) для разных наблюдений:

Рассматриваем по числу переменных n вариантов выбора направления главных компонент с номером i (ГК i ). Для k-го варианта максимизируем вычисляемое отношение сиг-нал/шум у k-ой переменной SNR ij ( k ) — отношение среднего значения факторных нагрузок к среднеквадратичному отклонению этих величин для всех наблюдений:

m- ( k )

SNR, (k)) =   ---, ij         Si j ()) ’

1 T t где mij (k) = ~ Е w ij (k) — средние значения нагрузок в наборе из T i-ых главных T t=1

T компонент для

ное отклонение

Максимальное

k-го варианта, s ² = _ £ ( w t_tj ( k ) - m ( k )) ² — среднеквадратич- T t=1

значения нагрузок для k-го варианта; i, j , k = 1,…,n.

значение вычисляемого отношения сигнал/шум у k-ой переменной

SNR ij ( к ) достигается, если все нагрузки k-ой переменной имеют одинаковые знаки.

Нагрузки, для которых вычисленное значение отношения сигнал/шум SNRij (к) не менее порогового значения

SNRij (k) ^ SNRthr., считаем значимыми, а переменные с такой нагрузкой действующими. Сумму вычисленных значений отношения сигнал/шум у действующих переменных для варианта k запоминаем:

S i i ( k ) = E SNR ij ( k ) ,

j где j — номер действующей переменной для k-го варианта выбора направления ГКi.

Из n рассмотренных вариантов выбора направлений выбирается вариант k*, для которого сумма отношений сигнал/шум у действующих переменных максимальна

k * : S 1 i ( k *) = max S 1 i ( k ) , S i i = S i i ( k * ) .

k

• -    определение эмпирических главных компонент w _i = w _{i 1} , w _{i 2} , w _in , i = 1, …, n: факторные нагрузки у недействующих переменных обнуляются, для действующих переменных в качестве значения факторной нагрузки принимаем

среднее значение по всем наблюдениям (при согласовании направлений собственных векторов):

I T t ,*..

w ij = ~ 2 wij ( k ) ;

T t = 1

• -    выбор числа эмпирических главных компонент (ЭГК) N ( N ≤ n ).

Количество выбранных ЭГК N должно обеспечивать максимально возможную информативность вычисляемой интегральной характеристики γ :

Y = Y, • Ysnr где

^Y SNR =

S 11 + S 12 + ... + S 1N

S 21 + S 22 + ... + S 2 N

—SNR-информативность,

= ^X 1 + X 2 + ... + X n

— дисперсионная информативность.

^Y °    X 1 + X 2 + ... + X _n

4 шаг. Согласование направлений эмпирических главных компонент нормирование ЭГК умножением на квадратный корень из соответствую- щего эмпирического собственного числа:

* \

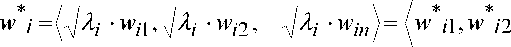
w in

;

согласование направлений нормированных ЭГК.

Критерием выбора направления ЭГК является максимизация значений целевой функции, вычисляемое как свертка значений данных на компоненты вектора весов. Максимальное значение неотрицательных переменных есть единица, поэтому для максимизации значений целевой функции выбираем из двух возможных направлений эмпирической главной компоненты то, при котором сумма ее координат максимальна;

• -    нахождение единого для всех наблюдений вектора весовых коэффициентов W * = W**, , _w* 2 , ..., w* ni суммированием нагрузок согласованных эмпириче-

• * N*

ских главных компонент w j — ^ W j , j = 1,^,n, i = 1,^,N.

i=1

• -    вычисление интегрального показателя для наблюдения t как суммы про- ^t

изведений значений вектора весов и матрицы унифицированных показателей A qt = At-W*.                                        (5)

Для фиксированного момента t интегральную оценку для объекта c номером i записывают в виде аддитивной свертки данных с весами, определяемыми вектором W*:

n qt = Ewj ■ aij , i = 1, -> m, j = 1, -> n.       (6)

j =1

• 5    шаг. Определение весовых коэффициентов блоков

• - вес блока l w^~ _l , где l = 1,…, L , ( L — количество блоков) пропорционален

величине суммы действующих ОСШ этого блока S ₁ ^l :

l              L                                N _l

W i =        -----_T, E w = 1, w ^ 0 , S 1 = E S li ,

S1 + S12 +...+S1L l=1                               i=i где Nl — число выбранных эмпирических главных компонент в блоке l.

• 6    шаг. Вычисление интегральной характеристики системы

  - вычисляем характеристику всей системы, учитывая веса блоков:

4.    Вычисление интегральных индикаторов качества жизнинаселения с помощью предложенного алгоритма

L tt yit = ∑ w~l ⋅qitl⋅ , l=1

t

где q il — интегральная оценка блока l для объекта c номером i в момент t.

Шаги 2,3,4 и 5 выполняются независимо для каждого блока. На шаге 6 используются результаты предыдущих шагов.

Рассмотрим работу алгоритма для вычисления интегральной характеристики качества жизни населения субъектов Российской Федерации. Выбор переменных и деление их на блоки является принципиальным вопросом, лежащим вне рассматриваемого обсуждения. Поэтому воспользуемся списком переменных из исследования, выполненного под руководством С.А. Айвазяна (табл.1), являющегося признанным авторитетом в исследовании качества жизни [7]. Деление переменных на блоки также произведено авторами исследования [7]. Отсутствующие в открытом доступе данные заменим на близкие к ним (выделено цветом в табл.1). Все значения переменных взяты из открытых справочников Росстата [12].

Вменение отсутствующих значений является уязвимым местом методик вычисления интегральной характеристики. Наличие ряда наблюдений во многом снимает эту проблему. Единичные отсутствующие значения восстановлены линейной интерполяцией по соседним имеющимся, в случае отсутствия значений показателей для ряда лет их дополняем их средними значениями по тому федеральному округу, к которому относится рассматриваемый субъект Федерации.

Среди перечисленных переменных переменные 1, 2, 5, 7, 9, 10, 12, 21, 22, 23 связаны с вычисляемой характеристикой монотонной возрастающей зависимостью, когда оптимальное значение j - го показателя максимально. Для остальных показателей, кроме переменной 27, оптимальное значение показателя минимально. Для переменной 27 «Коэффициент миграционного прироста» примем x j^opt = 0, j=27. Значение соответствует ситуации, когда количество выбывших из региона совпадает с количеством приехавших.

Определение четвертой эмпирической главной компоненты представлено в табл.2 Выбранные направления собственных векторов максимизируют сумму значений ОСШ у действующих переменных, для которых отношение сигнал/шум — отношение среднего к среднеквадратичному отклонению — не менее 2,2. В этой ЭГК оказалась одна действующая переменная (выделена темным цветом в табл.2). Факторные нагрузки этой переменной в ЭГК определит средняя величина нагрузки по годам, остальные переменные в ЭГК обнуляются (так же, как в методах факторного анализа).

Таблица 1

Переменные для вычисления интегральных индикаторов качества жизни населения

Уровень благосостояния населения
1	Отношение ВРП на душу населения к прожиточному мин, единиц
2	Покупательская способность среднедушевых денежных доходов по отношению к наборам прожиточного минимума (%)
3	Доля численности населения с денежными доходами ниже прожиточного минимума (%)
4	Отношение совокупных доходов 20% самых богатых и 20% самых бедных
5	Обеспеченность населения собственными легковыми автомобилями (автомобилей/1 000 чел.)
6	Доля семей, состоящих на учете на получение жилья (%)
7	Приходится общей площади жилищного фонда на одного жителя (кв. м/10 чел.)
8	Доля ветхого и аварийного жилья (%)
9	Плотность автомобильных дорог общего пользования (км/10 000 кв. км)
Качество населения
10	Ожидаемая продолжительность жизни при рождении (лет)
11	Число умерших детей в возрасте до 1 года на 1000 населения (чел.)
12	Коэффициент естественного прироста (на 1000 населения)
13	Число умерших от инфекционных и паразитарных болезней и туберкулеза на 100 000 нас.
14	Число умерших от новообразований на 100 000 населения (чел.)
15	Число умерших от болезней системы кровообращения на 100 000 населения (чел.)
16	Число умерших от болезней органов дыхания на 100 000 населения (чел.)
17	Число умерших от болезней органов пищеварения на 100 000 населения (чел.)
18	Заболеваемость от травм, отравлений и некоторых других внешних причин на 100 000 нас.
19	Число инвалидов на 1 000 населения (чел.)
20	Зарегистрировано случаев заболевания врожденными аномалиями на 1 000 населения
21	Доля специалистов с высшим образованием среди занятых в экономике (%)
22	Приведенная производительность труда (ВРП/среднегодовая численность занятых в экономике, тыс. руб./чел.)
23	Количество выпускников высших и средних учебных заведений на 1000 населения
Качество социальной сферы
24	Уровень безработицы (%)
25	Доля работников занятых во вредных и опасных условиях труда в среднегодовой численности занятых в экономике (%)
26	Численность пострадавших на производстве со смертельным исходом или с утратой трудоспособности на 1 рабочий день и более на 1 000 работающих
27	Коэффициент миграционного прироста на 10 000 населения
28	Число зарегистрированных умышленных убийств и покушений на убийство на 100 000 нас.
29	Число зарегистрир. фактов умышл. причинения тяжкого вреда здоровью на 100 000 нас.
30	Число зарегистрированных изнасилований и покушений на изнасилование на 100 000 нас.
31	Число разбоев, грабежей, краж из квартир граждан в расчете на 100 000 населения
32	Число зарегистрированных незаконных присвоений или растрат в расчете на 100 000 нас.
33	Число больных, состоящих на учете с диагнозом наркомания и токсикомания на 100 000 нас.
34	Число больных, состоящих на учете с диагнозом алкоголизм в расчете на 100 000 нас.
35	Число больных, инфицированных туберкулезом в расчете на 100 000 населения
36	Смертность от внешних причин на 100 000 населения
37	Число больных психическими расстройствами на 100 000 населения

Таблица 2

Определение четвертой эмпирической главной компоненты Блока 1

4 ГК	Переменные
	1	2	3	4	5	6	7	8	9
2007	0,21	–0,23	–0,31	–0,09	0,42	0,46	–0,14	0,04	–0,62
2008	0,08	–0,07	–0,44	–0,35	0,37	0,32	–0,56	0,31	–0,16
2009	–0,06	0,04	–0,36	–0,43	0,18	0,39	–0,64	0,30	0,03
2010	–0,01	–0,04	–0,42	–0,40	0,31	0,18	–0,60	0,40	0,12
2011	–0,10	–0,02	–0,40	–0,41	0,27	–0,07	–0,47	0,60	0,07
2012	–0,03	–0,04	–0,37	–0,34	0,22	–0,30	–0,29	0,72	0,02
2013	0,02	0,00	–0,20	–0,05	–0,03	–0,69	0,24	0,63	–0,20
2014	–0,06	–0,04	–0,28	–0,26	–0,37	0,27	–0,29	0,72	–0,20
Среднее, m	0,01	–0,05	–0,35	–0,29	0,17	0,07	–0,34	0,46	–0,12
Выб. ср.квадр.откл., s	0,10	0,08	0,08	0,15	0,26	0,40	0,29	0,24	0,24
ОСШ	0,07	0,62	4,26	1,97	0,67	0,18	1,17	1,92	0,49
	Сумма ОСШ по строке								11,34
	Действующие ОСШ								4,26

В табл.3 представлены все нормализованные и согласованные по направлению эмпирические главные компоненты (ЭГК) первого блока. Поскольку четвертое собственное число Я 4 = 0,79 <  1 , значения факторной нагрузки в этой ЭГК уменьшились по сравнению с табл.2. Направления ЭГК выбираются, чтобы максимизировать значение вычисляемой линейной свертки определяемых весов (как правило, положительных) с переменными, чьи значения лежат на интервале [0, 1].

Эмпирические главные компоненты Блока 1

Таблица 3

№ ГК	Эмпирические собственные числа	Переменные
		1	2	3	4	5	6	7	8	9
1	3,34	0,80	0,90	0,82	–0,75	0,53		0,38	0,31
2	2,04	–0,27	–0,31		0,43	0,43	0,64	0,64	0,64
3	1,14		0,19			–0,37			0,18	0,79
4	0,79			0,31
5	0,61								0,34
6	0,50					0,43			–0,26
7	0,31	0,35	–0,12	–0,24						0,19
8	0,24				0,26			–0,20	0,12
9	0,03		0,14	–0,08	0,08
Вектор весов		0,88	0,79	0,81	0,02	1,02	0,64	0,83	1,33	0,98

Максимальное значение, вносимое ЭГК в композитный индекс, достигается, если все значения переменных равны единице, т.е. определяется суммированием факторных нагрузок ЭГК. Если сумма факторных нагрузок у ЭГК отрицательна, значение направление меняем. Так четвертая ЭГК, определяемая табл.2, изменила направление.

Искомый вектор весов определяется суммированием одноименных переменных выбранного числа эмпирических главных компонент, представленных в табл.3. Число та- ких компонент выбирается, чтобы максимизировать информативность полученного решения согласно (4).

Определение информативности интегрального показателя Блока 1.

Уровень благосостояния населения

Таблица 4

	Номер эмпирической главной компоненты
	1	2	3	4	5	6	7	8	9
Сумма ОСШ k – ой ЭГК	102,2	57,6	19,7	11,3	7,9	10,7	20,9	16,5	100,5
Сумма действующих ОСШ k – ой ЭГК	101,4	55,0	15,4	4,2	3,4	4,9	16,5	10,8	95,7
Накопленный вклад, γ SNR	0,99	0,98	0,96	0,92	0,90	0,88	0,87	0,86	0,88
Эмпирические собственные числа	3,34	2,04	1,14	0,79	0,61	0,50	0,31	0,24	0,03
Накопленный вклад, γ σ	0,37	0,60	0,72	0,81	0,88	0,94	0,97	1,00	1,00
Информативность, γ σ ⋅ γ SNR	0,37	0,58	0,69	0,75	0,79	0,82	0,85	0,85	0,88

В табл.4 приведен пример определения информативности интегрального показателя Блока 1 «Уровень благосостояния населения». При рассмотрении всех 9 ЭГК суммарная информативность максимальна и составит около 88%. Поэтому для вычисления интегрального показателя используем все эмпирические главные компоненты. Чем больше переменных описывают систему, тем меньшее их относительное количество участвует в построении композитного индекса. Для второго блока выбираем 11 из 14 ЭГК, для третьего — 10 из 14 ЭГК. (В другом случае в системе, которую описывают 51 переменных, было выбрано 21 ЭГК). Веса блоков определяем пропорционально действующим ОСШ переменных этого блока (табл.5), что аналогично пропорциональности силе принятого сигнала. Блок 3 «Качество социальной сферы», в котором 14 переменных, оказался менее значим, чем блок 1 «Уровень благосостояния населения», в котором 9 переменных.

Таблица 5

Определение весов блоков

Блок	1	2	3
Сумма действующих ОСШ	307,4	397,7	254,3
Вес блока	0,32	0,41	0,27

Основной недостаток методик определения весов с помощью аппарата факторного анализа состоит в необоснованных резких изменениях рейтингов объектов для последовательных наблюдений. При рассмотрении коротких временных промежутков при отсутствии катастроф и потрясений естественно ожидать плавное изменение как регистрируемых показателей, так и интегрального показателя качества системы и рейтингов, выставляемых на основании этого показателя. Отсутствие резких колебаний является естественным следствием предположения об адекватности рассматриваемой модели объективной реальности.

В проведенном исследовании число объектов, где значения рейтинга изменились по сравнению с предыдущим годом более чем на 15% от возможного максимального изменения, составило 1,1% случаев. Для сравнения, в работах [3, 4], где вычислялись интегральные характеристики муниципальных образований Тюменской и Самарской области для ряда лет, эта величина составляет 42,7% и 43,2%. Среднее изменение рейтинга за год в этих исследованиях составляет около 20%, в приведенном исследовании — 3,7%. Приведенную в [3, 4] интегральную характеристику нельзя назвать надежной, и на её основе оценивать качество жизни субъектов РФ. Источником неудовлетворительного качества вычисленных характеристик может являться, в частности, погрешность исходных данных, которую не учитывает классический метол главных компонент. Отметим, что ранги 25 развитых европейских стран за 2009–2011 годы, выставленные на основании значений ИРПЧ, дают среднее изменение рейтинга за год 7,7% [18].

На рис.2 показаны изменения интегральной характеристики качества жизни для Уральского ФО. Ожидаемо северные субъекты округа, ориентированные на добычу нефти и газа, имеют более высокие показатели качества жизни, чем промышленные области. За 100% принято максимальное значение интегральной характеристики в 2007 году (Москва), за 0% — минимальное значение в 2007 году (Тыва).

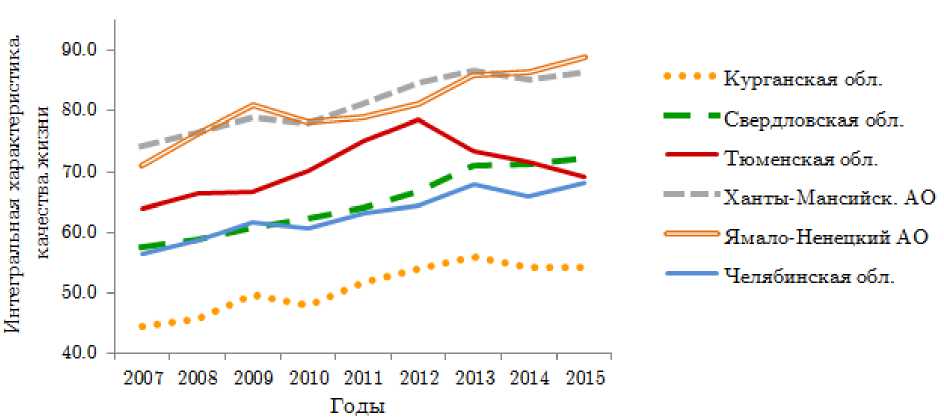
Рис. 2 . Интегральная характеристика качества жизни некоторых субъектов

Российской Федерации за 2007–2014 годы (2015 год — прогноз)

Заключение

В работе рассмотрено решение задачи построения латентной интегральной характеристики изменения качества системы на основании регистрируемых измерений для ряда наблюдений. Задача относится к классу задач выделения полезного сигнала из массива данных в условиях априорной неопределенности и решается на основании задаваемого отношения сигнал/шум. Предложен алгоритм построения интегральных характеристик с определением неслучайных составляющих главных компонент, характеризующих структуру рассматриваемой системы. Также предложен новый подход к выбору числа главных компонент, к определению весов рассматриваемых подсистем и к определению информативности полученной характеристики на основании дисперсионного критерия и выбранного параметра — отношения сигнал/шум. Алгоритм был использован для получения интегральных индикаторов качества жизни населения субъектов Российской Фе- дерации. Предлагаемая методика может быть использована для вычисления интегральных оценок изменения качества плохо формализуемых систем. В дальнейшем следует проанализировать результаты применения методики построения интегральной характеристики качества системы не для заведомо хорошего (и не очень большого) набора входных переменных, а используя широкую базу измерений разных социальных систем, фиксируемую Росстатом.

Работа выполнена при финансовой поддержке проектной части государственного задания в сфере научной активности Министерства образования и науки Российской Федерации, проект № 1.949.2014/K.