Алгоритм построения периферийного шнура фронтальной сети для трансформируемого сетчатого рефлектора космического аппарата

ОАО «Информационные спутниковые системы» имени академика М. Ф. Решетнева» активно занимается созданием крупногабаритных трансформируемых рефлекторов, используемых в качестве целевой аппаратуры на телекоммуникационных космических аппаратах. В настоящее время ведется разработка трансформируемого сетчатого рефлектора с апертурой диаметром до 40 м. В состав такого рефлектора входят следующие основные конструктивные элементы (рис. 1):

• -    силовой каркас, состоящий из основания, спиц и силовых шнуров;

• -    формообразующая структура (ФОС), обеспечивающая придание и поддержание заданной формы отражающей поверхности;

• -    отражающая поверхность (на рис. 1 не показана), представляющая собой растянутое сетеполотно и выполняющее функцию передачи электромагнитной волны между источником (приемником) сигнала и облучателем антенной системы.

Ранее, одним из авторов статьи [1] был проведен анализ вариантов исполнения ФОС трансформируемого сетчатого рефлектора. Выбранная по результатам данного анализа ФОС имеет в своем составе следующие конструктивные элементы:

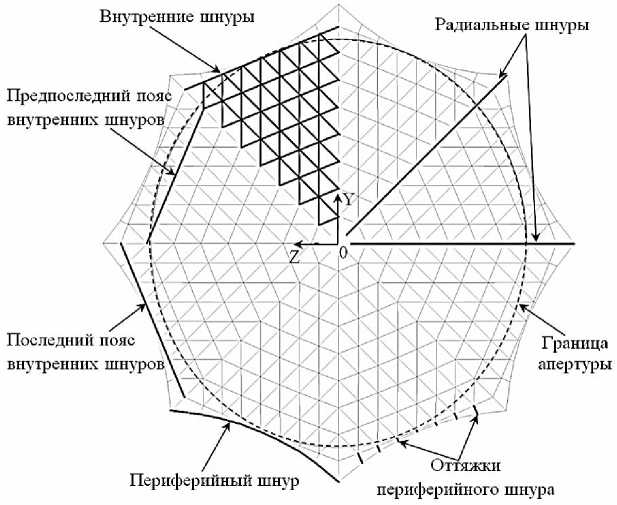
• -    фронтальная сеть (ФС) – система натянутых шнуров, в которую входят радиальные и внутренние шнуры, а также периферийный шнур и его оттяжки (рис. 2); формирует разбиение отражающей поверхности на фацеты, обеспечивая требуемую форму рабочей поверхности рефлектора;

• -    тыльная сеть (ТС) – система натянутых шнуров для поддержания фронтальной сети в заданном положении; имеет структуру, аналогичную фронтальной сети, симметрично отраженную относительно срединной плоскости основания рефлектора;

• -    вантовая система – конструктивный элемент формообразующей структуры, соединяющий каждый узел фронтальной сети с соответствующим узлом тыльной сети.

Натяжение внутренних шнуров ФС обеспечивается растяжением периферийного шнура (ПШ). ПШ должен иметь геометрическую форму и усилие натяжения, обеспечивающее равномерное натяжение всех внутренних шнуров ФС. Максимальная величина прогиба ПШ, с одной стороны, зависит от положения концов звеньев А (для ФС) или звеньев Б (для ТС) соседних спиц, с другой стороны, от границ апертуры рефлектора (рис. 2).

На этапе проектирования сетчатых рефлекторов с целью оценки усилий, возникающих в напряженной конструкции, ранее применялись методы построения периферийного шнура, которые вносили погрешность в определение равновесного напряженного состояния конечно-элементной модели ФОС. Использование приближенных методов при создании конечноэлементной модели рассматриваемого рефлектора обусловлено тем, что узлы фронтальной сети должны находиться на поверхности офсетной цилиндрической вырезки из параболоида вращения. Однако применение ряда допущений, упрощающих процесс расчета геометрической формы и усилий в ПШ, привели к появлению отрицательных значений усилий в некоторых зонах ФС. Это подтолкнуло авторов статьи к разработке наиболее подробного алгоритма построения периферийного шнура, учитывающего пространственное расположение натянутых шнуров.

Фронтальная (тыльная) сеть имеет n секторов (где n = 8 – количество спиц рефлектора) и образована фацетами треугольной формы, как показано на рис. 2. Треугольная форма фацет выбрана на основании анализа результатов расчета среднеквадратического отклонения формы отражающей поверхности рефлектора [1]. Количество фацет, расположенных вдоль радиального направления, m штук (в рассматриваемом рефлекторе m = 8).

Построение оттяжек периферийного шнура. Оттяжки периферийного шнура обеспечивают связь между внутренними шнурами ФС (ТС) и периферийным шнуром. Направление оттяжек периферийного шнура и величина натяжения в них определяется из условия обеспечения равенства натяжений во внутренних шнурах ФС (ТС). Дальнейшее описание построений ведется для фронтальной сети. Тыльная сеть строится аналогично.

В каждый узел ФС, расположенный на последнем поясе внутренних шнуров, входит по четыре шнура (рис. 3), образуя пространственную систему сходя щихся сил. Уравновешивающая реакция R со стороны оттяжки ПШ равна по модулю и обратна по направлению равнодействующей. Определим равнодействующую данной системы сил [2]. Ниже приведено более подробное описание построения на примере одной оттяжки ПШ.

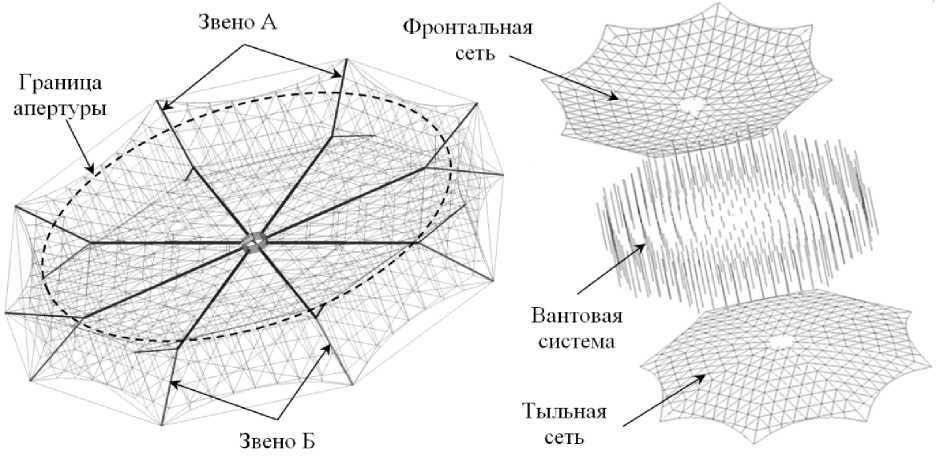
Рис. 1. Состав конструкции трансформируемого сетчатого рефлектора

Граница апертуры

Радиальные шнуры

Последний пояс у внутренних шнуров'

Периферийный шнур

Внутренние шнуры

Предпоследний пояс / внутренних шнуров /1-—

Оттяжки периферийного шнура

Рис. 2. Схема фронтальной (тыльной) сети

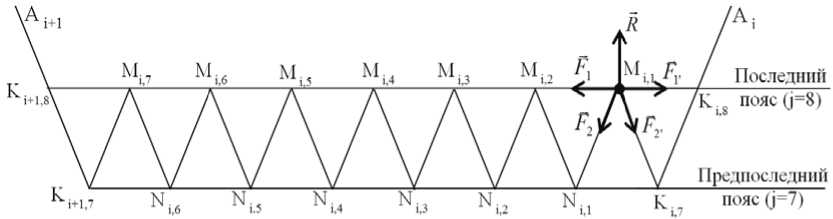
Рис. 3. Схема построения оттяжки периферийного шнура:

i – номер сектора (спицы); j = 1, …, m , где m = 8 – количество фацет вдоль радиального направления;

A _i – точки крепления ФС к силовому каркасу; K _i, j – узлы радиальных шнуров; M _i, ( _1…m-1 ) – узлы последнего пояса внутренних шнуров; N _i, ( _1…m-2 ) – узлы предпоследнего пояса внутренних шнуров;

F 1, F ₂ , F 1‘ , F 2‘ - векторы натяжений внутренних шнуров; R - вектор натяжения оттяжки ПШ

Шнур в натянутом состоянии представляет собой отрезок прямой. Как известно, уравнение прямой в пространстве, проходящей, к примеру, через две данные точки Mj (x^у^zx) и M2 (x2;у2;z2), имеет вид x - x,    у - у z - z,

----— =-----— =----—, или в каноническом виде x 2 - xi У 2 - У1 z 2 - z1

x - X 1 _ у - у 1 _ z - z 1

lmn где

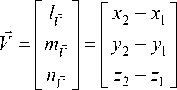
направляющий вектор.

Все вычисления ведутся в системе координат реф- лектора, где начало координат находится в центре рефлектора, оси Y и Z лежат в срединной плоскости рефлектора и направлены, как показано на рис. 2, ось X – достраивает систему координат до правой.

Определим орт направляющего вектора по формуле le v m- V . n-V

—* V I V I

Затем определим углы между ортом и осями X, Y и Z соответственно:

a = arccos ( l ^- V ) , P = arccos ( m ^- V ) , у = arccos ( n ^- V ) .

Зная величину усилия | F t | в шнуре и его направление в пространстве, найдем модуль проекций вектора на оси X, Y и Z соответственно:

^lFt = | F -|"^cos (^a) , ^mFt = | F — I"^cos ( P ) , n Ft = | F -|"^cos ( Y ) .

Определим координаты вектора R на оси X, Y и Z, суммируя проекции всех сил на каждую из осей:

Модуль вектора R есть величина усилия натяжения в оттяжке периферийного шнура; оттяжка лежит на прямой, параллельной орту e _R .

Построение периферийного шнура. Ниже пошагово описан алгоритм построения периферийного шнура, блок-схема которого представлена на рис. 4.

Отражающая поверхность и конструкция рефлектора обладают свойством симметрии относительно плоскости 0XY. Рассматриваемый рефлектор имеет 8 спиц, расположенных симметрично относительно плоскости 0XY, поэтому достаточно построить половину периферийного шнура, расположенную по одну сторону от плоскости симметрии.

Шаг 1 . В соответствии с блок-схемой, показанной на рис. 4, построение периферийного шнура ведется последовательно от сектора к сектору. Внутри каждого сектора построение ПШ начинается от точки крепления ПШ к спице силового каркаса A ( x_A ; у A ; z_A ) i . Конечная форма и распределение усилий в участках ПШ зависят от двух параметров, задаваемых в начале работы алгоритма:

• -    ( 1 0 ) i - длина первой оттяжки ПШ в секторе i ;

• -    T_i1 - величина натяжения первой в секторе i оттяжки ПШ.

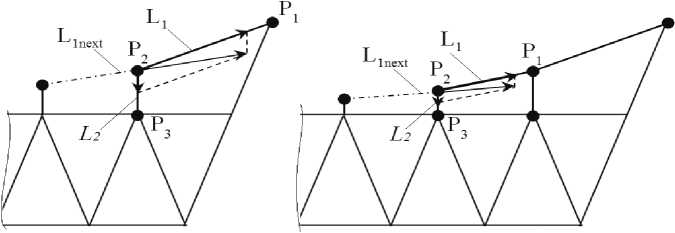
Шаг 2 , 3 . Дальнейшее выполнение алгоритма заключается в работе цикла построения ПШ по секторам (шаг 2) и вложенного в него цикла построения ПШ по участкам внутри секторов (шаг 3). Построение ПШ разбивается на несколько шагов в зависимости от количества секторов (спиц) и количества фацет, расположенных вдоль радиальных шнуров. На каждом шаге выбираются три точки (рис. 5):

——

R =

m R . ⁿR

^lF1 ^{+ l}F 2 ^{+ l}F1' ^{+ l}F 2' ^mF1 ^{+ m}F 2 ^{+ m} F 1' ^{+ m}F 2' ⁿF1 ^{+ n}F 2 ^{+ n}F ^— 1' ^{+ n}F 2'

■ -R

——

, e R = ^{m -} R

n - R

—— R I R I

x ₁

x ₂

( P 1 \j = у 1

( P 2 ) _1А = у 2     , ( P 3 ) j

z->

² i , j

x ₃

y ₃

z ₃

. (2)

i , j

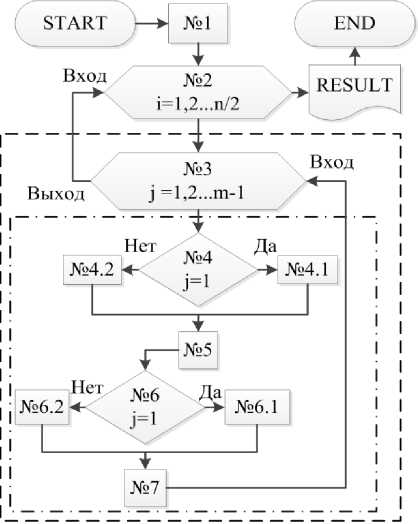
Рис. 4. Блок-схема алгоритма построения периферийного шнура:

i – номер сектора (или спицы); j – номер участка ПШ;

n – количество секторов (спиц); m – количество фацет вдоль радиального направления

а                                     б

Рис. 5. Схема построения участка периферийного шнура в первом секторе

Шаг 4 . Шаг 4.1. выполняется в случае построения первого участка ПШ ( j = 1) в рассматриваемом секторе, как показано на рис. 5, а :

x ₂

( P 1 ) , ,1

x 1

У 1 - ^z i 1,1

xf yf

- zf J i

( P 3 ) i ,1

x 3

У з - z 3 1 ,1

xM yM

- zM .Ц

,

( P 2 ) , ,1

" 2

У i z?

2 ,1

= (eRX, •(t0 X +

x ³

У 3

^{z 3} 1 ,1

Иначе выполняется шаг 4.2 ( j >  1), как показано на рис. 5, б :

	x 1		x 2		x 3	xlast _ 1
( P 1 ) i , j =	У 1 - z 1 .	= i , j	У 2 - Z 2 .	, ( P 3 У = i , j - 1	У 3    = z3 3 i , j	y last _1 - z last _1 J	i , j

( Pi Xj

У 2     = ( e R ) , , j s 0 ⁺

'2 1'J

x 3

y 3

z3 . .

³ , j

leLR1 •( У3 - У1) i, j - meLR1 '( x3 - x1) i,j где s0 =---------—-------------—. Коэффи- m—LR 1 • leR - leLR 1 • meR циенты leLR 1, mgLR 1, ngLR 1 определяются по фор-

муле (12).

Шаг 5 . Орт e_{L 2} = ( e_R ) , j направляющего вектора

прямой L 2 , на которой лежит оттяжка ПШ, найден ранее по формуле (1). Далее определяем орт e_L 1 направляющего вектора прямой L 1 , на которой лежит участок ПШ:

—*

L1 =

^lL1 ^m L 1 n £1 .

x 1 ^- x 2

У 1 ^- У 2

z ₁

-

z ₂

i , j

^—

— eL = 7?"T

Определим угол между участком ПШ и оттяжкой ПШ по формуле Z i j = arccos ( e_L 1 • e_{L 2} ) .

Далее по правилу параллелограмма найдем модуль равнодействующей системы сил, действующих на точку ( ^P2 ) , j ^[2].

Шаг 6 . Шаг 6.1. выполняется в случае построения первого участка ПШ в секторе, как показано на рис. 5, а :

1/2

T ,j + 1 = T ,2 = ( R i ,1² + T ,1² + 2 • Bn • T ,1 • cos ( Z i ,1 ) ) .(6)

Иначе выполняется шаг 6.2 ( j >  1), как показано на рис 5, б :

T i j = T ij (см. формулу (13)),

1/2

T ,j + 1 = ( R i,j + T j + 2 • R j • T ,j • cos ( C i , y ) )    . (7)

Полученная величина T i,j+1 есть усилие натяжения в следующем участке ПШ.

Шаг 7 . Теперь необходимо определить направление следующего участка ПШ. Для этого определим направляющий вектор следующего участка ПШ, а также его орт:

^—

L next =

l [1 next mH next

ⁿ — 1 next

= ^eL1 ' ^Ti , j ^{+ e}L 2 * R i , j

—      _ Li next   /o\ eL 1 next    | — I . (8)

L 1 next

Рассмотрим три вектора: e_L 1 next — орт направляющего вектора следующего участка ПШ; ( e_R ) . j + 1 - орт направляющего вектора следующей оттяжки ПШ,

Г l—— 1 Vc ( x2 )i,j -(x з )i,j+1 —* Vc = mVc = ( У2 )i,j -(У з) i, j+1 – направляющий век- _ П!?с _ _( z2 )i,j -(z з )i,j+1 _ где Pguy тор прямой, проходящей через точки (P2) и (P3) . j+1. Найдем смешанное произведение этих век

торов: (eL1 next, (eR )i,j+1, Vc )* 0. Смешанное произве- дение не равно нулю. Следовательно, прямые являются скрещивающимися, т. е. соседние участки ПШ не лежат в одной плоскости [3].

Для того чтобы определить координаты точки (P2)i j+1, необходимо разложить реакцию со стороны следующего участка ПШ RL1 next = Tj+1 ‘ eL1 next на две составляющие.

Первая компонента R 1 L 1 next лежит на прямой, полученной пересечением плоскостей Plane 1 и Plane 2 . Plane 1 задается прямой следующей оттяжки ПШ и точкой ( P ₂ ) . Plane ₂ задается вектором L 1 _next и точкой P _guy на ванте ФОС, соединяющей узел ФС ( P ₂ ) . . с соответствующим узлом ТС. Вторая компонента

R 2 L 1 next направлена вдоль рассматриваемой ванты ФОС.

Плоскости Plane 1 и Plane 2 описываются уравнениями:

A plane 1 • ^{x +} B plane 1 • y ^{+ C}plane 1 • z ⁺ D plane 1 ⁰

и

A plane 2 • x ⁺ B plane 2 • y ^{+ C}plane 2 • z ⁺ D plane 2 = ⁰ .    ⁽⁹⁾

Найдем коэффициенты при уравнениях плоскости Plane 1 :

Aplane1 = ((yM )i,j+1 — (y2 )i,j ) X x (n—R L+1 - ((zM L+1 - (z 2 L) •(meR )i,j+1,

B plane 1 = ^{( ( Z}M ) i , j + 1 ^{- ( Z} 2 ) i , j ) ^X

^{X( l} e R L+1 — ( ⁽ x M L+1 — ⁽ x 2 L)< n e R L+P

^Cplane 1 = ^{( (} x M ) i j + 1 ^{— (} x 2 ) , j ) ^X

,            ,                          (10)

^{x (} m eR L+ 1 ^- ( ⁽ У м L+ 1 — ^{( y} 2 ) i , j ) • ^{( l}eR L+ 1

и Plane 2 :

A plane 2 = ( ⁽ y 2 ) i , j y gpty ) " n e R ( ^{( Z} 2 ) i , j z guy ) " m e R ,

B plane 2 = ( ^{( Z} 2 ) i , j z guy ) • ^leR ( ⁽ x 2 ) i , j x guy ) • ⁿ e R ,

^Cplane 2    ( ^{( x} 2 ) i , j x guy ) • m e R   ( ⁽ y 2 ) i , j    y ppiy ) • ^le R ,    ⁽¹¹⁾

x guy y guy z guy

— ⁽ x 2 ) , , j ⁽ У 2 ) - , j ⁽ z 2 ) - , j

– точка, принадлежащая

прямой, на которой лежит ванта, соединяющая соответствующие узлы фронтальной и тыльной сетей. Данная ванта ориентирована параллельно оси X в системе координат рефлектора.

Определим направление вектора участка ПШ через уравнение прямой, образованной пересечением плоскостей Plane ₁ и Plane ₂ [3]:

Г i — 1 LR1 Bplane 1 Cpl^ane 2   Cpil^ane 1 Bp>lane 2 —— LR1 = mLR1 = C plane 1 Aplane 2   Aplane 1 Cplane 2 _ ntR1 _ _ Aplane 1 Bplane2  Bplane1 Aplane 2 _ eLR 1 = leLR1

m e LR 1

ⁿ e LR 1

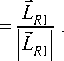
Найдем угол между вектором RL1next и его компонентой R1L1 next по формуле cos (ф1 ) = eL 1 next • eLR 1, а затем определим величину натяжения T'i j+1 в сле- дующем участке ПШ, лежащим на прямой с направляющим вектором R1L1next :

T R 1 = Ti,j + 1 ' c^os( V 1 ), T i , j + 1 = T R 1 -          ⁽¹³⁾

Далее найдем угол между векторами R 1 L 1 next и R 2 L 1 next по формуле cos ( ф ₂ ) = l e_LR ! [3].

Составим квадратное уравнение по правилу параллелограмма относительно T_{R 2} :

( Tj+ 1 ) 2 = ( T r 1 ) ² + ( T r 2 ) ² + 2 ■ ( T r 1 ) ■ ( T r 2 ) ■ cos ( Ф 2 ) (14)

и, решив его для положительного значения T R 2 , найдем величину натяжения в ванте:

_{2                     2} 1/2

T R 2 =^{- T}R1 ■ ^{cos (}9 2 ^{) +} (^{( T}R1 ■ ^{cos (}Ф 2 ) ) - ^TR1 ⁺ ( ^Ti , j + 1 ) ) .⁽¹⁵⁾

После выполнения шага 7 следует переход на новый круг (если j < m – 1, то j = j + 1; если j = m – 1, то i = i + 1 и j = 1).

В конце работы алгоритма на выходе получаем массивы данных:

• -    [ P 2 ] — координаты узлов периферийного шнура;

• -    [ T ] - величины натяжений в участках периферийного шнура.

В результате построения получим геометрическое место узлов периферийного шнура, а также величины натяжений в каждом участке периферийного шнура.

Данный алгоритм был использован при написании макросов на процедурном языке APDL конечноэлементного комплекса ANSYS. Построенная конечно-элементная модель фронтальной сети рассматриваемого сетчатого рефлектора получила предварительное натяжение в соответствии с заданными и расчетными требованиями. Затем был проведен поиск равновесного состояния, в результате которого путем варьирования параметров была получена напряженная модель фронтальной сети, оптимизированная с необходимой точностью усилий натяжения в шнурах.

Применение разработанного авторами статьи алгоритма позволяет с использованием простых методов оптимизации (например метод Хука–Дживса) получить конечные величины усилий в шнурах формообразующей структуры рефлектора. Рассмотрение алгоритма оптимизации построения периферийного шнура будет проведено в следующих работах авторов.