Алгоритм построения вогнутой оболочки множества точек

Построение вогнутой оболочки для множества точек плоскости в виде простого невыпуклого многоугольника, ограничивающего точки множества, имеет широкое применение: в компьютерной графике, распознавании образов, геоинформатике (ГИС) [1]. В отличие от построения минимальной выпуклой оболочки эта задача не имеет единственного решения. То есть не существует единственного варианта построения невыпуклой оболочки. По этой причине среди публикаций по теме построения невыпуклых оболочек множества точек нет работ, содержащих наилучший алгоритм, решающий данную задачу.

По критерию вычислительной сложности лучшим является алгоритм формирования вогнутой оболочки, представленный в статье [1]. Основан на триангуляции исходного множества точек, и дальнейшем последовательном исключении из нее самой длинной внешней стороны. Вычислительная сложность данного алгоритма оценивается как O ( n log n ). Недостаток этого и других подобных алгоритмов состоит в том, что добавление новых точек НВО определяется лишь триангуляцией, что приводит к высокой зазубренности формируемого многоугольника.

Другой тип алгоритмов формирования вогнутой оболочки основан на первоначальном построении минимальной выпуклой оболочки, на сторонах которой затем из оставшихся точек множества строятся впадины. К числу таких алгоритмов относится алгоритм Пака (Park J.S.), изложенный в [2], а также алгоритм Соловьевой А.Н. [3]. Недостатком этих алгоритмов является либо отсутствие критериев выбора новых точек для включения в НВО, либо применение сложных критериев, ограничивающих детализацию НВО.

Здесь рассматривается новый алгоритм построения вогнутой оболочки, также основанный первоначальном построении минимальной выпуклой оболочки, отличающийся тем, что в отборе точек для построения впадин используется оригинальный критерий, позволяющий сочетать достижение высокой детальности вогнутой оболочки с достаточной ее гладкостью.

Входными данными алгоритма служат множество P точек на плоскости и коэффициент детализации γ , задающий степень глубины впадин. Результат работы алгоритма – упорядоченное множество H вершин вогнутой оболочки.

Алгоритм выполняется в два этапа. На первом этапе находятся список H вершин минимальной выпуклой оболочки множества P (рис. 1а).

Вторым этапом алгоритма является цикл, в начале которого в списке H находится индекс m точки H[m] – начала стороны H[m] H[m+1] наибольшей длины, и по отношению к этой стороне во множе- стве G = P\H выполняется выбор дополнительной вершины pt, образующей впадину (рис. 1б). Зона выбора ограничивается рядом оригинальных условий. Если они выполняются, то pt добавляется в список H после точки H[m] в качестве новой вершины НМО. Если в G для стороны H[m] H[m +1] не находится точки, удовлетворяющей условиям выбора, то цикл завершается.

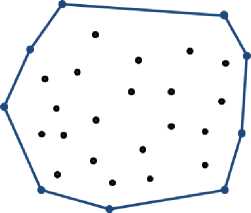
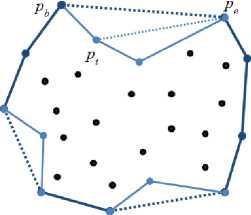
а )                                                        б )

Рис. 1. Этапы построения вогнутой оболочки

Обозначим начальную точку стороны H[m ] Hm +1] как р ь = H[m ] , а конечную -как p e = Hm +1].

В данном алгоритме зона выбора вершины pt ограничивается условием d 12 + d22 - dо2 < Y min(d 12, d22), где dо - длина рьре; d 1 - расстояние между рь и pt; d2 - расстояние между pe и pt; y - коэффициент детализации, определяющий границы зоны выбора.

Это условие ограничивает зону выбора в зависимости от значения у (рис.2). Так при y = 0 зона ограничена полукругом с центром в середине отрезка pbpe и диамет- ром, равным d0. При 0 < y < 2 зона ограничивается двумя дугами окружности диаметром большим d0. При y = 2 эти окружности вырождаются в параллельные прямые, а зона, соответственно, вырождается в бесконечную полосу шириной d0. При у > 2 зона так же ограничивается двумя дугами окружностей, но при этом с удалением от стороны pbpe зона расширяется.

Таким образом, значение y задает степень возможной глубины формируемых впадин вогнутой оболочки. Чем выше y , тем она больше и тем выше становится степень детальности вогнутой оболочки.

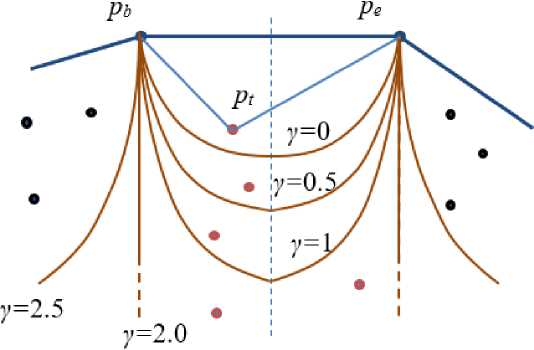
Рис. 2. Ограничение зоны поиска

Кроме выполнения условия нахождения в зоне выбора точка pt должна быть такой, чтобы стороны pbpt и pept треугольника pbpept не пересекались ни с одной из сторон вогнутой оболочки, построенных к этому моменту.

Из вех точек, удовлетворяющих этим условиям, выбирается та, которая со стороной pbpe образует треугольник pbpept с наименьшей площадью. Это гарантирует, что внутри треугольник pbpept нет другой точки из G, так как в ином случае она была бы вершиной pt треугольника наименьшей площади.

Если найдена точка pt, отвечающая всем перечисленным условиям, то она добавляется в список H между H[m] и H[m +1] и цикл повторяется. Иначе цикл завершается и завершается построение вогнутой оболочки.

Алгоритм построения вогнутой оболочки для множества точек на плоскости представлен ниже.

H = ConvexHull ( P ); // Список вершин минимальной выпуклой оболочки nh = H.Count ();

G = P\H ;

while ( true )

{                                                                        ~                              ~ m = IndexMaxSide(H); // индекс в H начальной точки наибольшей стороны pb = H[m];pe = H[(m + 1) % H.Count()];

jpt = -1;

qd 0 = qDist(pb, pe ); // квадрат расстояния pb, pe

Smin = 4 *qd 0;

foreach (pt in G )

{ qd 1 = qDist(pb, pt); qd2 = qDist(pe, pt);

if ( qd 1 + qd 2 - qd 0 >  y * Min ( qd 1 , qd 2)) continue ; //pt вне зоны выбора

St = Sq(pb, pt, pe );   // площадь треугольника pb, pt, pe );

if ( St < Smin )

{ if (IsCrossHull(pb, pt, ref H)) continue;

jpt = G.IndexOfpt );

Smin = St ;

}

} if (jpt > 0)

{

H.Insert ( m + 1 , G[jpt ]);

G.RemoveAt (jpt );

} else break;

}

Функция ConvexHull выделяет из множества P список вершин H минимальной выпуклой оболочки в качестве начального значения вогнутой оболочки. Функция ConvexHull возвращает список H , упорядоченный в соответствии с обходом по часовой стрелке.

В циклической части функцией IndexMaxSide в H находится индекс m начальной точки pb = H[m ] стороны наибольшей длины. Конечная ее точка pe = H(m + 1) % H.Count()]. Далее в зоне, определяемой условием отбора из G = P\H отбирается точка pt, наименее удаленная от pbpe. Мерой расстояния pt от pbpe служит площадь St треугольника pbpept. Функция IsCrossHull дополнительно исключает из отбора точку pt, если сторона pbpt или pept пересекается с какой-либо стороной текущего списка Н.

Если в G находится точка, удовлетворяющая всем условиям отбора, то она добавляется в список Н после H [ m ] и вычитается из G . Тогда в следующей итерации для поиска самой длинной стороны рассматривается расширенный список Н . Если же ни одна точка не соответствует условиям отбора, то цикл завершается.

Для проверки работоспособности алгоритма и оценки его свойств он был реализован программно с визуализацией исходного множества точек и формируемой невыпуклой оболочки.

На рис. 3 приведены результаты построения вогнутой оболочки, начиная с минимальной выпуклой оболочки (рис. 3 а) при трех различных значений коэффициента детализации γ (рис. 3 б-г).

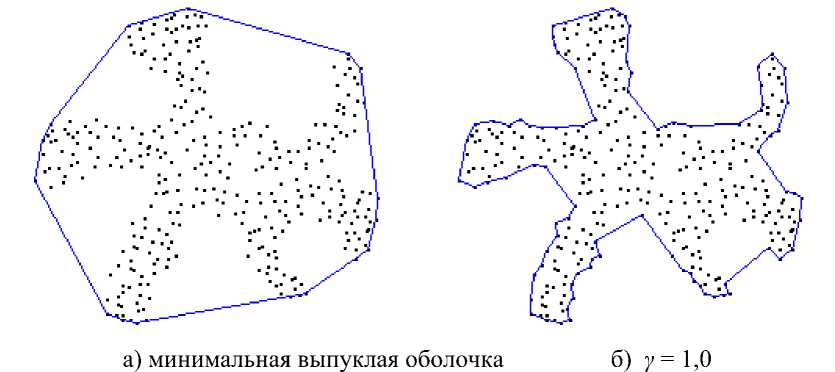
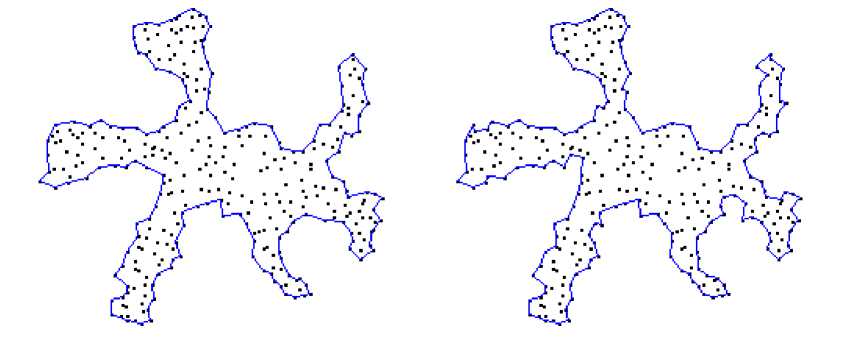
в) γ = 1,5                г) γ = 2,0

Рис. 3 Повышение детализации вогнутой оболочки множества из 340 точек в зависимости от γ

Результаты показывают, что увеличение значения γ повышает возможность формирования все более глубоких впадин вогнутой оболочки, что приводит к возрастанию

Приведенные результаты апробации ал горитма демонстрируют широкий диапа зон возможностей управления детализаци ей вогнутой оболочки.

ее детализация.