Алгоритм преобразования ориентированного графа в ациклический

Ранее авторами работы был построен последовательный алгоритм факторизации вершин ориентированного графа (его детальное описание см. [1]) по отношению циклической эквивалентности. Построенный алгоритм был применен для решения задач, поставленных специалистами по биоинженерии [2-5]. Главным элементом такого анализа является выделение подсетей, выполняющих определенные функции, а также изучение соединений между ними.

Основной трудностью решения таких задач является большое количество вершин и ребер в орграфе. Поэтому появилась идея по аналогии с методом главных компонент в математической статистике упростить исходный орграф путем удаления из него обратных связей с сохранением всех входных и выходных вершин. При этой замене из каждой вершины подграфа должен существовать путь хотя бы в одну выходную вершину, а в каждую вершину должен существовать путь хотя бы из одной входной вершины.

В настоящей работе дается алгоритмическое решение этой задачи. На первом этапе в орграфе выделяются фактор-вершины (классы циклической эквивалентности (кластеры)) и фактор-ребра между ними. В каждом кластере выделяются его входные и выходные вершины. На втором шаге, используя алгоритм фронта волны, каждый кластер заменяется на ациклический подграф, соединяющий входные и выходные вершины кластера. Таким образом, весь исходный орграф заменяется на ациклический подграф, связывающий входные и выходные вершины кластеров.

Формальная постановка задачи

Рассмотрим ациклический орграф A с конечным множество вершин P ( A ) и множеством ребер Q ( A ). На множестве P ( A ) введем отношение частичного порядка: и 1 f и ₂, u 1 , и ₂ e P ( A ), если существует путь из вершины и 1 в вершину и ₂ . Обозначим U ( A ) ( V ( A )) множество максимальных (минимальных) элементов в P ( A ) по отношению f . Множество V ( A ) состоит из вершин, в которые не входят ребра (множество выходных вершин), а U ( A ) состоит из вершин, из которых не выходят ребра (множество входных вершин). Множества U ( A ), V ( A ) могут пересекаться и могут быть пустыми.

Лемма 1. Из любой выходной вершины ациклического орграфа A существует путь в какую-либо входную вершину. В любую входную вершину ациклического орграфа A существует путь из какой-либо выходной вершины.

Доказательство. Пусть и e V ( A ) и U ₀ = { и }, положим, U 1 — множество вершин, в которые можно попасть путем единичной длины из U ₀. Обозначим U ₂ множество вершин из дополнения P ( A )\{ U о u U 1 }, в которые можно попасть путем единичной длины из множества U 1 . Далее по 14

индукции определим множества U k , к >  3 как множество вершин из дополнения P ( A )\{ U о и U 1 и ... и U k - 1 }, в которые можно попасть путем единичной длины из множества U k . Эта рекуррентная процедура закончится на шаге l , так как множество P ( A ) конечно. Тогда все вершины множества U_{ являются входными, U_{ с U ( A ), и из вершины u е V ( A ) можно провести путь в любую из вершин множества U_z . Первое утверждение леммы доказано. Доказательство второго аналогично.

Рассмотрим теперь произвольный орграф A с конечным множеством вершин P(A) и ребер Q(A). Профакторизуем его по отношению циклической эквивалентности: вершина и1 эквивалентна вершине и2, если существует цикл, содержащий обе вершины. Назовем классы циклической эквивалентности фактор-вершинами и обозначим их gi, 1 < i < 5, gi n gj = 0. Из фактор-вершины gi проведем ориентированное фактор-ребро в фактор-вершину gj , если существуют вершины и' е gi, и * е gj, такие, что (и', и *) е Q (A). Тем самым по орграфу A s определяется фактор-граф [A] с множеством фактор-вершин G = [J gi и i=1

множеством фактор-ребер Q * = Q ( A ) \ U Q ( g i ) (среди них есть кратные) . i = 1

Очевидно, что по построению фактор-граф [ A ] является ациклическим.

Каждая фактор-вершина gi — это подмножество множества P(A), в ней можно выделить подмножества входных U (gi) и выходных вершин V (gi), 1 < i < 5. Под входной вершиной кластера понимается вершина, в которую входит ребро извне кластера, под выходной вершиной понимается вершина, из которой выходит ребро вовне кластера. Сопоставим каждому кластеру gi е G, 1 < i < 5, ациклический орграф gi, удовлетворяющий включению U (gi) U V (gi )с P (gi), причем в орграфе gi из любой выходной вершины существует путь в какую-либо входную вершину, а в любую входную вершину существует путь из какой-либо выходной вершины. Соединим входные и выходные вершины ациклических орграфов gi, 1 < i < 5 ребрами из множества Q * (состоит из ребер, идущих из выходных вершин одних кластеров во входные вершины других класте-s ров) и обозначим A орграф c множеством вершин P(A) = |JV(gi) и U(gi) i=1

и множеством ребер Q ( A ) = Q *. Из построения орграфа A вытекает следующее утверждение.

Лемма 2. Орграф A является ациклическим.

Описание алгоритма

Нашей задачей является замена исходного орграфа A на ациклический орграф A . На первом этапе строится фактор-граф [ A ] , применяя, например, ранее построенный авторами работы экономичный алгоритм [1], и в каждом кластере выделяются входные и выходные вершины .

На втором шаге в каждом кластере g е G выделяется ациклический подграф g . Преобразования кластера g в ациклический орграф g состоит из следующих этапов.

Сначала строим ациклический подграф g орграфа g , содержащий непустое подмножество U ( g ) с U (g) множества входных вершин и множество V (g) всех выходных вершин. Затем строим ациклический подграф g *, состоящий из путей, начинающихся в какой-либо вершине множества U ( g * ) = U ( g ) \ U ( g ) и заканчивающихся в какой-либо вершине множества P ( g ) . Очевидно, что объединение g = g о g * также образует ациклический граф, причем V ( g ) с P ( g ) .

Построение ациклического графа g . Строим ациклический подграф g ', орграфа g , содержащий непустое подмножество U ( g ) с U (g) множества входных вершин и множество V (g) всех выходных вершин. Для этой цели в кластере g реализуем рекуррентный алгоритм фронта волны из множества всех входных вершин U ( g ) до тех пор, пока фронт не пройдет через все выходные вершины V (g):

A o = U ( g ), A_k + 1 = { j £ U A_t : 3 i е A ^ , ( i , j ) е Q ( g ) } , k = 0,..., T - 1,

T = min {k: V (g )с UA}, P (g ') = UAt, V (g )с P (g').     (1)

Из каждой выходной вершины v е V (g), которая обязательно принадлежит одному из построенных множеств, например v е A r ( _v ) , следующей рекуррентной процедурой доходим по графу g' до множества входных вершин:

B v = { v }, B ^ = { i e A r ( v ) — _k - i : 3 j e B^v v ,(i , j ) e Q ( g ') } , k = 0,..., r ( v ) - 1. (2)

В результате в графе g' строится подграф g'(v). Тогда подграф g = U g'(v) ациклического графа g' удовлетворяет следующим соот-veV (g)

ношениям: U B r _{( v} ) = U ( g ) , V (g) c P ( g ) .

Построение ациклического графа g*. Построение графа g * аналогично построению графа g с некоторыми изменениями. Сначала реализуется алгоритм фронта волны из множества P ( g ) , пока фронт не пройдет через все вершины множества U ( g * ) , меняя ориентацию ребер ( i , j ) в соотношении (1) на противоположную ( j , i ) . Далее из каждой вершины u e U ( g * ) реализуется рекуррентная процедура (2) с заменой ориентации ребер ( i , j ) на ( j , i ) .

Пример

Опишем на примере орграфа, представленного графически (рис. 1), работу построенного алгоритма. В рассматриваемом графе выделено 4 класса эквивалентности, на рисунке каждый подграф, являющийся классом эквивалентности, выделен овалом. Для этой цели можно воспользоваться разработанным авторами алгоритмом [1]. Входные вершины обозначены на рисунке квадратами, выходные вершины заключены в серые круги, одна вершина является и входной, и выходной (вершина 2). Остальные вершины обозначены белыми кругами.

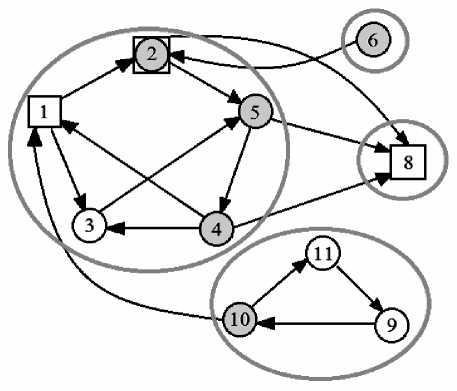
Рис. 1. Исходный орграф

Остановимся на одном кластере данного графа, состоящего из пяти вершин, обозначим его g : U ( g ) = {1,2}, V ( g ) = {2,5,4}. Сначала составим множества A 0 = U ( g ), A = { 3,5 } , A ₂ = {4}, T = 2, так как

• (1,3),    (2,5), (5,4) е Q ( g ), V ( g ) с U A_t .

t = 0

Построим ациклический подграф g ' (рис. 2).

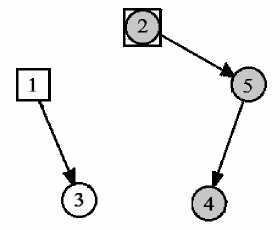
Рис. 2. Ациклический подграф g '

Теперь для каждой выходной вершины v е V ( g ) строим множества Bi :

v = 2: B 0 = {2}, v = 5: B 0 = {5}, B } = {2}, v = 4: B 0 = {4}, B ⁴ = {5}, B ₂ ⁴ = {2}, так как (2,5), (5,4) е Q ( g ') .

Тогда множества вершин и ребер подграфа g состоят из следующих элементов

Q ( g ) = {(2,5), (5,4)}, P ( g ) = {2,5,4}.

Затем аналогичным образом строим ациклический подграф g*, состоящий из путей, начинающихся в вершине 1 множества U (g*) = {1} = = U (g) \ U (g) и оканчивающийся в какой-либо вершине множества P(g). В нашем случае множества вершин и ребер подграфа g* состоят из следующих элементов: Q(g*) = {(1,2)}, P(g*) = {1,2}. Тогда ацикличе ский подграф g = g и g* построен (рис. 3).

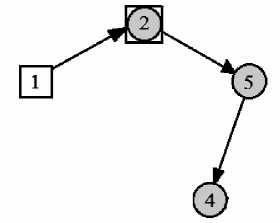
Рис. 3. Ациклический подграф g

Итак, каждому кластеру g е G сопоставляется ациклический орграф g , удовлетворяющий включению U ( g ) U V ( g ) с P ( g ) . Тогда, соединяя входные и выходные вершины ациклических орграфов g ребрами из множества Q ^* , получаем ациклический орграф (рис. 4), содержащий все входные и выходные вершины кластеров.

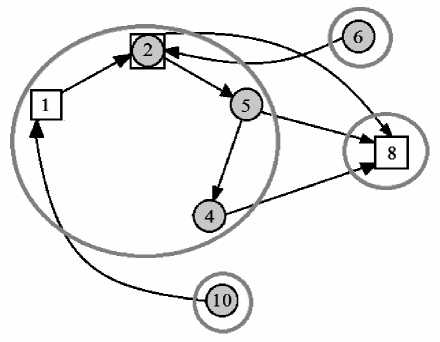
Рис. 4. Ациклический результирующий орграф

Заключение

Совместно со специалистами по биоинженерии построенный алгоритм преобразования ориентированного графа в ациклический был апробирован на белковой сети, получены практические выводы [6].