Алгоритм программы поиска решения двухкритериальной задачи о рюкзаке на основе вычислительного метода

Вычислительный метод решения двухкритериальной задачи о рюкзаке изложен в работе [1]. Разработка алгоритма программы на основе этого метода направлена на поиск практических задач в различных предметных областях. Это является продолжением исследований в данном направлении [2].

Вычислительный метод решения двухкритериальной задачи о рюкзаке

Опишем суть вычислительного метода решения двухкритериальной задачи о рюкзаке. Двухкритериальная задача о рюкзаке (1)

L = Т н=1 k-y i ^ max R = X i=i П-y i ^ min l^in-yi < D y i € {0,1}i = 1,2,...,z

сводится к построению множеств решений (/-1)-ой однокритериальной задачи с целевой функцией L. При построении этих множеств отсекаются неперспективные решения. Это такие решения, которые не могут привести к оптимальному. Неперспективными являются недопустимые решения и решения, удовлетворяющие условию доминирования. В формируемых множествах решения упорядочи- ваются по возрастанию целевой функции L. Кроме того при отсечении по условию доминирования выполняется оптимизация по критерию R.

Далее приведем подробное изложение этого метода. Поиск оптимального решения задачи (1) вычислительным методом сводится к построению допустимых решений z задач вида (2):

L ity ) = Е¹ р=1 ^ р -У р ^ max

R i (y) =Х р=1 Г_р - y_p< D                     ⁽²⁾

i = 23,...,zy p € {0,1}р = 1,2,...,i.

Множество Ci всегда содержит два вектора (0) и (1). Для задачи размерности i строится множество допустимых решений Ci. Элементы Ci упорядочиваются по возрастанию целевой функции. Множество Ci, i=2,3,^,z фор- мируется на основе множества Ci-1. Для каждого вектора yj,1-i = (y1 ,y2,...,y^_1), где j =1,2,...,| Ci-i |, проверяются последующие условия. Если | Ci |=0, то вектор y =

(y{,y{.—’У{_1>)) помещается на первое место в Ci. Если в Ci нет векторов, дающих равное или большее значение целевой функции чем yj,i-i = W ,yJ,...,y2-i), то вектор у = (.У1 ,У2'...,У/-1'0) помещается на последнее место в Ci. Если в Ci есть вектор y21,i, где j1=1,2,…,|Ci|, со значением целевой функции, равным значению целевой функции от вектора yj,i-1, то анализируется условие ЯмС^д-О < Ri(y2i,i). При истинности этого условия вектор у = (у2 ,y2,...,y2_1,0) считается доминирующем над вектором y2i,i и помещается в Ci на его место, а вектор y2i,i отсекается. При ложном значении множество Ci не изменяется. Если в Ci есть вектор y2i,i, дающий большее значение целевой функции чем yj,i-i, то y = (y2 ,yJ,...,yJ-i, 0) заносится перед таким вектором. Если Ki.1(yj,i-1) + ri < D, то вектор y ** = (yi ,yi,...,yi^,1) заносится в Ci на последнее место. Вектора y и y** являются потомками размерности i вектора yj,i-1. Сформированное таким образом множество Сi содержит вектора, упорядоченные по возрастанию значений целевой функции. Выходным данным вычислительного метода является вектор opt, который расположен в Сz на последней позиции.

Алгоритм программы

Приведем блок-схему алгоритма программы (рис. 1-8) на базе описанного вычислительного метода, предварительно представив структуры данных в программе. Эта программа написана на языке Си с использованием системы программирования Visual Studio. На блок-схеме массив строк аt это множество векторов C i-1 ; массив строк аn это множество векторов C i ; строка аt[j] это вектор y _j)i.₁ ; строка ап[]1]П это вектор y _j1,_i ; sD это b i-1 (y j.i -1 ); ^s1 Пэто L f j ); ^s2Dэто Я_и(y^ i ); s3d это K i (y ji,i ).

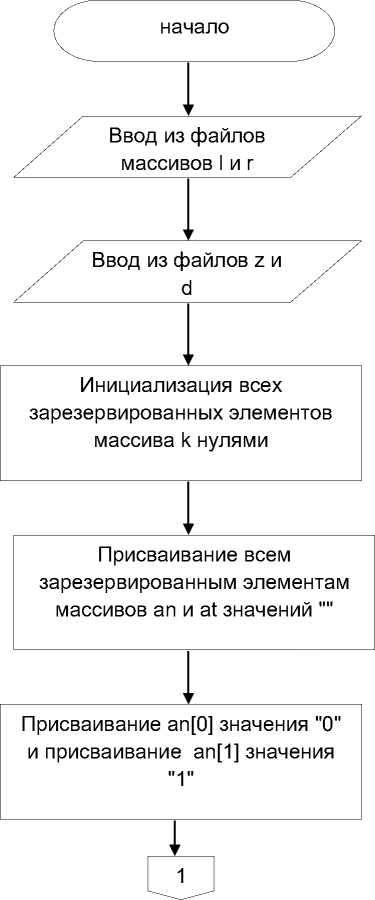
Рис. 1.

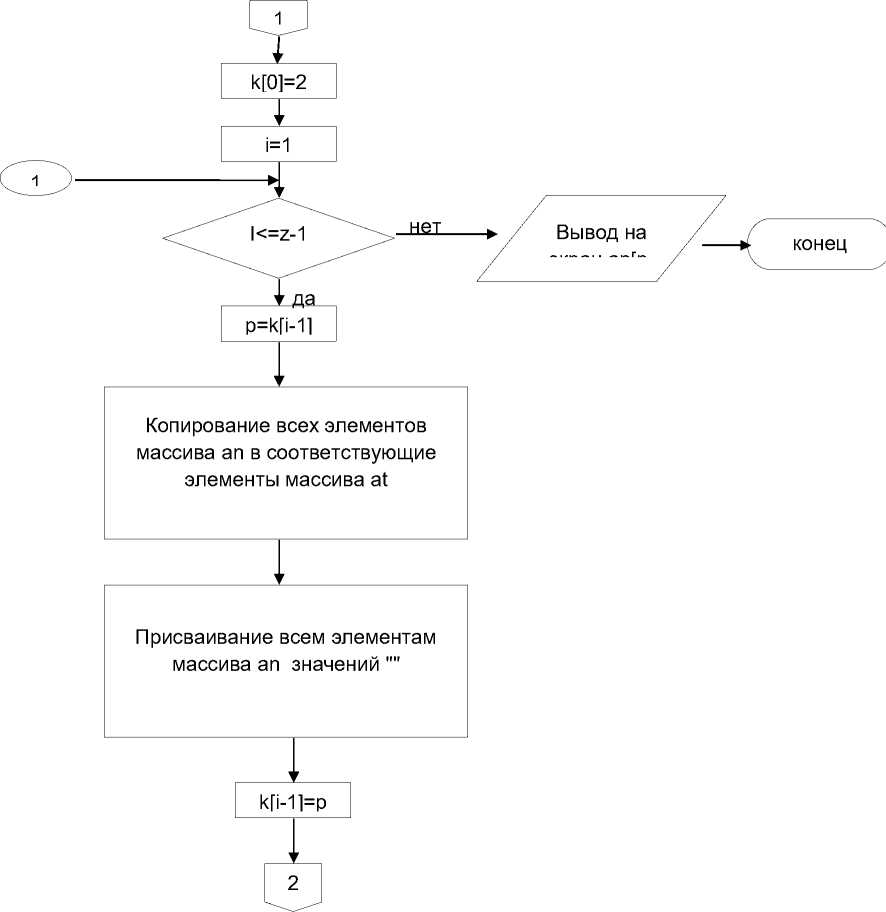
Рис. 2.

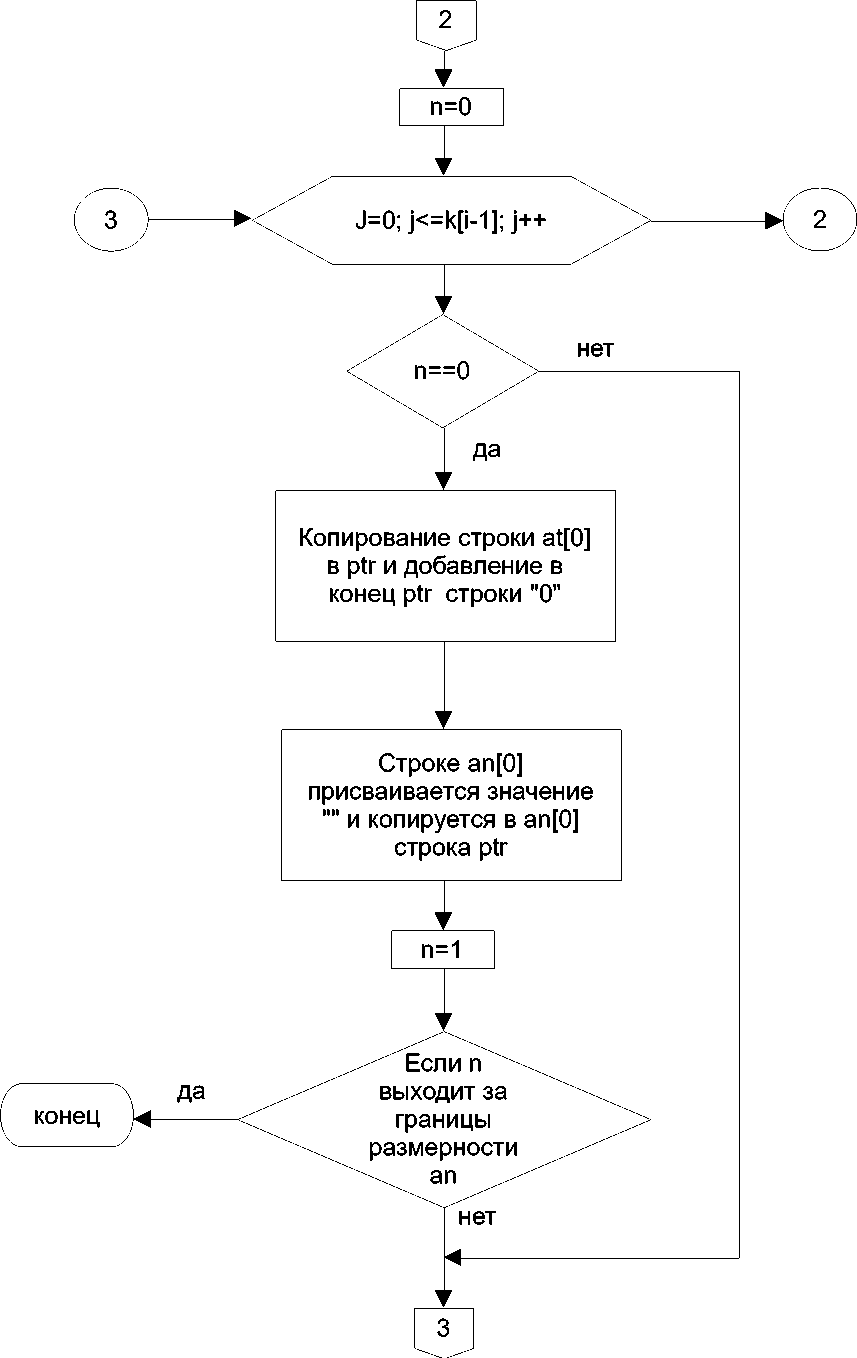
Рис. 3.

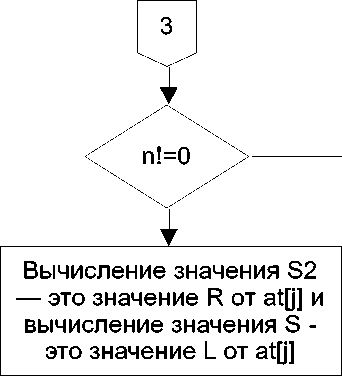
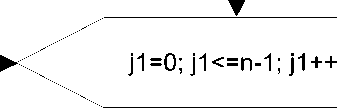
нет

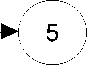
да

Вычисление значения S3 — это значение R от an[j1] и вычисление значения

S1 - это значение L от апЛЦ

Г

Рис. 4.

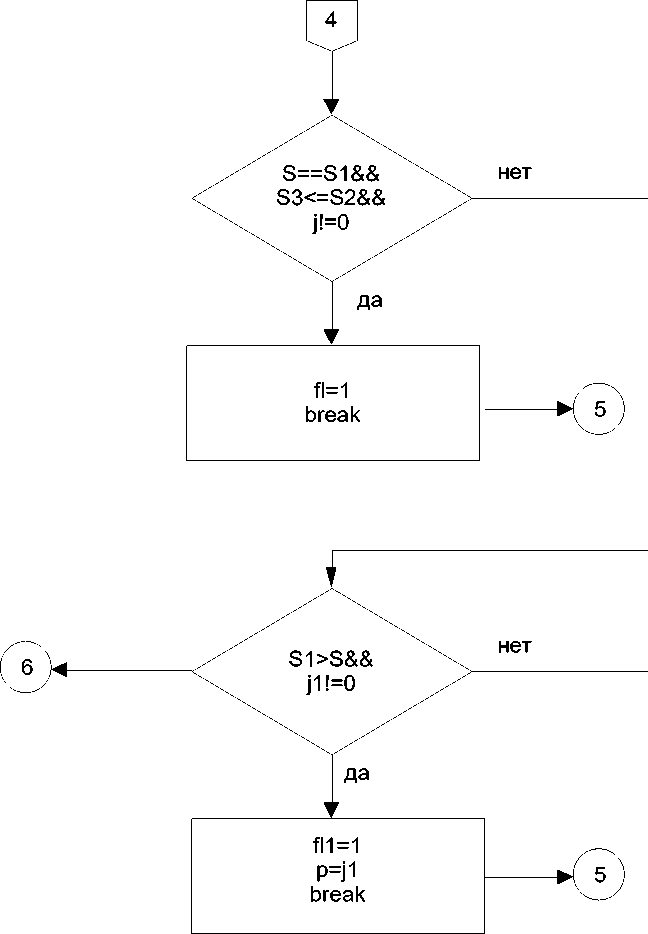
Рис. 5.

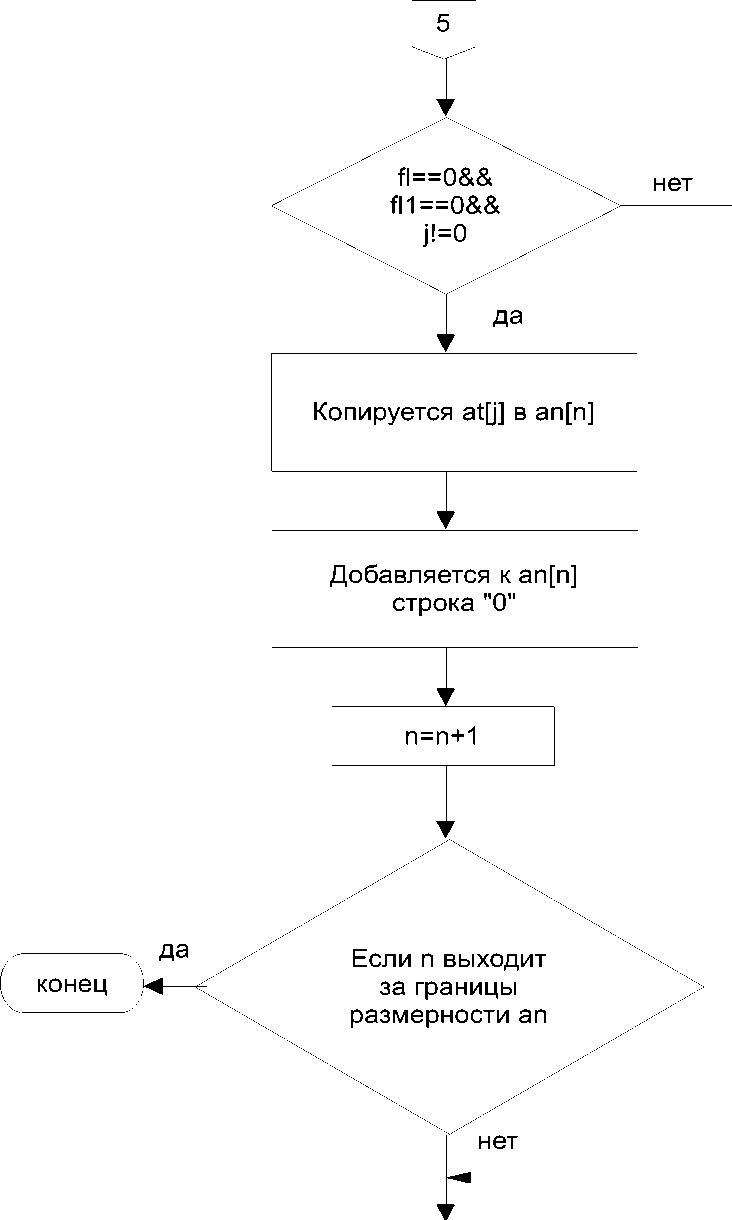
Рис. 6.

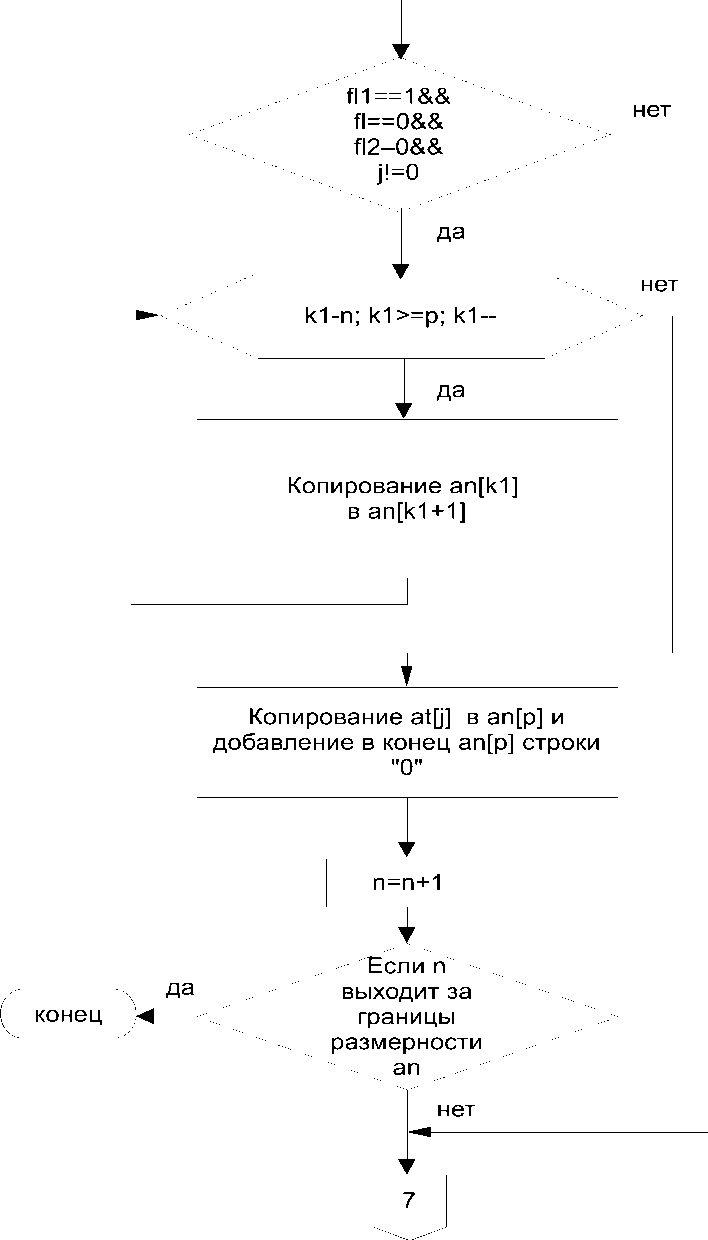
Рис. 7.

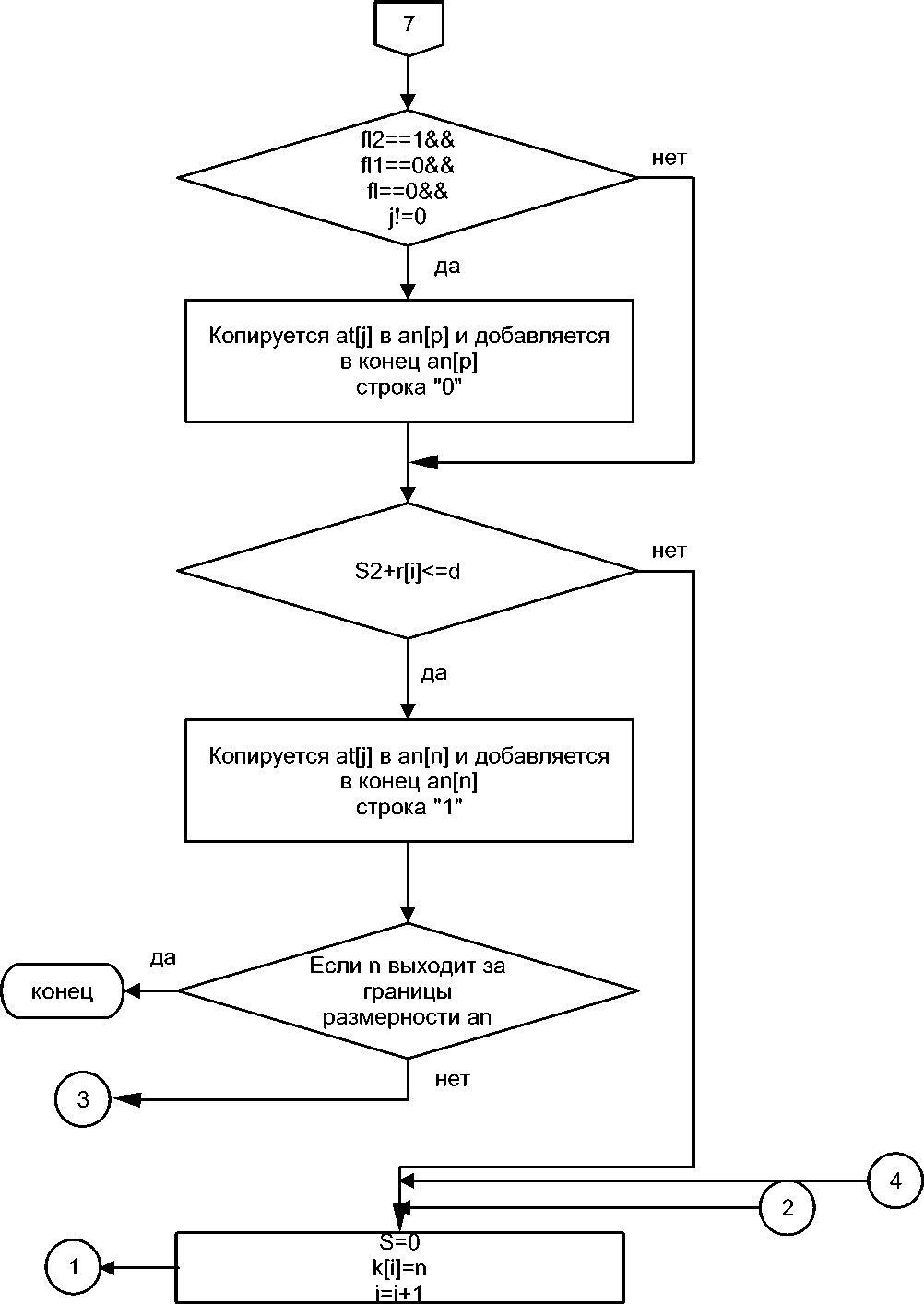
Рис. 8.

Тестирование программы

Программа тестировалась на контрольном примере. В качестве теста использовалась индивидуальная задача (3), полученная из массовой задачи (1).

^(у) = 6-yi + 6-y2 + 12 -Уз^ max

П(у) = 4 - У1 + 4 - У2 + 10 - Уз ^ min

R(y) = 4 - У1 + 4 - У2 + 10 -Уз < D        (3)

z = 3D = 13

У 1 Е {0,1}i = 1,2,3.

Решение задачи (3) определяется тривиально. Это вектор 110. Результаты работы программы на тестирующем примере представлены на рис. 9.

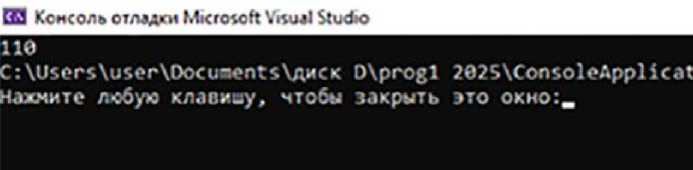
Рис. 9. Результат работы программы

Программа корректно выполнила контрольный пример – ответ 110.

Разработанная программа обуславливает поиск новых практических применений массовой задачи (1).