Алгоритм программы поиска решения многокритериальной булевой задачи по геометрической интерпретации (с количеством критериев m <= 4)

Концептуальное представление метода решения многокритериальной булевой задачи на основе геометрической интерпретации приводится в работе [1]. Разработка алгоритма программы на основе метода направлена на поиск практических приме-

нений рассматриваемой задачи. Что является продолжением исследований в данном направлении.

Рассмотрим постановку многокритериальной булевой задачи в общем виде (1):

С^х) = с 11 • х₁ + с ₁₂ • х₂ + ••• + с _1п ‘ х_п ^ max

С₂(х) = С 21 • X i + С 22 • х₂ + ••• + с_2п • х „ ^ max

Ст(х) = ст1 • X1 + ст2 • X2 + ••• + cmn • хп ^ max(1)

«1(х) = «11 • х 1 + «12 • х2 + ••• + « 1п • хп =b

«2(х) = «21 • х1 + «22 • х2 + ••• + «2п ‘ хп =Ь х£ е {0,1}, i = 1,2,_,п

Далее приведем концептуальное описание метода решения задачи (1) по геометрической интерпретации. Для этого сначала введём переменные:

М₁ = С 11 • х₁ + с ₁₂ • х₂ + ••• + с_1п • х_п

« 2 = с 21 • х 1 + с 22 • х 2 + ••• + с 2п ‘ х п

« т   ^ст1 • ^х1 ^{+ с}т2 ‘ ^х2 ⁺ ••• ^{+ с} mn ‘ ^хп

« т+1 = « 11 ‘ х 1 + « 12 • х 2 + ••• + « 1п ‘ х п

« т+2 = « 21 ‘ х 1 + « 22 • х 2 + ••• + « 2п ‘ х п

На основании системы (2) каждому вектору х_ii = 1,2,„ ^ , 2^п множества решений задачи (1) X = {х₁, х₂, .•. , х₂ п } мощности равной 2^п ставятся в соответствие т троек чисел ⁽ « 1/ « т+1 ,М т+2⁾ , ⁽ U 2 ,U m+1 ,U m+2⁾ ,

•", (ит,ит+1,«т+2). Далее введём множества ____и1={(«', «т+1, «т+2)},у = 1,2п, i = 1, т. Изобразим на рис. 1 элементы множества U1, на рис. 2 -U2 , на рис. 3 - ит. Построение элементов мно- жесте Ul, i = 3, т — 1 подразумевается по умолчанию.

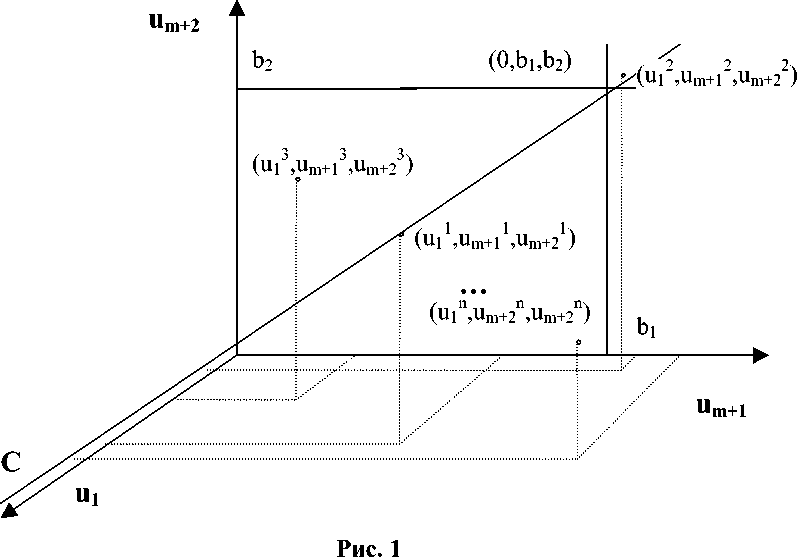
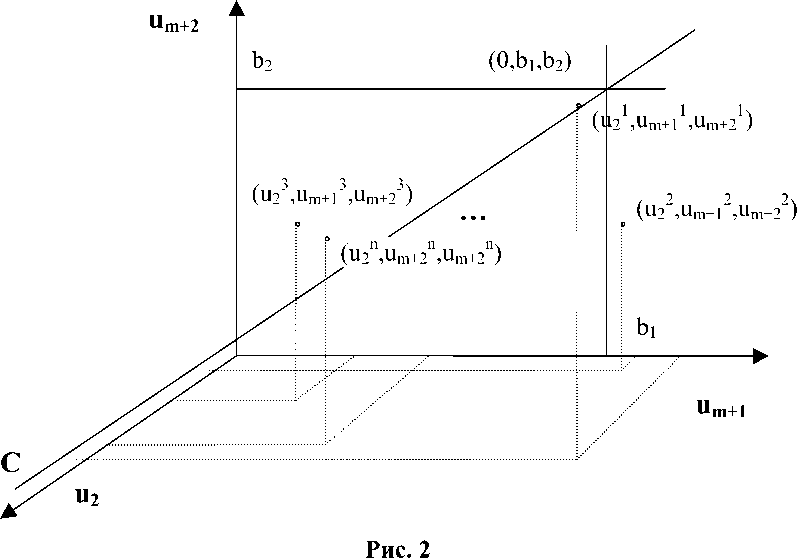
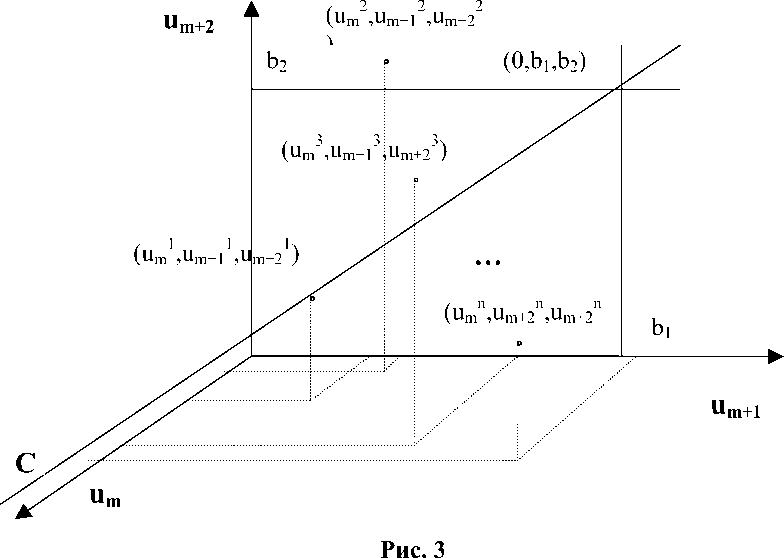
Изобразим на рисунках прямую линию С, на которой все точки соответствуют элементам X, удовлетворяющим ограничениям « 1 (х) и «₂(х) задачи (1). Изобра-

зим также эти ограничения в виде прямых

линий. Определим т точек, расположен-

ных на

на всех

Xj G X дачи

^C вида (u^u^u^i^ ^^т рисунках. Таким образом, элемент

будет (1).

^C 2 ^(xjf)’  •",

оптимальным решением за-

Следовательно,   С₁ (xj^,

^С т ^(x j f )

–

максимальные

значения частных критериев задачи (1).

Далее на основании концептуального описания метода решения задачи (1) представим, в виде блок-схемы, соответствующий разработанный алгоритм программы поиска решения этой задачи. В программе

используются следующие переменные, массивы и файлы:

• -    n – размерность задачи (1);

• -    m – количество критериев задачи (1);

• -    i – параметр цикла;

• -    файл Fileitog.txt – множество X мощности |2ⁿ| решений задачи (1);

• -    вектор x размерности n с элементами int – текущий элемент множества X;

• -    вектор a1 размерности n с элементами double – коэффициенты ограничения a1(x);

• -    вектор a2 размерности n с элементами double – коэффициенты ограничения a2(x);

• -    вектор размерности 4 векторов типа double размерности n – матрица коэффициентов критериев C(j, i), где j=1,2,…,m, i=1,2,…,n;

• -    файл A1.txt – коэффициенты ограничения a1(x);

• -    файл A2.txt – коэффициенты ограничения a2(x);

• -    файл C1.txt – матрица C(j, i), где j=1,2,…,m, i=1,2,…,n коэффициентов критериев;

• -    u_m1 – переменная для хранения

Um+1 = «11 • X1 + «12 • X2 + ... + «1„ • x„;

• -    u_m2 – переменная для хранения

Um+Z = «21 • X1 + «22 ■ X2 + ... + «2n ■ X„;

• -    u – переменная для хранения

Z”=1 Cj,i * Xi,где j = 1 V j = 2 Vj = 3 V j = 4.

Блок-схема алгоритма программы представлена на рис. 4-7. Рисунки 4 и 5 иллюстрируют функционал метода But-ton1_Click. В зависимости от заданного количества критериев m≤4 из него вызываются методы pictureBox1_Paint. picture-Box2_Paint, pictureBox4_Paint, pictureBox5_Paint. Далее на рисунках 6 и 7

представлен функционал метода pictureBox1_Paint. Этот метод строит геометрическую интерпретацию по первому критерию задачи (1) (см. рис. 1). Алгоритм в основе методов pictureBox2_Paint, pic-tureBox4_Paint, pictureBox5_Paint аналогичный алгоритму pictureBox1_Paint, поэтому блок-схемы для них не приводятся.

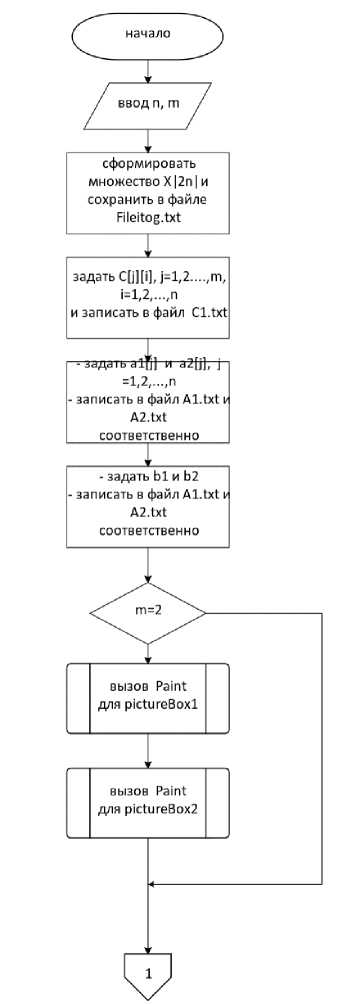
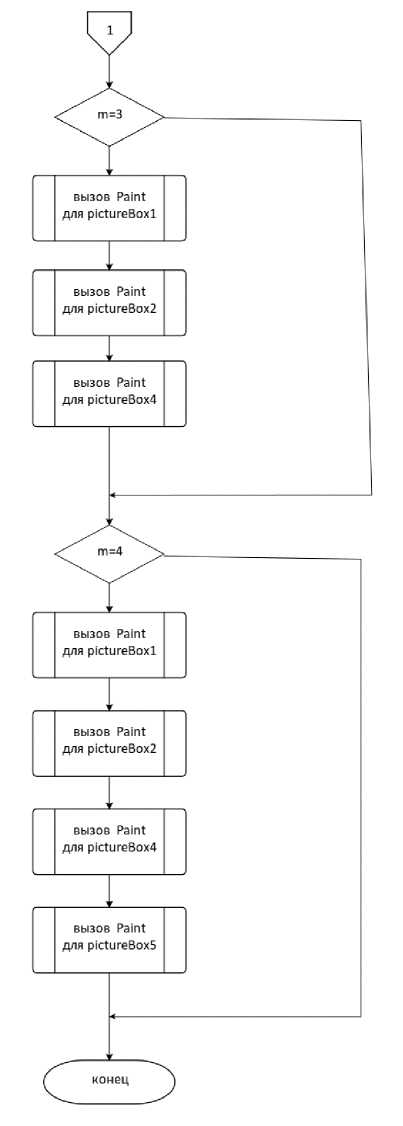
Рис. 5

Рис. 4

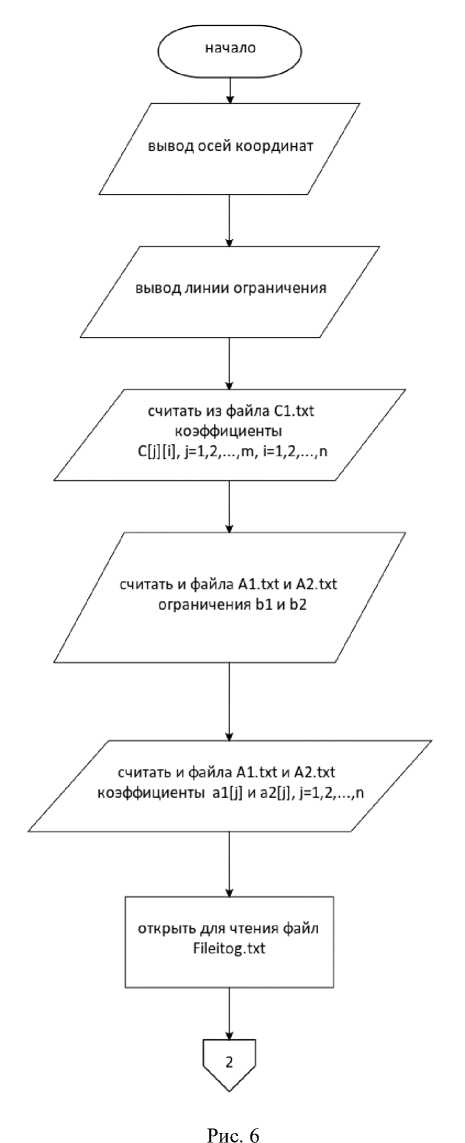
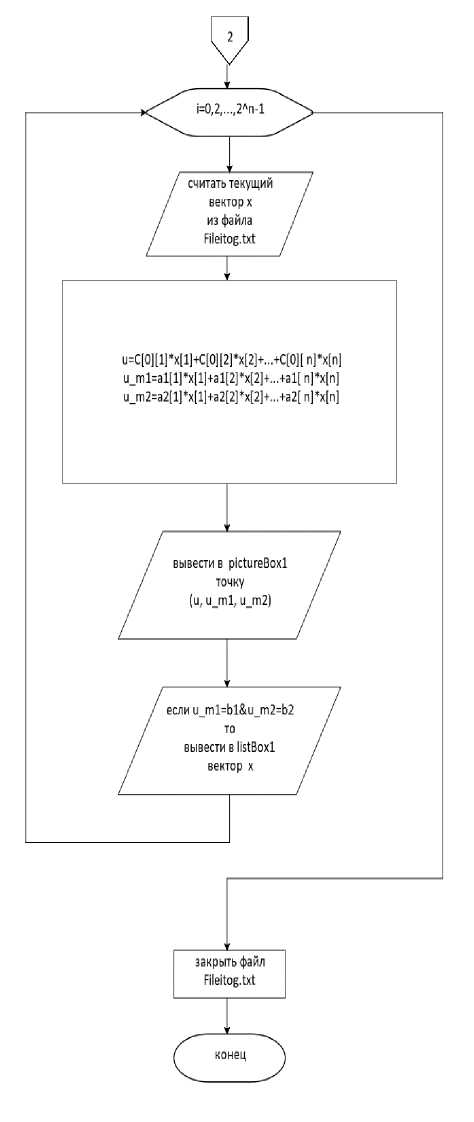
Рис. 7

Программа написана на языке программирования С++ в системе программирования Visual Studio 2022. Для тестирования авторской программы в пакете lp_solve был подготовлен контрольный пример задачи (1) с известным оптимальным реше- нием (рис. 8-9). Для решения задачи (3) в lp_solve была выполнена свертка четырех критериев с весовыми коэффициентами 0,25. Индивидуальная задача (1) для контрольного примера, следующая:

С1(х) = 2 • х1 + 3 • х2 - 5,6 • х3 — 2,8 • х4 ^

С2(х) = 0,8 • х1 + 2 • х2 + 5,2 • х3 — 1 • х4 ^

С3 (х) = 2, 5 • х1 + 2,4 • х2^

С4(х) = 5,2 • х1 + 6 • х2 — 3,4 • х3 ^ max а1(х) = 2 • х1 + 5 • х2 + 3 • х3 — 2 • х4 = 3

а2(х) = 3 • х1 — 4 • х2 + 2,5 • х3 + 1 • х4 = —3

х^{0,1},i = 1,2,3,4

0 LPSolve IDE - 5,5.2.5 - C:\Users\user\DocumentsVHCK: О\статья 2024\контр пример,Ip

□

Idualloop: Objective at iter towdual: Infeasibility sum

-1.40793264521 irl

koidual: Entering column 5, reduced cost -@.4893

File Edit Search Action View Options Help o-eu » gleM * I* a я«if

MAJOR

3 leaves to LOWER,

serformiteration: Variable 5 entered Derformiteration: Feasibility gap at dualloop: Objective at iter rowdual: Infeasibility sum

basis at i I

Й Source Щ Matrix Я) Options A) Result

2xl+5x2+3x3-2x4<—3;

3xl-4x2+2.5x3+lx4<=-3;

telaxed solution

Optimal solution check_solution: Constraint checksolution: Constraint

-le+030

I*

telative numeric accuracy ||*|| =

Jnacceptable accuracy -Found (worse than requires

MEMO: lp_solve version 5.5.2.5 for 32 bit OS, t In the total iteration count 3, 1 (33.3%) There were 0 refactorizations, 0 triggerer ... on average 2.0 major pivots per refai The largest [LUSOL V2.2.1.9] fact(B) had !

Time to load data was ... 1.238 seconds in

was 1, 0.1x NIP ordt inf-norm is 5, with 0.050 seconds, presc simplex solver, in 1

Log Messages

NOD:0

TME: 1,30

Рис. 8

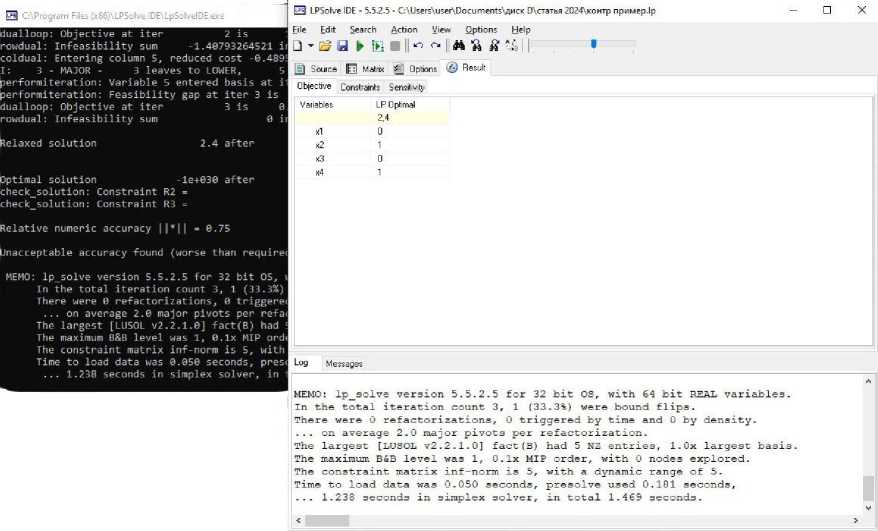
32:1               ITE 2             IPS: 3             INV: 2              NOD:0           TME: 1,30

Рис. 9

Программа определила решение для контрольного примера за 18 секунд. Результат работы программы представлен на рисунках 10 и 11.

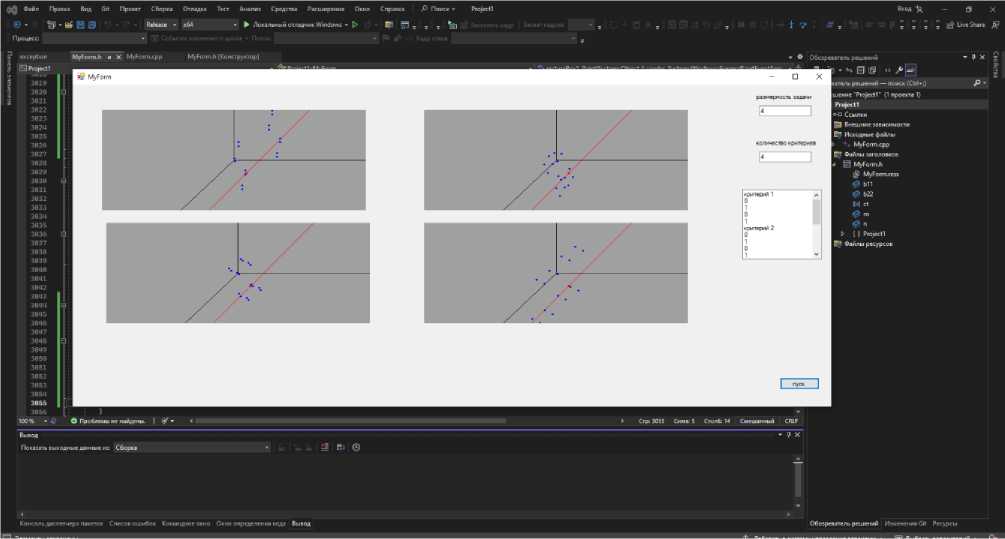
Рис. 10

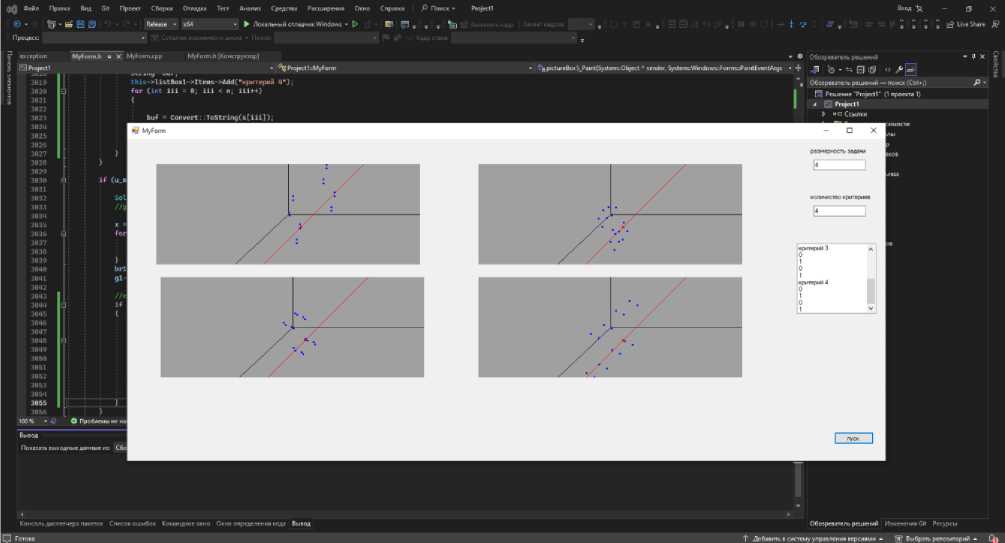
Рис. 11

Разработка программы поиска решения общей задачи (1) дает возможность поиска практического применения этой задачи.