Алгоритм расчета коэффициентов рекурсивного цифрового фильтра второго порядка по заданным требованиям к АЧХ с применением точных расчетных формул

При расчете аналоговых фильтров вследствие нестабильности и разброса параметров входящих в них элементов нет особой необходимости использовать точные, но громоздкие расчетные формулы, поэтому на практике для расчета этих фильтров обычно применяют простые приближенные формулы, а затем характеристики фильтров доводят до требуемых путем подстройки параметров входящих в них элементов. Так как характеристики цифровых фильтров стабильны, поэтому для их расчета целесообразно использовать точные формулы. В устройствах цифровой обработки сигналов широко используются простые в реализации рекурсивные цифровые фильтры (РЦФ) второго порядка [1–5]. Эти фильтры являются цифровыми прототипами аналоговых LC-контуров. В данной статье получены точные расчетные формулы и на их основе разработан алгоритм расчета коэффициентов РЦФ второго порядка по заданным значениям резонансной частоты, полосы пропускания и неравномерности амплитудно-частотной характеристики (АЧХ) в полосе пропускания.

1. Структурная схема, системная функция, комплексный коэффициент передачи и АЧХ РЦФ второго порядка

На рис. 1 приведена структурная схема РЦФ второго порядка и его амплитудно-частотная

характеристика. Все свойства и характеристики этого фильтра зависят от двух его коэффициентов А1 и А2 /1-5/.

Системная функция РЦФ второго порядка на рис. 1 определяется выражением:

H ( z ) = (1 + A 1 z ^{- 1} + A 2 z 2 ) ¹ =

( z - Z 1 )( z - z * )

где z1 = Re- j 0g, z*

z ²

z ² - 2 Re z 1 + | z 1|² ,

= Re j ^{0 g}

– комплексно-сопряженные полюса системной

функции РЦФ в полярных координатах; R –

расстояние от начала координат до полюса в z -плоскости; 0 g = to g / F g — нормированная к частоте дискретизации F _д безразмерная резонансная частота РЦФ. На этой частоте коэффициент передачи РЦФ максимальный. Из выражения для системной функции РЦФ следуют формулы, связывающие параметры R и 0 g с коэффициентами А ₁ и А ₂

0 g = arccos

A 1

2 T A 2 ^J

r = V A 2 ,

A 1 =-2 R cos 0_g,    A ₂ = R ².

Для перехода от системной функции H ( z ) к комплексному коэффициенту передачи K ( j 0) необходимо провести в выражении для H ( z ) замену: z = e j ⁰ , где 0 = to / F g — нормированная к частоте дискретизации F _д безразмерная часто-

K(0V

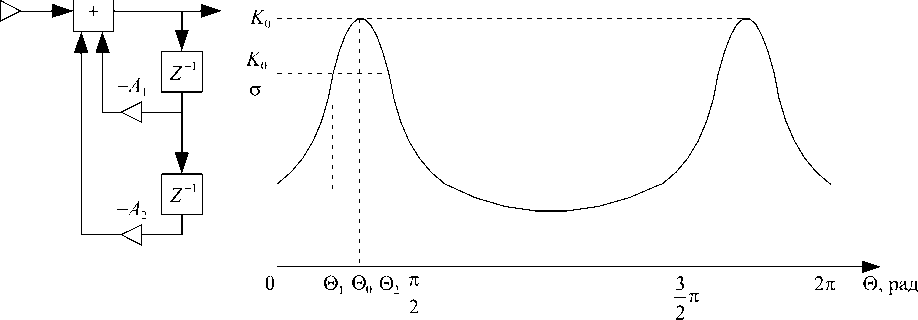
Рис. 1. Структурная схема рекурсивного цифрового фильтра второго порядка и его амплитудно-частотная характеристика

та, причем ω =2π F . В результате такой замены получим:

K ( j θ) =[(1 - Re ^{- j ( θ-θ 0)})(1 - Re ^{- j ( θ+θ 0)})] ^{- 1}.

Это выражение описывает комплексный коэффициент передачи РЦФ второго порядка, схема которого приведена на рис. 1. Для получения выражения, описывающего амплитудно-частотную характеристику (АЧХ) РЦФ второго порядка, необходимо взять модуль от выражения для комплексного коэффициента передачи K ( j θ). Возьмем модуль от K ( j θ) и получим выражение, описывающее АЧХ РЦФ второго порядка:

K (θ) ={[1+ R ² -2 R cos(θ-θ₀)]×

×[1+ R ² -2 R cos(θ+θ₀)]} ^{- 1/2}.

Построенная по этому выражению АЧХ РЦФ второго порядка приведена на рис. 1. Как видно из этого рисунка, АЧХ фильтра периодична по оси абсцисс с периодом 2π.

– коэффициент передачи РЦФ на резонансной частоте θ0. Возведем левую и правую часть уравнения (2) в квадрат и с учетом полученного выше выражения для АЧХ фильтра получим следующее уравнение:

σ²(1- R )²(1+ R ²-2 R cos2θ₀) =

=[1+ R ² -2 R cos(θ₁-θ₀)]×

×[1+ R ² -2 R cos(θ₁+ θ₀)].

Это уравнение является уравнением четвертой степени относительно искомой величины R .

Для его решения введем новую переменную х и после ряда преобразований и замены переменной получим следующее уравнение:

σ² x ( x + A ) =( x + B ₁)( x + C ₁). (3)

В этом уравнении:

(1 - R )² 2 R

A =1 -cos2θ₀

2. Алгоритм расчета коэффициентов РЦФ второго порядка по заданным требованиям к АЧХ фильтра

Задача 1. Необходимо определить коэффициенты А ₁ и А ₂ РФЦ второго порядка по известным резонансной частоте θ₀ и нижней границе полосы пропускания θ₁ при заданной неравномерности σ в полосе пропускания. Для решения этой задачи зададимся неравномерностью σ на нижней границе θ₁ полосы пропускания РЦФ и получим уравнение:

B ₁=1 - cos(θ₁ - θ₀),

C ₁=1 - cos(θ₁ + θ₀).

Решим (3) относительно х . В результате получим:

x =( p ² + Q )^1/2 - p ,

здесь

p=

A σ² - B ₁- C ₁ 2(σ²-1)

Q=

B 1 C 1 σ²-1

K 0

K (θ 1 )

= σ,

где

K ₀=[(1- R )²(1+ R ² -2 R cos2θ₀)] ^{- 1/2}

Определим величину х и из связывающей х и R формулы рассчитаем искомую величину R :

R =1+ x -[(1+ x )² -1]^1/2.                         (5)

Зная R и θ₀, по формулам (1) определим коэффициенты А ₁ и А ₂ РЦФ. Таким образом задача 1 решена. При необходимости для обеспечения на частоте θ₀ единичного коэффициента

передачи фильтра множитель М на входе РЦФ рассчитывается по формуле:

M = ^.                              (6)

K ₀

Задача 2. Определить коэффициенты А ₁ и А ₂ РЦФ второго порядка по известным резонансной частоте 0 q и верхней границе 0 2 полосы пропускания при заданной неравномерности ст. Для расчета величины R в задаче 2 необходимо использовать выражения (3), (4) и (5), в которые вместо коэффициентов B ₁ и C ₁ необходимо подставить коэффициенты В ₂ и С ₂, определяемые по формулам:

B 2 = 1 - c^os(0 2 - ⁰ Q ), C 2 = 1 - ^cos(0 2 + ⁰ 0 ).

Коэффициенты А ₁ и А ₂ определяем по формулам (1), а множитель М по выражению (6).

Задача 3. Определить коэффициенты А ₁ и А ₂ РЦФ второго порядка по известным нижней 0 1 и верхней 0 2 границам пропускания при заданной неравномерности ст на этих частотах. Отметим, что при резонансной частоте фильтра, удовлетворяющей условию:

п 0о * к 2, где к = 1, 2, 3 ... — целые числа, АЧХ РЦФ несимметрична относительно частоты 0О, поэтому для точного решения задачи необходимо разрешить совместно систему из двух уравнений:

I K

K (0 1 ) ' ^K 0 _ K (0 2 )

= ст,

= ст.

После преобразований и замены переменной в этих уравнениях получим систему двух уравнений:

I ст² x ( x + A ) = ( x + B 1 )( x + C 1 ),

^ст² x ( x + A ) = ( x + В 2И x + C 2 ).

Вычтем из первого уравнения второе и после преобразований найдем связь между величинами 0 o , 0 1 , 0 2 и х :

cos 0 + cos 02

cos 0 =----- ¹--------2 .                            (7)

⁰       2(1 + x )

В этом уравнении два неизвестных 0 q и х . Совместное решение этого уравнения с одним из уравнений приведенной выше системы приводит к уравнению четвертой степени относительно x или cos 0 о , которое не удается разрешить в радикалах. Ниже приводится алгоритм приближенного решения задачи 3.

• 1.    Положим 0 о = 0_с р , где 0_с р = (0 1 + 0 2 ) / 2 — среднее значение между 0₁ и 0₂, и по алгоритму решения задачи 1 при известных 0 1 , 0 q и ст определим величину R ₁ по формулам (3), (4) и (5) с коэффициентами B ₁ и C ₁.

• 2.    По алгоритму решения задачи 2 при известных 0 2 , 0 о и ст определим величину R 2 по тем же формулам (3), (4) и (5), но с коэффициентами B ₂ и C ₂.

• 3.    Определим величину R как среднее между R 1 и R 2 по формуле: R = ( R 1 + R 2 ) / 2.

• 4.    Используя вычисленное среднее значение R , определим х по формуле замены переменной:

• 5.    По рассчитанным значениям R и cos 0 q по формулам (1) определим коэффициенты A ₁ и A ₂.

• 3.    Примеры расчета РЦФ второго порядка по разработанным алгоритмам

  Пример решения задачи 1. Задано: Е д = 9600 Гц, F q = 935 Гц, F 1 = 715 Гц, ст = 2. Необходимо рассчитать коэффициенты A ₁ и A ₂ РЦФ, амплитудно-частотная характеристика которого удовлетворяет заданным условиям.

(1 - R )² x =--------.

2 R

Затем по формуле (7) вычислим cos 0 q .

Решение. Вначале необходимо рассчитать нормированные частоты: 0 0 = 2п F q / Е д = 0,612, 0 1 = = 2п F 1 / Е д = 0,468. Затем по формулам (3), (4) и (5) с коэффициентами B ₁ и C ₁ получим R 1 = 0,9305. Тогда по формулам (1) получим: A 1 =-1,523, A 2 = 0,8658. Нормированная АЧХ РФЦ вида Y = K ( 0 ) / K о с этими коэффициентами приведена на рис. 2, а . Из него видно, что на частоте 0 1 неравномерность ст = 1 / Y = 2.

Пример решения задачи 2. Задано: Е д = 9600 Гц, F q = 935 Гц, F 2 = 1155 Гц, ст = 2. Необходимо определить коэффициенты A ₁ и A ₂ РЦФ, амплитудно-частотная характеристика которого удовлетворяет заданным условиям.

Решение. Рассчитаем нормированные частоты 0 q = 2п F q / Е_д = 0,612 и 0 2 = 2п F 2 / Е_д = 0,756. По (3), (4) и (5) с коэффициентами B ₂ и C ₂ получим: R 2 = 0,9097. Тогда по формулам (1) получим: A ₁ = -1, 4899, A ₂ = 0, 8276. Нормированная АЧХ РЦФ с этими коэффициентами приведена на рис. 2, б . Из него видно, что на частоте 0 2 неравномерность ст = 2.

Пример решения задачи 3. Задано: Е д = 9600 Гц, F 1 = 715 Гц, F 2 = 1155 Гц, ст = 2. Необходимо определить коэффициенты A ₁ и A ₂ РЦФ, ам-

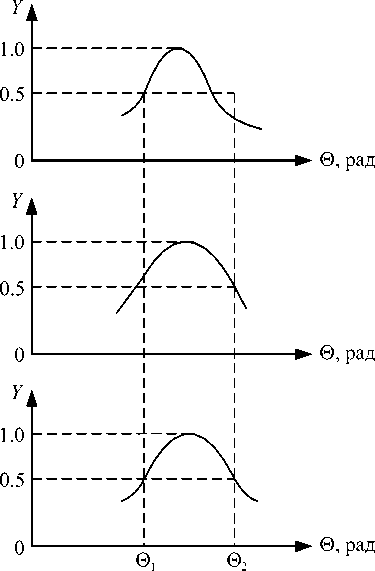
Рис. 2. Нормированные амплитудно-частотные характеристики РЦФ второго порядка, рассчитанные по алгоритмам решения задач 1, 2 и 3

плитудно-частотная характеристика которого удовлетворяет заданным условиям.

Решение. Рассчитаем нормированные частоты 91 = 2пF / f = 0,468 и 02 = 2пF2 / Fg = 0,756. Положим 0Q = 9ср = (91 + 02)/ 2 = 0,612 и при известных 91, 0Q и ст по алгоритму решения задачи 1 получим R1 = 0,9305. Затем по алгоритму решения задачи 2 при известных 00, 02 и ст получим R2 = 0, 9097, далее определим среднее значение R = (R1 + R2) / 2 = 0, 9201. Вспомогательная переменная x = (1 - R2) / 2R = 3, 47 ■ 10 3. Зная значения x = 3,47 ■ 10-3, 01 = 0,468 и 02 = 0,756, по формуле (7) рассчитаем cos 00 = 0,807. Заметим, что величина 00 = arccos 0,807 = 0,6317 в этой задаче не совпадает с величиной 0ср = 0,612. В завершение по формулам (1) рассчитаем ко- эффициенты фильтра A1 =-1,485, A2 = 0,8466. Нормированная АЧХ РФЦ с этими коэффициентами приведена на рис. 2, в. Точный анализ этой характеристики показывает, что на частотах 01 и 02 неравномерность ст = 1,95, а разница между K(01) и K(02) составляет всего 0,1 %. Таким образом, разработанная в этой статье точность приближенного решения задачи 3 вполне достаточна для инженерных расчетов.

Заключение

Полученные в статье формулы для расчета коэффициентов РЦФ второго порядка по заданным требованиям к амплитудно-частотным характеристикам и разработанный на их основе алгоритм точного расчета коэффициентов названных фильтров, удовлетворяющий требованиям к АЧХ этих фильтров, позволит разработчикам радиоэлектронной аппаратуры (РЭА) широко применять эти фильтры в различных радиотехнических устройствах и системах для построения целого класса узлов и устройств РЭА.