Алгоритм расчета констант скоростей переноса химических веществ в гидросфере с использованием геоинформационных систем

Прогнозирование воздействия на окружающую среду антропогенных химических веществ является важнейшей составляющей принятия решений, при выборе химических веществ для их дальнейшего применения в производстве и быту или при оценке потенциального риска при использовании новых веществ (оценка экологического риска) [1]. Для комплексной оценки воздействия на окружающую среду, часто используются многофакторные, интегральные показатели [2]. Системный подход к оценке воздействия на окружающую среду химических веществ выражается в том, что в соответствии с принципом «от колыбели до могилы» оценка воздействия проводится на протяжении всего их жизненного цикла. При применении системного подхода в основе которого лежит методология оценки жизненного цикла в соответствии с ГОСТ Р ИСО 14040-2010 [3] основными задачами являются: оценка количества химических веществ, поступающих в различные подсистемы окружающей среды (атмосферу, гидросферу, почву) и описание их дальнейшего поведения в подсистемах окружающей среде. После посту-

пления в окружающую среду химическое вещество может переноситься в неизмененном виде из одной подсистемы в другую или трансформироваться в ходе физических процессов (испарение, абсорбция/десорбция), претерпевать химические трансформации, такие как фотолиз, гидролиз, окисление или восстановление, радиоактивный распад, подвергаться биотрансформации (биодеградация или аккумуляция в одной или нескольких подсистемах) [4]. Разработано несколько моделей, описывающих поведение химических веществ в окружающей среде [5], которые используются для оценок химической нагрузки на уровне стран [6] или даже целых регионов [7]. Например, в виде программных комплексов реализованы модели: CalTox [8,9,10], разработанная МакКоне с коллегами для оценки воздействия химических веществ в США [1], Simple Box [11], применяемая в Европе для оценки риска воздействия химических веществ, BETR [12], IMPACT 2002 [13], USEtox [14] и др.

В большинстве вышеуказанных моделей при оценках, проводимых на уровне стран или отдельных регионов не учитывается пространственная дифференциация времени пребывания химических веществ в подсистемах окружающей среды, которая наиболее значима для гидросферы поскольку присутствует направленное перемещение веществ с водными массами. Однако рядом авторов было показано, что учет пространственной дифференциации позволяет повысить точность расчетов [15], а ее отсутствие зачастую приводит к снижению достоверности полученных оценок [16,17], что обусловлено различием времени жизни оцениваемого химического вещества на порядки в разных частях исследуемой территории, что характерно, например, для случаев когда расчеты проводятся для локальных систем сопоставимых по размерам с территориями стран и/или регионов [18,19]. Модели, учитывающие пространственную дифференциацию поведения химических веществ в окружающей среде используются рядом исследователей при глобальных оценках химической нагрузки для биогенных элементов таких как фосфор [20,21].

В данной статье авторами изложен алгоритм расчета констант скоростей переноса химических веществ в гидросфере, с использованием геоинформационных систем, который позволит учесть пространственную дифференциацию в этой подсистеме при расчетах химической нагрузки и химического следа. Алгоритм основан на использовании глобальных баз данных, содержащих необходимые данные для всего земного шара с шагом ячейки 0,5°×0,5°, в частности такие данные по рекам собраны в базе данных бассейнов рек Simulated Topological Networks (STN-30p) [22]. Топология данной речной сетки получена на основе цифровой модели рельефа и согласуется с независимыми данными маршрутизации реки. Специфичные для сетки потоки и данные о поверхностном стоке получают путем согласования эмпирических данных о потоках с потоками, рассчитанными с использованием модели водного баланса [23]. Необходимо отметить, что предложенный авторами алгоритм учитывает только движение пресноводных масс, и не позволяет отразить в системе переносы химических веществ осуществляемые морскими или океаническими течениями, движениями воздушных масс и т.п.

ЛОГИСТИЧЕСКАЯ МОДЕЛЬ ЖИЗНЕННОГО ЦИКЛА i-го ХИМИЧЕСКОГО ВЕЩЕСТВА

В ГИДРОСФЕРЕ

Для учета пространственной дифференциации обусловленной движением пресноводных масс систему предлагается представить, как совокупность ячеек размером 0,5°×0,5°.

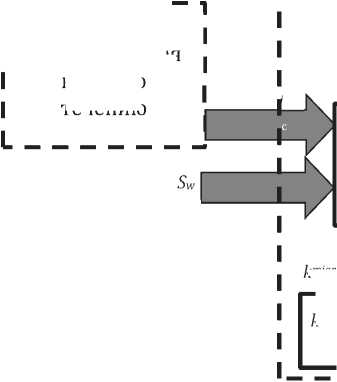
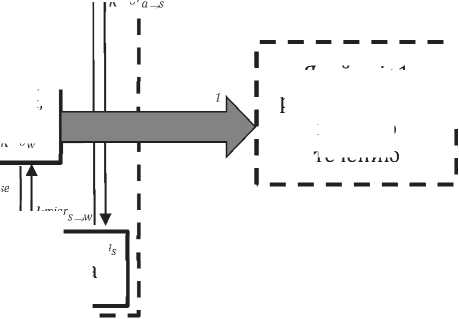
Для учета этих процессов должны быть разработаны дополнительные алгоритмы. Процессы, происходящие в j-ой ячейке исследуемой территории размером 0,5°×0,5° с учетом движения пресноводных масс на некоторой территории (географическом объекте) с определенными границами схематично представлены на Рис. 1.

В представленной на Рис.1 системе в качестве отдельных подсистем выделены атмосфера, гидросфера и почва [24], в которой в качестве отдельно подсистемы (стока) рассматриваются доннын отложения. Жизненный цикл химического вещества в гидросфере в границах оцениваемой ячейки учитывает процессы трансформации или деградации (характеризуется константой скорости k^deg ), миграции (характеризуется константой скорости k^migr ) и переноса (характеризуется константой скорости k^transb ) химического вещества с учетом движения пресноводных масс.

Общее уравнение содержания i-го химического вещества в подсистеме пресноводных объектов j-ой ячейки представлено ниже (формула 1) :

c         migr         migr dmw,l,j _ dmw,i,j , dma^w,l,j . ^ms^w,l>J .

dt dt dt dt dm^migr     drn^migr      drn^migr

, ^dmw^g,iJ , ^dmw^sed,iJ , ^dmw^s,i,j , dt          dt          dt

। Ячейка]

Я ч ейка]+1 рас п оложенная в ыше по

течению

Подсистема пресноводных объектов, включающая в себя реки, озера и водохранилища k desw

k migw ^ sed

k migr_w

Атмосфера№

kmigr kmiSrs^a miSra^w kde0sed Донные отложения

течению kmigr

Почва

Рис. 1. Логистическая модель жизненного цикла химического вещества в гидросфере

Я ч ейка]+1 расположенная н иже по

I

dm

transb w,l,j-l>j

dt

+

dm

transb w,i,j>j+l

dt

, dmWS

⁺ dt "

При наличии стационарного источника поступления i-го химического вещества в j-ю ячейку (dm ^iy /dt = S _Wiij) в пресноводной подсистеме наступает равновесие и, соответственно, ^(dm w,i,j /dt = 0) . В соответствии с концепцией жизненного в алгоритме учтены процессы, которые приводят к изменению количества i-го химического вещества в подсистемах окружающей среды [4,14]:

- миграция химического вещества из одной подсистемы в другую, описывается уравнением (формула 2):

С учетом вышеизложенного формула (1) приобретает вид (формула 5):

^mi g ^{r                 mi} g ^r

0   ^w,i,j + Ka>w,i,j х ma,i,j + Ks>w,i,j х х mS1i1j■—Kw-ga1i1j■ х mW1i1j■—Kw-gsed1i1j■ х mw,i,j — use v         VdgS v          Uransb

АЛГОРИТМ РАСЧЕТА ПАРАМЕТРОВ, ЗАВИСЯЩИХ ТОЛЬКО ОТ СВОЙСТВ ИССЛЕДУЕМОГО i-го ХИМИЧЕСКОГО ВЕЩЕСТВА

miSr , , _ _, migr dmw,i,j /dt     kw,i,j х mw,i,j,     (2)

migr где: kw i j - скорость миграции i-го химического вещества между подсистемами окружающей среды (с-1).

В соответствии с принятой авторами моделью в j-ой ячейке i-е химическое вещество мигрирует в гидросферу из атмосфе-migr         migr ры (dma>w,i,j/dt = ка^№ЛЛ х ^J и почвы (d^^.jM = kSXxj х ms,i,jX В свою очередь из гидросферы вещество мигрирует в атмосферу g^             i.migr

^(dm w^a,i,j ^/dt =. ^K w^a,i,j ^{х m}w,M^{) и в донные} migr               migr „      .

отложения (dmw^sed,i,j/dt = —Kw>sed,i,j х mw,i,j) . Естественная миграция химических веществ в почву незначительна, но i-е химическое ве- щество в значительных количествах может поступать в почву вместе с водой забираемой для сельскохозяйственного и промышленного водопотребления, для того, чтобы отличать это от естественной миграции вместо коэффициента CgV используется коэффициент use migr /jf _L-use

^K w,j ^(dm w^s,i,j ^{/dt     K} w,j ^xmw,i,j⁾ ;

• -    вынос химического вещества за пределы j-ой ячейки, описывается уравнением (формула 3):

dm^/dt = -kw^^sb х m»_№   (3)

где: KWⁱ £ ¹ j ^sb — скорость выноса i-го химического вещества за пределы j-ой ячейки (с^-1). При оценке переноса химического вещества авторы учитывают как вынос химического вещества вместе с пресноводными водотоками в i+1-ю ячейку (dm™ i /dt = -k w^b'₊i х m w,i,j ) , так и внос вещества в i-ю ячейку из i-1-ой ячейки transb         transb

^(dm i,j-l^j / ^{dt k} wi,j-i^j ^{х m} w,i,j-l ⁾ .

• -    деградация химического вещества в ходе протекания химической реакции или радиоактивного распада, описывается уравнением (формула 4):

• ^{d m} w ^eg j ^/dt = ^—C j ^{х m} w,i,j .     ⁽⁴⁾

deg где: Kwij. скорость деградации i-го химического вещества в j-ой ячейке (с-1).

При оценке миграции вещества учитываются два процесса. Первый, это перенос вещества из одной среды в другую за счет диффузии. В этом случае вещество может перераспределяться между средами и перемещаться в обоих направлениях. Оценка этого процесса происходит с использованием коэффициентов распределения. Вторым процессом является перенос за счет адвекции. В результате этого явления вещество также может мигрировать одной среды в другую, например, дождь способствует миграции веществ из воздуха в водоемы.

В расчетах коэффициентов миграции веществ между гидросферой и другими подсистемами окружающей среды для учета процессов, обусловленный диффузией, используются безразмерные коэффициенты распределения веществ: атмосфера/гидросфера и гидрос-фера/почва. Которые в свою очередь оцениваются с использованием безразмерных коэффициентов распределения вещества газ/ жидкость и жидкост/твердое, а также коэффициентов распределения взвешенная фаза / вода и органический углерод/водой. Коэффициент распределения газ-жидкость для i-го химического вещества k_g/li определяется по формуле (6) [25]:

k =   ^25°C,i

g/l,i = 8.31 х 298,

где: Kh25°C j константа Генри для i-го химического вещества моль/(Па*л).

Коэффициент распределения i-го химического вещества жидкость-твердое для недис-социированной k_di и диссоциированной k_ddi форм оцениваемого вещества определяется по приведенным ниже формулам (7,8), полученным после подстановки значений, определенных как константы, в уравнения представленные в [25]:

^fc d,i ^—

^Г О,О5 х fc^ ¹ для недиссоциированных форм веществ О,О4 х 10 ^0,54xlog ( ^fc ow,i ) ^+1,11 для кислот

О,О4 х 1О0,37х1ое(к°№.1)+1,7 для оснований t О,45 х fcJW для амфотерных веществ

^fc dd,i ^— '

О,О5 х fc^ ¹ для недиссоциированных форм веществ

О,О4 х 1О ^0,11х1о е ^(к о№,; ^)+1,54 для кислот

1 для оснований при pK _disII,_i < О

₍   ■ ^^ф ^ко№4 У'¹⁴

О,О4 х 1О^ ^dIS,,, ‘     V¹⁺ fc_O w,J дляоснованийиамфотерныхвприpK _disII,j >О

О,О4 х 1О ^0,11х1о е ^(к о^,1 ^)+1,54 для амфотерных веществ при

^P ^ disI,i ^{+ p} K disII,i < 7

г

1 для амфотерных веществ при

pK disI,i ⁺ P^ disII,i

> 7 и pK _disII,i < О

Hdisni ) ⁰ ’⁶^^^ V’ ¹⁴

V

О,О4 х 1О1     ’     V1+fc0W’J для амфотерных веществ при при pKdisII,i > О где: kow,i коэффициент распределения окта-нол-вода для i-го химического вещества; pKdisIi логарифм константы диссоциации для i-го химического вещества по первой ступени (по умолчанию принимается равным 14); pKdisIIi логарифм константы диссоциации для i-го химического вещества по второй ступени (по умолчанию принимается равным 0).

Дополнительно при проведении ряда расчетов требуется безразмерный коэффициент октанол/вода для i-го химического вещества при нейтральном рН k_owpH7,i, который определяется по следующему соотношению (формула 9).

Доля i-го химического вещества в исходном состоянии, находящегося в воде frw j, принимается равной его долям в почве frsj и в донных отложениях доли frsedj и, при допущении, что pH гидросферы в оцениваемых ячейках по умолча- нию принята равной 7, определяется по соотношению (формула 10).

Массовая доля i-го химического вещества в воде, содержащейся в облаках frcldw,i, при условии, что pH аэрозольной воды содержащейся в облаках по умолчанию принимается 5,6, рассчитывается с помощью соотношения (формула 11).

Коэффициенты распределения i-го химического вещества взвешенная фаза/вода ksusp/w,i (м3/кг) и органический углерод/вода kDOC,i (м3/ кг) при условии, что массовая доля органического углерода присутствующего в виде взвеси в воде в расчетах принимается равной 0,1; массовая доля органического углерода в донных осадка и почве - равной 0,02; плотность минеральной составляющей почвы и донных отложений - равной 2166,3 кг/м3, определяются по формулам (12,13).

^fc ow_pH7,i *

[(■

к

OW’i

1 + 1О ^рК ^1^5/-1 ^—7 + Ю^7-^^ ⁵^

(

к

OW

1 + Ю^^^^-7 + 1О ^7-рЛ-^ ^5//4

и м

Ю^бф^ ош.ф 3,5

1 + 1О ^7-рКя$м + Ю^^^^-7

1О ^°9 ^(к о№,1 ^)- 3, ⁵

)

1 + Ю7-^^4 + Ю^^^-7

)

^п р ^и P ^K disI,i < P ^K disII,i

( 9)

^п р ^и P ^K disII,i > P ^K disI,i

f^ W’i     f^ s,i    f^ sed,i

1 + 1ОР^1$Л1 7 + 1О7 P^disII.i

\ 1 + 1О Р^к^ ^х// , ^{; -7} + 1О ^7- р ^к^^х//,;

■) при pK disI’i < pK disII’i ■ ^ ^{при pK}disII,i >  ^pKdisI,i

f7cZdw,i

{ ⁽ 1 + 1О Р^к^ ^х/ ,г ^-5,6 + 1О ^5,6- р^к^$щ

\ 1 + 1О Р ^к ^=х//,= " ^5,6 + 1О ^5,6_ Р ^к й;х//,;

^ ^{при pK}disI,i <  ^pKdisII,i ^ ^{при pK}disII,i >  ^pKdisI,i

^ susp/wa = ^{2,3 x} (Kt ^x kt + KKi ^{) x} W (12)

kooc.i = 0,08 x kow pH7't .(13)

Доля i-го химического вещества, находящегося в воде в диссоциированной fr_dis,i форме, при условии, что концентрация суспензии в воде для пресных водоемов принимается 0,015 кг/м³ [26], концентрация вещества в биоте - 0,001 кг/ м³, а концентрация органического углерода в воде - 0,05 кг/м³ [25,27], определяются по соотношению (формула 14):

К^л 1₊к_5и5р / _да , ₄хо,5х10 - ⁵ +к_сос ,1 Х5х10 - ⁶ +ВСР ( Х10 - ⁶ ’ ⁽¹⁴⁾ где: BCF_i коэффициент биоконцентрации для i-го химического вещества (м³/кг).

В первой части алгоритма (рис.2) рассчитываются параметры, зависящие исключительно от свойств самих веществ.

Расчет параметров, из части алгоритма блок-схема которого представлена на Рис. 2 не требует использования геоинформационных систем.

АЛГОРИТМ РАСЧЕТА ПАРАМЕТРОВ

ПРОИЗВОДИТСЯ С ИСПОЛЬЗОВАНИЕМ ДАННЫХ, СОДЕРЖАЩИХСЯ В РАЗЛИЧНЫХ ТИПАХ КАРТ

Общий объем воды в j-ой ячейке V_j^total определяется из суммы объемов речной воды V_j^riv

Берется как справочная величина, определяется экспериментально или оценивается на основе структурной формулы вещества, например с использованием модель KOWIN

( начало )

Kow для i-го вещества, константа Генри ,

Берется как справочная величина при отсутствии справочных данных pKdisI = 14, а pKdisII =0

./ логарифм константы диссоциации для i-го вещества по первой ступени pKdisI логарифм константы диссоциации для i-го/ вещества по второй ступени pKdisIL/

Расчет коэффициента распределения газ-жидкость

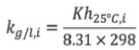
(м3), озерной Vjlake (м3) и воды содержащейся в водохранилищах Vjres (м3). Данные по содержанию озерной воды в j-ой ячейке и данные по объемам воды, содержащейся в водохранилищах для сетки с ячейками 0,5°×0,5° доступны на сайте

Определение содержания в i-ой ячейке речной воды, требует дополнительных расчетов. Ряд ученых, в подобных расчетах предлагает вычислять объем речной воды как произведение неких условных параметров: длины L_j (км), ширины W_j (км) и глубины D_j (км) гипотетической реки присутствующей в j-ой ячейке. В самом простом случае длину условной реки если предположить, что она протекает от одной стороны j-ой ячейки до другой можно вычислить как A _j , однако поскольку большинство рек обладают некоторой извилистостью в расчеты вводится безразмерный поправочный коэффициент извилистости S_bj и длина условной реки определяется по соотношению (ф ормула 15):

L j = S_bJx JA j , (15) где: A_j площадь ячейки вычисляемая для сетки 0,5°×0,5° по ее местоположению (км²).

Коэффициент извилистости для j-ой ячейки Sb,j был рассчитан [28] и определяется в зависимости от порядка реки по соответствующим таблицам составленным для разных материков.

Расчет коэффициентов распределения для диссоциированной и недиссоциированных форм i-гохимического вещества

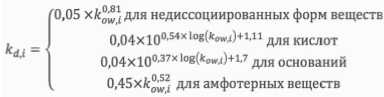
0,05 хк^для недиссоциированных форм веществ 0,04xl0°'llx,oe(*»wi)*1'54 для кислот

1 для оснований при рКцшц < 0

0,04x10 ^w х¹**»»*) для оснований и амфотерных впри рК^шц >0 0,04xl0°'^llx,o^^kow^^+1,54AnH амфотерных веществ при E^^CtP^?^ < 7

1 для амфотерных веществ при ^^^dl^$lL^^!!A > 7 _и рК^щ < 0

kdd.i ~

Определение долей i-го химического вещества в воде, почве и донных отложениях, в соде содержащейся в виде аэрозолей в облаках.

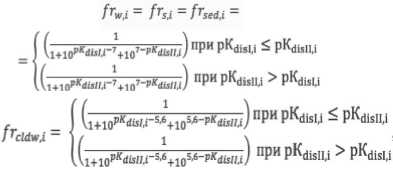
Расчет Kowдля i-го химического вещества при нейтральном pH

.0,04x10 ^aulu ^^wl) для амфотерных веществ при при рК^шц > 0

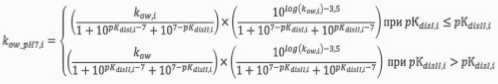
Рис. 2. Блок-схема расчета параметров, зависящих только от свойств исследуемого i-го химического вещества

Определение коэффициентов распределения между взвешенной фаза/вода и органический углерод/вода

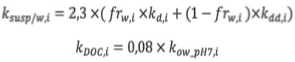
Определение доли i-го химического вещества в воде в дислоцированной форме

<у _ ___i.___________________

* ^'i   1+6_яир/_и,_||х0.5х10"⁵+1соосдХ5х10"⁶+ВСР_|х10"

Сведения о порядке реки для сетки с ячейками 0,5°×0,5° доступны на сайте в качестве одного из параметров базе данных бассейнов рек Simulated Topological Networks (STN-30p) [28]. Ширина и глубина условной реки в j-ой ячейке вычисляется по следующим эмпирическим соотношениям (формулы 16 и 17) [20,29]:

W , = K wix^, ) "" ,      (16)

D ) = ^xlO,;^{1 2}       (17)

где: Кw1, Кw2, Кd1, Кd2, эмпирические константы, которые для глобальных расчетов равны: Кw1 = 5,01*10-2; Кw2=0,52; Кd1=1,04*10-3; Кd2= 0,37 [30].

Wj = 5,01 x IO " ² x (Qj)^0,52.

D j = 1,04 x 10 " ³ x (Q j ) ^0,37 ,

ры в гидросферу в j-ой ячейки v a→w,i,j и из гидросферы в атмосферу v _w→a,i,j по формулам (22,23):

v_a ^ _wi j _ (0,003 + 0,002 x Ws , ) x

V _w ^ _ai, j _ (4 x 10 "⁶ + 4 x 10 "⁷ x Ws , ² ) x

^и^80,035 , (22)

MW i 0,032 ⁰,²⁵ -^wt , ⁽²³⁾

Доля площади исследуемой j-ой ячейки за-

где: Wsj – скорость ветра (м/с) j-ой ячейки 0,5°×0,5° доступна на сайте int/datasets/; MVi – молярная масса i-го химического вещества.

Скорость абсорбции i-го химического вещества в j-ой ячейке v^abs_{a → w,i,j} определяется по формуле (24):

_Vabs _ _fr (________ ^{V a} ^ ^w j, ^{j x} V ^w ^gj,3 ________)

^a ^ ^w,i,j J g ^as,i, j ^a^w,i,j x ka/w,i,j x fYwi + Vw^aga) ^,    '

Cкороcть удаления i-го химического вещества из гидросферы в атмосферу в j-ой ячейке

нятая водой fr^A_w,j вычисляется по уравнению (18):

vvolat w → a,i,j

(м/с) определяется по формуле (25):

fr ^ ■ =

J' w.j

L , xW , + fr^A

lake+res

x A ,

V ^olat — fy , v

^V w^a,i,j ^{_ fr} w,i ^x

^fr dis,i ⁽

^v a^w,i,j ^{x v} w^a,i,j .V a^w,i,j ^x k a/w,i,j ^x tT w,i ⁺ V,

—⁾, (25) w^a,i,j

Aj

, (18)

где: fr^A,lake+res_j – доля площади занятая озерами и водохранилищами, для j-ой ячейки, данные для сетки 0,5°×0,5° доступны на сайте Университета

Нью-Гемпшира

Общая глубина водоемов в j –ой ячейке Dtotali оценивается по формуле:

Dtotal _

y total

frW,jx Aj

Коэффициент распределения i-го химическо-

го вещества между атмосферой и гидросферой

для j-ой ячейки k a/w,i, ka/w,i,j _ kg/l,i

определяется по формуле:

((^U-i™i?| ^8,314^298 Tj^

( (8,314) ^x (298 T j ))    /298\

x e             x (—),

где: Hvapi и Hdisi – энтальпии испарения и растворения (Дж/моль) i-го химического вещества; Tj среднегодовая температура (К) для i-ой ячейки, для сетки 0,5°×0,5° доступна на сайте [25].

Доля i-го химического вещества, находя-

Коэффициенты распределения i-го химического вещества между почвой и гидросферой k_s/w,i и между донными отложениями и гидро-сферой k_sed/w,i , при условии что массовая доля органического углерода присутствующего в виде взвеси в воде в расчетах принимается равной 0,1, а массовая доля органического углерода в донных осадка и почве равной 0,02, определяются по формулам 26 и 27: k s/w,i = ⁰ , ^{46 x (fr} _s , ^x k _di ^{+ (1} - ^fr _s ,. ⁾ X к ду ) (26)

^sed/w,i ^{_ 0} , ^{8 + 0} , ^{43 x k}s/w,i.    ⁽²⁷⁾

Скорость связывания химических веществ в донных отложениях j-ой ячейки v^burial_sedj (м/с) в данных расчетах принимается равной скорости образования осадка на дне водоемов v^acc_sed,j (м/с) в j-ой ячейки [25], которая в свою очередь, при условии, что скорость эрозии сельскохозяйственных и природных почв принимается равной 00,3 мм/год или 9,51*10^-13 м/с, а объемные доли твердых частиц в этих почвах 0,6 [25]; скорость автохтонного производства взвешенных веществ в пресной воде принимается равной 85,74 кг/с [1], концентрация суспензии в воде – равной 0,015 кг/м³, объемная доля твердых частиц в данных отложениях – равной 0,2 [26], рассчитывается по соотношению (формула 28): burial _ ..acc _

^V sed,j ^V sed,j

щегося в газовой фазе в атмосфере j-ой ячейки fr_gas,i,j при условии, что объемная доля воды в воздухе по умолчанию принимается 2,46*10^-13,

2,86 x 10 " ¹² x (fr ^sj + fr as,j ) x A j + 0,2 - 2,3 x 10 " ³ x Q ,

Aj-xyrw"                      ^{, (28)}

определяется по соотношению (формула 21):

frgas,i,j

1 + 2,46 x 10 "¹³

x

(k

^kow p^7,z a/w,i,j ^{x fr}cdlw,i

)

. (21)

Для расчетов переноса за счет адвекции определяются скорости массопереноса через границу раздела фаз i-го химического вещества из атмосфе-

где: frAns,j – доля природных почв в j-ой ячейке (в данном модели берется равной доли сельскохозяйственных почв в соответствующем регионе); frAas,j – доля сельскохозяйственных почв в j-ой ячейке (в данном модели берется равной доли сельскохозяйственных почв в соответствующем регионе); Qj масса перемещающейся из j-ой ячейки воды за год (м3/год) (данные по сред-

ним многолетним значениям Qj для j-ой ячейки сетки 0,5°×0,5° доступны на сайте http://wwdrii. .

Скорость образования донных отложений в

j-ой ячейки vsеd,j (м/с) составляет:

Г2,89 х 10 ^-5 м/с при v f^j < 2 х 10 ^-10 м/с

^Vse^dJ ^— ) асе асе            -10           ^{, (29)}

I     VsedJ при vsed.j — 2 х 10 м/с

Скорость адсорбции i-го химического вещества в донных отложениях v^ads_{w → sed,i} при условии, что скорость массопереноса через границу разделы фаз донные отложения/вода из донных отложений составляет 2,778*10^-8 м/с, а из воды составляет 2,778*10^-6 м/с, определяется по соотношению: v W—sed,; — f dis,i х 2,75 х 10^-8 .    (30)

Скорость накопления i-го химического вещества в донных отложениях v^sed_{w → sed,i} , при условии, что объемная доля твердой фракции в отложениях составляет 0,2, концентрация суспензии в воде – равной 0,015 кг/м³, определяется по соотношению:

Vw-^i — 8,463 х 10^-7 х fr^ i х k s_Ms_p/_w,i , (31)

Cкорость перехода i-го химического веще-

ства из донных осаждений в воду за счет дес-

сорбции v^des_{sed → w i} (м/с) определяется по соотношению (формула (32)):

АЛГОРИТМ РАСЧЕТА КОЭФФИЦИЕНТОВ МИГРАЦИИ И ПЕРЕНОСА ХИМИЧЕСКИХ ВЕЩЕСТВ В ГИДРОСФЕРЕ

Коэффициент миграции i-го химического вещества из атмосферы в гидросферу в i-ой ячейке k ™—W _i j определяется по уравнению (19), при условии, что высота атмосферы в расчетах принимается равной 1 км [25]:

migr _ /, dep ^аД f a ka—w,i,j — \ki + 1000 P^Wj, (34) где: kdepi средняя скорость осаждения i-го химического вещества в атмосферном воздухе (1/с), при проведении подобных расчетах зависит только от свойств самого вещества и берется как стандартная справочная величина или cчитается по стандартной модели USEtox, предложенной UNEP-CETAK [15,25].

Коэффициент миграции i-го химического вещества из почвы в воду в i-ой ячейке k ^-W^j при условии, что глубина почвы принимается 0,1 м, а скорость эрозии сельскохозяйственных и природных почв - равной 00,3 мм/год или 9,51*10^-13 м/с [27], определяется по уравнению:

des ^v sed—w,i

2,56 х 10-8

⁰ , ⁸ + ^k sed/w,i

^k s^mZi,j — ^8,64 х ^{10 5} х

Скорость осаждения твердых частиц i-го хи-

мического вещества в воде за счет ресуспенции в j-ой ячейке равна v^res_{sed → w,j} , при условии, что объемная доля твердой фракции в отложениях

х(-

0,25 х Ral^ + k _s/wi х 9,51 х 10^-13

к i s/w,i

■), (35)

составляет 0,2, определяется по соотношению: res _ „    _ „асе vsed—wj   vsed,j vsed,j.       (33)

На Рис. 3 представлена блок-схема части алгоритма, при выполнении которой расчет параметров произведится в основном с использованием данных, содержащихся в различных типах карт и соответственно для проведения этого блока расчетов, необходимо использовать геоинформационные системы, в качестве которой авторами предполагается использовать геоинформационную систему с открытым кодом QGIS (см. .

На блок-схеме, представленной на Рис. 3, рассчитываемые параметры зависящие только от свойств химического вещества имеют один индекс i, параметры зависящите только от свойств окрущающей среды-параметров ячейки - индекс j, если около параметра присутствуют и индес i и индекс j, то этот параметр использует как данные карт, так и данные о свойствах веществ. Подобное деление может быть оправдано, так как параметры зависящие только от свойств веществ могут рассчитываться без использования ГИС, параметры зависящие исключительно от свойств среды, могут быть рассчитаны только один раз и сохранены в виде соответствующих карт для дальнейших расчетов.

где: Rainj среднегодовое количество осадков (мм/год), для j-ой ячейки, данные для сетки 0,5°×0,5° доступны на сайте Университета Нью-Гемпшира [1].

Константа миграции i-го химического вещества из гидросферы в атмосферу в j –ой ячейке k m- ^g a z j оценивается по уравнению [25]:

voiat ^v w—a,i,j

migr ___________ ^w-a , ^z , ^j fWj х ^ _j ,

Константа миграции j-го химического ве- migr щества из воды в донные отложения k _w-sed,_i,_j. , при условии, что содержание воды и твердых веществ в донных осаждениях по умолчанию принимаются равными 0,8 и 0,2, соответственно [2], а толщина донных отложений принимается равной 3 см, оценивается по уравнению [25]:

kmigr          - w—sed,i,j I

„ ads        sed vw—sed,i ' vw—sed,i ptotal

)-

(

- —

ads        sed vw—sed,i ' vw—sed,i

(

p totaZ

- res ,     , vsed—w,j ^ v

к

res         des vsed—w,j   vsed—w,i

0,03

,^des sed—w,t ' ^v 0;03

, burial sed,j , к dep

^{+ k} sed,i I

)

, (37)

среднее многолетнее количество перемещающейся воды Q,i объем воды в озерах и водохранилищах Vlake,i + Vres,i коэффициент извилистости проточных водоемов Sb,i доля площади ячейки занятая озерами и водохранилищами (%)

	Расчет общего количества воды в i-ой ячейки
	Vtotal,i = Vriv,i + Vlake,i + Vres,i

Расчет длины, ширины и глубины условной реки в j-ой ячейке

Wj = S,01xl0-²x(Q_y)^o52,D_J

l,04xl0-3x(Qy)°'37

Определение доли площади j-ой ячейки, занятой водой л _ LjX Wj+f^^^xAj

—>

Определение средней глубины водоемов в j-ой ячейке vtotal ntotal __ vi JTw,jAi

скорость ветра для ячейки i, Wspid Среднегодовая температура для ячейки j, Т

___________________________________ *

Расчет коэффициента распределения i-го химического вещества между атмосферой и гидросферой в j-ой ячейке

_ //'^нтальпии испарения и растворения, '''"молярная масса, Hvap, Hdis, MW для i-го химического вещества

Расчет коэффициентов распределения 1) между гидросферой и почвой, 2) между почвой и донными отложениями

^a/w,i,j ~ к,;ц Хе

ks/w,l — 0,46 X

^sed/w,i — 0,8 + 0,43x/c_s/_w,_y

Расчет доли i-го химического вещества, находящегося в газовой фазе атмосфере

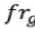
1+2,46х10-13х

Расчет скорости связывания химических веществ в донных отложениях j-ой ячейки и скорости образования осадка на дне водоемов в j-ой ячейки

-.burial _ -.асе _

Определение скоростей массопереноса i-го химического вещества из атмосферы в гидросферу и обратно

2,86xl0"¹²x(fr^_y + fT^xAj + 0,2 - 2,3xlO-³xQj

V,

г>_а^_л1 = ( 0,003 + 0,002 xVKsJx

0,0180035

^fr*j

MW,

(4xl0-6 + 4xl0-7xWsy2)x

О,О320-25

Определение суммарной скорости образования донных отложений

MWt '

^sed.j —

Определение скорости абсорбции i-го химического вещества

2,89x10 ⁵ м/с при v“e4j < 2x10 ¹⁰ м/с ^приг^ггхю-¹⁰ м/с

ydbs

va-»wAJ *vw-*aAj

KV_a^w*j*k_Q/wA4^xfrwA* ^vi

Определение скорости адсорбции j-го химического вещества донными отлож ениями

Расчет скорости удаления i-го химического вещества из гидросферы в атмосферу вj-ой ячейке

Vw^sedA = fr_au (Х2.75Х10-⁸

Vc

ijX^w^aAj

^va^wAjXk_a/w,i,j Xfr„,i+ v,

Расчет скорости накопления i-го химического вещества в донных отложениях

^vw^sed,l — 8,463x10 ^fTiiXk_SUSpj_Wii

Расчет скорости Скорость осаждения твердых частиц i-го химического вещества в воде за счет

«res             _ ..асе vsed-»wJ — vsed,j vsed,j

Расчет скорости перехода i-го химического вещества из донных осаждений в воду за счет дессорбции

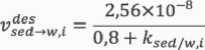
Рис. 3. Блок-схема части алгоритма, при выполнении которой расчет параметров производится, в основном, с использованием данных, содержащихся в различных типах карт йед где: ksedi константа скорости деградации i-го химического вещества при проведении подобных расчетах зависит только от свойств самого вещества и берется как стандартная справочная величина или cчитается по стандартной модели USEtox, предложенной UNEP-CETAK [15,25].

Коэффициент характеризующий поступление веществ из объектов гидросферы в почву за счет водопотребления в j-ой ячейке k “®e при условии, что глубина почвы принимается 0,1 м, определяется по уравнению:

lTi k“s7 = 0,8 X (——-----),    (38)

WJ , V^XA/ где: Iri ирригация в i-ой ячейке (м3/год), для i-ой ячейки, данные для сетки 0,5°×0,5° доступны на сайте Университета Нью-Гемпшира [3].

Учет переноса химического вещества из j-ой ячейки в j+1-ю ячейку оценивается как отношение перемещающейся из j-ой ячейки воды Q_j (м³/год) к общему объему воды, имеющемуся в ячейке V_j^total (м³). Процессы осаждения вещества мы не учитываем в данном коэффициенте, так как они учитываются в коэффициентах описывающих миграцию вещества в донные осаждения. Таким образом, kp y^J^ вычисляется по уравнению (формула 39):

transb _ л /vtotal _ ^i,j^j+1 ^— Vj^/Vj

= Q_jKV}^ake + V/^es + V^rie) , (39)

Константа скорости деградации i-го химического вещества k ^ ^eg при проведении подобных расчетах зависит только от свойств самого вещества и берется как стандартная справочная

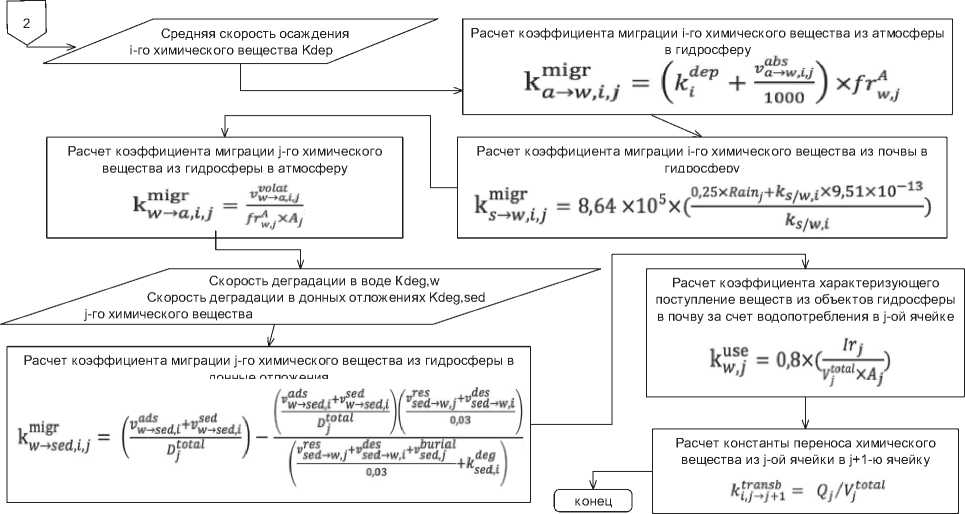
Рис. 4. Блок-схема завершающей части алгоритма расчета констант скоростей переноса химических веществ в гидросфере

величина или считается по стандартной модели USEtox, предложенной UNEP-CETAK [14].

ЗАКЛЮЧЕНИЕ

Авторами был разработан алгоритм в основе которого лежит модификация модели USEtox, предложенной UNEP-CETAK, по расчету концентраций химических веществ в объектах окружающей среды с учетом жизненного цикла. Разработанный алгоритм позволяет при глобальных оценках на уровне мира, отдельной страны или региона учесть пространственную дифферциа-цию времени пребывания вещества в подсистемах окружающей среды, в части учета его переноса с водными массами.