Алгоритм расчета операционных размеров при обработке поверхностей вращения

В работе [1] изложена методика вероятностного расчета размерных цепей, содержащих звенья-эксцентриситеты. В качестве математической модели эксцентриситета принят двух- или трехмерный случайный вектор, алгебраические проекции которого на оси координат есть случайные величины, имеющие нормальное распределение (Гаусса) с нулевым математическим ожиданием и равными дисперсиями сг^ = ст2 _ а2 _ ^2 Величина о в этом случае называется радиальным средним квадратическим отклонением (СКО).

Рассмотрим двухмерный случай (рис. 1). Производится окончательная обработка цилиндрической поверхности заданного радиуса г. Для расчета размера R, выдерживаемого на предшествующей операции (переходе) составляется векторная размерная цепь

Z = R-~r-E&,                                                             (1)

где Z - вектор припуска, нормальный к поверхности, получаемой в результате обработки на рассматриваемом технологическом переходе; г - радиус-вектор этой поверхности; R - радиус- вектор поверхности, получаемой на предыдущем переходе, он подлежит определению; Ед -вектор эксцентриситета поверхности с радиусом г относительно оси поверхности с радиусом R.

Вектор Ед есть разность векторов, имеющих начало в точке О, соответствующей оси ис ходной базовой поверхности:

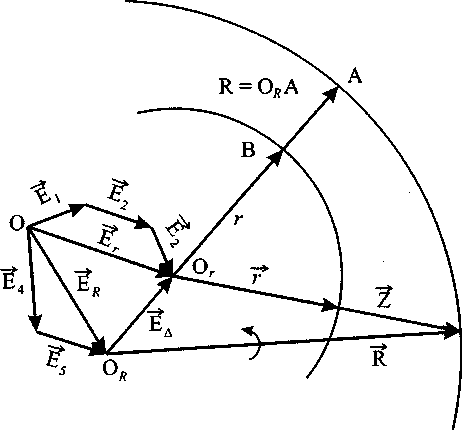
Рис. 1. Векторная размерная цепь

Еь=Ег~Ец.                   (2)

Учитывая, что каждый из векторов Е_г и

—>

Er в общем случае есть векторная сумма нескольких слагаемых (см. рис. 1), выражение (2) запишем в следующем виде:

Ед =Е1 + Е2 + Ез—Ед—Es.          (3)

Суммирование независимых случайных векторов Et в правой части выражения (3) производим, определяя числовые характеристики суммы их алгебраических проекций на оси прямоугольной системы координат. При этом в силу устойчивости закона нормального распределения [2] алгебраические проекции суммарного вектора Ед, рассматриваемые как случайные величины, будут иметь также нор мальное распределение с математическим ожиданием, равным нулю, и дисперсиями, равными сумме дисперсий алгебраических проекций суммируемых векторов Е,:

°д=5>,2.                                                                (4)

i=i где а,- радиальные СКО суммируемых векторов; п - число суммируемых векторов в правой части (3); од - радиальное СКО суммарного вектора.

Поскольку суммируемые векторы Ei имеют круговое нормальное распределение (o_x, = о_у, = о,), то такое же распределение имеет и суммарный вектор Ед, у которого

°хь ~ °уь - °д •

В этом случае модуль вектора Ед распределен по закону Рэлея (или по закону Максвелла для трехмерного вектора).

Поле рассеивания скалярной случайной величины Е, = Ei , подчиняющейся закону Рэлея, принимается равным со,. =2o£(V7 ,                                                                                    (5)

где о£ - СКО случайной величины Е,.

Величина СКО оЕ. связана с радиальным СКО о, (СКО алгебраических проекций случай ного вектора Ei) следующей зависимостью

Учитывая, что со, = E/max -Eimin , при EImin =0 получаем со, = Efmax .

Тогда из соотношений (5) и (6) получаем

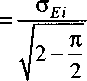
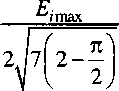
Подставляя соотношение (7) в выражение (4), получаем

°д =

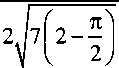
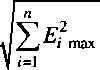
Величина стд является искомым (и единственным) параметром закона Рэлея, которому под чиняется распределение случайной величины Ее.

Для нахождения СКО этой случайной величины вновь используем соотношение (6):

] п                   In

= 0,189

2V7 у i=1                у |=1

Соотношение (9) позволяет вычислять СКО величины эксцентриситета (Е^) поверхности с радиусом г относительно оси поверхности с радиусом R, т. е. СКО модуля вектора Еь, входящего в уравнения (1) и (2). Исходными являются величины Eimax, регламентируемые в конструкторской и технологической документации.

Находим математическое ожидание случайной величины Е^, используя соотношения закона Рэлея:

/ id 2.               / 71       . —. —                                                                                ..

^mEE~s_E\-^=G_EJ-—=19X3(5^.                         (10)

У 2 — Л/ 2 V 4 —71

Возвратимся к рис. 1 и уравнению (1), из которых следует, что величина припуска (модуля вектора Z) различна в разных точках обрабатываемой поверхности с радиусом г. Направление вектора Ее определяет ту точку (В) на обрабатываемой поверхности, где припуск имеет минимальную величину. Это справедливо для любой реализации процесса обработки. Для указанного направления все векторы, входящие в уравнение (1), коллинеарны, поэтому это векторное уравнение вырождается в алгебраическое:

Z = R-r-EE.(И)

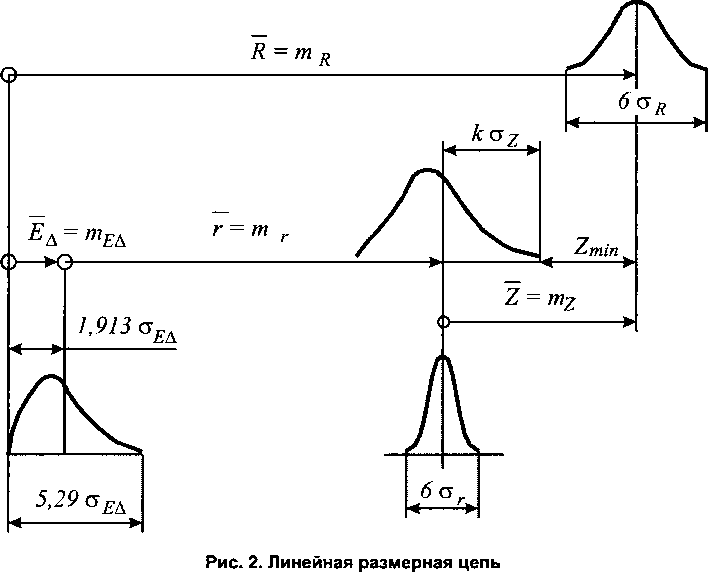
Уравнение (11) - это уравнение линейной размерной цепи (рис. 2). Рассматривая все величины, входящие в это уравнение, как случайные, находим математическое ожидание замыкающего звена - припуска mz = mR “ mr - тЕ\ ■

Среднее квадратическое отклонение величины припуска

^z = j^V^T^”,(13)

где o_R - T_D ; c_r - T_d ; T _D, T _d

- заданные допуски на диаметры соответствующих поверх ностей.

Для определения математического ожидания m_R неизвестного составляющего звена R необходимо знать величину математического ожидания m_z замыкающего звена - припуска Z. Однако регламентируемым значением этого звена является его минимальное значение Z_mm [1].

Случайная величина Z является суммой трех случайных величин, входящих в правую часть уравнения (11). Плотности распределения радиусов R и г описываются законом Гаусса, плотность распределения эксцентриситета Ее - законом Рэлея. Разность радиусов (R-r) распределена также по закону Гаусса [2], тогда закон распределения случайной величины Z есть композиция законов Гаусса и Рэлея. Вид кривой плотности распределения/(z) зависит [3] от величины отношения средних квадратических отклонений

/ =        ............ (14)

V^+^r

При о£Д = 0, т. е. при £д = const имеем композицию двух законов Гаусса, которая снова дает закон Гаусса со средним квадратическим отклонением ctz=V^T+^-                                                     <15>

С вероятностью 99,73 % минимальное значение припуска будет на расстоянии 3oz от его математического ожидания.

Если aR = аг = 0, т. е. R = const, г = const, то распределение плотности замыкающего звена -припуска будет описываться законом Рэлея. Поле рассеивания припуска с вероятностью 99,76 % принимаем равным Ъа^Л = 5,2915о£д (см. выражение (5)). Математическое ожидание припус ка отстоит от минимального значения припуска на расстоянии а = 2о =. V7 - тр

= Ор

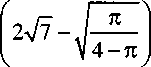
= 3,378сг_£д = 3,378o_z.

Таким образом, в общем случае (см. рис. 2)

^г — ^min "t" коу(16)

где к находится в интервале (3,0; 3,378).

При реальных (для рассматриваемых условий) значениях отношения I = (0.. .4) величина к изменяется от 3,0 до 3,25 [3]. Подставляя (16) в (12), получаем

/Ид = Шг + /И£д + Z^+k ^OR + ^г + ^Ед ■

Для определения величины к может быть использована линейная аппроксимация к = 3+0,06 /,(18)

где I определяется отношением (14).

После вычисления по формулам (17), (18) значения математического ожидания m_R искомого радиуса R находим предельные значения операционного размера

0D^ = 2m_R±^T_D.                                                (19)

Рассмотрим пример. На чертеже детали задан размер 0 40 ± 0,06, что соответствует г = 20 ± 0,03; тг= 20; Td = 0,12; ог = 0,01. В технологической карте заданы отклонения ±0,12 на операционный размер 0D. Тогда TD = 0,24; gr= 0,02. Расчетное значение [1] минимального припуска Zmjn=0,2. Величины допускаемых эксцентриситетов: ЕХтах =0,2; Е2тах =0,15; Е3тах =0,1; ^дшах = 0’2; ^5шах = 0,15 (см. рис. 1). По формуле (9) вычисляем СКО суммарного эксцентриситета о£д = O,189Vo,22 + 0,152 + 0,12 +0,22 + 0,152 = 0,069443.

По формуле (10) подсчитываем математическое ожидание суммарного эксцентриситета.

т =0,069443./^- =0,1328.

£А         V4-TI

По формуле (13) находим СКО припуска oz = Vo,O22 + 0,012 +0,0694432 = 0,07295.

По формуле (14) находим отношение СКО:

_    0,069443

V0,022 +0,012    ’

По формуле (18) находим к = 3 + 0,06x3,1 = 3,186;

toz= 0,2324.

По формуле (17) рассчитываем математическое ожидание mR = 20 + 0,1328 + 0,2 + 0,2324 ~ 20,5652.

По формуле (19) получаем операционный размер

0 41,1304 ±0,12.

Полученный размер округляем в большую сторону до того знака после запятой, который имеют отклонения, и окончательно получаем

D = 0 41,14 ±0,012.

Если поверхность с радиусом г обрабатывается за несколько операций (переходов), то полученный размер D является исходным при расчете операционного размера для предшествующей операции (перехода). Расчет по изложенному выше алгоритму продолжается до получения операционного размера для заготовительной операции (например, штамповки).

Если обрабатываемая поверхность вращения является внутренней (отверстием), то алгоритм расчета операционных размеров остается прежним, но в размерной цепи (11) известным является звено R, а определяемым - звено г.