Алгоритм расчета составных деревянных балок коробчатого поперечного сечения с учетом длительного модуля деформации

На основе теоретического расчета и были получены значения длительного модуля деформации для составной деревянной балки коробчатого поперечного сечения при действии длительной нагрузки для каждой стадии деформирования.

По результатам теоретического расчета длительный модуль деформации для первой стадии деформирования Е^т _дл.1 = 838.078 кН / см ², для второй стадии Е^т _дл.2 = 413.341 кН / см ² (рис. 4.1).

По результатам экспериментальных исследований длительный модуль деформации для первой стадии деформирования Е^э _дл.1 = 467,333 кН / см ², для второй стадии Е^э _дл.2 = 191,950 кН / см ² (рис. 4.2).

Опираясь на полученный данные, был построен график зависимости длительного модуля деформации Е_{дл .} от уровня действующих напряжений σ , который приведен на рис. 4.3.

По графику зависимости длительного модуля деформации от уровня действующих напряжений (рис.4.1) видно, что значения длительного модуля деформации для первой и второй стадии деформирования по данным экспериментальных исследований значительно ниже значений теоретического расчета. Это обусловлено тем, что в конструкции помимо нормальных напряжений возникают дополнительные напряжения, учет которых возможен в дальнейших исследованиях.

График зависимости длительного модуля деформации от уровня действующих напряжений

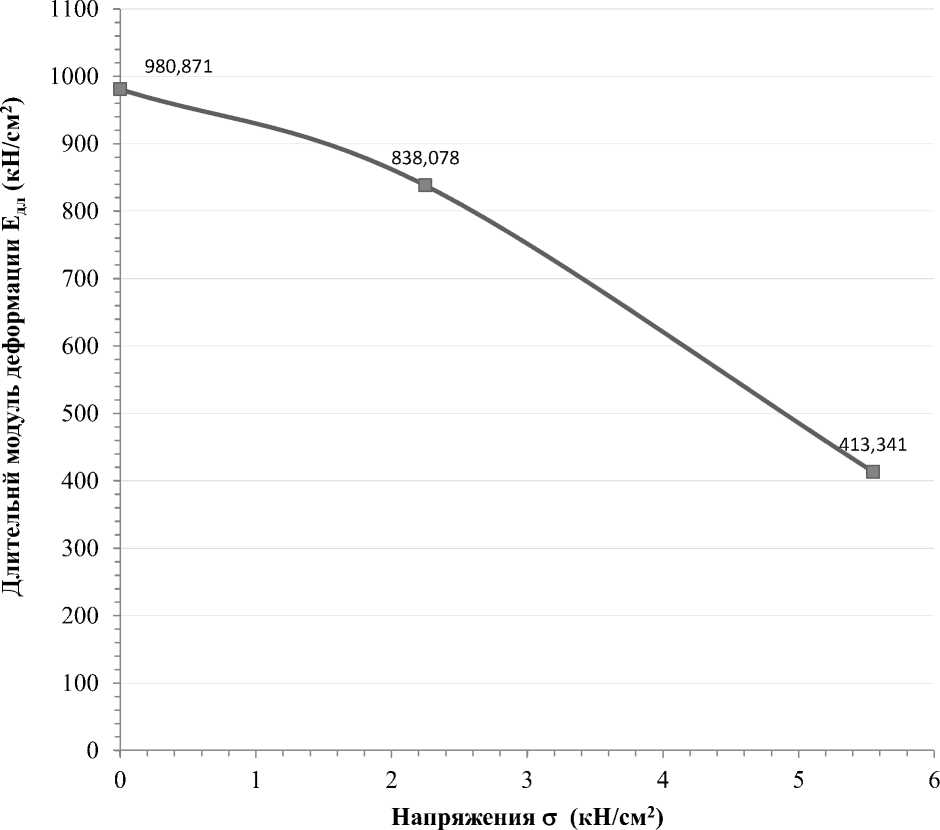
Зависимость длительного мудя деформации от уровня действующих напряжений (теоретический)

Рисунок 4.1 - график зависимости длительного модуля деформации Е дл от уровня действующих напряжений

График зависимости длительного модуля деформации от уровня действующих напряжений

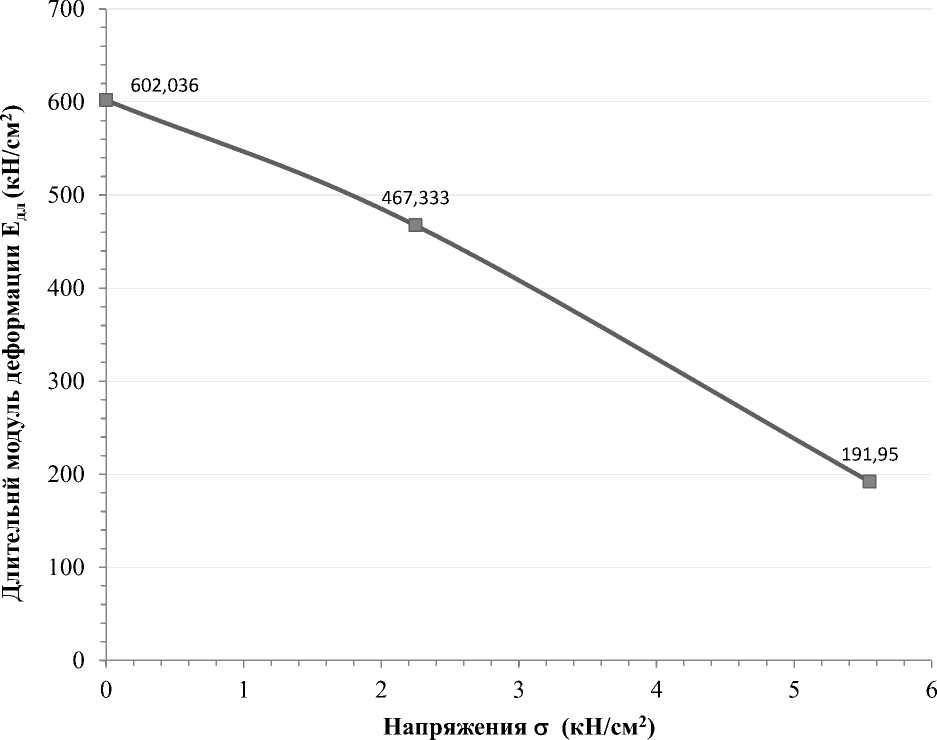
Зависимость длительного модуля деформации от уровня действующих напряжений (экспериментальный)

Рисунок 4.2 - График зависимости длительного модуля деформации Е дл от уровня действующих напряжений

Кривая зависимости длительного модуля деформации от уровня действующих напряжений по данным теоретического расчета имеет схожее очертание с кривой зависимости длительного модуля деформации от уровня действующих напряжений по данным экспериментальный исследований. Исходя из этого, можно сделать вывод о том, что предложенный алгоритм расчета вполне обоснованно может быть применен для расчета конструкций рассматриваемого типа.

График зависимости длительного модуля деформации от уровня действующих напряжений

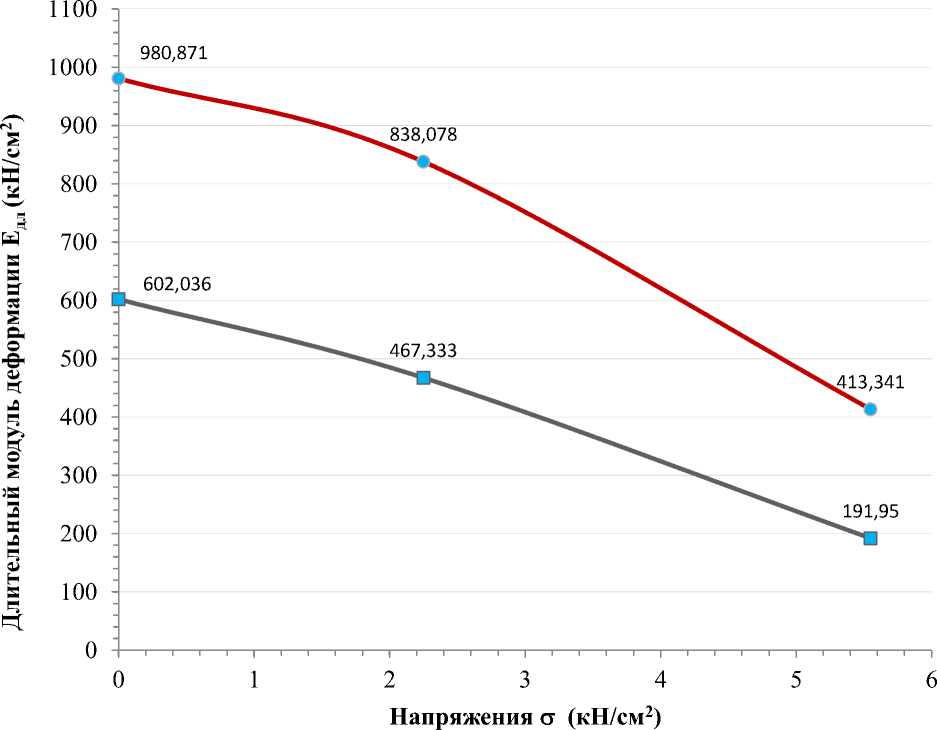
-■-Зависимость длительного модуля деформации от уровня действующих напряжений по данным эксперимента

—•—Зависимость длительного модуля деформации от уровня действующих напряжений по данным теоретического расчета

Рисунок 4.3 – График зависимости длительного модуля деформации от уровня действующих напряжений по данным теоретических и экспериментальных исследований

Алгоритм расчета составных деревянных балок коробчатого поперечного сечения с учетом длительного модуля деформации

Для расчета составных деревянных конструкций коробчатого поперечного сечения используется метод, который позволяет учитывать сложность деформирования древесины во времени при помощи разбиения процессов деформирования на три стадии и замены сложной нелинейной связи между напряжениями и деформациями.

Переход между стадиями происходит при достижении максимальной относительной деформации, критической для каждой из стадий.

Величину критической деформации для первой стадии находим по формуле:

дл

е = Е1 = — = const,                      (4.1)

Н

где о дл - длительный предел прочности (о дл = 2.2 кН/см²);

Н - константа, имеющая физический смысл временного модуля деформации (Н = (0.6 + 0.75)Е ₀ = 962 кН / см 2 );

Е₀ - мгновенный начальный модуль деформации (Е₀ = 1480 кН/ см².).

Величину критической деформации для второй стадии находим по формуле:

^о пп

Е = Е2= --

—

В

^о дл           .

-- = const,

(4.2)

где о пп - кратковременный предел прочности (о пп = 5,5кН/см²);

В

–

константа, имеющая смысл модуля деформации при

критическом нарастании деформаций (В = (0.6 ^ 0.75)Е ₀ = 962 кН / см2.).

Для описания работы деревянных конструкций в области линейной ползучести во всех трех стадиях используем следующую зависимость:

где

E(t) = f(t°)(1 + bt021),

(4.3)

10-2 b = -——--——— --,

0.735 — 0.02086W,

(4.4)

W – влажность древесины.

Если о < одл, то деформации не превышает величины Ег = — л                                                        н

независимо от продолжительности действия нагрузки, и вторая стадия

деформирования не наступает. В том же случае, если о >  о дл , то через

некоторое время t 1 деформации

превосходят величину Е 1 , и начинается

вторая стадия деформирования.

Время перехода во вторую

стадию деформирования t 1 находим по

формуле:

ч-Е^ п

о(Е° — П) ^{(О — О} Дл ^)Е° ,

(4.5)

где н - время релаксации;

о - напряжения (текущие).

При о > — о_дл деформирование начинается сразу со второй стадии. ¹          н  ли

Для выражения кривой ползучести во второй стадии используем формулу:

_Е(й = ^а-^ + 5 °

—

σ дл

пЕ °

к

Z ko" i

Т7" ^(t — ^t[) '

ПЕ 1=0    °

(4.6)

Время перехода в третью стадию деформирования t2 находим по формуле:

£2 - £1

t 2 = t 1 +пЕ о -------.                          (4.7)

^{О — О} Дл

Для выражения кривой ползучести в третьей стадии используем формулу:

О — Оал ®(£-Ы  О — О

e(t) = ——^ е ПЕО--_””.

Вв

Для первой стадии деформирования длительный модуль деформации находим по формуле:

к—1

f(t0)(1 + b(t — t0)0.21)       Де

Едл(to, t) = I l 0Я     ;     07   7 + ) —L (1 + b(t — ti)0-21) I , (4.9)

О(t) О(t)

где o(t) - напряжения, действующие в момент наблюдения t;

e(t₀, t) - относительные деформации, действующие в момент наблюдения t.

Для второй стадии деформирования длительный модуль деформации находим по формуле:

к                     —1

Длительный модуль деформации для третей стадии деформирования находим по формуле:

Е.,М = |^ .-б? —°—^'        ,4.11)

Используя полученные значения длительного модуля деформации, по правилам строительной механики находим прогиб конструкции в каждой стадии деформирования.