Алгоритм решения упругогидродинамической задачи смазки шатунных подшипников

Введение. Различные разделы гидродинамической теории смазки сложнонагруженных подшипников жидкостного трения (СПЖТ) продолжают оставаться в поле зрения специалистов, что связано с большим влиянием этой теории на решение проблемы дальнейшего повышения надежности механизмов и машин.

До недавнего времени расчет гидродинамических подшипников выполнялся при условии, что поверхности трения являются абсолютно жесткими. Стремление конструкторов снизить материалоемкость машин, ведущее к ослаблению жесткости их деталей, возрастающие нагрузки привели к пониманию необходимости учитывать при расчетах гидромеханических характеристик (ГМХ) деформации поверхностей подшипников, максимальные прогибы которых могут быть соизмеримыми с рабочим зазором сопряжения, а размеры области деформирования - с характерными размерами поверхностей трения. Такие подшипники принято называть упругоподатливыми (УП), а режим их смазки - упругогидродинамическим (УГД).

Типичными представителями подшипников с упругоподатливым корпусом являются подшипники коленчатого вала двигателей внутреннего сгорания. Для коренных, особенно шатунных подшипников характерно наличие непрерывного градиента поля деформаций независимо от места приложения нагрузки. Во многих экспериментальных исследованиях подшипников коленчатых валов показано, что существенные расхождения между результатами расчета по теории «жесткого» подшипника и экспериментом во многом обусловлены именно деформациями корпуса подшипника.

Цель решения У ГД задачи смазки состоит в определении ГМХ УП подшипника. К основным ГМХ относят: наименьшее inf h^ и среднее h^ за цикл значения минимальной толщины смазочного слоя, наибольшее sup р_тах и среднее ^^ за цикл значения максимального гидродинамического давления, а также средние за цикл значения расхода смазочного материала Q*, потерь на трение N* и температуры Т* в смазочном слое.

Особенность У ГД задачи смазки состоит в том, что гидродинамические давления, возникающие в смазочном слое, определяются не только реологическими характеристиками смазочного материала, характеристиками микро- и макрогеометрии поверхностей трения и скоростями их относительного движения, но и упругими перемещениями поверхностей трения. Последние вызваны действием гидродинамических давлений на упругий корпус подшипника.

Постановка задачи. В строгой постановке решение У ГД задачи смазки СПЖТ должно опираться на систему взаимосвязанных уравнений, описывающих движение смазочной жидкости в пространстве зазора с учетом ее реологических свойств, реальной геометрии смазочного слоя, схемы подачи смазочного материала, макро- и микрогеометрии поверхностей трения, их упругих деформаций и произвольных движений под действием нагрузок, а также теплонапряженность трибосопряжения.

Определение поля гидродинамических давлений и области его формирования при известном зазоре (положении центра шипа и упругих перемещениях поверхности трения) является предметом гидродинамической части задачи У ГД смазки подшипников скольжения.

До недавнего времени ее решение чаще всего основывалось на решении уравнения Рейнольдса относительно функции безразмерных гидродинамических давлений р^р, z):

5 ( Рр др ) у Г Рр др

^—^py^-WY            w

2 оф от

5р[12Дэ дф j dz (12ДЭ dz , при граничных условиях Свифта-Штибера (СШ), записанных в виде следующих ограничений на функцию р^р^У р^ф, z = ±a)=pa; р(ф, z) = р(ф + 2л:, z); р^ф, z) > 0.                                    (2)

Здесь Ь.р,"Ц_э,р, a - безразмерные толщина смазочного слоя, плотность и вязкость смазки, гидродинамическое давление, ширина подшипника соответственно; фЛ - координаты по углу и ширине подшипника; р_а - безразмерное значение атмосферного давления; со - безразмерное значение относительной угловой скорости шипа. В работе, если не указано иное, используются обозначения статьи [1].

В области источников смазки Qr, где давление постоянно и равно давлению подачи рГ, выполняются условия:

рУр.2^р_г на(ф,2)еП_г,Г = 1,2...Г*,                                          (3)

где Г* - количество источников.

Поле гидродинамических давлений, полученное решением уравнения (1) при граничных условиях (2), (3) не удовлетворяет условию неразрывности течения смазки, поскольку количество жидкости, покидающей активную область смазочного слоя на границе разрыва ф_раз , оказывается не равным количеству жидкости, втекающей в активную область на границе восстановления ФвОС •

Альтернативой условиям СШ являются граничные условия Якобсона-Флоберга-Ольсона (ЯФО):

р^ф,г = ±а)^0", р<Ф^ = Р<Ф^лД\ р{ф_р^ = уРф_раз,^=Ъ^^             (4)

реализация которых обеспечивает выполнение условия неразрывности.

Алгоритмы, с помощью которых решается уравнение (1) при граничных условиях ЯФО, носят название «алгоритмов сохранения массы». Они приобрели популярность благодаря идее Элрода [2] определять поле давлений р^р^ не из уравнения Рейнольдса, а из универсального дифференциального уравнения для некоторой функции б^рДУ описывающей состояние смазки в зазоре подшипника как в несущей области, так и в области кавитации. Функции б^р^ приписывается двоякий смысл. В активной (несущей) области смазочного слоя, где действуют гидродинамические давления, 6 = р/р_с (р_с - плотность смазки при давлении, равном давлению кавитации р_с\ в области кавитации р - р_с,р = р_с. Здесь б^р^ определяет массовое содержание жидкой фазы (масла) в единице объема пространства между шипом и подшипником. В литературе представлено несколько примеров удачной реализации алгоритма сохранения массы к расчету подшипников скольжения с жестким корпусом. Так, в работе [1] предложены модификации уравнения Элрода, позволяющие получать устойчивые численные схемы решения, в том числе и для случая динамического нагружения.

Целесообразность определения гидродинамических давлений на основе модифицированного уравнения Элрода при граничных условиях ЯФО в рамках решения У ГД задачи смазки определяется следующим. Учет упругих свойств корпуса реального шатунного подшипника приводит к нерегулярному изменению геометрии смазочного слоя: его локальным увеличениям или уменьшениям и, как следствие, разрывам слоя смазки, условия реализации которых не могут быть точно описаны граничными условиями типа Свифта-Штибера для уравнения Рейнольдса.

А³ 8

^Мэ 85

(#ф)

^ "I" ^ I¹ + 0 - £^1}+ ;| И ⁺ 0 " g>]}> 2 оф               at

где g- функция переключения:

£(0)=

1, если 6 > 1;

О, если 0 < 1.

Функция Ф^г') связана со степенью заполнения 0^p,z\ определяющей массовое содержание жидкой фазы (масла) в единице объёма зазора между цапфой и вкладышем, соотношением О = 1 + (1 - g) • Ф . В области давлений Ф > 0, g = 1, У = 1 , а Ф-р, где р - безразмерное гидро- динамическое давление. В области кавитации Ф < 0, g = 0,6 -1 + Ф .

Безразмерная толщина смазочного слоя упругоподатливого подшипника, входящая в уравнение (3), определяется выражением h^,t,p^=hngVt,

где /z_rzg(^?,z) = l + Aq^^-^^cos^-^^)) - безразмерная толщина смазочного слоя в «абсолютно жестком» подшипнике; A₀(^,z) - безразмерные макроотклонения формы шипа и подшипника от круглоцилиндрической; j(z),^(z)- безразмерный эксцентриситет центра шипа и угол положения линии центров; W^p.p.t^ - безразмерный оператор упругих перемещений поверхности вкладыша от действующих нагрузок.

Определение «упругих» изменений зазора от известных гидродинамических давлений и других внешних воздействий является предметом «упругой» подзадачи УТД анализа УП подшипников скольжения.

Для шатунных подшипников весь комплекс нагрузок можно разделить на два класса: поверхностные и объемные. До недавнего времени считалось вполне приемлемым решение У ГД задачи, в котором учитывались только распределенные по поверхности вкладыша гидродинамические давления и соответствующие им перемещения РРр(ф,р). В настоящее время доказано [3, 4, 5], что при расчете упругих деформаций корпуса шатунного подшипника влияние его сил инерции на упругое искажение формы поверхности трения Wm ^<р. z) соизмеримо с влиянием гидродинамических давлений. Таким образом, упругие перемещения W^cp/p^ определяются вы ражением

W^p^Wp^pj^Wj^pA(7)

Известные решения УГД задачи смазки шатунных подшипников основываются на конечно элементных моделях упругой подсистемы. В этом случае операторы Wp(ф9p) и Wm^cpA^ в мат ричном виде определяются выражениями:

КМ4/Д(8)

К }=№J,(9)

где ^pY {^„J - векторы безразмерных перемещений узлов на поверхности трения вкладыша подшипника от гидродинамических давлений и инерционных нагрузок; [s] - безразмерная матрица податливости поверхности трения, полученная последовательным приложением единичных нагрузок к каждому узлу поверхности трения; [с] - полная матрица податливости, включающая все узлы конечно-элементной (КЭ) модели; \jp} - вектор действующих безразмерных узловых нагрузок, полученных интегрированием гидродинамических давлений по площади поверхностного элемента; \рт} - вектор безразмерных узловых сил инерции.

Приведенные к узлам конечных элементов силы инерции и, следовательно, перемещения ^_mj, изменяются во времени. При динамическом нагружении многократное использование соотношения (9) существенно увеличивает затраты времени и требуемой оперативной памяти. Учет особенностей динамики кривошипно-шатунного механизма позволил представить перемещения {й^„} суперпозицией четырех упругих решений. Опуская вывод, приведенный в работе [5], в декартовой системе координат проекции на оси х и у вектора безразмерных перемещений узлов на поверхности трения вкладыша нижней головки шатуна записаны как

W^ ” ^^rsin^ + /?)+ wf co^rcos^a + /?)+ w^^ ^{+ w}3 ^з >

W^ ~ ^y(Dx Г COS^X + /?) + W^CpKCOS^a + P^W^O)^ - V^ 8^ .

Здесь w^w* , w{x,wXy - базовые безразмерные перемещения в направлении осей х и у от проекций tetete.} соответственно, \^х }= \^х }= ^т^, где ^т^ - вектор узловых масс; w^w^ - базовые безразмерные перемещения при одновременном приложении сил ^/^^{^^А по оси х и (Дз}= {^л} по оси у; w^w^ - базовые безразмерные перемещения при одновременном приложении сил \fm 3} по оси х и {/„ 2} по оси У >х/ ? Л ~ координаты узлов / -й массы mt КЭ модели (см. рисунок); a - угол поворота коленчатого вала; р - угол качания шатуна; гц = d,

^2 = Р ■

Использование зависимостей (10) позволяет получать перемещения от сил инерции для любого момента времени непосредственно, так как они определяются через базовые перемещения, которые не зависят от времени и режима работы двигателя и могут быть получены для каждой

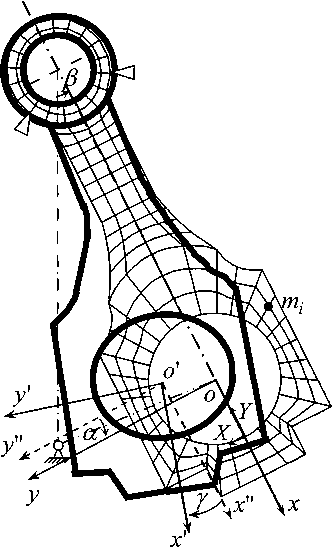
Деформация модели подшипника

конструкции заранее.

Трудности построения КЭ модели заключаются в адекватном описании граничных условий для корпуса шатунного подшипника. Обычно используются кинематические граничные условия, хотя в действительности ни одна из точек реального шатуна не закреплена. Следовательно, ограничение перемещений некоторых узлов КЭ модели может вносить погрешность в вычисления «упругого» изменения зазора. В работах [6, 7] приведена оценка влияния указанного фактора. Показано, что целесообразно использовать модель целого шатуна, закрепляя ее в районе поршневой головки.

Стыковка упругой и гидродинамической подзадач вызывает трудности с точки зрения единства системы координат. Уравнения (1)-(4) записаны в системе координат ХУ, связанной с подшипником (см. рисунок). Из-за деформирования стержня шатуна, а также самой кривошипной головки эта система координат смещается. Упругое поведение кривошипной головки может быть представлено суперпозицией двух состояний: изгиба стержня шатуна при условно «абсолютно жесткой» кривошипной головке и деформированного состояния нижней головки ша туна, определенного относительно ее «абсолютно жесткого» положения. Изгиб шатуна позволяет определить смещение системы координат WQ (ср, р, г), в которой рассматриваются процессы в

смазочном слое. Тогда величины W^

используемые при решении уравнений (1)-(4), представляют собой относительные смещения и определяются из соотношения

(^, Р, ^ = w_p ^ф, р)+W_in (ф, ?) - W_o (ф, р, /).                                                  (11)

В выражении (И) W^tp^t^ - безразмерное относительное смещение системы координат, связанной с подшипником, определяемое как JT₀ (р, р, z) = W_o° (<р, р.^+^оЧф’Р^\^гД^е^о°(р^Р^

- смещения узлов на поверхности трения, вызванные смещением начала координат системы xyz в положение x’^’z” \ W^^рр^ - смещения узлов на поверхности трения, вызванные поворотом системы координат х^'г" на угол у (см. рисунок).

При расчетах величин W^^tp^p^W^ к<р^р^ учитываются как гидродинамические давления, так и инерционные нагрузки. Для вычисления линейного смещения и поворота системы координат используется метод наименьших квадратов и дополнительная матрица базовых углов поворота, определяемая при помощи МКЭ. Более подробно различные варианты расчета смещений системы координат, связанной с подшипником, рассмотрены в работе [5].

Таким образом, решение системы уравнений (5), (6), (И) позволяет при известном положении и скорости центра шипа определить области формирования и величины гидродинамических давлений в УП СПЖТ.

Положение центра шипа шатунного подшипника на смазочном слое j(z), 5^ и его скорости в каждый момент времени цикла нагружения определяются из системы уравнений движения ши па, записанной в виде уравнений равновесия:

^fpxS;

‘ л+/„=°-

Здесь Fx, Fy - проекции внешних сил, действующих на шип подшипника кривошипной го- ловки шатуна; fpx=-^^p^,z^cos^p^ Jp у =-^ ^p^cp,z^sm^^ - проекции сил

Q"

гидродинамических давлений; Q = C1-Q_r - область смазочного слоя, не занятая источниками смазки.

Применение уравнений равновесия вместо формально более точных уравнений движения для высоконагруженных шатунных подшипников вносит в результаты погрешность не более 12%.

При определении теплонапряженности УП трибосопряжений используется предположение об изотермичное™ течения смазки в зазоре. Считается, что все количество теплоты, рассеянное в смазочном слое Л^ , отводится со смазкой, вытекающей в торцы подшипника. Уравнение теплового баланса

4=4 (13) записывается для цикла нагружения. Приращение температуры за цикл нагружения, определяемой на основании уравнения (13), в терминах работы [8] вычисляется по формуле

\T = NlQ_Tpc_m, (14) где N* - среднее за цикл значение мощности, затрачиваемой на трение в смазочном слое; Q_T -среднее за цикл значение расхода смазочной жидкости через торцы подшипника; р и с_т - плотность и массовая теплоемкость смазки соответственно.

Алгоритм решения. Общий алгоритм решения УГД задачи смазки основан на использовании прямой итерационной процедуры с релаксацией перемещений.

Алгоритмом предусмотрен предварительный расчет, который заключается в построении матрицы податливости поверхности трения, матриц базовых перемещений для расчета смещений от инерционных нагрузок. Для этого может быть использован любой стандартный пакет метода конечных элементов, например, «Ansys». Также путем расчета динамики шатунного подшипника двигателя без учета податливости шатуна определяется начальное приближение среднеинте- тральной температуры смазочного слоя и координат положения центра шипа, его вектора скорости и гидродинамических давлений в смазочном слое.

На основном отрезке, в процессе интегрирования уравнений (12), рассчитываются прогнозные значения координат положения шипа, исходя из которых и полученной на предыдущем временном шаге эпюры давлений, по формулам (8)—(11) определяются упругие деформации поверхности трения.

Для исключения влияния на сходимость итерационного процесса резких изменений величины деформаций выполняется их оценка, на основе которой выбирается стратегия расчета поля давлений: если изменение мало, значение релаксационного множителя k_relax принимается равным единице, если же приращение деформаций превышает заданную долю ту толщины смазочного слоя, множитель k_rekax = k¹™^ полагается равным нулю, а затем постепенно увеличивается k^lrdax ⁼ ^reiax ⁺ ^relax ■ Это позволяет поэтапно увеличивать долю деформаций в величине толщины смазочного слоя. Значение Nk_relax подбиралось на основе численных экспериментов. Установлено, что приращение kk_relax зависит от величины абсолютных деформаций и градиента нагрузки, размера шага дискретизации по осям ф и z и др. Для рассмотренных тестовых примеров шаг увеличения kk_relax варьировался в пределах от 0,01 до 0,3 и его применение помогало добиваться устойчивой сходимости итерационного процесса даже при деформациях поверхности трения, сопоставимых с зазором.

Центральным является цикл для определения гидродинамических давлений. Использовалась конечно-разностная аппроксимация модифицированного уравнения Элрода, аналогичная предложенной в работе [1]:

Здесь

2    12// где ЦД2- протяжённости подшипника в направлении координат ф.г ; N,M - количество узлов конечно-разностной сетки в направлении координат ф,2 ; Аг - временной шаг интегрирования в УГД задаче.

Принималось следующее число узлов разностной сетки: N = 96, А^ = 0,0654 рад; М = 25 ; А- =0,0417л.

Учитывая симметрию подшипника по координате z , рассматривается только область -a < z < 0. По оси ф ставилось условие периодичности, на сеточной линии j = Л^/2 + l - условие 5Ф/д2 = 0. На торце подшипников при z = -а: Ф^г = -а) = ^ра -рс\ Безразмерное атмо сферное давление ра соответствует величине 1-105 Н/м2, безразмерное давление кавитации рс соответствует значению 0,9999-105 Н/м2. На границе и в области, занятой источниками смазки, принималось, что Ф^ср^ = ру , где ру - безразмерное значение давления подачи смазки.

Система линейных алгебраических уравнений (13) относительно Фу решается методом Зейделя. Функция g обновляется немедленно после определения Фу. Итерации продолжаются до выполнения условия sK'l-xM/EM510"                             сб)

У            У / У

Здесь 5 - номер итерационного цикла.

Если в ходе решения уравнения Элрода при заданных значениях h после 5 = 20 итерационных циклов критерий сходимости (15) не выполняется, временной шаг А_т уменьшается вдвое.

Необходимо отметить, что неточности в определении поля давлений приводят при расчете упругих деформаций к существенным изменениям толщины смазочного слоя, что, в свою очередь, при повторном решении уравнения Элрода приводит к колебаниям давлений и неустойчивости алгоритма решения У ГД задачи смазки в целом.

При достижении сходимости решения уравнения Элрода и k_rekax = 1 (упругие деформации в толщине смазочного слоя учтены полностью) определяются реакции смазочного слоя. Если прогнозные значения координат положения шипа принимаются - осуществляется шаг по времени, если нет - процедура повторяется. Максимальное значение А/ составляет 1° поворота коленчатого вала (п.к.в.) и изменяется в процессе расчета траектории в соответствии с известной процедурой Фаулера. По завершении полного цикла нагружения, равного 720° п.к.в., производится вывод на печать всех среднеинтегральных и экстремальных значений гидромеханических характеристик, в том числе эпюры гидродинамических давлений, действующих со стороны смазочного слоя на кривошипную головку шатуна.

Результаты тестовых расчетов. Выполнены расчеты для шатунного подшипника двигателя Ruston&Hornsby 6 VEB-X МКШ, признанного эталонным в области УГД анализа. Имеются достоверные экспериментальные (полученные на двигателе и моделирующей установке) и многочисленные теоретические результаты расчета параметров движения шатунной шейки за цикл нагружения, а также гидромеханических характеристик этого подшипника в двух исполнениях: с кольцевой канавкой шириной 0,0127м и без нее. Геометрические параметры трибосопряжения приведены в табл. 1.

Таблица 1

Параметры трибосопряжения

Параметр	Размерность	Величина
Диаметральный зазор (номинальный)	мкм	165,0
Длина подшипника	м	0,127
Диаметр подшипника	м	0,203
Частота вращения шипа	мин”1	600

Рассчитывались гидромеханические характеристики абсолютно жесткого и упругоподатливого подшипников при граничных условиях Свифта-Штибера (СШ) и Якобсона-Флоберга-Ольсона (ЯФО). Во всех вариантах среднеинтегральная (расчетная) температура смазочного слоя принималась равной 100 °C (табл. 2). Расчеты выполнены при помощи программного комплекса «Упругость II» [9].

Из представленных данных видно хорошее соответствие полученных результатов с экспериментальными, а также полученными другими исследователями. Учитывая, что двигатель Ruston&Hornsby 6 VEB-X МКШ является малонагруженным, а его шатун сравнительно жестким, влияние упругих деформаций на экстремальные гидромеханические характеристики не столь значительно: 30 % - для граничных условий Свифта-Штибера и 34 % - для граничных условий ЯФО. Однако снижение минимальной толщины смазочного слоя в характерных положениях кривошипа (280° и 640° поворота коленчатого вала) существенно больше. Аналогичным образом ве-^ Вестник ЮУрГУ, № 33, 2009

дет себя и максимальное гидродинамическое давление в диапазонах, когда поле давлений действует в направлении наибольшей податливости шатуна.

Таблица 2

Модель	inf/zmin,MKM	ЗиР^тах.МПа
Модель «абсолютно жесткого» подшипника
Граничные условия СШ	4,2	35,09
Граничные условия ЯФО	4,1	35,66
Модель податливого подшипника
Граничные условия СШ	3,39	34,82
Граничные условия ЯФО	3,27	36,02
Экспериментальные результаты
Эксперимент [4]	3,33	32,50
Результаты других исследований
Упругий подшипник [10]	3,38	33,92
Упругий подшипник [11]	3,15	35,22

Представленная работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации в рамках Федеральной целевой программы «Научные и научнопедагогические кадры инновационной России на 2009-2013 годы» и Российского фонда фундаментальных исследований (проект 07-08-05 54).