Алгоритм решения задачи Шоуолтера -Сидорова для моделей леонтьевского типа
Автор: Келлер Алевтина Викторовна
Статья в выпуске: 4 (221), 2011 года.
Бесплатный доступ
Работа посвящена задаче Шоуолтера - Сидорова для моделей леон-тьевского типа. Представлен алгоритм решения этой задачи в виде блок-схемы программы, написанной на языке С+-. Представлены результаты вычислительных экспериментов для моделей леонтьевского типа.
Задача шоуолтера - сидорова, модели леонтьевского типа, алгоритм программы
Короткий адрес: https://sciup.org/147159125
IDR: 147159125 | УДК: 517.9
Текст научной статьи Алгоритм решения задачи Шоуолтера -Сидорова для моделей леонтьевского типа
Пусть L и M - квадратные матрицы порядка п, причем detL = 0. Будем рассматривать задачу Шоуолтера - Сидорова
[(aL-M)4L]P(t1(O)-«o) = O (0.1)
для вырожденной системы уравнений
Lu = Mu + f, (0.2)
где Ra(M) = {aL — М)~х L - правая Z-резольвента матрицы М, в отличие от ее левой L -резольвенты L^ (М) — L(aL - M'j^1, а / : [0,Т] —> К" - некоторая вектор-функция (здесь и далее терминологию см. в [1]. Одним из важных случаев системы (0.2) является динамическая балансовая система В.В. Леонтьева «затраты-выпуск» с учетом запасов (см. в [2]), поэтому в [3] было предложено такие системы уравнений называть «системами леонтьевского типа». При решении конкретных прикладных задач, сводящихся к системам леонтьевского типа, полученную модель будем называть моделью леонтьевского типа.
В [3] предложен алгоритм решения задачи Коши к(0) = по для системы леонтьевского типа (0.2). Несмотря на высокое качество программного продукта, основным недостатком этого алгоритма является ограничение на размер матриц, входящих в состав системы. Это ограничение обусловлено необходимостью построения множества допустимых начальных значений, понимаемых как фазовое пространство системы (0.2), и наложением условия согласования f(t) с начальным значением «о- Рассмотрение в качестве начальных условий
(0.1) позволит избежать этих трудностей. Именно поэтому начальные условия Шоуолтера - Сидорова рассматирваются при исследовании различных прикладных задач [4-6]. Основная цель данной статьи - построение алгоритма численного решения задачи Шоуолтера - Сидорова в виде блок-схемы. Статья состоит из введения и трех параграфов. В первом приводится теорема о численном решении задачи Шоуолтера - Сидорова и основных этапах алгоритма, во втором - блок-схема алгоритма, в третьем - результаты численных экспериментов для двух моделей леонтьевского типа.
1. Численное решение задачи Шоуолтера - Сидорова
Пусть Ьи М - квадратные матрицы порядка п, причем detL = 0. Следуя [7], гл. XII, п.2, пучок матриц pL — М назовем (Т,р)-регулярным, если существует число A G С такое, что det(XL-M) 7^ 0 и оо - полюс порядка р Е NU{0}. Заметим, что условие (Z,/^-регулярности пучка матриц эквивалентно условию (£,р)-регулярности матрицы М [8]. Решением системы (0.2) называется вектор-функция uq Е С1 ((0; Т); R") OC([0;T];R") , удовлетворяющая уравнениям системы. Решение системы (0.2) называется решением задачи (0.1), (0.2), если оно вдобавок удовлетворяет условию (0.1). Имеет место
Теорема 1. [[1], гл.4] Пусть матрица М (L,p)-регулярна, вектор-функция f : [0,Т] —> Г такова, что (L^M))pf Е С ([0; Т]; Rn), а П- (L^ (М))р f Е С”+1((0;Т);Г) О С'р ([0; Т]; R"). Тогда при любом ио Е R” существует единственное решение задачи (0.1), (0.2), которое к тому же имеет вид
Р
= н^1 (I - Q) ^ (t) + иъио + / Rt^Qf (s) ds. (1.1)
Здесь
= [Ri (М) eptdp, Rt = ±-hpL- МУ e^dp, Q = ~ [ 1% (М) dp 2кг Jy 2кг Jy 2кг Jy контур ”f = {р Е С : \р\ = г > а} .
Контурные интегралы не очень удобны в численных расчетах, поэтому в [3] предложен другой подход, основанный на аппроксимациях типа Уиддера-Поста [[1], гл. 2]. Именно справедлива
Теорема 2.
положим
Пусть матрица М (L,p)-регулярна, зафиксируя Т Е Re +,t Е (0,T),fc€N
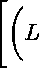
t
k(p + 1)
_! й(р+Ц L
Qk=[kLi(M)]p+\
Тогда при любых izq G R" u вектор-функции f E Cp+1 ((0;T) ;Rn) П Cp ([0;T] ;Rn) прибли женное решение задачи (0.1) и (0.2) имеет вид р ft uk W = - У 1 (^ - № W + ^о + / R^Qkf (s) ds. (1.2)
,=о Jo
При построении алгоритма принимается допущение о том, что detM ^ 0. Оно не ограничивает общности предыдущих рассуждений. Действительно, при условии регулярности пучка pL — М можно сделать замену и = е^и в уравнении (0.2) и перейти к уравнению
Lv = (M- XL)v + e~At(y + Ви)
(1-3)
того же вида, что и (0.2), но det(M — XL) ^ О.Обратный переход от решений системы (1.3) к решениям системы (0.2) очевиден.
2. Блок-схема алгоритма численного решениязадачи Шоуолтера - Сидорова
Алгоритм численного решения реализован на языке C++ [9]. Он является современным языком программирования, позволяющим удобно писать эффективные программы. Большинство известных компиляторов других языков значительно проигрывают в скорости выполнения программ известным компиляторам C++. Приведем блок-схему алгоритма (см. рисунок).
Поскольку ап = detL, то коэффициент ai — (—1)^“^ ^ Д^_г 0 —0,п), ^п-/” опРе^елите“ Г = 1
ли, получаемые из определителя матрицы L путем замены п — 1 столбцов соответствующими столбцами матрицы М, г - порядковый номер определителя, q < rankL. Итак, det(pL — М) = aqpq + ag-ip9^1 + ... + а^р + ао, где q = degdet(pL — М) < rankL. Поэтому, если взять число а Е R таким, что а > max <
1,1а?1
52 n)/-0 / ,
то det(aL — M) ^0,и, значит, существует матрица (aL — М)^1. Далее, считая, что матрица М обратима, представим det(pL — М) = detMdet(pM~1 L — I). Зная, что порядок полюса в точке оо резольвенты (pl — M~1L)~1 равен нулю, легко найти, что порядок полюса L- резольвенты матрицы М в точке оо равен п — q. Итак, числа а и р — п — q найдены.
Далее будем находить значение к, с которого можно начинать считать приближенные проекторы, получим, что мы не сможем оказаться даже вблизи точки L-спектра оператора М при к = max {ki; к^}, где t Е [0,1]
^i > lfl
Далее вычисляются матрицы, входящие в состав (1.2), при численном интегрировании применяется квадратурная формула Гаусса, вычислется прилиженное решение задачи (0.1), (0.2).
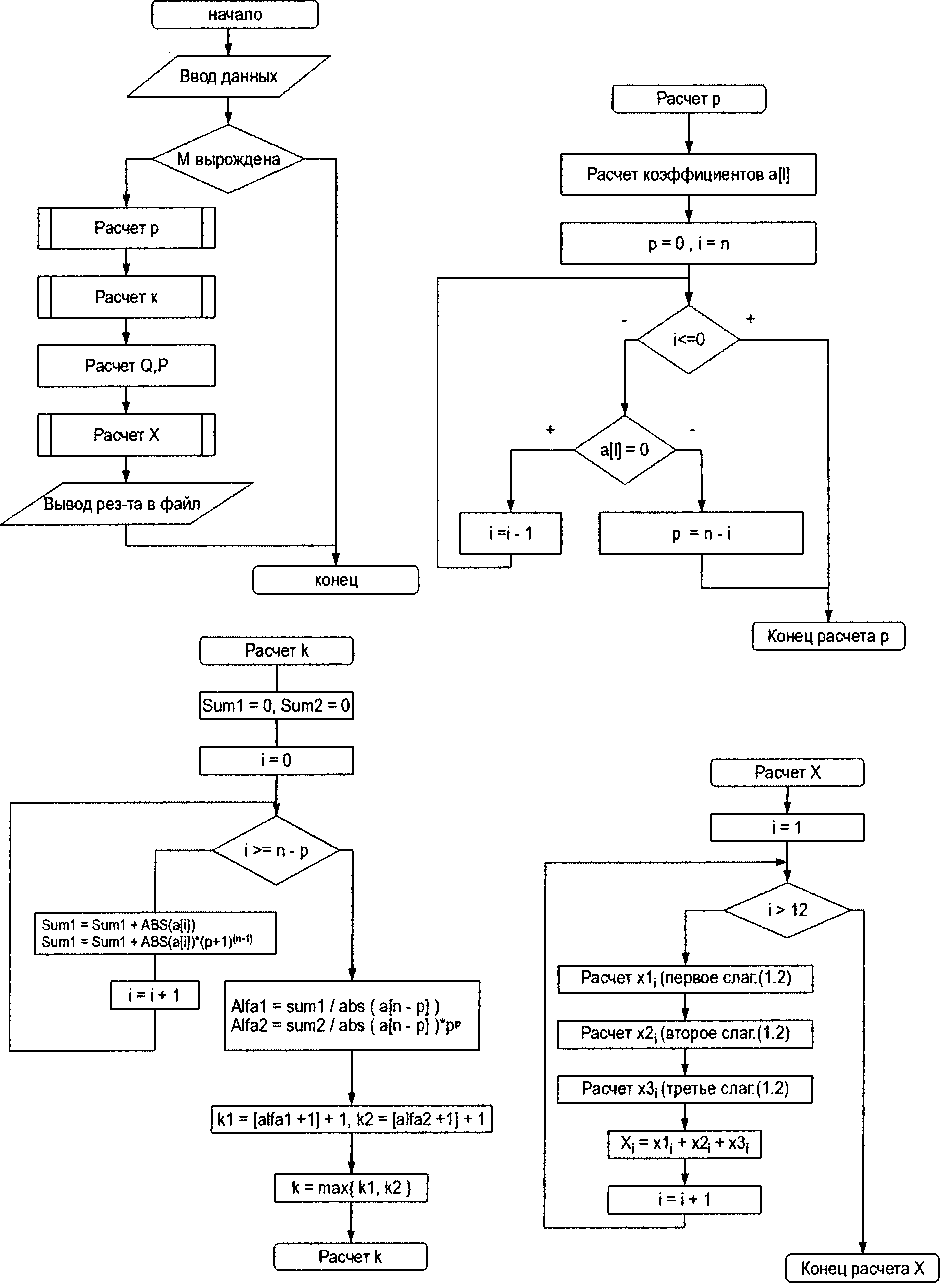
Блок-схема алгоритма
3. Примеры моделей леонтьевского типа
Пример 3.1. Рассмотрим модель модернизированного устройства, приведенную в [10]. Редуцируя ее к модели леонтьевского типа, как предложено в [11], получим
/1 0 0\ /—44 0 0 \ /15sin27rt 00\
(3.1)
0 1 0 р = -117 -16 0 р + 00 0,
\0 0 0/ \ 0 1 -1/ \ 0 00/ где z = (xi(t)iX2(t),y(t)), zq = (0,0,0). В табл. 1 приведено численное решение системы (3-1).
Таблица 1
Приближенное решение задачи динамического измерения
|
t |
«1 |
®2 |
У |
|
0 |
0 |
0 |
0 |
|
1/12 |
-0,013771 |
0,029312 |
0,029312 |
|
1/6 |
-0,066267 |
0,237938 |
0,237938 |
|
1/4 |
-0,146596 |
0,674819 |
0,674819 |
|
1/3 |
-0,233314 |
1,253692 |
1,253692 |
|
5/12 |
-0,303189 |
1,827654 |
1,827654 |
|
1/2 |
-0,337497 |
2,245077 |
2,245508 |
|
7/12 |
-0,327046 |
2,394683 |
2,394683 |
|
2/3 |
-0,274635 |
2,236538 |
2,236538 |
|
3/4 |
-0,194309 |
1,813055 |
1,813055 |
|
5/6 |
-0,107590 |
1,237718 |
1,237718 |
|
11/12 |
-0,037715 |
0,664689 |
0,664689 |
|
1 |
-0,003407 |
0,247513 |
0,247513 |
В [12] представлено точное решение системы (3.1), расхождения в точном и приближенном решении порядка не более 10-3.
Пример 3.2. Для небольшого предприятия составлена модель леонтьевского типа. Порядок составления модели для экономических приложений описан в [13]
|
/0,492 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
о\ |
|
|
0 |
0,467 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0,319 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
1,667 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
17,142 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
L = |
0 |
0 |
0 |
0 |
0 |
7,667 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1,25 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
66,47 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
9,091 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
< 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
°/ |
|
/ 0,96 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 А |
|
|
-0,38 |
0,97 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
-0,08 |
0 |
0,95 |
0 |
0 |
-0,5 |
0 |
0 |
0 |
0 |
0 |
|
|
-0,04 |
0 |
0 |
0,93 |
0 |
0 |
0 |
-0,01 |
0 |
0 |
0 |
|
|
-0,05 |
0 |
0 |
0 |
0,86 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
м = |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
-0,99 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
|
-0,02 |
-0,02 |
-0,03 |
-0,33 |
-0,11 |
-0,03 |
-0,01 |
-0,03 |
0,95 |
1 50 |
1 200 |
|
|
-0,19 |
-0,03 |
-0,06 |
-0,13 |
-0,11 |
-0,33 |
-0,25 |
-0,66 |
0 |
1 |
0 |
|
|
к 0 |
-0,07 |
-0,96 |
-0,1 |
-0,1 |
-0,5 |
-0,1 |
0 |
0 |
0 |
1 / |
F = coZ(500, 398, 103,5, 500, 50, 300, 900, 309, 0, 0, 0).
X0 = coZ(52, 600, 313,5, 90, 87,5, 300, 1200, 309, ПО, 880, 2167,5).
Решение задачи Шоуолтера - Сидорова представим в табл. 2.
Численное решение задачи Шоуолтера - Сидорова
Таблица 2
|
t |
«1 |
«2 |
ОД |
«4 |
ОД |
«6 |
«7 |
ОД |
1*9 |
«ю |
«п |
|
0 |
52 |
600 |
313,5 |
90 |
87,5 |
300 |
1200 |
309 |
ПО |
880 |
2167,5 |
|
1 12 |
179,1 |
807,38 |
393,4 |
94,2 |
88,1 |
309,2 |
1340,5 |
301,8 |
109,8 |
951,6 |
2592,1 |
|
302,6 |
1024,6 |
482,7 |
98,45 |
88,7 |
317,5 |
1474,2 |
302,5 |
109,5 |
1031,1 |
2965,0 |
|
|
448,1 |
1274,2 |
592,7 |
102,4 |
89,2 |
325,9 |
1617,1 |
303,3 |
109,1 |
1119,5 |
3388,3 |
|
|
619,3 |
1560,8 |
728,5 |
106,4 |
89,7 |
334,4 |
1769,8 |
304,0 |
108,4 |
1217,9 |
3870,8 |
|
|
820,8 |
1889,3 |
896,8 |
110,1 |
90,1 |
343,0 |
1933,0 |
304,7 |
107,6 |
1328,1 |
4422,6 |
|
|
1057,9 |
2265,4 |
1105,9 |
113,6 |
90,5 |
351,8 |
2107,4 |
305,5 |
106,5 |
1457,1 |
5056,3 |
|
|
1337,2 |
2696,1 |
1366,5 |
116,8 |
90,9 |
360,6 |
2294,4 |
306,3 |
105,3 |
1591,1 |
5787,1 |
|
|
1666,0 |
3188,1 |
1692,0 |
119,5 |
91,2 |
369,6 |
2493,1 |
307,1 |
103,7 |
1748,2 |
6632,7 |
|
|
2053,1 |
3749,5 |
2099,6 |
121,7 |
91,3 |
378,7 |
2706,1 |
307,8 |
101,6 |
1927,8 |
7617,7 |
|
|
1 |
2508,8 |
4389,1 |
2610,8 |
123,1 |
91,4 |
388,0 |
2933,6 |
308,6 |
99,3 |
2131,9 |
8766,8 |
|
11 12 |
3045,5 |
5116,7 |
3252,6 |
123,6 |
91,4 |
397,3 |
3177,0 |
309,3 |
96,4 |
2365,5 |
10115,5 |
|
1 |
3677,5 |
5943,0 |
4063,1 |
123,1 |
91,2 |
406,8 |
3437,1 |
310,1 |
92,9 |
2633,9 |
11705,0 |
Алгоритм эффективен при численном решении моделей леонтьевского типа, у которых размер входящих в них матриц более 10.
Список литературы Алгоритм решения задачи Шоуолтера -Сидорова для моделей леонтьевского типа
- Sviridyuk, G.A. Linear Sobolev Type Equations and Degenerate Semi-groups of Operators/G.A. Sviridyuk, V.E. Fedorov. -Utrecht; Boston; Köln; Tokyo: VSP, 2003.
- Леонтьев, B.B. Межотраслевая экономика/В.В. Леонтьев.-М.: Экономика, 1997.
- Свиридюк, Г.А. Численное решение систем уравнений леонтьевского типа/С.В. Брычев, Г.А. Свиридюк//Изв. вузов. Матем. -2003. -№ 8. -С. 46 -52.
- Загребина, С.А. О задаче Шоуолтера -Сидорова/С.А. Загребина//Изв. вузов. Математика. -2007. -№ 3. -С. 22 -28.
- Замышляева, A.A. Фазовые пространства одного класса линейных уравнений Соболевского типа высокого порядка/A.A. Замышляева//Вычислит, технологии. -2003. -Т. 8, № 3. -С. 45 -54.
- Манакова, H.A. Задача оптимального управления для уравнения Осколкова нелинейной фильтрации/H.A. Манакова//Дифференциальные уравнения. -2007. -Т. 43, № 9. -С. 1185 -1192.
- Гантмахер, Ф.Р. Теория матриц/Ф.Р. Гантмахер. -4-е изд. -М.: Наука, 1988.
- Келлер, A.B. Системы леонтьевского типа: классы задач с начальным условием Шоуолтера-Сидорова и численные решения/A.B. Келлер//Изв. Иркут. гос. ун-та, Серия «Математика». -2009. -Т. 2. -С. 30 -43.
- Showolter -Sidorov problem (shosid problem): свидетельство 2010616865/Келлер A.B.(RU); правообладатель ГОУ ВПО «Южно-Уральский государственный университет». -210615137; заявл. 16.08.2010; зарегестр. 14.10.2010, Реестр программ для ЭВМ.
- Бизяев, М.Н. Динамические модели и алгоритмы восстановления динамически искаженных сигналов измерительных систем в скользящем режиме: дис.... канд. тех. наук/М.Н. Бизяев. -Челябинск: ЮУрГУ, 2004.
- Шестаков, А.Л. Новый подход к измерению динамически искаженных сигналов/А.Л. Шестаков, Г.А. Свиридюк//Вестн. ЮУрГУ, сер «Мат. моделирование и программмирование». -2010. -№ 16(192), Вып. 5. -С. 116 -120.
- Келлер, A.B. Свойство регуляризуемости и численное решение задачи динамического измерения/A.B. Келлер, Е.И. Назарова//Вестн. ЮУрГУ, сер «Математическое моделирование и программмирование». -2010. -№ 16(192), Вып. 5. -С. 32 -38.
- Келлер, A.B. Алгоритм численного решения задачи Шоуолтера -Сидорова для систем леонтьевского типа/A.B. Келлер//Методы оптимизации и их приложения: труды XIV Байкальской школы-семинара, Иркутск -Северобайкальск. -2008. -С. 343 -350.


