Алгоритм совместного решения уравнений тепломассопереноса и уравнений электромагнитного поля при сушке СВЧ-излучением

DOI:

Сушка материалов электромагнитным излучением является важным компонентом целого ряда современных технологий. Она применяется для обезвоживания пищевых продуктов и сельскохозяйственного сырья, для сушки древесины и строительных материалов, в дорожном строи- тельстве, при разработке горных пород и мерзлых грунтов, в горнодобывающей и нефтегазодобывающей промышленности, для создания экологически безопасных и энергоэффективных технологий в медицине, химической, электронной, текстильной, полиграфической, резиновой и целлюлозно-бумажной промышленности, в установках по созданию микроклимата в помещениях (регенерация материалов, используемых для поглощения водяного пара из воздуха). Математическому моделированию процесса электромагнитной сушки уделяется большое внимание в литературе. Для анализа этого вида сушки применяют как аналитические методы [2; 12; 15], так и численные [13; 14]. Большей частью применяется подход, когда плотность внутренних источников тепла, обусловленных поглощением электромагнитного излучения, является наперед заданной [2]. В тех же случаях, когда учитывается взаимосвязь электромагнитных процессов и процессов тепломассопереноса, для численного анализа используются коммерческие пакеты вычислительных программ, без детального указания того, как осуществляется согласованная работа пакетов [14]. Исправляя это положение, в настоящей статье мы подробно излагаем разработанный и опробованный авторами численный алгоритм, позволяющий находить совместные решения для уравнений тепломассопереноса и уравнений электромагнитного поля. Можно говорить, не изменяя существа проблемы, что этот алгоритм позволяет учитывать электромагнитную неоднородность среды, вызванную зависимостью диэлектрической проницаемости материала от температуры и влагосодержания, или что в рамках этого алгоритма учитывается обратное влияние распределений температуры и влагосодержания в некоторый момент времени на распределение поглощаемой электромагнитной энергии в тот же самый момент.

В работе исследуется электромагнитная сушка образца с плоской геометрией (рис. 1). Толщину пластины d примем малой по сравнению с ее размерами в направлениях, перпендикулярных оси x , а интенсивности тепло- и массообмена поверхности пластины x = 0 с набегающим потоком воздуха будем считать зависящими только от времени, но не от координат. При этих условиях можно поставить задачу об исследовании электромагнитных процессов и процессов распространения тепла и влаги в одномерном приближении . Следовательно, будем изучать ситуацию, когда все функции, характеризующие процесс, – распределения температуры Т и влагосодержа-ния U , теплофизические характеристики материала, эквивалентная диэлектрическая проницаемость материала ~ , плотность электромагнитных потерь W , - зависят только от координаты x и времени τ.

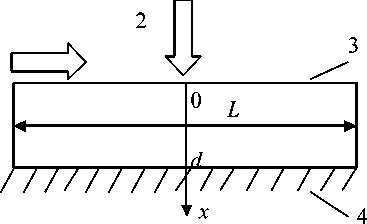
Рис. 1. Сушка плоского образца:

1 – воздушный поток; 2 – плоская электромагнитная волна; 3 – влажный образец; 4 – тепло- и влагоизоляция

Характеристики падающей волны будем считать заданными, а характеристики волны отраженной и волны внутри образца подлежат определению.

Алгоритм учета взаимного влияния электромагнитного поля и полей тепломассопереноса построен на решении следующих частных задач: а) расчет поля эквивалентной диэлектрической проницаемости материала ~(x, т) по известным полям T(x, т), U(x, т); б) расчет поля плотности электромагнитных потерь W(x, т) при известном поле ~(x, т); в) расчет полей T(x, т), U(x, т) при известном поле W(x, т). Рассмотрим последовательно эти частные задачи.

Объект сушки считается состоящим из твердой основы и воды, заполняющей капилляры и поры твердого компонента. Для решения электромагнитной задачи нужно знать зависимость эквивалентной диэлектрической проницаемости материала ~ от процентного соотношения между компонентами смеси, от частоты поля ω и температуры. Этому вопросу посвящена обширная литература. Для учета процентного соотношения применяют формулы смешения Зильберштей-на, Максвелла, Винера, Ландау – Лифшица, Максвелла – Вагнера, и другие [9; 10]. Мы будем использовать формулу Максвелла

~_~ U /( U + 1) ~ 1/( U + 1) ^{е — е} в          ' Ь т       ■

Здесь ~_в и ~_т - эквивалентные диэлектрические проницаемости воды и твердой основы, а величины U / ( U + 1) и 1 / ( U + 1) есть их массовые доли в смеси. Зависимость ~_в от частоты и температуры будем моделировать формулой Дебая

~ ев — е®

+ (ест

е J О + i ютр ).

В этой формуле е _ст - низкочастотная проницаемость; е_и - высокочастотная проницаемость; т _р - время релаксации. По данным измерений е_и = 5,5, а е _ст и т _р сильно зависят от температуры. Известные из литературы экспериментальные зависимости для этих величин [9] можно аппроксимировать следующими формулами:

е _ст — 186 - a ■ T ; т _р — т ₀ ■ exp ( E / kT )

Здесь а = 0,361 1/К; т ₀ = 6,47 х 10^-15 с; Е = 2,98 х 10^-20 Дж; к - постоянная Больцмана; Т -температура в К.

Эквивалентную диэлектрическую проницаемость твердой основы ~_т также полагаем известной функцией температуры и частоты. В итоге формулы (1)–(3) дают эквивалентную диэлектрическую проницаемость двухкомпонентного влажного материала ~ как функцию влагосодержа-ния U , температуры T и частоты ω.

Здесь мы рассмотрим алгоритм расчета плотности электромагнитных потерь и коэффициентов отражения и пропускания при известном распределении эквивалентной диэлектрической проницаемости по объему образца. Электромагнитное поле во всем пространстве будем считать гармоническим частоты ω, поэтому изложение будем вести на языке метода комплексных амплитуд. Комплексный характер векторов и скаляров никак не отмечается. Исходные соотношения электродинамики – материальные уравнения, первое и второе уравнения Максвелла для векторов поля Е , D , В и H , формулы для расчета плотности потока электромагнитной энергии S и плотности электромагнитных потерь W – имеют следующий вид [17]:

D — е0еE; B — р0рН; j — стE; е —е‘- iе"; р —р'- iр"; ст —ст'- iст";

rot H — i юе ₀ е E ;

rot E — - iюр 0рН;

е — е -

-^^l юе 0 J

-

i Ге" V

+

юе 0 J

5 = 1 Re (E x H*) W = ^(eos‘E\2 + W"|H).

Здесь j – плотность электрического тока; ε, μ, σ – соответственно диэлектрическая проницаемость, магнитная проницаемость и электропроводность среды; ~ = ~ ' - i ~" - эквивалентная диэлектрическая проницаемость материала (в дальнейшем слово «эквивалентная» мы чаще всего будем опускать). Вектор S и скаляр W , в отличие от других величин, являются вещественными.

Мы будем использовать также понятия комплексного показателя преломления среды n , волнового сопротивления вакуума Z ₀ и волнового числа k :

n = _xsp , Z о = V^ oАо , k = к о n , где к о = ®V^s o ^ o = ^ю/ ^с .

Все три среды, то есть сам слой и примыкающие к нему два полупространства, считаем немагнитными, поэтому для них ц ' = 1, ц '' = 0, и значит ц = 1, n = V~.

На рисунке 2 изображен плоский слой 2, разделяющий полупространства 1 и 3. Среды 1 и 3 - однородные и непоглощающие , поэтому их диэлектрические проницаемости ~ 1 , ~ ₃ и показатели преломления n 1 = ~ 1T_X, n ₃ = A~ 3 - вещественные числа. Среда 2 является и неоднородной , и поглощающей . Зависимость ее диэлектрической проницаемости от координат принимается в виде ~₂ = ~ = ~( x ) (неоднородность имеет слоистую структуру).

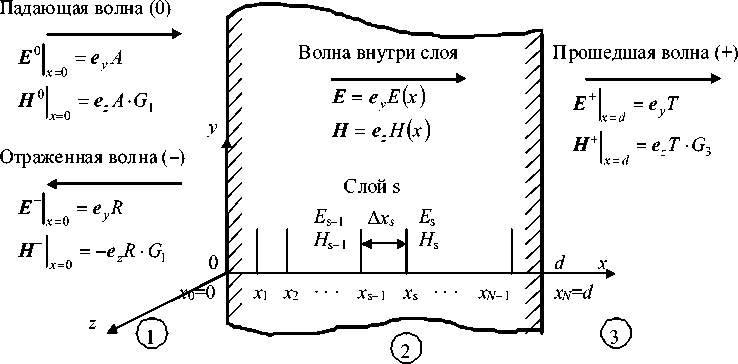
Рис. 2. К расчету электромагнитного поля внутри слоя методом характеристических матриц

Пусть из области 1 на левую границу области 2 в нормальном к ней направлении падает плоская гармоническая линейно поляризованная электромагнитная волна (волна ТЕМ -типа). Комплексные векторы этой волны, а также волны отраженной, прошедшей и волны внутри слоя, в декартовой системе координат имеют один и тот же вид

E = e y E ( x ) , H = e _Z H ( x ) ,

а дополнительные символы, позволяющие различать векторы этих четырех волн, показаны на рисунке 2 (используются символы 0, – и + соответственно для волны падающей, прошедшей и отраженной; для волны внутри слоя оставляем обозначения (7)).

Во всех трех средах уравнения Максвелла (5) для волн вида (7) будут выглядеть так:

dE(x)     .       , x dH(x)     . x / x

—— = - i юц о H ( x ), --- — = - i ms о s ( x ) E ( x ) .

dx                  dx

Тип этой системы двух обыкновенных дифференциальных уравнений первого порядка относительно двух неизвестных функций можно определить так: нормальная, линейная, однородная, с переменными коэффициентами .

В дальнейшем нас будут интересовать только однородные среды (неоднородный слой материала мы представим состоящим из тонких слоев однородных слоев). Для такого случая (~ = const) общее решение системы (8) известно [18]:

E ( x )	= F ( x ) ■	C 1	, F ( x ) =	cos k 0 nx in	sin k 0 nx in
H ( x )		C 2		--sin knnx 0 Z 0	cos k nx 0 Z 0

Здесь F ( x ) – фундаментальная матрица системы (8), а С ₁ и С ₂ – произвольные комплексные постоянные.

Исходя из формулы (9), построим электромагнитное поле как снаружи слоя (однородная среда без поглощения), так и внутри слоя (неоднородная среда с поглощением).

Рассмотрим сначала поле вне слоя. Пусть функция E ( x ) имеет на границах слоя некоторые значения А , R и T – соответственно для волны падающей, отраженной и прошедшей:

E 0 (0) = A ; E - (0) = R ; E ⁺ ( d ) = T .                           (10)

Отвечающие им значения функции H ( x ) можно найти из (9), если учесть, что при C 2 / C 1 = - i формулы (9) дают прямые , а при C 2 / C 1 = i - обратные волны (это устанавливается по виду вектора Пойнтинга для каждого из двух решений). Тогда будем иметь:

H0(0) = A ■ G1, H-(0) = -R ■ G1, H+ (d) = T ■ G3.                     (11)

Здесь G 1 = -^^Z 0 , G 3 = д/~ [z 0 - вещественные постоянные.

Рассмотрим теперь поле внутри слоя. Обратимся к вычислительному алгоритму работ [7; 8]. Представим область 2 состоящей из N слоев малой толщины, которые будем считать однородными . Сопоставим искомым функциям E ( x ), H ( x ) сеточные функции E_j , H_j и рассмотрим слой с произвольным номером s . В силу однородности слоя справедлива формула (9). Положим в ней сначала x = x_{s– 1}, E = E_{s– 1}, H = H_{s– 1}, а затем x = x_s , E = E_s , H = H_s ; исключая из получившихся уравнений С ₁ и С ₂, получим связь между компонентами поля на границах слоя с номером s :

				cos k 0 n s A xs in --- sin knn A x„ 0 s s Z 0	iZ --0 sin k 0 n s A xs ns cos k 0 ns A xs
E s H s	= Ms ■	E s - 1 H s - 1	, M s =			(12) .

Здесь n s = _Л/~ - комплексный показатель преломления слоя s .

Пользуясь рекуррентной связью, даваемой формулой (12), получим, что связь между компонентами электромагнитного поля на левой границе первого слоя и правой границе слоя с произвольным номером j будет иметь следующий вид:

E j H j

= Kj-

E0H0 ,

s = j

K j = n M s =

s=1

m1j1 m2j1

m1j2 m2j2

⁽ j = 1, " ) .

Квадратную матрицу второго порядка K j = ^ ₉ называют характеристической матрицей ( матрицей Коши ) неоднородного слоя. Она представляет собой произведение j матриц вида (12) и связывает компоненты поля при x = 0 и x = x_j (левая граница первого слоя и правая граница слоя j ).

В качестве следующего шага проведем «сшивание» построенных решений на границах неоднородного слоя (рис. 2). Формулы (10), (11) дают предельные значения компонент поля при подходе к границам слоя снаружи , а величины Е ₀, H ₀, Е_N , H_N есть предельные значения компонент при подходе к этим границам изнутри . Перечисленные компоненты поля являются касательными к границе, поэтому они должны изменяться непрерывно . Это приводит к следующим равенствам:

A + R = E 0 ; G i ( A - R ) = H 0 ; T = E n ; G 3 T = H n .

Величины Е ₀, H ₀, Е_N , H_N , кроме формулы (14), связаны еще формулой (13) при j = N :

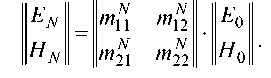
HN

Рассматривая совместно (14) и (15), найдем амплитудный коэффициент отражения r = R / A :

G 1 ( m N G ₃ - m 22 ) + m N G ₃ - m N

G 1 ( m N G ₃ - m 22 ) - m N G ₃ + m N ^.

Рассмотрим теперь способ вычисления средней по времени плотности электромагнитных потерь. Если магнитных потерь нет, то, согласно второй из формул (6),

W = - ( roe о / 2) • | E |² • Im e .

При конечно-разностном подходе для слоя j на рисунке 2 имеем

Wj = -(roe0/2) • E |2 ■ Im ej-.

Здесь величину e , так же как и значение компоненты Е , будем брать на правой границе слоя с номером j . Теперь нужно найти Е_j . Из (13) и (14) получим:

E j H j

m1j1 m1j2 m2j1 m2j2

E0H0

E ₀ = A + R = A (1 + r ); H ₀ = G 1 ( A - R ) = G 1 A (1 - r ) .

Здесь амплитудный коэффициент отражения r уже известен – он вычисляется по формуле (16). Рассматривая (18) и (19) совместно, найдем, что

E j = Am i'll + r ) + G 1 m j ₂(1 - r ) ] , откуда

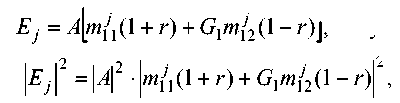
|Ej |² = l ^A l² • | m 1 ^j 1^{(1 +} r ) ^{+ G} 1 ^mj 2^{(1 -} r )| ,

и тогда по формуле (17)

W j = - ( roe ₀ /2) • Im ~ j ■ A |² • m j (1 + r ) + G 1 m j (1 - r )|2 .

Выразим здесь | A | ² через характеристики падающей волны при x = 0. Поскольку

S = 1 Re ( E х H *) , E = e _yE ( x ) , H = e _zH ( x ) , то

^S = ^{( e} y ^x e _z ) • ^{-Re [} E ^{( x} ) • H ^{( x} ) * ] = ^e x " j^{Re [} E ^{( x} ) • H ^{( x} ) * ^] , и тогда при x = 0 будем иметь

5 = e x S 0, где S ⁰ = 1| A ² G 1 .

Здесь S ₀ есть интенсивность падающей волны, которую мы считаем заданной. Выразим отсюда | А | 2 через S и подставим получившееся выражение в (20). Учитывая еще, что ше ₀/ G 1 = к ₀/ n ₁, получим такой результат:

к ₀ S ⁰ • Im ~ j     j                 j i2

W j =--- - m 1 j (1 + r ) + G₁ m₁ j ₂ (1 - r )

n ₁

Проведем расчет полей Т и U в пластине рисунка 1 при условии, что плотность внутренних источников тепла W (плотность электромагнитных потерь) является известной. Другие условия, при которых рассматривается задача, обсуждались ранее. Примем дополнительно, что теплофизические характеристики материала являются постоянными. Тогда начально-краевая задача для расчета поля температуры Т ( x , т ) и поля влагосодержания U ( x , т ) будет иметь следующий вид [11]:

9 T а 9 2 T      9 UА c Р0   = ХТГ + rYP0 V + W(x,т);

9т    9x2

9 U     9 ²U    _г9 ² T

= am + am$

9т       9x 2

Q (т) + r (1 - Y)- J (т) = Х9Т (0, т);

9 x

J(т) = a mP0

9 U

9x

(0,т)+8дT (0,т)

9x

9T (d, т) = 0;

9 x

T (x ,0) = T0 (x);

⁹ U ( d , т ) = 0;

9 x

U (x ,0)= U 0 (x);

Q(т) = aw [T(0, т)- Тв ] + a~[(T(0, т) + Ti )4 - (Тв + Ti )4 ];

J (т)=а m [P (T (0, т))-ф- P (Tв)!

q 173-T

P ( T ) = 6,03 - 10 ^{- 3} - exp- ⁷ ,³— T + T ₂ •

Здесь (22) и (23) – уравнения распространения тепла и влаги; (24) и (25) – краевые условия тепло- и массообмена на поверхности x = 0; (26) – краевые условия на поверхности x = d; (27) – начальные условия при τ = 0 (Т0(x) и U0(x) – некоторые заданные функции). Формула (28) определяет интенсивность теплообмена верхней границы пластины с потоком воздуха (учитывается теплообмен конвекцией и теплообмен излучением), а формула (29) – интенсивность массообме-на на этой границе. Интенсивность массообмена зависит от перепада давления водяного пара по толщине пограничного слоя (краевое условие Дальтона; в виде (29) оно впервые использовано в работе авторов [4]). В этих уравнениях: c, р0, y, X, am, 5 - теплофизические характеристики материала (удельная теплоемкость, плотность в сухом состоянии, критерий испарения, коэффициент теплопроводности, коэффициент диффузии влаги, относительный коэффициент термодиффузии вла- ги); r - удельная теплота парообразования воды; Тв и ф - температура и влажность воздуха за пределами пограничного слоя; σ – постоянная Стефана – Больцмана; А – коэффициент теплового излучения; Р(Т) – функция Г.К. Филоненко, моделирующая зависимость относительного парциального давления насыщенного водяного пара от его температуры Т при общем нормальном давлении; Т1 = 273 ºС и Т2 = 238 ºС – постоянные; αw и αm – коэффициенты тепло- и массообмена поверхности образца с воздушной средой. При ламинарном состоянии пограничного слоя их можно рассчитать по формулам, полученным авторами в [4]:

а w = k w_Xb ; a m = MVv ; k w = 3-82с; k m = 2,54 '10 ^-^ V L           у L            M • С                  C • м

Здесь L – длина пластины в направлении движения воздушного потока, а V – его скорость.

Алгоритмы численного решения начально-краевых задач для уравнения диффузии изложены, например, в [1; 16]. Но в данном случае мы имеем систему двух связанных параболических уравнений. Численная схема для этого случая разработана авторами в [5]. В этой работе рассмотрен общий случай с переменными коэффициентами. Аппроксимация второй производной конечными разностями производится с помощью симметричной неявной схемы Кранка – Николсона с шеститочечным шаблоном, а получившиеся в результате аппроксимации системы линейных алгебраических уравнений трехдиагонального вида решаются методом прогонки. Авторами разработаны также вопросы тестирования вычислительной программы и организации текущей проверки ее работы с помощью законов сохранения энергии и вещества, а также численная схема для исследования двумерных задач с постоянными теплофизическими коэффициентами [6].

Рассмотрим теперь алгоритм совместного решения уравнений электромагнитного поля и уравнений тепломассопереноса при сушке плоского образца на рисунке 1. Блок-схема алгоритма изображена на рисунке 3.

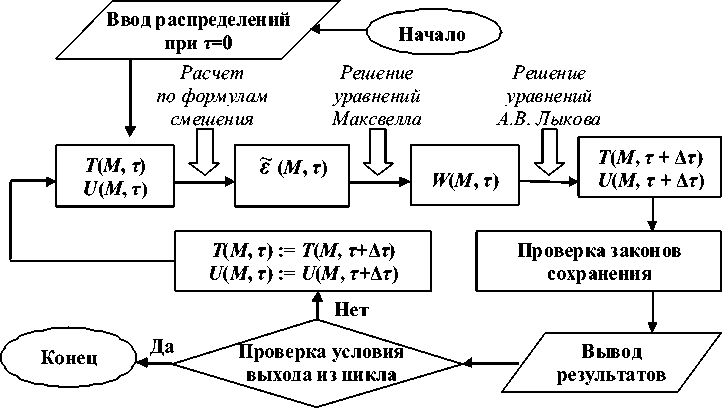
Рис. 3. Блок-схема для совместного исследования полей Т , U и W

После ввода начальных распределений температуры T(M, τ) и влагосодержания U(M, τ) по формулам смешения рассчитывается поле эквивалентной диэлектрической проницаемости ~(M, т). Затем при известном поле е(M, т) решается система уравнений Максвелла и находится поле электромагнитных потерь W(M, τ). После этого при известном поле W решает- ся система уравнений А.В. Лыкова и находятся поля Т и U в следующий, близкий к предыдущему момент времени.

На следующем шаге для проверки корректности работы программы осуществляется текущая проверка законов сохранения для электромагнитной энергии, для тепловой энергии и вещества. Далее проверяется условие выхода из цикла, и, если оно не выполнено, только что найденные распределения объявляются начальными и организуется новый цикл вычислений.

Предусмотрены также режимы тестирования вычислительной программы. Для этого используются аналитические решения системы уравнений электромагнитной сушки [3], которые авторам удалось найти для случая, когда т ^ ^ ( асимптотические решения ). Численные решения с течением времени должны выходить на них.

Материалом пластины является влажный цеолит . Теплофизические характеристики цеолита: y = 0,12; Р₀ = 1,1 • 10 3 кг/м³; § = 1,9 • 10^-3 1/°С ^ = 0,25 Вт/(м • °С); a m = 6,5 • 10^-7 м²/с; с = 1,1 • 10 3 Дж/(кг • °С). Диэлектрическая проницаемость цеолита в сухом состоянии ~_т моделировалась формулой Дебая с постоянными параметрами у = 5,3; е _ст = 11,0; т _р = 2,3 • 10^-11 с. Другие характеристики процесса: размеры пластины d = 0,02 м, L = 0,2 м; параметры воздушного потока Т _в = 20 ºС, V = 2,0 м/с, φ = 0,5; начальные распределения температуры и влагосодержа-ния Т ( x , 0) = 13,0 ºС = const = Т _м (температура мокрого термометра), U ( x , 0) = 0,2 = const; диэлектрическая проницаемость среды по обе стороны от пластины Е 1 = Е 3 = 1; интенсивность падающей волны S ⁰ = 0,5 Вт/см²; частота излучения f = 10 ГГц; коэффициент теплового излучения А = 0 (теплообмен излучением не учитывался).

На рисунке 4 показано распределение влагосодержания за все время сушки. Полное время сушки составляет приблизительно 48 мин, а переходные процессы продолжаются около 20 минут. После их окончания режим сушки приближенно можно считать квазистационарным . Он характеризуется стационарным температурным полем с температурой поверхности Т (0) = 56 °С, неизменной интенсивностью сушки J = 1,54 • 10^-3 кг/(м² • с) и неизменной скоростью сушки d U / д т = -4,2 • 10^-3 мин^-1. Электромагнитные коэффициенты отражения и поглощения в течение сушки изменяются незначительно и составляют R = 0,3 и Р = 0,7 соответственно (коэффициент пропускания I = 0). Распределение подведенной к пластине электромагнитной энергии в конце сушки имеет следующий вид: отражается 30 %; расходуется на испарение воды и на нагревание материала 48 и 10 % соответственно; теряется за счет теплообмена с воздушным потоком 12 %. Энергоемкость сушки (количество электромагнитной энергии, необходимой для удаления из материала 1 кг воды) оказывается равной 4,8 МДж/кг (с учетом отражения), что согласуется с результатами измерений: по данным [19], эта величина должна составлять 4 ÷ 6 МДж/кг.

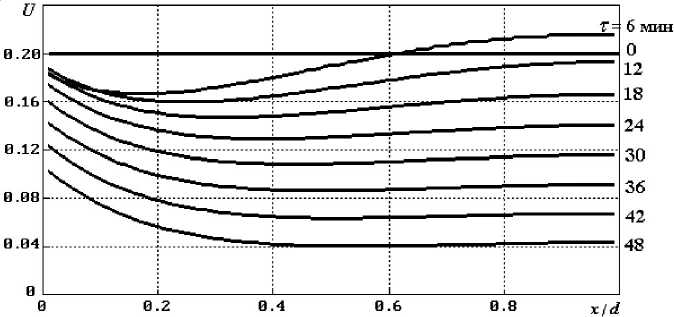
Рис. 4. Распределение влагосодержания U по толщине пластины в различные моменты времени τ при сушке цеолита

Разработана численная схема для совместного решения уравнений распространения тепла и влаги А.В. Лыкова и уравнений Максвелла. Она строится на основе двух алгоритмов: а) при заданном распределении диэлектрической проницаемости решается задача о расчете поля плотности электромагнитных потерь, коэффициентов отражения и пропускания; б) при заданном поле плотности электромагнитных потерь решается задача о расчете полей температуры и влагосо-держания. Роль связующего звена между этими двумя алгоритмами выполняет формула Дебая (она определяет зависимость диэлектрической проницаемости каждого из двух компонентов смеси, твердой основы и воды, от частоты и температуры) и формула смешения Максвелла (исходя из формул Дебая для твердой основы и воды, она определяет диэлектрическую проницаемость смеси этих компонентов как функцию частоты, температуры и влагосодержания). Проведен численный эксперимент (сушка влажного цеолита электромагнитным излучением СВЧ-диапазона), результаты которого находятся в хорошем согласии с имеющимися в литературе опытными данными.