Алгоритм статистической обработки результатов измерений участков лесных автомобильных дорог с помощью контрольно-измерительного комплекса

Проведение метрологических испытаний информационно-измерительного комплекса дорожной лаборатории требует разработки теоретических основ и методики их выполнения.

В качестве основного метода исследования точности принят метод сравнения результатов, полученных с его помощью, с аналогичны- ми результатами, полученными на основе геодезических измерений. При этом геодезические данные приняты за основные, поскольку они обладают наиболее высокой точностью.

Чистяков А.Г., Глазкова Е.В., 2014

Алгоритм статистической обработки результатов измерений участков лесных автомобильных дорог с помощью контрольноизмерительного комплекса представлен ниже.

1. Вычисляют среднее значение угла поворота а : cp

тории по закруглению, по данным которых

определяют среднее значение угла поворота

а cp

с погрешностью, не более m .

Соотношения (2-5) позволяют оценить

точность определения угла поворота, однако

они же являются полным и окончательным

n

? aлi аср =----- (1)

cp     n

2. Вычисляют среднюю квадратическую

погрешность одного определения а л :

m„ = ± ал

n n — 1

и среднего значения а cp

m acp

n 2 n

—

V

m ал

n

л

а О" cp

,

3. Строят доверительные интервалы

для

истинного угла поворота а по результатам ист одного i -го проезда лаборатория и по осред- ненным данным на n проездов:

а - — t i ma

а _ cp

—

tm аср

< а ист

< а ист

< а ш

< а сз

+ 1     ,

ma,

+ ta   , cp ,

где t - квантиль нормированного нормального распределения, соответствующий принятой вероятности Ф ( / ) .

4. Все результаты разделяют на четные и нечетные и вычисляют все статистики отдельно по четным и нечетным значениям. Аналогично необходимо образовать выборки из 1,4,7,10,…, затем из 2,5,8,11,…и 3,6,9,12,…,

значения а л (то есть отобрать из всех значе-

ний каждый третий результат, начиная с первого, затем со второго и затем с третьего) и повторить трижды вычисления всех статистик по 1/3 всех проездов. Аналогичным образом необходимо образовать 4 выборки численностью n /4 и вновь повторить все вычисления.

Результаты всех вычислений можно представить на графиках. Если на графике

провести горизонтальную прямую на уровне

та = т_л ( т_А cp    доп    доп

допустимое значение

погрешности та

cp

),

то на оси абсцисс можно

получить значение n , которое обеспечивает

определение а cp

с допустимой погрешно-

стью. Величина n определяет необходимое число челночных проездов дорожной лабора-

решением задачи.

• 4.    Для сравнения углов поворота, полученных с помощью дорожной лаборатории ( а_д ), и на основе геодезических измерений ( а_г ), на закруглении необходимо определить точки начало закругления (НЗ) и конец закругления (КЗ). Погрешности разбивки оси дороги на закруглении связаны с тем, что плавная круговая кривая заменяется хордами длиною S =10, 15, 20 м. Середины хорд отклоняются от круговой кривой на величину «стрелы» S

f = —, которая проявляет себя как погреш-8R ность разбивочных работ.

Допускаемые проектные отклонения от проектных размеров ширины покрытия равны: для асфальтобетонных покрытий ± 10 см и для цементобетонных ± 5 см.

Погрешности положения кромки, связанные с её загрязнением и разрушением при эксплуатации, оценивается величиной от 2-3 до 20-25 см [1-2]. В среднем она, по-видимому, не превышает 10-11 см.

Таким образом, суммарная величина случайного отклонения кромки покрытия от круговой кривой будет равна:

l     =± V6,5² + 8² + 11² =± 14 см.

сумм      ^,

Если погрешность l _м =± 14 см считать предельной, то средняя (квадратическая) будет равна l « ± 7 см.

• 5.    Погрешность угла поворота, измеренного с помощью дорожной лаборатории, можно охарактеризовать разностью:

А а = а — а ,            (6)

л г, где ал и аг - значения угла поворота, полученные лабораторией и геодезическим методом.

Вместе с тем, разность А а есть результат действия случайных погрешностей при измерениях а л и а г , то есть:

Аа=± V^l+^T,        (7)

Откуда погрешность измерения угла поворота с помощью дорожной лаборатории будет равна:

т _а = ±^Аа ² — т °_г           (8)

Погрешность измерения угла а теодолитом очень мало зависит от инструментальной погрешности и почти полностью определяется влиянием погрешностей положения точек НЗ и КЗ, а также отклонениями кромки покрытия на закруглении от идеальной круговой кривой. При этом отклонения кромки от указанной кривой влияют на точность измерения угла а также, как погрешность центрирования теодолита и наблюдаемых точек (сигналов).

Влияние погрешностей центрирования теодолита и сигналов на точность измерения угла в выражается формулой:

( Ь 1 1⁺

( t )

+

mp = ± Р вц    V2

l ²

+   '    . х b1 •b b2

,

I х ( b 2 + b 2 - 2 b 1 b 2 cos в )

где lc , lг - погрешности центрирования сигналов и теодолита; b1 , b2 - длины сторон, обра- зующих угол в .

Если lс = lг = l, b1 = b2 = b и Р< 15°, то mp^ = pl / b.

Так как а = 2 ф , то погрешность измерения угла а , обусловленная отклонением кромки покрытия от круговой кривой, будет равна:

m a = ± ² P l / ^b

• 6.    Рассмотрим влияние погрешностей определения положения точек НЗ и КЗ на кривой закругления на точность измерения угла а . Как показано в работе [3], влияние указанных погрешностей на точность измерения угла ф определяется формулой:

dl

”» =4 Ra-       ⁽¹¹⁾

где mф - погрешность измерения угла ф, обу- словленная погрешностями положения точек

НЗ и КЗ на закруглении; р = 3438 - радиан в минутах; l - предельное отклонение кромки покрытия от круговой кривой с вероятностью 0,68; d,a - расстояния; R - радиус круговой кривой.

Так как а = 2 ф , то:

2l m„ = ±2р— а1    FN Ra

Суммарное влияние погрешностей m ^ и m „ на точность измерения угла а будет равно:

2      « i 1 d m 2 = 4р2l2I — +--- аг         I b2 Ral

Подставляя значение m ^ в (12), получим:

А а ² - 4 р ² l ² х

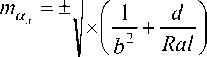
где Аа = а_л - а_г - разность значений угла поворота оси дороги, измеренных дорожной лабораторией и теодолитом; остальные обозначения прежние.

Формула (14) является окончательной рабочей. Она позволяет оценивать точность измерения углов поворота а оси дороги на закруглениях с помощью дорожной лаборатории. При этом разность Аа = ал - аг можно вычислять по значениям ал, полученным из одного, двух, трёх, четырёх и т.п. проездов лаборатории. Таким путём можно проследить, как изменяется погрешность m^ в зависимости от осреднения результатов (количества челночных проездов) и определять оптимальное число проездов.

Анализ данных, полученных по формуле (14), необходимо проводить совместно с анализом данных, полученных по формулам (2), (3), (4) и (5).

Важно ещё раз подчеркнуть, что изложенные выше теоретические основы метрологических испытаний лаборатории применимы только на круговой кривой.

• 7.    Измеряют длину кривой закругления с помощью дорожной лаборатории. Погрешность измерения длины кривой с помощью дорожной лаборатории можно охарактеризовать разностью:

А К = K л - К_г , (15) где К_л и К _г - длина кривой, измеренная с помощью лаборатории и геодезическим методом.

Одновременно разность А К равна:

^А К =± V m K л ⁺ m K _г (16)

В работах [3-4] показано, что погрешность измерения длины кривой, обусловленная неточным определением положения точек НЗ и КЗ, равна:

Rdl mKг =\ Т, (17)

где R - радиус круговой кривой; d , a - расстояния; l - предельное отклонение кромки покрытия от круговой кривой с вероятностью ~0,68.

Из формулы (17) видно, что для уменьшения погрешности измерения длины кривой точку N при определении начала и конца закругления следует выбирать как можно ближе к началу закругления, а расстояние MN = a d достаточно большим, чтобы отношение a мало отличалось от единицы. Эта рекомендация была уже сформулирована раньше без специального доказательства. Указанное, естественно, относится и к выбору точек M , N в конце закругления.

Тогда из (17) получим:

Rdl mK =+JAK---       (18)

^Kл             _d

Формула (18) является рабочей и позволяет оценивать точность определения длины кривой закругления с помощью дорожной лаборатории. Погрешность при измерении длины кривой с помощью дорожной лаборатории в основном определяется погрешностями положения точек НЗ и КЗ на закруглении. При проездах лаборатории «туда-обратно» по закруглению можно получить среднее значение длины кривой, которое будет в n раз точнее единичного определения этой длины для каждого проезда.