Алгоритм триангуляции, основанный на условии пустого выпуклого множества

DOI:

1.    Триангуляция конечного множества точек

Пусть R ⁿ — п -мерное евклидово пространство, в котором введен ортонормиро-ванный базис { е « } ”=1 . Через { , ) мы обозначаем скалярное произведение в R ⁿ . Пусть ж 1 , х ₂ ,..., х _п — соответствующие выбранному базису декартовы координаты.

Напомним, что к -мерным симплексом S = S(А ₀ , А 1 ,..., А ^ ) в R ⁿ называется выпуклая оболочка к + 1 точек А _г ,г = 0,...,к <  п , таких, что векторы А 1 — А ₀ , А 2 — — А д ,..., А ^ — А ₀ линейно независимы. Рассмотрим какой-либо п -мерный симплекс S . Пусть H ± (S ) обозначает открытое полупространство, определяемое плоскостью, проходящей через к -ю (п — 1) -мерную грань симплекса S , и содержащее (для H + (S ) ) или не содержащее (для H - (S ) ) симплекс S . Если из контекста ясно, о каком симплексе идет речь, мы будем опускать его обозначение в обозначениях этих полупространств. Также вместо обозначения симплекса мы равнозначно будем использовать набор его вершин.

Пусть {P _i } , г = 1,...,N , — некоторый набор P точек P _i Е R ” , таких, что любой симплекс в вершинах из { P i } является невырожденным. Триангуляцией Т заданного набора точек называется такой набор п -мерных симплексов S 1 ,...,S _m , что:

• 1)    каждая точка Pi заданного набора является вершиной одного из симплексов S Е Т;

• 2)    каждая вершина любого симплекса S Е Т является одной из точек Pi, г = = 1,...,N;

• 3)    внутренность пересечения любых двух симплексов пуста.

2.    Семейства выпуклых множеств

Один из первых алгоритмов триангуляции с использованием условия пустого шара был предложен Б.Н. Делоне в его работе [6] (перевод см. [1]). Это условие означает, что описанная сфера каждого симплекса триангуляции не содержит внутри себя точек заданного конечного множества. Триангуляции, для которых выполняется это условие, получили название триангуляции Делоне [4; 5]. Несложно показать, что при выполнении условия, что никакие п точек из Р не лежат на одной гиперплоскости и никакие п + 1 точек не лежат на одной (п — 1) -мерной сфере, триангуляция Делоне существует и единственна. С другой стороны, для конечного множества точек общего положения { P i } , г = 1,...,N , число различных триангуляций этого множества растет с ростом N порядка c ^N (см., например, работу [3] и цитируемую там литературу). Эти факты позволяют поставить задачу о выделении в классе всех триангуляций заданного конечного множества некоторого естественного подкласса, который бы включал в себя классическую триангуляцию Делоне в качестве частного случая.

Практически все алгоритмы построения триангуляции Делоне включают в себя процедуру проверки условия пустой сферы на определенных этапах алгоритма. Хороший обзор алгоритмов имеется в работе [5]. В настоящей статье мы тоже сосредоточимся на подобной процедуре, заменив условие пустой сферы условием пустого выпуклого множества. Дадим соответствующие определения.

Рассмотрим в R ” семейство Ф = Ф _а , а Е А , выпуклых компактных множеств с непустой внутренностью. Пусть S произвольный невырожденный симплекс. Определим описанное множество B(S ) Е Ф (если оно существует) из данного семейства как множество, чья граница содержит вершины симплекса (а значит, содержит весь симплекс в силу выпуклости).

Определение 1. Рассмотрим произвольную триангуляцию конечного множества точек P . Будем говорить, что эта триангуляция является Ф -триангуляцией, если для любого симплекса S этой триангуляции внутренность множества B(S ) не содержит вершин других симплексов.

Заметим, что если семейство Ф представляет собой семейство всех шаров в R ” , то вышеприведенное определение совпадает с определением триангуляции Делоне. В работе [2] было доказано существование ^ -триангуляции конечного множества точек при условии, что семейство Ф обладает следующим свойством: для любого невырожденного симплекса S в семействе Ф = Ф _а ,а Е А , существует, и притом только одно, описанное множество B(S ) .

В дальнейшем мы будем предполагать, что это условие на семейство выпуклых множеств выполненным.

Теорема 1. Если семейство выпуклых множеств Ф = Ф _а , а Е Л , обладает вышеприведенным свойством, то описанные множества симплексов обладают следующими свойствами:

• 1)    множество В(S) однозначно определяется любым симплексом с вершинами на его границе;

• 2)    если для двух невырожденных симплексов S1, S2 выполнено B(S1) = В(S2) и пересечение В(S1) ПB(S₂) не пусто, то персечение границ множеств B(S1), B(S2) представляет собой (п — 2) -мерную выпуклую поверхность, лежащую в некоторой гиперплоскости;

• 3)    если два симплекса S1 и S2 не пересекаются по внутренним точкам, имеют общую (п — 1)-мерную грань G и вершины симплексов А, В, не принадлежащие грани G, причем В(S1) не содержит внутри себя вершину В симплекса S2, то B(S2) не содержит внутри себя вершины А симплекса S1.

3.    Пример семейства Фа

Доказательство. Первое свойство непосредственно следует из условия на семейство Ф _а ,а Е Л . Второе свойство доказывается от противного. Если предположить, что пересечение dB(S 1 ) П ЭВ(S 2 ) не лежит ни в какой гиперплоскости, то найдется некоторый невырожденный симплекс S ‘ с вершинами на этом пересечении. Но тогда и В (S 1 ) и В(S 2 ) будут описанными множествами симплекса S ‘ , что противоречит условию единственности. Таким образом, пересечение ЭВ (S 1 ) П дВ(S 2 ) лежит в некоторой гиперплоскости. Выпуклость пересечения очевидно следует из выпуклости множеств В (S i ), В (S 2 ) (см. рис. 1).

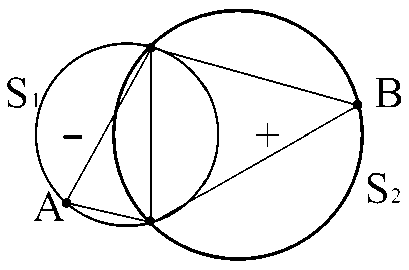
Рис. 1. К доказательству теоремы 1

Докажем третье свойство. Пусть П — гиперплоскость, содержащая пересечение дВ (S 1 ) П дВ (S 2 ) . Эта гиперплоскость разбивает каждое из В (S i ), г = 1, 2, на две выпуклые части В ± (S _i ) . Для определенности будем считать, что В Е В + (S ₂ ) и, следовательно, в силу того, что В не лежит внутри В (S 1 ) , выполнено В Е B + (S 1 ) . Тогда В + (S 1 ) С В + (S ₂ ), В - (S 2 ) С В - (S 1 ) . Если предположить, что точка А лежит внутри В (S 2 ) , то получим, что А Е B ^- (S ₂ ) . Поскольку эта точка лежит на границе B(S 1 ) , то заключаем, что В - (S 1 ) С В - (S 2 ) . Но это противоречит вложению В ^- (S ₂ ) С В - (S 1 ) . Следовательно, А не может лежать внутри B(S ₂ ) . Теорема доказана полностью.

Заметим, что в общем случае указать способ построения В(S ) для произвольного симплекса S , а также способ проверки условия пустого выпуклого множества из Ф _а представляет собой сложную задачу. Однако мы укажем целую серию семейств Ф _а , для которых это сделать удается.

Рассмотрим произвольную строго выпуклую вниз гладкую функцию х _п+1 = Ф(х) , определенную во всем пространстве R ” и такую, что

Ф(х)

и

^ + то при X ^ то .

При выполнении этого условия пересечение графика функции Ф(х) с произвольной невертикальной плоскостью П представляет собой выпуклую компактную (п— 1) -мерную поверхность в R ^{n +1} . Положим для любых х G R ⁿ ,r > 0

Ф(х,г) = {у G R ” : Ф(у) <  Ф(х) + ^Ф(х), у — X^х) + г } .

В силу свойства (1) и выпуклости Ф(х) множества Ф(х,г) образуют семейство выпуклых компактных множеств. Покажем, что для всякого невырожденного симплекса S можно построить единственное описанное множество из этого семейства. Пусть также точки р ₀ ,...,р _п G R ” образуют произвольный невырожденный симплекс S . В пространстве R ^{n +1} построим набор точек Q _t = (p t , Ф(р г )), i = 0,...,п . Построим в пространстве R ^{n +1} плоскость П , проходящую через эти точки. Очевидно, что проекция пересечения этой плоскости с графиком функции Ф(х) представляет собой границу некоторого множества Р Ы(х,г) . При этом точка х — это единственная точка, в которой касательная к графику параллельна плоскости П . Существование и единственность такой точки следуют из выпуклости и гладкости функции Ф(х) .

Теперь обратимся к вопросу проверки условия пустоты множеств вида В(х,г) . С этой целью построим функцию Н (р ₀ , ...,р _п ) , зависящую от (п + 1) точек из R ” . Пусть точки р ₀ ,...,р „ G R ” образуют произвольный невырожденный симплекс. В пространстве R ^{n +1} построим набор точек Q _t = (р _г , Ф(р _г )), i = 0,...,п . Построим в пространстве R ^{n +1} плоскость П , проходящую через эти точки и еще вертикальную гиперплоскость П ‘ , проходящую через точки Q ₀ , ...,Q _{n- 1} . Ориентируем эти плоскости нормалями £ и ^' соответственно следующим образом. Нормаль £ для П направим вверх, то есть так, чтобы ( е _п+1 , £ ) >  0 (здесь е _п+1 — единичный вектор положительного направления оси Ох _п+1 ). Вектор £ ‘ выберем как внутренний вектор по отношению к симплексу S(р ₀ , ...,р _п ) . Такой выбор корректен, поскольку плоскость П ‘ проходит через грань этого симплекса, определяемую вершинами р ₀ ,...,р _п . В качестве значения функции Н(р ₀ ,...,р _п ) возьмем величину угла между нормалями £ и £ ‘ . В основе проверки условия пустоты лежит следующее утверждение.

Теорема 2. Пусть Р с R ” произвольное конечное множество. Зафиксируем произвольно р _г G Р, i = 0, ..., п— 1 и пусть П — гиперплоскость, проходящая через эти точки. Будем предполагать, что эти точки образуют невырожденный (п — 1) -мерный симплекс. Пусть Р ‘ с Р — та часть точек из Р , которые лежат по одну сторону от П . Если точка р _п G Р ‘ такова, что

Н (ро,...,рп) = minH (ро,...,рп-1,р), ер ‘ рер*

то множество В(S) , где S — симплекс с вершинами р ₀ ,...,р _п не содержит внутри себя точек из Р ‘ .

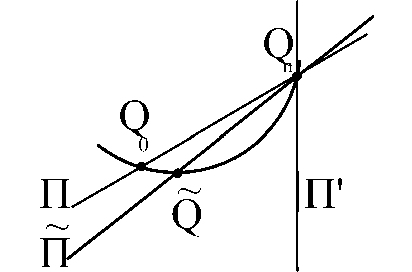
Рис. 2. К доказательству теоремы 2

Доказательство. Доказательство проведем от противного. Предположим, что найдется точка р Е Р ‘ , лежащая внутри B (S ) . Построим точку Q = (р, Ф(р ’ )) Е R ^{n +1} . В силу выпуклости функции Ф(х) точка Q лежит ниже гиперплоскости П (см. рис. 2).

Пусть П ‘ — вертикальная гиперплоскость в R ^{n +1} , проходящая через точки Q o ,...,Q n _-1 . Здесь точки Q ^ , г = 0, ...,п — 1 , построены также, как и в определении функции Н(р ₀ , ...,р_п) . Проведем через точки Q _o , ...,Q _{n- 1} ,Q гиперплоскость П . Поскольку точка Q лежит ниже плоскости П , то угол между плоскостями П и П ‘ больше, чем угол между плоскостями П и П ‘ . Последнее, как нетрудно видеть, означает, что

Н (р о , ...,Р п - 1 ,Р п ) >  Н (р о , ...,р п - 1 ,р).

Это противоречит выбору точки р _п . Таким образом, точка р не может лежать внутри B(S ) . Теорема доказана.

4.    Выпуклая оболочка и триангуляция

Для приведенного выше примера семейства выпуклых множеств триангуляция с условием пустых описанных множеств может быть построена универсальным алгоритмом, не зависящим от заданной выпуклой функции Ф(х) . Опишем соответствующую процедуру сведе´ ния построения триангуляции к построению выпуклой оболочки точек. Пусть Р С Rⁿ произвольное конечное множество точек, таких что никакие п + 1 из них не лежат в одной гиперплоскости и никакие п + 2 из них не лежат на границе одного множества семейства Ф(х,г) , построенного в предыдущем подразделе статьи. По множеству Р построим множество

Q = { (^ 1 , ..., Х п₊1 ) Е R ^{n +1} : (Х 1 ,..., Х п ) Е Р, Х п₊1 = Ф(х_ъ ..., Х п ) } .

Выпуклая оболочка conv(Q) этих точек представляет собой выпуклый многогранник в Rn+1. Рассмотрим те грани этого многогранника, чьи внешние нормали £ направлены «вниз», то есть для которых выполнено неравенство (£, еп+1) < 0. Проекция этих граней на плоскость хп+1 = 0 образует Ф-триангуляцию множества Р. Действительно, из того, что никакие п + 2 точек из Р не лежат на границе одного множества семейства Ф(х,г), следует, что выбранные грани выпуклой оболочки conv(Q) имеют ровно п + 1 вершину, то есть являются п-мерными симплексами в R7^1. Проекция симплекса тоже будет симплексом. В силу выбора граней проекции их не могут пересекаться по внутренним точкам. Таким образом, совокупность этих проекций образует триангуляцию множества Р. Стоит заметить, что точки множества Q не могут лежать ниже гиперплоскости, содержащей любую выбранную грань. Это простое следствие выпуклости многогранника conv(Q). А это влечет выполнение условия пустого описанного множества для семейства Ф(х, г).