Алгоритм управления механизмом с параллельной кинематической структурой

Приведен алгоритм управления механизмом с параллельной кинематической структурой, имеющим три степени свободы, обеспечивающий перемещение рабочего органа по заданной траектории. Представлены результаты математического моделирования.

Управление механизмом с параллельной кинематической структурой (рис. 1), математическая модель которого представлена в работе [1], имеет свои особенности. Так как в общем случае перемещение инструмента, закрепленного на фланце манипулятора, по заданной траектории осуществляется за счет одновременного изменения длин всех трех штанг, то при работе этого механизма в каждый момент времени должна выдерживаться согласованность скоростей двигателей, изменяющих длины штанг механизма. Нарушение согласованности между скоростями приведет к отклонению траектории движения инструмента от заданной.

Плоскость расположения верхних шарниров штанг   Плоскость расположения

\    д,^     / осей карданова шарнира

Рис. 1

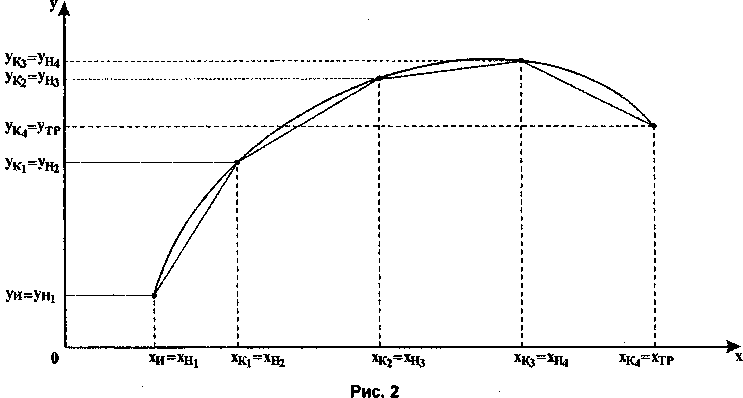
Пусть необходимо осуществить перемещение некоторой характерной точки механизма из исходного состояния, описываемого координатами (хи,уи,ги), в требуемое состояние с координатами (хТР, уТР, zTP) за время tTP по заданной траектории. В качестве характерной выберем точку К центра фланца манипулятора. На рис. 2 для примера показана некоторая траектория, при отработке которой изменяются только координаты х и у точки К.

При работе механизма заданная траектория должна разбиваться на участки, характер движения на которых описывается простыми зависимостями. В наиболее простом случае на участках могут быть реализованы линейные зависимости координат от некоторого параметра, в качестве которого может выступать время. Данная замена заданной траектории отрезками называется линейной интерполяцией траектории [2].

Применительно к управлению рассматриваемым механизмом в общем случае должна решаться задача трехмерной интерполяции траектории. В ходе решения этой задачи получается информация о координатах (хн.,ун. ,zH.) начальной и (хк.,ук. ,zK.) конечной точек i-ro линейного участка траектории, а также его длительности t,. На каждом линейном участке координаты должны изменяться в соответствие со следующими выражениями:

(xKi—xHi)'t         ,.х  (УК1-Ун|)'1              (zKj “ZHi)'^

Xj(t) =---‘ , ’  + хн., Yi(t) =---1     1    + yH. , Zj(t) =—^——^— + zH.,

■ ч                                                                                 " 4

где t - время от начала i-го линейного участка траектории. Очевидно, что (xHi,yHi,zH|) = =(хи,Уи>2и), (хн2,Ун2,2Н2) = (хК1,уК;,2К1) ИТ-Д-

Как показано в работе [1], формирование линейной траектории характерной точки рассматриваемого механизма требует изменять длины штанг по нелинейным законам. Следовательно, в общем случае скорость каждого из электродвигателей, изменяющих длины штанг, постоянно меняется.

При построении цифровых систем достаточно просто реализуется ступенчатое управление, при котором скорость электродвигателя в течение некоторого интервала времени является постоянной. Поэтому при управлении рассматриваемым механизмом необходимо решить задачу замены непрерывных требуемых нелинейных законов изменения длин штанг кусочно-линейными (рис. 3).

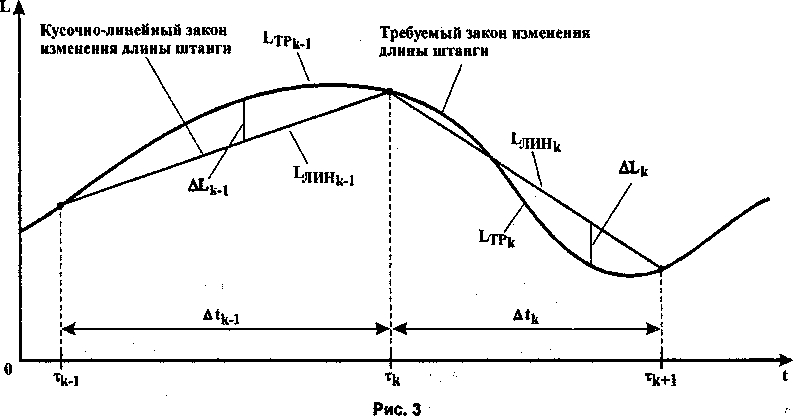
Решение данной задачи сводится к определению временных интервалов At^, на которых скорость вращения электродвигателя j -й штанги остается постоянной. На каждом из этих интервалов реальная длина штанги должна отличаться от требуемой на величину

^Щ-ДЬмах»                                                     О)

где j = 1,3 - номер штанги, AL^^ - заданное максимальное отклонение. Количество этих интервалов может быть разным для электродвигателей разных штанг, желательно, чтобы оно было

Смирнов В. А., Федоров В.Б.

минимальным. В моменты времени т^ осуществляется изменение скорости вращения электродвигателя j-й штанги.

Задача определения длительности At^ интервала сводится к нахождению максимума этой длительности при выполнении ограничений (1). Ниже предлагается вариант решения этой задачи.

Пусть требуемый закон изменения длины j-й штанги задается дискретной функцией LJ (tn ) = LJ (x(tn ), y(tn), z(tn )), где x(tn ), y(tn ), z(tn ) - координаты характерной точки механизма в моменты времени tn = п • At + tH, n = 0...N -1, At = ———, N - количество отсчетов дискретной N-l функции, tH, tK - моменты начала и окончания изменения длины штанги по заданному закону. Значение tK принимается за начальное для первого интервала постоянства скорости электродвигателя j-й штанги, т. е. т, = tK. Далее для моментов времени t,, i = 2,3... определяются отклоне ния

ALj(tu) =

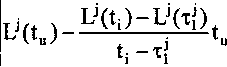
, где tu = г, + At,... tj_,

и сравниваются с ALM/XX (рис. 4).

Вычисления останавливают, как только текущее i-e значение AL^j(t_u) превысит AL_max . Значение 1_М будет являться конечным для первого интервала постоянства скорости электродвигателя j-й штанги и начальным для следующего, т. е. т^ = t^, и At^ = т^ - т(.

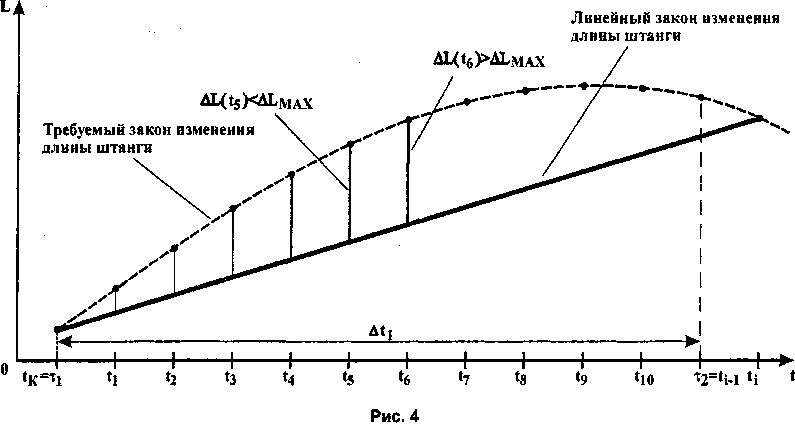
Аналогично определяются начальные и конечные моменты времени остальных интервалов постоянства скорости электродвигателя. Очевидно, что конечный момент времени последнего интервала постоянства скорости должен совпадать с tK.

Величина At, а значит и количество отсчетов N дискретной функции выбираются из следующего условия: для любых трех значений дискретной функции Lj (tj - At), Lj (t{) и Lj (tj + At)

должно выполняться неравенство

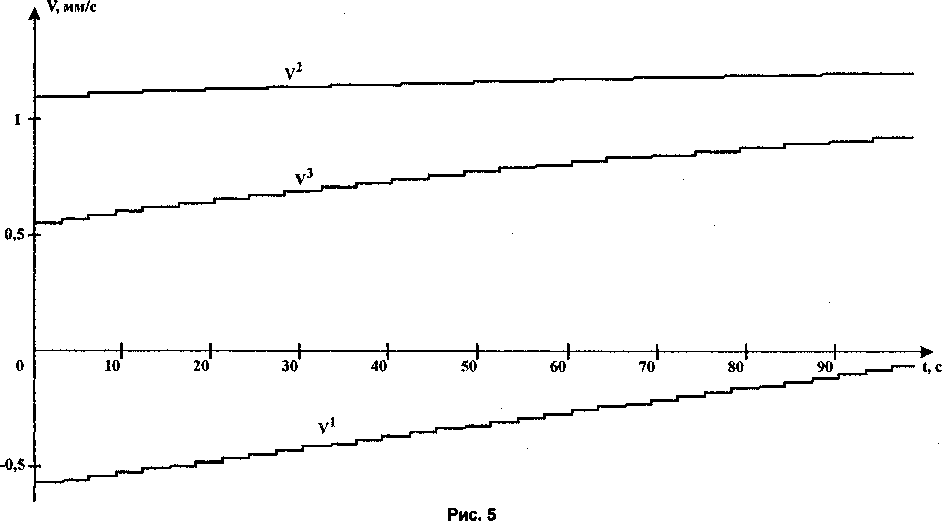
Представленная методика позволяет определить для каждого двигателя интервалы постоянства его угловой скорости. Количество этих интервалов будет различным для двигателей разных штанг. На рис. 5 показаны результаты моделирования поведения рассматриваемого механизма в случае, когда координаты его характерной точки К изменяются по линейному закону от (-50,40,200) до (50,80,270) за N = 100 временных отсчетов. При моделировании было принято, что координаты заданы в миллиметрах, временные отсчеты - в секундах, AL_max =0,01 мм.

Из графиков видно, что скорость электродвигателя 1-й штанги изменяется 33 раза, 2-й штанги -12 раз, 3-й штанги - 24 раза. Всего наблюдается 55 моментов изменения скоростей двигателей.

В связи с тем, что реальная длина штанг механизма в каждый момент времени в той или иной степени отличается от требуемой, целесообразно оценить точность формирования траектории движения характерной точки. На рис. 6 показаны абсолютные отклонения реальных координат характерной точки от требуемых: Др = -^Ах² + Ay² + Az.² , Ах = х_РЕАЛ-х^ , Ау = у реал ~ Утр > А^{2 = 2}реал ~ ^ztp • Под требуемыми координатами понимаются значения. x(t_n), y(t_n), z(t_n). Реальные координаты определяются при решении прямой задачи движения рассматриваемого механизма - задачи определения координат характерной точки механизма по заданным длинам его штанг. Длины штанг при решении этой задачи задаются исходя из ступенчатого управления скоростью электродвигателей (см. рис. 5).

Рис. 6

Анализ отклонений, показанных на рис. 6, позволяет сделать важный практический вывод: погрешность формирования траектории характерной точки механизма не превосходит величины заданного максимального отклонения АЬмдх, задаваемого при организации управления электродвигателями штанг. Таким образом, величина ALj^ может задаваться исходя из требуемой точности формирования траектории движения характерной точки.