Алгоритм восстановления поверхности объекта по его изображению

DOI:

,

Доктор физико-математических наук, заведующий кафедрой компьютерных наук и экспериментальной математики, Волгоградский государственный университет ,

В настоящей статье рассматривается задача построения каркаса поверхности, если известна его центральная проекция на некоторую плоскость. Эту задачу можно отнести к общей задаче фотограмметрии при анализе одиночного снимка. Нужно отметить, что задача восстановления поверхности возникает и при сканировании, объекта, когда карта глубин имеет дефекты и искажения [1], и когда поверхность строится по облаку точек [7], и когда сама поверхность обладает свойством зеркальности [6]. Вообще говоря, однозначно определить пространственные координаты точки по ее проекции нельзя, однако при имеющейся дополнительной информации это сделать удается. Например, если известна высота съемки и то, что искомые точки располагаются на горизонтальной плоскости [5]. Другой дополнительной информацией могут быть известные углы между некоторыми точками в пространстве. Простейшей здесь задачей является задача нахождения вершин пространственного треугольника по координатам проекций его вершин при известных углах треугольника. Данная задача рассматривалась в работе [4]. При исследовании задачи о вычислении параметров плоскости пространственного треугольника по его центральной проекции в этой работе были установлены условия существования и единственности решения. Помимо этого, был предложен алгоритм приближенного поиска всех возможных решений задачи при выполнении найденных условий. В настоящей статье мы применяем разработанный алгоритм для восстановления триангулированной поверхности по ее центральной проекции на некоторую плоскость, а также для определения пространственной ориентации здания по его фотоснимку. Дадим необходимые обозначения и более точную формулировку задачи.

Мы предполагаем, что центральная проекция имеет центр в начале координат, а проектирование происходит на плоскость г = d . Таким образом, центральная проекция имеет вид

(ж.у.г) ^ (Л'.К)= (^.^) , где (ж, у, г) — точка в пространстве, величины X, У есть координаты проекции этой точки в плоскости г = d.

Пусть в пространстве расположена поверхность S, заданная уравнением г = /(ж, у), где (ж, у) принадлежит некоторой плоской области Q. Мы предполагаем, что на поверхности S задана треугольная сетка в виде набора треугольников {Тк}к=1, вершинами которых являются точки из конечного набора {Рг}"=1, лежащие на поверхности S. Пусть (жг,уг,гг) — координаты точек Рг, где гг = /(жг,уг). Мы будем предполагать, что этот набор треугольников образует триангуляцию поверхности S, то есть каждая точка Рг принадлежит какому-то треугольнику Тк только в качестве его вершины, а треугольни ки могут пересекаться только по своим сторонам. Через ак, вк, Yk будем обозначать углы треугольника Тк. Пусть Qг,г = 1,..,т — центральные проекции точек Рг. Qг = (Хг ,У,Р) и

Тогда

жгd         угd

Х г = —, У =   .

г г

г г

Задача состоит в следующем. Зная координаты точек Q^ способ соединения их в треугольники и углы этих треугольников а _к , в _к , Y _k , требуется найти координаты точек (ж _г ,у _г ,г _г ) . Под способом соединения мы понимаем набор из троек натуральных чисел (г к , г к ,г к ) , к = 1 ,..., N , означающих номера точек Р _г , которые образуют треугольник Т _к .

Отметим, что даже для одного треугольника решений бесконечно много (треугольник определяется с точностью до гомотетии). Поэтому мы будем считать, что хотя бы одно из значений 2 _г нам известно. Для определенности предполагаем, что известно 2 0 . Очевидно, что поставленная задача сводится к восстановлению каждого треугольника T _k в отдельности.

Остановимся подробнее на описании алгоритма для отдельного треугольника и некоторых особенностей его реализации. Для начала отметим, что вопрос о восстановлении параметров искомой плоскости треугольника сводится к решению системы двух квадратичных уравнений вида

J F(и, v) = а 1 и ² + a ₂ uv + a ₃ v ² + а ₄ и + a ₅ v + а ₆ = 0 , | G(u, v) = Ь 1 и ² + b ₂ uv + b ₃ v ² + b ₄ u + b ₅ v + b ₆ = 0 ,

где коэффициенты уравнений известны и вычислены через углы исходного треугольника и углы его проекции [4]. Неизвестные переменные u,v имеют такой смысл. Если искомые вершины треугольника Р 1 , Р ₂ , Р ₃ , то

1^ 2 |

|Р з |

^U = Р , ^V = Р •

Алгоритм решения этой системы уравнений следующий:

• 1)    Определяется прямоугольник R = [ и 1 ,и ₂ ] х [ v 1 ,v ₂ ] в плоскости параметров ( и, v ) , в котором расположены корни данной системы уравнений. Если кривая второго порядка из системы (1) является эллипсом, то мы рассматриваем прямоугольник, описанный вокруг него. Если обе кривые являются эллипсами, то берем пересечение таких прямоугольников.

• 2)    Проводя прямые линии и = (и 1 + и ₂ ) / 2 и v = ( v 1 + v 2 ) / 2 , прямоугольник R разбивается на четыре равных прямоугольника R 1 ,R ₂ ,R ₃ ,R ₄ . Далее выбираются из этих прямоугольников только те, каждый из которых пересекает обе кривые второго порядка, соответствующие уравнениям системы (1). Проверка пересечения осуществляется так. Рассматривая каждое уравнение, мы проверяем, имеется ли точка пересечения соответствующей кривой со сторонами прямоугольника, что сводится к вопросу о количестве корней некоторого квадратного уравнения.

• 3)    Далее для каждого из выбранных прямоугольников мы повторяем шаг 2, рассматривая его в качестве прямоугольника R . Повторяем эту процедуру до тех пор, пока размеры получающихся прямоугольников не будут отвечать требуемой погрешности вычисления корней системы (см. рис. 1).

Отметим, что с помощью данного алгоритма мы найдем пары ( и, v ) , которые позволят вычислить все вершины треугольника. Получим формулы для этого. Зафиксируем треугольник, и пусть Р _г 1 , Р _г 2 , Р _г 3 — его вершины. Если известна величина |Р _г 1| , то получаем такие формулы:

Рц =

1 Р . 1 I

IQ « i I

Q » i ,

Р г 2

_{= п}^|Р* 1¹       р. ₌ у 1^11

^{и       q} » 2 , г з ^{v      Q} » 3

^IQ i 2 |                       ^|Q г з |

Для вычисления нормального вектора плоскости треугольника мы используем следую- щие формулы:

N =

l х п |C ^{х l|},

где

q*   q^

---.

Q I   Q I ’

η

03_

I Q i 3 I

Qu

^|Q i 1 |

Отметим, что точки можно вычислить и с помощью таких формул:

—                                    ~*

- ^lPi1 ¹ Q.    p. - Q. '-P, ^{Pi t}    p. - Q. ^iN, ^Pi1 ^

I Q. I ^Q1 1 ,  ^{Z Q t} 2 (MQ . 2) ’   " ^{Q i} 3 M ) •

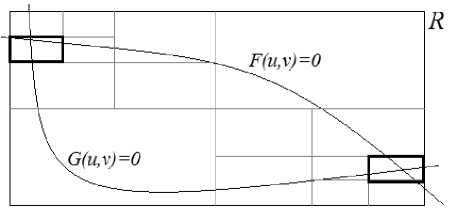
Рис. 1. Поиск решений системы уравнений (1)

Описание алгоритма восстановления поверхности

Как было отмечено выше, треугольник по своей центральной проекции восстанавливается с точностью до гомотетии. Однако, даже если зафиксировать одну его вершину, то и в этом случае однозначного решения может не получиться (см. работу [4]). Это связано с тем, что система (1) может иметь не единственное решение. В то же время с помощью описанного выше алгоритма можно найти все приближенные решения системы (1). По этим решениям легко определяются из формулы (2) нормали плоскостей, в которых может лежать искомый треугольник. Поэтому основной проблемой при восстановлении поверхности является выбор одной из вычисленных нормалей.

Итак, нам дан набор точек {Q _i } i=1 с координатами (Х _г ,У _г ) . Так же нам известно, что треугольник Т образован вершинами с номерами ( г к,гкр^ ) , то есть Т _к = = ^Р_г 1 РрРр • Нужно отметить, что такая конструкция носит название триангуляции и используется нами в разных задачах аппроксимации интегралов [3] и дифференциальных операторов [2]. Для восстановления поверхности мы фиксируем определенный порядок прохода по треугольникам сетки, чтобы нормаль соседнего треугольника уже была вычислена. Поэтому, мы считаем, что задан набор чисел П 1 , п ₂ , ..., п _к , которые имеют следующий смысл. Во-первых, полагаем П 1 = 1 . Во-вторых, п _т < г есть номер некоторого треугольника, который имеет общую сторону с треугольником Т _т . Как было сказано выше, для каждого треугольника Т _к с помощью системы (1) вычислены векторы нормали N k. ,..,N ^l _k ^k плоскостей, в которых может находиться искомый треугольник, и таких, что ( N ³ _k , е ₃ ) >  0 , е ₃ = (0 , 0 , 1) .

Дадим описание алгоритма. Он основан на том, что нормаль гладкой поверхности меняется непрерывно. Поэтому, мы выбираем ту нормаль из возможных вариантов, которая минимально отличается от нормали некоторой соседней ячейки.

• 1)    Обозначим через N 1 нормаль плоскости первого треугольника.

• 2)    Продолжаем с к = 2 . Выбираем треугольник Т и вычисляем все векторы N _k ,.., N ^l _k .

• 3)    Находим такой номер j _k , на котором достигается минимум величины l N — N_{Tl k} | , 3 = 1 , 2,..,1 _к .

• 4)    Полагаем N _k = N ^ .

• 5)    Пусть R одна из общих вершин треугольников Т _к и Т_Пк . Так как n _k < к , то вершины треугольника Т_Пк вычислены. В частности, известны координаты точки R . Другие две вершины треугольника Т _к вычисляем по формулам (3).

Тестовые примеры показали достаточно высокую точность вычисления координат нормального вектора для плоскости восстанавливаемого треугольника. Решение данной задачи было применено для реализации алгоритма восстановления поверхности по центральной проекции треугольной сетки с заданными углами, нанесенной на эту поверхность.

Пример 1. Рассмотрим поверхность, заданную уравнением z = —0.2x2 + 0.5y2 + + 3, где (x,y) G Q = [0,2] х [0,2]. Разобьем прямоугольник Q на pq прямоугольников прямыми x = xi,y = yj, где xi = 2г/р, г = 0, ...,р, yj = 2j/q, j = 0, ...,q.

Каждый такой прямоугольник разделим диагональю на два треугольника. В итоге получим ( p + 1)( q + 1) точек и 2pq треугольников. Мы считаем, что координаты проекций точек (x i ,y j ,Z ij ) , z _ij = / (x i ,y j ) известны. Взяв р = q =10 , мы получили набор точек Q ij ^{( x} i ^ ^/z ij ^,y j ^ ^/z ij ) •

В результате по заданной плоской сетке (см. рис. 2) была восстановлена пространственная треугольная сетка, причем погрешность вычислений составила 6.21e-05. Приведем изображение полученной поверхности с нескольких ракурсов (см. рис. 3).

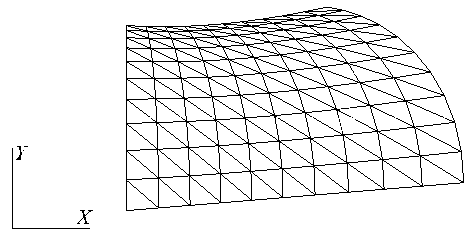
Рис. 2. Проекция треугольной сетки, нанесенной на эту поверхность

Определение ориентации здания по фотоснимку

Рассмотрим задачу определения угла поворота здания относительно плоскости фотокамеры. Для этого можно воспользоваться описанным выше алгоритмом. Будем считать, что здание имеет архитектурные элементы (треугольные или четырехугольные), в которых заранее известны углы. Например, мы можем считать известным отношение сторон оконных проемов здания, высоты и ширины самого здания, углов между скатами крыши и т. д.

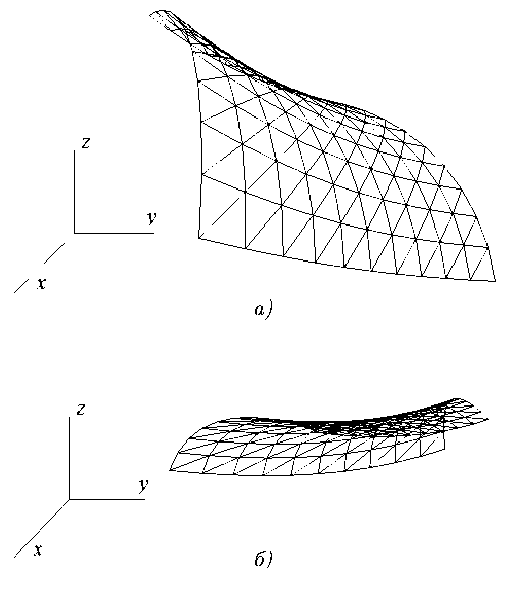
Рис. 3. Восстановленная поверхность

Для примера рассмотрим снимок 3D модели здания, выполненного в программе Blender с известным углом поворота вокруг вертикальной оси. Прежде чем решать систему уравнений (1), мы определили коэффициент для перевода координат в пикселах в те же единицы измерения, которые установлены в программе Blender. Это позволило воспользоваться значением фокусного расстояния (значение параметра d ) из той же программы. Чтобы минимизировать погрешность вычислений, мы рассмотрим достаточно удаленные друг от друга три точки на снимке, как показано на рисунке 4 а. Координаты этих точек на самом изображении в пикселах Q 0 = (97 , 36) , Q 1 = (98 , 88) и Q 2 = (146 , 85) . Решая соответствующую этому случаю систему (1), мы получили значение угла поворота, равное 0 , 499 . Настоящее значение угла равно 0 , 481 , что соответствует погрешности в 0 , 018 радиана, или приблизительно 1 , 03 ° .

Для проверки были рассмотрены и другие тройки точек. Например, выделим точки, как указано на рисунке 4б. Координаты этих точек Q 0 = (54 , 33) , Q 1 = (54 , 89) и Q 2 = (91 , 35) .

Решая соответствующую этому случаю систему (1), мы получили значение угла поворота, равное 0 , 468 , что соответствует погрешности в 0 , 013 радиана, или приблизительно 0 , 71 ° . Остальные измерения и вычисления дали погрешность в среднем 0 , 84 ° . В следующей таблице приводятся результаты вычисления угла поворота по ряду измерений опорных точек Q 0 , Q 1 и Q 2 по снимкам здания с разных позиций.

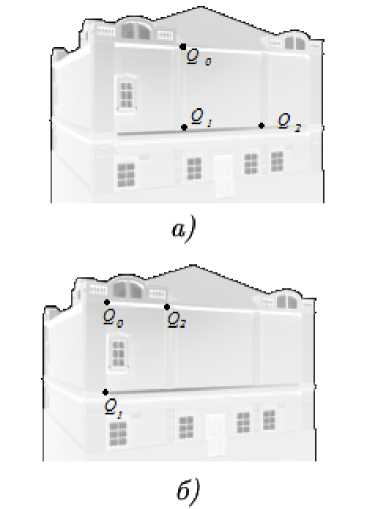
Рис. 4. Снимок здания с отмеченными точками

Учитывая, что изображения имели разрешение всего лишь 240 х 135 пикселей, неизбежными были ошибки при измерениях координат точек Q 0 , Q 1 и Q 2 . Поэтому, полученную погрешность в вычислении углов поворота здания можно считать вполне удовлетворительной.

Точное значение угла поворота	Вычисленное значение угла поворота	Погрешность
27 , 55 °	28 , 590 °	1 , 03 °
13 , 80 °	14 , 43 °	0 , 63 °
27 , 55 °	26 , 81 °	0 , 74 °
13 , 80 °	13 , 12 °	0 , 68 °
17 , 01 °	18 , 22 °	1 , 20 °

Заключение

В данной работе была рассмотрена задача восстановления пространственных объектов или их частей по изображению центральной проекции этих объектов. Статья содержит алгоритм решения поставленной задачи и описание двух примеров такого восстановления. В первом примере показано вычисление координат вершин треугольной сетки, нанесенной на некоторую поверхность. Второй пример показывает возможность вычисления угла поворота здания относительно фотокамеры с помощью анализа плоского изображения здания.