Алгоритм вычисления признаков отрезков на растровых изображениях

Существует большой класс изображений, которые созданы непосредственно человеком, например, рукописи, чертежи, схемы, карты. Главной особенностью таких изображений является то, что основные объекты, составляющие главную сцену, можно представить набором отрезков [1-2].

Поиску отрезков на изображениях посвящено множество работ, в большинстве которых используются классические методы, основанные на выделении, утончении границ, сегментации, прослеживании контура и устранении разрывов [3-4]. Достоинствамитаких методовявляютсядовольно высокое быстродействие и простота реализации. Однако перечисленные методы подходят только для поиска отрезков на малонасыщенных изображениях из-за следующих недостатков:

• -    результат является приближенным;

• -    результат может содержать лишние примитивы (кривые линии);

• -    отсутствие численных признаков отрезков;

• -    наличие постороннего шума в виде бахромы.

Применение метода линейной аппроксимации позволяет избавиться от перечисленных недостатков [5], но позволяет выделить только одну линию на изображении.

Для более точного решения такой проблемы используют интегральные преобразования (ИП) по линиям [6-7]. В результате ИП формируется спектральная функция, максимумы которой будут соответствовать параметрам линии.

ИП позволяют найти прямые на изображениях независимо от длины, расположения и ориентации на довольно сложных изображениях. ИП по линиям могут быть модифицированы для поиска отрезков. Например, отрезок может быть представлен координатами концевых точек, то есть

Ткачук М.И.

требуется четыре параметра. Для четырех параметров ИП становится довольно трудоемким и практически становится нереализуемым.

В работе [2] применяется следующая модификация ИП по прямой линии. Результатом преобразования является спектральная функция, хранящая список линейных сегментов, лежащих на данной прямой. В этот список входят координаты концов отрезка, значение направления модуля градиента для данного отрезка и количество точек. Описанный способ может быть изменен таким образом, чтобы искать отрезки не в момент ИП, а после того, как все линии будут найдены. Такой подход позволит, исследуя линии, определить не только сегменты, но и подавить шум и устранить разрывы. Из анализа существующих методов следует, что задача не является полностью решенной, поэтому актуальной является разработка новых более качественных и быстродействующих алгоритмов вычисления признаков отрезков как границ полигональных объектов на растровых изображениях.

Предположим, что отрезки можно выделить как части линий. Целью данной работы является разработка и исследование алгоритма выделения признаков линейных сегментов на растровом изображении с помощью ИП по прямой линии с последующим поиском отрезков на этой прямой.

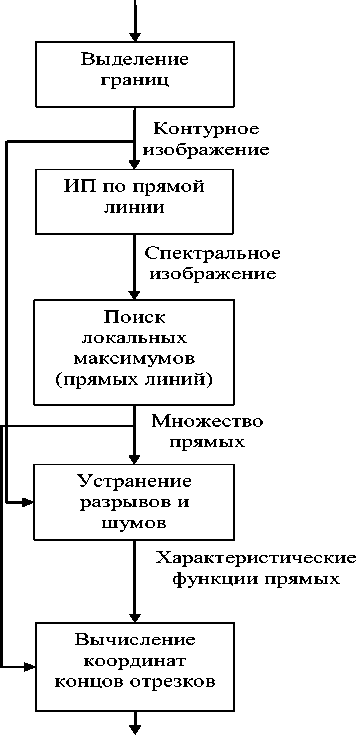
Общая схема алгоритма

Общая схема выделения отрезков представлена на рис. 1. Далее каждый шаг алгоритма рассмотрен более подробно.

Выделение границ . В большинстве случаев отрезки являются частями границ полигональных объектов. При этом за счет выделения контуров объектов изображения поиск линейных сегментов значительно сократится. Одним из способов выделения границ являются методы пространственного дифференцирования, которые основаны на предположении о том, что граничные точки имеют большую величину модуля градиента функции яркости [8].

Градиент яркости – это вектор, ориентированный по направлению наиболее быстрого возрастания яркости и имеющий длину, пропорциональную этой максимальной скорости изменения яркости (максимальному значению частной про- изводной по направлению) [8]. Функцию градиента будем использовать для увеличения быстродействия интегральных преобразований.

Исходное изображение

Множество отрезков

Рис. 1. Схема вычисления признаков

Модуль вектора градиента определяет границы, то есть насколько в данной точке границы отличаются яркости объекта и его окружения. Угол наклона вектора градиента показывает направление наибольшего изменения яркости, то есть этот вектор направлен перпендикулярно границе.

В двумерном случае вектор градиента яркости определяется как:

r

G ( x , У ) =

d fCx iZl r ₊ d x

^{d f (} x , У ) r d y

где i и j – единичные векторы, направленные вдоль осей Ox и Oy , соответственно.

Модуль градиента определяется как:

( ^d f ^{( x} , У ) ) ,ff^{f ( x} , У ) )

x, У) — II +

⎝    ∂x    ⎠    ⎝∂ а направление:

d f ( x , y ) d f ( x , y ).

Ф ( x , y ) = Arctg (^^-^/ ^^-^) ■

∂y∂

Ширина контура изображения может быть различной, поэтому для выделения контуров применяется адаптивный метод [10]. Используются два фильтра:

s x ( x , y ) =

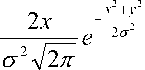
x ² + y ² 2g²

s y ( x , y ) =

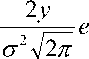
где параметр определяет ширину контура. Значение координат градиента определяется по сверткам:

∞∞

Gx = J Jf (x " x0 , У " У0 )sx (x, y)dxdy ’ -∞-∞ ∞∞

Gy = J J"f (x " x0, y " y0)s y(x, y)dxdy ■ -∞-∞

После выделения контуров производится бинаризация изображения. Процесс бинаризации заключается в следующем: определяется пороговая величина,после чего значение в каждой точке контурного изображения сравнивается с этим порогом, и если значение функции меньше, то функции бинарного изображения в данной точке присваивается значение ноль, в противном случае – единица.

Если аппроксимировать гистограмму модуля градиента равномерным распределением вероятности, то порог будет вычисляться как удвоенное среднее модуля градиента.

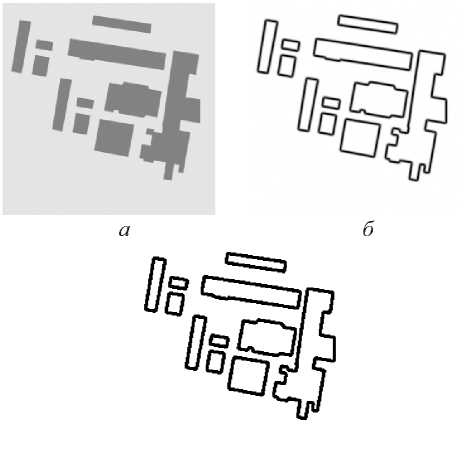
На рис. 2 представлен фрагмент карты ( а – исходное изображение, б – контурное, в – бинарное изображение).

Градиентное интегральное преобразо вание по прямой линии. Для ИП по прямой необходимо знание двух параметров нормали к прямой линии: длину и угол наклона к оси Ox ■ Длина может быть вычислена, а угол может быть получен прямым перебором возможных значений. Однако так как известна функция направления модуля градиента яркости изображения, то вместо обычного ИП можно использовать градиентное ИП (ГИП), что позволит увеличить быстродействие за счет исключения поиска угла наклона прямой, так как вектор градиента ортогонален ей.

в

Рис. 2. Изображения карты

Пусть R ² - областьизображения; b : R ² ^ {0,1} – функция бинарного изображения, получаемая бинаризацией модуля вектора градиента яркости изображения; ( x , y ) - точка на плоскости R ² (( x , y ) e R ² ) , Ф : R ² >  [0,2 п ) - функция угла наклона вектора градиента яркости на изображении.

Прямая задается с помощью нормального уравнения:

x cos 0 + y sin 0 - p = 0, где 6 и p - угол наклона и длина нормали прямой (см. рис. 3).

Алгоритм ГИП выглядит следующим образом:

V ( x, y) | b( x, y) = 1

h(p, 0 ) = h ( p , 0 ) + dxdy

О = Ф ( x, y )

p = x cos0 + y sin 0 .

Данное преобразование позволяет определить для прямых линий на растровом изображении параметры нормали, проведенной к линии. Каждое отличное от нуля значение параметрической функции h ( p , 0 ) определяет количество точек, лежащих на линии, нормаль которой определяется аргументами р , 0.

Поиск локальных максимумов спектраль ной функции. В идеальном случае на изображении должны определиться все линии, однако из-за ошибки дискретизации либо наличия полос вместо одной линии могут появиться линии-помехи, имеющие малую длину. Чтобы избежать появления таких нежелательных линий, в работе используется алгоритм анализа значений параметрической функции.

Определяется максимум h _max параметрической функции h ( p , 6 ) :

h max = ^max h (p, 9) •

∀ρ,θ

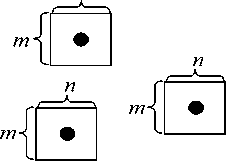
Далее задается минимальное количество точек h _{mi n} , лежащих на линии. Просматривается каждый максимум l ( l е [h max , h _{mi n} ] ), если максимум существует, то вокруг него формируется область d размером m x n , в которой обнуляются все значения спектральной функции (см. рис. 4).

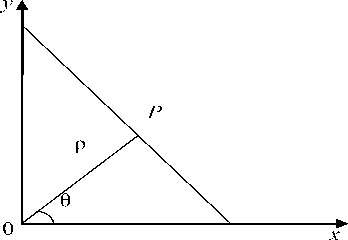
Рис. 3. Параметры прямой

ГИП для прямых линий записывается в следующем виде [7]:

h(p, 0 ) = jj b(x, y ) 5 [ x cos Ф (x, у) + у sin Ф (х, у) -

R ²

— РИ Ф (х, у ) — 0 ] dxdy.

Рис. 4. Удаление линий-помех

Алгоритм поиска локальных максимумов будет состоять из следующих шагов.

• 1.    Задание минимального значения спектральной функции (минимальная длина линии) h mi n .

• 2.    Поиск максимального значения спектральной функции h . max

• 3.    Поиск локальных максимумов l на промежутке [ h max , h min ] и построение вокруг них области d размером m х n .

• 4.    Обнуление значений спектральной функции в окрестности d локального максимума.

• 5.    Шаги 3 и 4 выполняются, если максимум l больше заданного порога h min .

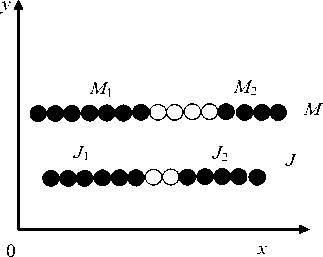
длину разрыва и минимальный размер отрезка. Если отрезок имеет длину L , то L сравнивается с X. Если L < X , отрезок считается ложным.

На рис. 6 длина отрезка L i меньше X, поэтому данный отрезок не удаляется (точки отмечены серым), длина отрезка L ₂ больше λ, поэтому данный отрезок остается (точки отмечены черным).

Формирование сечения. По каждой найденной прямой сформируем сечение V изображения, которое представляет собой характеристическую функцию присутствия отрезка на прямой: V ( t ) = 1 - если точка контура находится на пря-

мой, V(t) = 0 - иначе.

Пусть 0 i , p i - угол наклона и длина норма-

ли i -прямой, Rot =

θ

⎛cosθ -sinθ⎞ ⎜⎟ ⎜⎝ sin θ cos θ ⎟⎠

– оператор

y

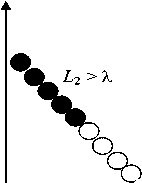
L i < X

вращения прямой на угол 0 , At = -^

22 x max + y max

– максимальная длина прямой в пределах изображения, тогда для формирования сечения будем

Рис. 6. Устранение шумов

x

использовать следующий алгоритм:

1. Для каждого значения t из интервала

[ - A t , A t ] определим координаты точек

/

x

⎝ ^y ⎠

= Rot ⎜

θ

⎛ρ i ⎞

⎝ ^t ⎠

2. Если B( х, у ) = 1, то V ( t ) = 1 , иначе V(t) = 0 .

На рис. 5 показано сечение линии L , черными отмечены точки, в которых функция контурного изображения равна 1 ( В ( х , у) = 1), белыми - 0 (B(х, у) = 0).

Пусть существуют два отрезка L i и L 2 , лежащие на одной прямой, r – расстояние между ними. Если r то будем считать, что r - длина разрыва, и отрезки L i и L 2 объединяются в отрезок L , иначе на прямой существуют два отрезка.

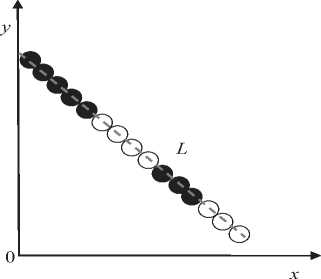
Рис. 5. Формирование сечения

y

а

M 1           M 2

M

J 3

J

Устранение разрывов и шумов. Сформированное сечение может состоять из множества отрезков, причем некоторые отрезки могут быть ложными (шум), а другие – разорванными. Для корректного выделения отрезков необходимо устранить разрывы и шумы, которые могут присутствовать после выделения прямых линий. Зададим величину X, характеризующую максимальную

--------------------------► 0                         x

б

Рис. 7. Пример разрыва

На рис. 7: X = 3, на прямой линии Mлежат два отрезка M 1 и M2, расстояние между которыми г = 4 (г > X), на прямой линии J лежат два отрезка J1 и J2 , расстояние между которыми Г = 2 (Г2 < X), поэтому эти отрезки объединяются в отрезок J3 . На рис. 7а - исходное изображение, 7б – удаление разрыва.

Устранение разрывов и сегментов малой длины реализуется формулой:

λ/2

V = у JV (t + 10) d 0 . λ -λ/2

После устраненияразрывов и шумов определяются координаты начала ( X i , у ) и конца ( Х 2 , у 2 ) всех отрезков, лежащих в данном сечении.

Исследование разработанного алгоритма

Проведем исследования разработанного алгоритма на тестовых и реальных изображениях.

Тестовые изображения будем генерировать по схеме, представленной на рис. 8.

Размер изображения,    Уровень количество вершин, шума

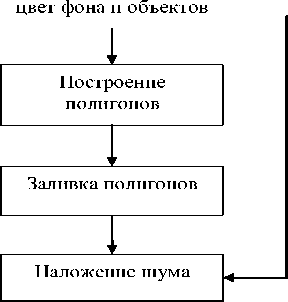
Рис. 8. Формирование тестового изображения

Отрезками являются стороны полигональных объектов. Наложение многоугольников друг на друга позволит сгенерировать отрезки, лежащие на одной прямой линии.

На полученное тестовое изображение будем накладывать аддитивный гауссовский шум g (о) . Величина шума определяется параметром среднего квадратического отклонения (СКО) о .

В представленной модели генерации тестовых изображений присутствуют как точные характеристики: яркость фона и объектов, размер, максимальное число вершин полигонов, так и случайные признаки: действительное количество полигонов, вершин, расположение вершин, перекрытие многоугольников объектами цвета фона. Для исследования будем применять метод статистического имитационного моделирования [3]. Сформируем две функции F ( х , у) и G ( х , у) .

Значения функции G ( х , у) равны единице, если точка принадлежит выделенному отрезку. Значения функции F ( х , у) равны 1, если точка принадлежит контурному изображению оригинала без шума, и 0 в противном случае.

а                      б

в

Рис. 9. Тестовые изображения

Будем сравнивать изображения с помощью свертки. Сгенерируем 10 тестовых изображений и определим среднее значение количества точек совпадения для каждого уровня шума. Максимальное количество многоугольников и вершин зададим 8, яркость объектов от 20 до 100, размеры 256 на 256 пикселей. Данные приведены в таблице 1.

На рис. 9 представлено несколько тестовых изображений. На рис. 10 построен график зависимости количества точек совпадений k от СКО σ .

Таблица 1. Зависимость коэффициента k от СКО

№/a	0	20	40	60	80	100
1	667	647	660	654	635	597
2	717	667	716	678	685	711
3	423	416	367	383	397	382
4	500	500	499	493	484	471
5	505	483	444	445	434	474
6	510	474	464	457	466	464
7	645	673	604	613	597	596
8	566	566	561	566	540	564
9	704	696	691	646	617	687
10	570	581	586	592	580	495
Среднее	580	570	559	552	543	544
Нормированное	1	0,98	0,96	0,95	0,93	0,93

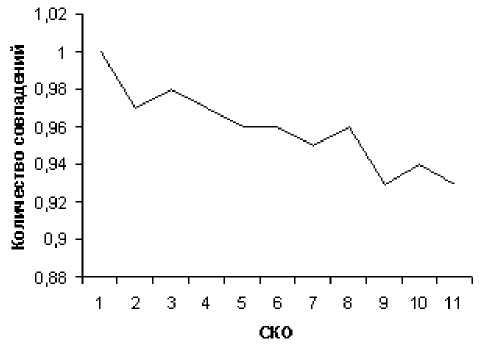
Рис. 10. График зависимости оценки k от СКО σ

Также приведем результаты для изображения карты на рис. 1 1 ( а – исходное изображение, б – результат выделения отрезков).

А                    б

Рис. 11. Результат выделения признаков отрезков

Заключение

Результатом данной работы является алгоритм выделения отрезков на растровом изображении. Меняя значения параметров, такие как область вокруг локального максимума в спектральном пространстве, минимальную длину отрезка (максимальную длину разрыва), можно добиться наиболее приемлемого результата для конкретного изображения. Как показали результаты исследования (см. график на рис. 11 и таблицу 1 ), разработанный алгоритм устойчив к шуму. При увеличении уровня шума до 1000 отклонение от исходного значения составляет 8-10%. Так как многие объекты на изображениях могут быть представлены отрез-ками,поэтому данный алгоритм может быть использован для выделения полигональных объектов, преимущественно на технических изображениях.