Алгоритма для распределенных систем с шардированием для инфраструктуры устройств межмашинного взаимодействия

Объем информации в мире стремительно растет, что обусловлено увеличением количества пользователей, появлением новых источников данных. Одним из важных факторов роста является развитие интернета вещей, который включает в себя устройства межмашинного взаимодействия. Эти устройства генерируют огромные объемы данных, что приводит к необходимости масштабирования инфраструктуры для их обработки и хранения.

По некоторым оценкам, объем информации в мире удваивается каждые четыре года. Это лавинообразное нарастание информации связано с тем, что устройств межмашинного взаимодействия уже больше, чем людей, и это приводит к значительному увеличению автоматически генерируемых данных.

Источники больших данных

Классическими источниками больших данных являются: интернет вещей, социальные медиа, данные, генерируемые внутренними системами предприятий, и другие источники. Устройства интернета вещей, такие как сенсоры и другие измерительные устройства, непрерывно отправляют данные, что существенно увеличивает общий объем информации.

Этот рост требует значительных инвестиций в инфраструктуру, включая платформы хранения данных, системы обработки больших данных и соответствующие аналитические инструменты. Организации должны адаптировать свои информационные системы, чтобы справиться с возрастающим объемом и разнообразием данных, обеспечивая при этом производительность, безопасность и масштабируемость1. Системы нуждаются в вы- сокой отказоустойчивости и согласованности данных, для чего применяются алгоритмы консенсуса на основе конечных автоматов2.

Алгоритм консенсуса

Распределенные сети и шардирование помогают в масштабировании, но имеют недостатки. Первые требуют согласования операций, увеличивая нагрузку на сеть, а шардиро-вание повышает уязвимость к потере данных. Комбинирование этих подходов позволяет достичь баланса между отказоустойчивостью, пропускной способностью и емкостью сети. В распределенных сетях теряется согласованность данных, и отдельный узел не может принять решение по некоторой операции единолично. Для решения этой проблемы используются алгоритмы консенсуса, которые обеспечивают согласованность данных между узлами. Участники сети обмениваются сообщениями для распространения транзакций по всем серверам и принятия единого решения по конечному состоянию системы на каждом этапе.

Наиболее распространенным методом достижения консенсуса является репликация конечного автомата, при которой все узлы начинают работу из единого начального состояния и обмениваются данными для перехода к последующему состоянию [1].

Консенсусный алгоритм должен обладать следующими свойствами: сходимость, согласованность, целостность, отказоустойчивость. Алгоритмы консенсуса составляются на основе предположений о допустимых видах отказов узлов и наборе ограничений относительно доставки сообщений ввиду ненадежности компонентов и невозможности достоверно определить состояние других узлов.

Виды отказов узлов:

• -    аварийная отказоустойчивость – алгоритм допускает потерю связи с узлом, но не допускает дезинформацию или манипуляцию системой. Допустимо не более ( n – 1)/2 сбоев узлов за один раунд консенсуса [2].

• -    византийская отказоустойчивость – алгоритм допускает произвольное поведение части узлов, включая дезинформацию и манипуляцию системой. Допустимо не более ( n – 1)/3 сбоев узлов за один раунд консенсуса [3].

Распределенные системы разделяются по модели коммуникаций на три класса:

• 1)    синхронная модель – предполагается, что существует известная верхняя граница времени задержки доставки сообщений Δ;

• 2)    асинхронная модель – сообщения могут быть доставлены за бесконечное количество времени. Доказано, что при этой модели коммуникации невозможно различить узел, вышедший из строя, от сообщения, которое доставляется бесконечно долго;

• 3)    частично синхронная модель – протокол разделяется на две фазы операции – асинхронную и синхронную. При нормальной работе сообщения могут быть доставлены за неизвестное количество времени, но в итоге достигнут всех узлов не более чем за Δ времени. В случае происшествия алгоритм переходит в асинхронную фазу глобальной стабилизации (GST). Такая модель наиболее практична и описывает работу реальных систем [4–10].

Существует методы достижения консенсуса в распределенных системах, основанные на разных элементах: на лидере, экономике сети, затратной работе, голосовании, истории обмена сообщениями [11–18].

Разработка частично синхронного консенсусного алгоритма для распределенных систем ...

В большинстве распределенных сетей с шардированием используются алгоритмы Paxos, Raft и их модификации. Но они также имеют недостатки: возможность воздействия на состояние системы, высокая нагрузка на лидера и возможность лидера влиять на конечное состояние системы.

Гипотеза: алгоритм должен соответствовать следующим требованиям: сходимость, целостность, согласованность, аварийная отказоустойчивость, возможность трансграничных запросов к шардам, отсутствие периодов недоступности сети, возможность узлов восстановиться самостоятельно, порядок транзакций не должен контролироваться узлами, высокая нагрузка, гибкость. Требования особенно важны в контексте применения алгоритма – в концепции межмашинного взаимодействия, позволяющей устройствам обмениваться данными и взаимодействовать друг с другом без непосредственного участия человека, и где в виде участников сети выступают маломощные устройства.

Предполагается частично синхронная среда доставки сообщений, где сообщения при нормальной работе сети доставляются не более чем за Δ времени, которое заранее неизвестно узлам. Допускаются произвольные отказы сети вплоть до полной недоступности среды доставки. Восстановление сети после сбоев обозначается как GST, после этого события сеть становится вновь синхронной и доставляет все сообщения в пределах Δ.

Участники обмениваются друг с другом сообщениями через прямые соединения. При получении данных от соседа узел проверяет, встречал ли ранее эти операции, и либо обрабатывает и пересылает остальным, либо игнорирует.

В сети имеются две роли: рабочий узел и узел-клиент. Клиенты делают запросы сервису и по результату выполнения операции получают ответ. Узел может быть как клиентом, так и представителем сервиса одновременно, но требуется соблюдение порядка запросов от клиента к сервису.

Узлы внутри сервиса принадлежат к шардам, и метод определения принадлежности участника к шарду остается за реализацией конкретного приложения. Однако алгоритм предполагает обмен сообщениями между шардами.

Для уникальной идентификации каждого узла в рамках одного шарда используется примитив псевдоуникальных «универсальных уникальных идентификаторов» (UUID), определенный по стандарту RFC 4122. Этот примитив обеспечивает достаточно высокую устойчивость к коллизиям при генерации идентификаторов.

Для описания результирующего состояния раунда консенсуса используется некриптографическая хеш-функция. Инициализация начального состояния описана в последующем разделе первичного запуска сети. Каждое последующее состояние вычисляется с помощью записи типов операций за текущий раунд в экземпляр объекта хеш-функции в порядке их исполнения. Это означает, что алгоритм использует: UUID для уникальной идентификации узлов; хеш-функцию для описания состояния раунда консенсуса; обмен сообщениями между шардами для координации узлов. Формально получение начального состояния для следующего раунда описывается формулой:

seed [ i + 1 ] = H ( seed [ i ] , operations [ i ] ) , (1) где i + 1 - следующая итерация значения seed (первоначального состояния); H - хеш-функция, которая принимает два аргумента: текущее значение seed [ i ] и набор операций operations [ i ] .

Для достижения полностью упорядоченной трансляции сообщений и одинакового представления порядка операций в рамках одного раунда и шарда используется вариация примитива последовательной трансляции [19].

В пределах одного раунда у каждого узла есть свой слот для запроса об исполнении операции. Все слоты упорядочены в пределах одного раунда с помощью функции псевдослучайных перестановок. В качестве инициализации состояния генератора псевдослучайных чисел используется результирующие состояние предыдущего раунда. Это означает, что все узлы знают заранее, в каком порядке будут идти операции в рамках одного раунда; разрешение конфликтных операций не зависит от решения какого-либо узла; допускается повторение порядка в рамках одного раунда, что позволяет узлам отправлять пачки операций и принимать их независимо от того, будет узел работоспособен после отправки или нет.

Этот подход обеспечивает упорядоченную трансляцию сообщений и одинаковое представление порядка операций в рамках одного раунда и шарда, что является важным элементом алгоритма консенсуса.

Пример работы примитива показан на Рисунке 1. Формальное определение порядка операций с помощью примитива описывается формулой процесса перемешивания:

order [ i ] = shuffle ( seed [ i ] , active _ nodes [ i ] ) , (2), где shuffle - функция перемешивает элементы, используя текущее значение seed [ i ] и active _ nodes [ i ] - активные узлы, участвующие в алгоритме консенсуса, которые будут перемешаны как источник случайности. Это может быть полезно для распределения нагрузки или случайного выбора узлов для выполнения определенных операций.

Для соблюдения порядка запросов от клиентов в рамках одного узла предполагается, что узел использует FIFO-буфер с взаимоисключающей блокировкой. Это гарантирует, что узел сохраняет локальную согласованность.

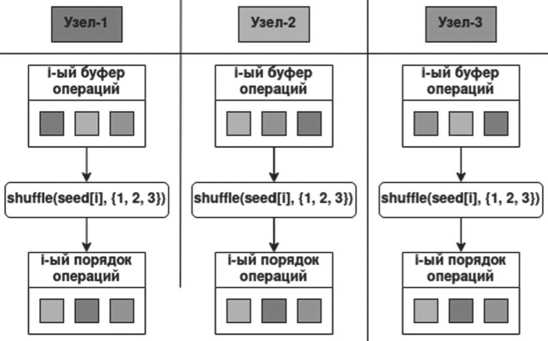
Рисунок 1. Результат работы примитива в i -м раунде Источник: здесь и далее рисунки выполнены авторами.

Для сокращения времени достижения консенсуса в текущем раунде в систему вносится операция NOOP, которая служит оповещением остальных узлов о дееспособности

Разработка частично синхронного консенсусного алгоритма для распределенных систем ...

узла в текущем раунде, и означает, что на момент начала нового цикла консенсуса у узла нет операций над системой. Вместо ожидания новых операций от других узлов и ответа им узел оглашает свою позицию на текущий раунд.

Это уменьшает время достижения консенсуса, поскольку узлы ожидают новых операций от других узлов, повышается эффективность системы, так как узлы могут быстрее оглашать свою позицию на текущий раунд и улучшается производительность системы, так как время достижения консенсуса сокращается.

Описание алгоритма

Шаг 1. Определить порядок выполнения операций order[i] с помощью функции shuffle(seed[i], active_nodes[i]) .

Шаг 2. Отправить пачку операций из локальной очереди соседним узлам сообщением , где node_id – идентификатор узла, который может быть уникальным для каждого узла в распределенной системе; epoch – раунд, в котором узел выполняет операции; ops – операции, выполненные узлом в данном раунде.

При нехватке операций в очереди на отправку узел дополняет пачку операцией пропуска действий NOOP .

Шаг 3. При получении операций от более чем половины узлов раунда, включая себя, считать, что произошла стабилизация сети GST и выставить таймер на Δ.

Шаг 4. По истечении таймера или получении n транзакций узел упорядочивает операции согласно order[i]. На место «пустых ячеек» вносит операцию отключения от сети, так как узлы потенциально потеряли связь с сетью или вышли из строя. Вычислить итоговое состояние раунда seed[i+1] с помощью хеш-функции H(seed[i], ops[i]) . Полученное состояние необходимо отправить соседям.

Шаг 5. При получении не менее n итоговых состояний, идентичных полученному узлом. Выполнить все операции раунда по порядку. Если же будет получено n + 1 seed’[i+1] состояний, отличных от полученного seed[i+1], то запросить недостающие операции, ко- торые помечены как «отключение от сети».

В одном раунде пачка операций применяется в том же порядке, что и одна операция, это позволяет экономить на задержках сети и сокращает время на согласование операций обратно пропорционально количеству допустимых операций в пачке. Сравнение порядка выполнения операций в раунде из одной транзакции на узел и пачки из четырех транзакций на узел показано на Рисунке 2.

На Рисунке 3 показан процесс достижения консенсуса в рамках одного раунда при отсутствии сбоев в сети четырьмя узлами: клиентом и тремя представителями одного шарда.

Клиент отправляет операцию узлу У1, которая попадает в очередь. В начале раунда У1 берет транзакцию из очереди, записывает в буфер и отправляет соседнему узлу. Узлы У1 и У2 получают транзакции друг друга и считают, что настал момент стабилизации GST. Узлы У2 и У3 обмениваются сообщениями, по итогу чего У2 получил все транзакции и вычислил итоговое состояние раунда. У1 получает последнюю транзакцию и вместе с ней итоговое состояние от узла У2. Узлы У2 и У3 получают состояния для сверки от узлов У1 и У2 соответственно. Узлы У2 и У3 передают крайним состояния противоположного участника для завершения протокола. После t6 все узлы сети успешно перешли на новый цикл консенсуса.

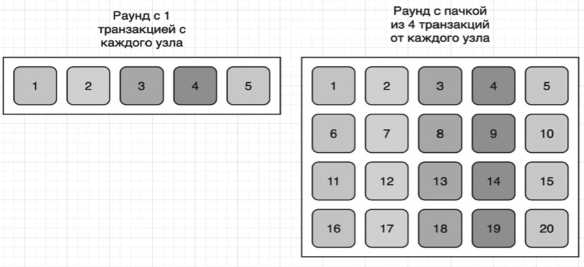
Рисунок 2. Разница в количестве транзакций при применении пачек в раунде консенсуса

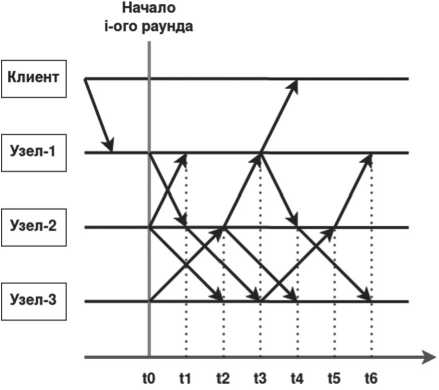
Рисунок 3. Процесс достижения консенсуса

Доказательство корректности: протокол гарантирует, что все узлы пришли к единому соглашению по предшествующему циклу и что действующий порядок будет у всех одинаков ( согласованность ); если операция определена системой, она будет принята всеми узлами ( целостность ); узлы смогут принять решение, даже если некоторые из них имеют отличные от имеющихся исходные состояния ( сходимость ); узлы смогут продолжить работу, даже если некоторые из них вышли из строя ( отказоустойчивость ).

При первом запуске сети участники генерируют свои идентификаторы и отправляют их всем, с кем есть соединение. При дубликатах узлы заново повторяют операцию генерации и отправки до тех пор, пока все участники не будут иметь индивидуальные номера. Процесс ограничивается таймером, по истечении которого сильно связные компоненты образуют новую сеть.

Состояние «ожидать GST» предполагает периодически отправлять свои операции соседним узлам для стабилизации сети и получения узлами сообщения. Это позволяет узлам распространять свои операции по сети и ожидать ответа от других узлов.

Для трансграничных транзакций между шардами необходимо иметь одинаковую некриптографическую хеш-функцию для определения шарда, ответственного за ключ. Это позволяет определить, какой шард должен обработать запрос.

Разработка частично синхронного консенсусного алгоритма для распределенных систем ...

Когда к узлу сделан запрос, а он не является частью ответственного шарда, следует присвоить уникальный идентификатор операции и отправить ее в сеть, где ответственный шард получит запрос и выполнит его через некоторое количество раундов консенсуса. Тогда трансграничные транзакции между шардами могут быть обработаны корректно, а клиент может получить ответ на свой запрос, даже если узел, к которому он обратился, вышел из строя.

Порядок выполнения трансграничной операции показан на Рисунке 4, где узлы, принадлежащие одному шарду, обозначены одинаковым цветом.

Таким образом, протокол обеспечивает возможность трансграничных транзакций между шардами и позволяет клиентам получать ответы на свои запросы даже в случае отказа узлов.

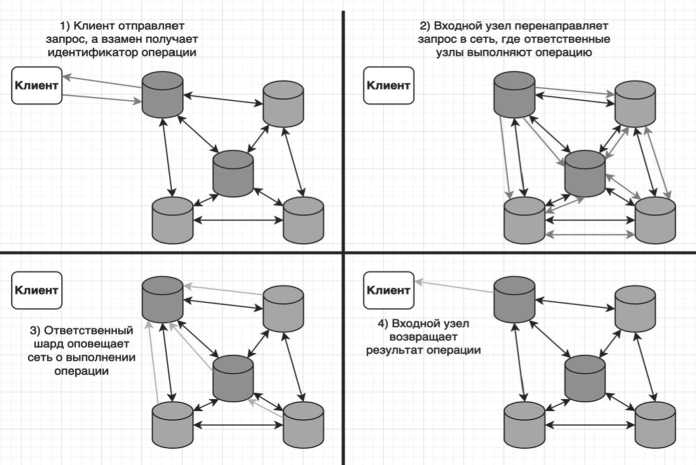
Рисунок 4. Выполнение транзакции между шардами

В этой модели клиент отправляет запрос на выполнение операции и указывает адрес, по которому необходимо доставить результат. Узел, ответственный за выполнение операции, получает запрос, выполняет операцию, затем отправляет результат операции прямо клиенту по указанному адресу.

Модель имеет следующие преимущества, которые особенно актуальны для концепции устройств межмашинного взаимодействия: сокращение количества шагов в последовательности, что делает систему достаточно быстрой; увеличение устойчивости к сбоям узлов, поскольку ответственный за запрос узел может выйти из строя, но результат операции все равно будет доставлен клиенту.

Существуют и ограничения: клиент должен указать адрес, по которому необходимо доставить результат; система должна быть способна доставить результат операции прямо клиенту, что может быть сложно в некоторых случаях.

Эта модель является альтернативой традиционной модели, в которой клиент дожидается исполнения операции и затем получает результат. Она может быть полезна для устройств межмашинного взаимодействия, когда клиент не требует немедленного ответа на свой запрос.

Для примера используем распределенную систему хранилища пар «ключ – значение», она будет состоять из множества реплик, каждая из которых будет иметь: очередь входящих операций, фильтр для повторяющихся операций; очередь входящих запросов на присоединение и событий отключения от сети, фильтр для повторяющихся операций; очередь запросов от клиентов; локальную копию хранилища «ключ – значение»; локальное хранилище технических данных; каналы связи с соседними узлами; обработчик событий.

Все входящие запросы будут добавляться в конец соответствующей FIFO очереди с взаимоисключающей блокировкой, что позволит повысить производительность за счет разграничения независимых операций и отсутствия долгих блокировок данных.

Для уменьшения нагрузки на примитивы синхронизации очередей все входящие запросы фильтруются с помощью соответствующих атомарных кэшей, которые без дорогих блокировок мьютексов смогут определить, встречалась ли ранее поступившая операция.

В реплике сервиса будет один поток обработчика данных, что позволит исключить блокировку на отправку исходящих запросов и ретрансляцию. Каналы связи должны работать асинхронно, вне зависимости от синхронности сетевого протокола.

Архитектура позволит обеспечить высокую производительность и устойчивость распределенной системы хранилища пар «ключ – значение». На Рисунке 5 показана схема взаимодействия компонентов одной реплики сервиса.

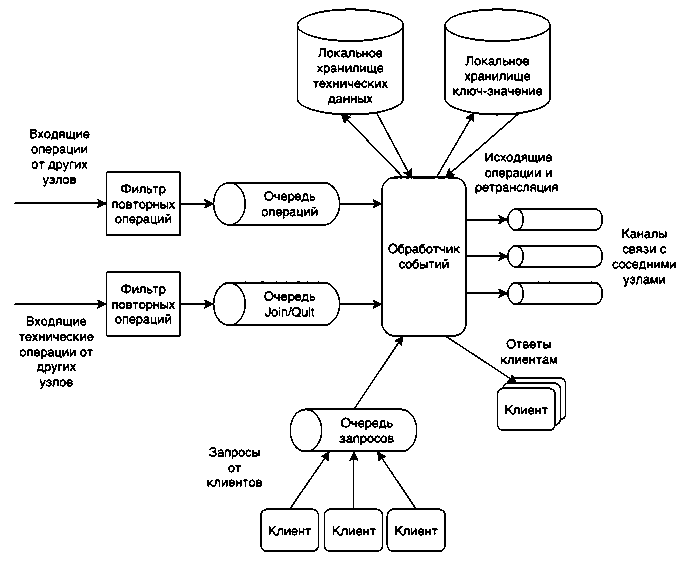
Рисунок 5. Схема взаимодействия компонентов сервиса в рамках одного узла

Разработка частично синхронного консенсусного алгоритма для распределенных систем ...

Распределенное хранилище пар «ключ – значение» может работать как с делением на шарды, так и без него. При делении на шарды повышается пропускная способность сервиса, но возникает проблема с изменением конфигурации кластера. Для ее решения можно применить алгоритм согласованного хеширования. Это предполагает создание зацикленного множества из диапазона возможных ключей, которое разделено на несколько отрезков. Каждому отрезку соответствует токен, за счет которого определяется зона ответственности.

Алгоритм согласованного хеширования обладает такими преимуществами, как равномерное распределение нагрузки при отключении или выходе из строя шарда; возможность иметь виртуальные шарды, которые получают свою позицию на диапазоне и часть ключей, а ответственность делегируется на реальный шард; каждый ключ соответствует точке на диапазоне, после получения точки на диапазоне ищется следующий шард, который и будет ответственным за данный ключ.

Алгоритм позволяет решить проблему изменения конфигурации кластера и обеспечить равномерное распределение нагрузки между шардами. На Рисунке 6 показано распределение ключей по шардам с помощью согласованного хеширования.

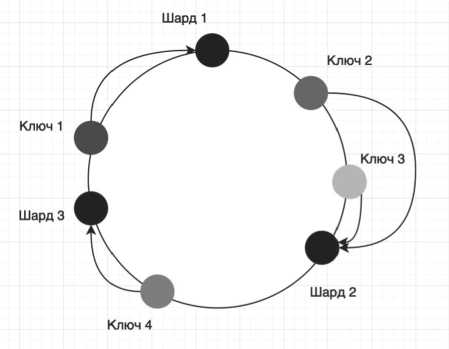
Рисунок 6. Распределение ключей по узлам в зацикленном диапазоне

При выходе шарда или добавлении нового ключи перераспределяется в том диапазоне, где произошло изменение. Это означает, что только ключи, которые были связаны с вышедшим из строя шардом, будут перераспределены между другими шардами. Благодаря тому что остальные ключи не затронуты, операция миграции ключей между новыми владельцами будет достаточно быстрой по сравнению с перемещением всех ключей.

На Рисунке 7 приведен пример перераспределения зоны ответственности при выходе из строя шарда № 2. Как видно, ключи, которые были связаны с шардом № 2, были перераспределены между шардами № 1 и № 3.

Этот подход позволяет минимизировать время простоя системы и обеспечить быструю миграцию ключей между шардами.

Оценка производительности измеряется по количеству операций в секунду для некоторого количества участников сети при наличии задержки между узлами. Все замеры были проведены на процессоре 2.1 ГГц с 4 ядрами и 8 потоками в локальной сети с си- муляцией задержки через таймеры в потоках. Для проверки алгоритма на масштабируемость были проведены замеры для 64, 100 и 144 участников в сети. Для более равномерного распределения нагрузки по участникам сети была выбрана ячеистая топология. Каждый узел имел максимум 4 соединения с соседними узлами. Задержка между соседними узлами составляет 40 мс. Количество операций в пачке от узла равно 10. Размер одной операции: 200 байт – ключ, 200 байт – значение и несколько технических полей. Измерения производились после запуска и определения участников сети.

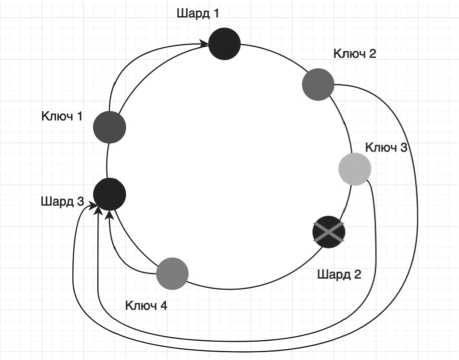
Рисунок 7. Перераспределение ключей

В Таблице приведены результаты замеров. Стоит отметить, что, несмотря на увеличение задержки на согласование раунда, количество операций в секунду при 100 узлах выросло относительно 64, а при 144 узлах незначительно сократилось. Из этого следует, что пропускная способность сети ограничена размером пачки в раунде.

Таблица

Результаты замеров быстродействия системы

Количество узлов в сети	64	100	144
Общее количество операций, сек.	661	736	727
Среднее время на один раунд, сек	0,967	1,358	1,979

Источник: таблица составлена авторами.

Заключение

Предложен алгоритм консенсуса, решающий проблемы необходимости лидера в сети, а также исключающий возможность непосредственно решать порядок операций для любого узла. Для проверки концепции и демонстрации работоспособности алгоритма спроектирован сервис реплицированного хранилища пар «ключ – значение».