Алгоритмическая устойчивость нейронных сетей глубокого обучения при распознавании микроструктуры материалов

Известна проблема подбора обучающего и тестирующего множеств в задачах машинного обучения, к которым также относятся задачи глубокого обучения с целью предсказания физикомеханических свойств функциональных материалов [1–3]. Многие исследователи в области прикладных расчетов используют правило разделения всего доступного множества на обучающее и тестирующее в соотношении 80/20 либо 70/30. Как правило, аргументация такого разделения не приводится. Что касается рекомендаций по объему обучающего множества, то они и вовсе отсутствуют, кроме утверждений, что мощность множества должна быть больше количества параметров нейронной сети в 3–10 раз. Для некоторых сетей существуют теоретически обоснованные оценки. Например, в классической работе [4] приводится примерная оценка количества обучающих данных L для многослойных нейросетей прямого распространения:

L = W/г, где W – количество синоптических связей (весов); ε – ошибка обучения. Например, при ошибке в 0,1 получается правило 10X. В работе [5] для многослойных сетей прямого распространения с одним скрытым слоем приводится оценка величины L в виде

2 (n + m + p) < L < 10 (n + m + p), где n , m , p – количество нейронов во входном, в скрытом и в выходном слоях соответственно. Эта оценка является следствием теоремы существования нейросетей Колмогорова – Арнольда – Хехт – Нильсена [6].

Сегодня глубокие искусственные нейронные сети сверточного типа применяются во многих областях. С помощью миллионов предварительно классифицированных снимков, собранных в массивных базах данных аннотированных изображений, таких как ImageNet или COCO, и метода обратного распространения ошибки удалось достичь действительно впечатляющих результатов [7–9], прежде всего в задачах классификации изображений. Таким образом, начиная с 2012 г. сверточные сети можно считать традиционным методом компьютерного зрения.

Наиболее точной, если не считать малоизученную SENet (Squeeze-and-Excitation Networks), и апробированной сетью является сеть ResNet (Residual Network). Она была предложена в 2015 г. и тогда же победила в ILSVRC. Авторы Kaiming He, Xiangyu Zhang, Shaoqing Ren и Jian Sun заметили, что при увеличении глубины сети ошибка на обучающем и валидационном множестве накапливается [5].

Кроме того, существует проблема оценки качества обучающего множества. Нет четкого ответа на вопрос: насколько ошибочно аннотированные изображения могут повлиять на результат обучения? Например, достаточно часто работу классифицирующей нейронной сети сравнивают с работой человека. Является ли такая оценка справедливой? Ведь обучающее множество содержит аннотированные данные, которые готовились людьми и которые, в свою очередь, содержат те самые ошибки. Насколько эти ошибки могут искажать результат?

Известно, что фундаментальная теория равномерной сходимости В.Н. Вапника – А.Я. Черво-ненкиса [10] трактует фатальные ошибки алгоритма обучения как нарушение алгоритмической устойчивости. Под устойчивыми обучающими алгоритмами понимаются такие, которые формируют только те гипотезы, результат применения которых изменяется незначительно при малом изменении обучающей выборки [11, 12]. В рамках данной теории найдены семейства таких алгоритмов, например, регрессия, метод опорных векторов и т. д.

Обучение глубоких нейронных сетей вряд ли можно проанализировать в рамках теории равномерной сходимости, но численное исследование на устойчивость конкретных сетей может быть вполне доступно. Например, в работе [13] проведено исследование влияния размеров обучающего и тестирующего множеств на точность и обобщающую способность трехслойной нейросети MLP в задаче бинарной классификации. В работе [14] исследуется точность и разброс сети GoogLeNet в задаче классификации частей тела по снимкам компьютерной томографии. Размер обучающего множества подбирается на основании анализа точности результатов обучения. К недостаткам данной работы можно отнести то, что зависимость точности обучения от объема обучающей выборки рассчитывалась на основании 6 численных экспериментов (по каждому из классов), а само тестирующее множество получалось в результате процедуры разделения обучающего множества в пропорции 75/25. Однако если отсутствует устойчивость обучения, то данным результатам вряд ли можно доверять. Кроме того, количество данных для представительности класса можно уменьшить, если использовать предварительно обученные модели [15, 16].

1. Исследование устойчивости

Процесс исследования устойчивости заключался в поиске такой окрестности стабильного решения, при котором происходит нарушение равномерного характера сходимости к среднему. Под стабильным решением понималась обученная глубокая сеть Resnet-152. Сеть обучалась для решения задачи классификации изображений микроструктур по твердости металлического сплава на основе железа. В качестве обучающего множества выступали аннотированные снимки микроструктуры сплавов, примеры которых приведены на рис. 1. При этом микроструктура, приведенная на рис. 1 слева, соответствует сплаву с микротвердостью 1900 МПа, а справа – 7000 МПа. Все исходные изображения микроструктур были разбиты на 14 классов по твердости материала.

Рис. 1. Примеры снимков микрошлифа материала, включенные в обучающее множество Fig. 1. Examples of microsection images of a material, included in the training set

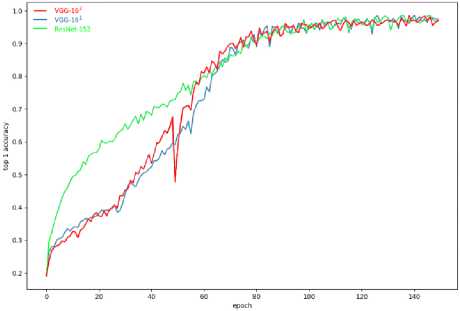
В п роц е сс е об у че н и я с е ти н а 200 -й эпохе была достигнута точность 83,9 % по оценке Top-3, п осле чего в е с а с е ти б ы л и за мор ожены. Оценка точности производилась на ва ли д а ц и он н ом мн о ж е с тв е , с о с тоящ е м и з 10 97 э ле ментов, не предъявленных сети при ее обучен и и . Проц е с с с ход и мост и п о точн ос ти , р а с с ч и та н н ой на обучающем множестве, изображен на ри с . 2.

а)

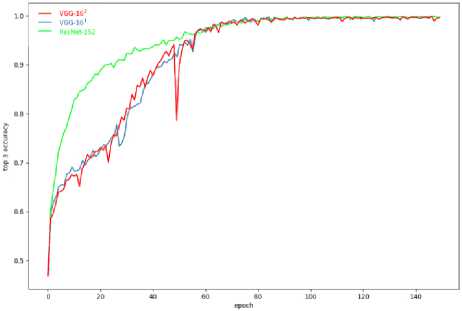
Рис. 2. Точность на обучающем множестве для сетей VGG-161 ,VGG-162 и ResNet-152: а – Top-1; б – Top-3 Fig. 2. Accuracy on the training set for networks VGG-161, VGG-162 and ResNet-152: a – Top-1; b – Top-3

б)

Сеть ResNet-1 52 п ок а зыв а е т высокую скорость сходимости. Практически з а н е с коль к о э п ох была достигнута точность 80 % по Top-3 (рис. 2б). При этом процесс обучения устойчив.

В таб л. 1 п ока за н ы ре зу л ьтаты обучения, выполненные по разным оценк а м, н а об у ча ю щ ем и валидационном множествах.

Таблица 1

Table 1

Результаты обучения сетей

Results of training networks

Сеть	Точн ос т ь н а о б у ча ю щ е м мн оже с тв е		Точность на валидационном множестве
	Top-1	Top-3	Top-1	Top-3
VGG-161	0,9751	0,9975	0,4704	0,8117
VGG-162	0,9712	0,9970	0,5203	0,8142
ResNet-152	0,9593	0,9978	0,6243	0,8933

Определенной неожиданностью стало то, что, несмотря на неустойчивость обучения, непред-обученная сеть VGG-162 показала значительно лучший результат Top-1 в сравнении с предобу- ченной версией этой же сети. Это можно объяснить тем, что первые слои сверточной непредобу-ченной сети смогли лучше приспособиться к специфическим изображениям микрошлифов. Пре-добученная сеть предварительно обучалась на очень большом и разнообразном множестве фотографий. Это улучшило универсальные свойства сети VGG-161 (в особенности ее первых слоев), но ухудшило степень распознавания структур специального вида.

Как и предполагалось, сеть ResNet-152 показала лучший результат – 89,3 % по оценке Top-3. Показанная точность позволяет использовать обученную сеть в качестве ядра интеллектуальной системы комплексного оценивания прочностных свойств функциональных и конструкционных материалов.

Существенное улучшение результатов ResNet-152 было достигнуто при улучшении качества обучающего множества. Из него были исключены образцы снимков с кратностью увеличения x40. Во-первых, их количество было небольшим, во-вторых, снимки с такой кратностью присутствовали не во всех классах изображений. Было сделано предположение, что данные снимки ухудшают результаты обучения. Предположение подтвердилось, так как в результате обучения точность ResNet-152 выросла и достигла величины 92,1 % по Top-3 и 66 , 2 % по Top-1. В табл. 2 представлены точности распознавания по классам материала.

Таблица 2

Точность распознавания по классам материала

Table 2

Accuracy of recognition by material classes

Номер класса	Точность на валидационном множестве
	Top-1	Top-3
0	0,718	1,000
1	0,812	1,000
2	0,593	0,843
3	0,562	0,812
4	0,375	0,937
5	0,937	1,000
6	0,687	0,937
7	0,500	0,933
8	0,562	0,875
9	0,906	0,906
10	0,937	1,000
11	0,375	0,843
12	0,894	1,000
13	0,590	1,000

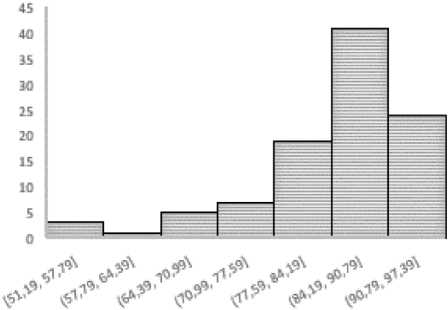
Рис. 3. Гистограмма распределения точности в тестовом множестве

Fig. 3. Histogram of the accuracy distribution in the test set

Лучшая точность по обеим оценкам достигнута в классе 10. Худшая точность по оценке Top-1 получена на классах 11 и 4. При этом по оценке Top-3 на этих же классах достигнута приемлемая точность, которая составила 84,3 %.

Определение точности работы сети по тестовому множеству показало, что плотность распределения точности может быть аппроксимирована распределением Пирсона первого рода, гистограмма которого приведена на рис. 3.

Для изучения устойчивости обученной сети тестовое множество подвергалось вариациям. Окрестность стабильного решения формировалась путем исключения из тестового множества определенного количества элементов. Элементы выбирались случайным образом на 100 реализа- циях. Такую окрестность принято называть Leave-one-out (LOO) окрестностью [5]. Обычно ее глубина равна 1 элементу. В данной работе строились несколько окрестностей: с 2, 4, 6, 8, 10 и 12%-ным отклонением от базового количества элементов в тестирующем множестве, которое использовалось для оценки точности стабильного решения. После прогона и определения точности по всем реализациям в окрестности результирующая точность получалась усреднением. Результаты численного эксперимента показаны на рис. 4.

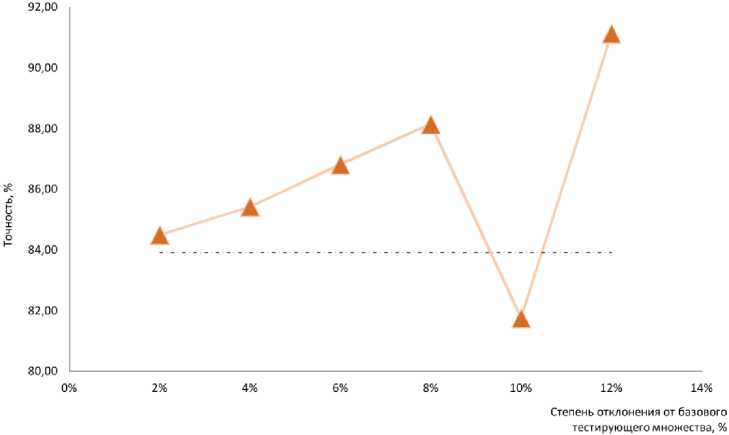
Рис. 4. Зависимость точности обученной нейросети в LOO окрестности базового тестирующего множества Fig. 4. Dependence of the accuracy of the trained neural network in the LOO neighborhood of the base testing set

• 3.    Анализ результатов

Из рис. 4 следует, что процесс проверки обученной сети равномерно сходится к точности, полученной на базовой выборке (обозначена пунктирной линией). При уменьшении количества элементов в тестовом множестве более чем на 8 % происходит резкая осцилляция оценки точности, что, по нашему мнению, является потерей алгоритмической устойчивости нейронной сети в рассматриваемой задаче классификации, которую она решает.

Данное утверждение может быть распространенно и на процесс обучения, так как тестовое множество является независимой случайной однородной выборкой. Если алгоритм потерял устойчивость на тестовой выборке при контрольной проверке точности работы сети, то и процесс обучения сети потеряет устойчивость при уменьшении количества элементов в обучающей выборке на более чем 8 %.

Здесь необходимо отметить, что поиск потери устойчивости процесса обучения в глубоких сетях прямым методом является сложной задачей. Если процесс обучения сети на обучающем множестве размером в несколько десятков тысяч элементов может занимать несколько дней, то исследование устойчивости обучения затруднительно с практической точки зрения. Авторами данной работы предлагается упрощенный подход – исследовать равномерную сходимость на тестовом множестве, после чего распространить полученные выводы на все обучающее множество.

Результат, полученный в данной работе, может накладывать не только количественные, но и качественные ограничения на обучающее множество. Полученный предел может говорить о том, что в обучающем множестве не может быть более 8 % ошибочно аннотированных снимков, иначе процесс обучения потеряет устойчивость и результатам обучения доверять нельзя.

Заключение

В работе изучена проблема равномерной сходимости процесса обучения и оценки точности глубокой сети ResNet-152 в задаче анализа микрошлифов сплавов на основе железа. Показано, что при 10%-ном количественном отклонении в базовом множестве алгоритм обученной сети теряет устойчивость. Это означает, что при таком количестве элементов в тестовом множестве адекватная оценка точности сети невозможна.

Методика оценки устойчивости работы глубокой сети, примененная в данной работе, может быть распространена и на другие сети и задачи. Она не требует объемных вычислений, так как позволяет оценить достаточность количества элементов в обучающем множестве, не выполняя обучения сети на обучающих множествах, имеющих разнообразные мощности.