Алгоритмические решения в задаче оценки информационного воздействия на электорат при проведении выборных кампаний

На сегодняшний день избирательные процедуры – неотъемлемая часть демократических государств. Несмотря на существенные различия исторических путей становления и развития электоральных институтов в различных странах, в настоящий момент содержание избирательных кампаний неизменно базируется на понятиях профессионализма и эффективного менеджмента. Основу для реализации указанных принципов составляет качественное информационно-аналитическое сопровождение выборных кампаний, необходимое как конкурирующим кандидатам, так и организаторам выборов. При этом обеспечение подобного сопровождения с учетом текущего уровня развития систем коммуникации, вычислительной техники и методов математического моделирования [1] невозможно без применения эффективных алгоритмических решений, позволяющих формировать точную оценку информационного воздействия. Основные особенности, которые необходимо принять во внимание при разработке алгоритмических решений в указанной предметной области, связаны с учетом: 1) воздействия средств масс-медиа на избирателей и межличностного взаимодействия; 2) положительного и отрицательного влияния на общественное мнение средствами масс-медиа; 3) двухшагового усвоения информации [5]; 4) наличия многообразия средств масс-медиа, социальных групп и списка кандидатов (партий); 5) cтохастического характера воздействия средств масс-медиа.

Принимая во внимание основные результаты работ [2–6] по математическому моделированию информационного влияния, управления и противоборства в социуме и выделенные особенности, цель настоящей статьи состоит в разработке алгоритмических решений в задаче оценки информационного воздействия на электорат при проведении выборных кампаний.

В

1. Математическая модель оценки информационного воздействия на электорат при проведении выборных кампаний соответствии с [6] электорат представим группой взаимодействующих индивидов численностью Nо, составленной из M подгрупп. Обозначим Nm (m = 1, M) число индивидов в m-й

M подгруппе при Nm < N0, Nm > 1 и £ Nm = N0.

m = 1

Предпочтения у индивидов формируются в отношении K кандидатов с учетом распространя- емой информации через L внешних источников (средства масс-медиа) и за счет межличностной коммуникации. Внешний l-й ( l = 1, L) источник в момент времени t е[0,TQ ] пропагандирует к-го кандидата с интенсивностями а^ (t) и у^ (t), формируя положительное и отрицательное отношение соответственно. Разнородность влияния на m-ю подгруппу индивидов l-го внешнего источника характеризуется коэффициентом восприятия Xml G[0,1] •

Следуя [6], общую группу индивидов разделим на три класса: 1) неохваченные; 2) предадепты; 3) адепты. У неохваченных индивидов отсутствуют предпочтения в отношении какого-либо кандидата.

Предадептами mk назовем индивидов m -й подгруппы, отдающих предпочтение k -му кандидату, но не распространяющих о нем информации при межличностной коммуникации. Число предадептов mk в момент времени t обозначим У тк ⁽ t Ы⁰, N m ] •

Адептами mk назовем индивидов m -й подгруппы, отдающих предпочтение k -му кандидату и распространяющих положительную информац ию в его отношении среди индивидов т ' -й ( т' = 1, M ) подгруппы путем межличностной коммуникации с интенсивностью в m ‘ m >  0. Число адептов тк в момент времени t обозначим x mk ( t ) е[ 0, N m ] • Уточним, что адепт тк в отношении к' -го кандидата ( к , к '^е{ 1, K } ) не распространяет отрицательной информации.

Переход неохваченных индивидов в адепты осуществляется за два шага [6]. Под воздействием положительной информации из внешних источников и за счет межличностной коммуникации первоначально индивид m -й подгруппы становится предадептом тк , а затем - адептом тк • Под воздействием негативной информации из внешних источников в отношении k -го кандидата происходит обратный переход. Уточним, что адептом кандидата может стать только предадепт соответствующего кандидата, а неохваченным индивидом – предадепт.

Для введенных представлений задача оценки сводится к выбору к' -го кандидата, способного по итогам выборной кампании набрать наибольшее число голосов к' = argmax N^, к е[1, K ]

M где Nк = E[xтк (T0 ) + yтк (T0 )]

т = 1

Ее решение требует максимально правдоподобно- го определения числа адептов хтк (t) и предадеп-тов yтк(t) •

Для заданного содержательного представления математическую модель сформируем, принимая во внимание основные предположения о скорости изменения х_т к ( t ) , у_т к ( t ) [6] и допущения.

• 1.    Значения х т , в _т - _т не зависят от t и определяются экспертным оцениванием.

• 2.    Переменные х_т к ( t ) , у_т к ( t ) составляют непрерывный векторный марковский процесс.

• 3.    Интенсивности а к1 ( t ) , у ^ ( t ) складываются из соответствующих истинных значений 0 <а 0 1 ( t ) , у 0 1 ( t ) <« и ошибок наблюдения а ^ ( t ) , у к1 ( t ) , являющихся белым шумом с соответствующими характеристиками: Е [а ^ ]= Е [у к1 ] = 0; ^{cov [а} н ^] = ^cov Л н ] = ⁵ ( t ^-т ) ; ^{cov [} d ^а н ] = ^[е и ] ; ^{cov [} d ^Y н ^] = ^[sY i ^] •

Для заданных представлений решение задачи оценки x_т к ( t ) и у _т к ( t ) выполним усреднением:

Z (t ) = JZ p (Z, t) dZ, Q где

Z = ( Z ) d = ( f W..... z < M ) ^ ;

: ⁽ " > -( « к^т * 1   = ( Хт „У т ,

V 72 K

•, ^ХтК ,

^утК ) ^;

Q = Б^{( 1 )} X ••• Х£⁽ M ) с К d

d -мерный выпуклый

многогранник (d = 2MK); s(т) с К2К симплекс

с 2 К +1 вершинами Р( т ) = ( 0,0V„, 0), P2 т ) = = (Nm,0,•••,0), ", P2K+1 = (0,0,•••,Nm ); p(Z,t) -функция плотности распределения вероятности, удовлетворяющая уравнению Фоккера – Планка – Колмогорова (ФПК):

dp ( Z, t ) Idt = L [ p ( 'Z, t ) ] ,

где

L [ p ] = -Ei(A.p) +1E E l=1dZl           21=11 '=1 dZldZl'

• - диффузионный оператор; D = ⁽ D ll ') d X d и A = ( A l ) d - тензор диффузии и вектор сноса соответственно, компоненты которых формируются из следующих представлений:

• 1) для вектора сноса:

  -             ( : ( 1 )     : ( M ))

A = ( A ,). = a ,•••, a ;

^l d V                  J

im)-fa(m))   -f/1)/2)

a “I a i    I “I f m 1 , f m 1

V     72 K  V

f ( 1 ) /²) \ ^fmK , ^fmK I ;

предлагается выполнять численно в соответствии со следующей схемой.

f m ^^X> ^Y > t ^{) = (} x mk - У тк ^)r mk +

+

0 mk

M

⁺ / ’ x m ' к ^в m ' m m '“ 1

x

2. Численная оценка информационного воздействия на электорат при проведении выборных кампаний

K

Зададим разбиение Q=

U

U «< u >

набором из U

u = 1

симплексов

N m - h ⁽ x mk ' ⁺ y mk ' ) - y mk к '“1

;

fi.^ X Y, t ) = ymk Amk+ M         " / ’ xm' k в m' m xmk Г 0 mk L 00 Г mk /

to

, ,      f d+1 / \ / \ f d +1

■^{1 u}Mh-^(u)Pi^u): h-

11=1               V l=1

aTvI = 1, d +1, -^(u)

V

•( u ) l

■■ Г

)

=1 a

d

(u = 1, U) с d +1 вершинами P(u), P2⁽u),

…,

u

^d+) и

⁽mm') kJ • V ii

A /уml^ekl ) , v i=1

if m = m' л imod2 * 0 a i = i';

.«

ymk. ^^(xmlEkl) ,

if m = m ' л i mod 2 = 0 л i = i';

= <

⁽xmk

-

L₂ ymk L h^(xml^ekl ) ^,

if m = m'aimod2 * 0лi-1 = i';

K

Nm — h ⁽xmk' ⁺ymk' ) - ymk k '=1

L h(xml«a), l=1

x

if m = m 'a i mod 2 = 0 л i -1 = i';

0, otherwise.

Решение дифференциального уравнения (2) при заданном начальном условии p (Z, 0) и требований p (Z, t )>0, J p (Z, t) dZ = 1 для (Z, t )eQxr0, T_Q ]

Q

r (u)

барицентрическими координатами -1 ' (u) _ (u')

при to Oto =0 I u * u; u, u = {1, U}).

Обозначим ^-,-^q скалярное произведение

r^(u)

^Zd+1

( П, Ф^=/п( Z )ф( Z) dZ                           (3)

Q

для некоторых функций n и ф.

Зададим аппроксимацию p (Z, t):

Р (Z, t )=E h c (u *( t )4 ’(Z),                   (4)

u=1 jeMd

подстановка которой в (2) в проекционном представлении метода Галеркина сведет исходную к системе обыкновенных дифференциальных уравнений:

d<5 (t)/dt = S-1Q (t) <5 (t);   <5 (0 ) = S-W, где i f(u)\ )

^W = I\p0, vj      I ;

^V'         '^q7u| Md

p 0 = p⁽Z,⁰)^;   C = ^fcj¹ )1

^{v   7}u md

– вектор искомых коэффициентов разложения, зависящих от t;

n f/ (^u) T Г (^u')1\

Q = j L V j

V L     J/^qJu| Md IxulMd

Md - множество мультииндексов j, j' е Мr [8]:

Мd = Ь = (ji,...,ji,..., jd+i): ji е^+,

1         .(6)

Z i е[1; d+1]

ее наилучшее среднеквадратичное приближение с коэффициентами разложения Cj. Тогда справедлива оценка

II^n-nrl Ito⁵M2

II4/^r⁷¹,

где M₂– не зависящая от r положительная постоянная.

где r е N - порядок аппроксимации на to

В формулировке леммы 2 для

₊ = N ^u{o}; V") — базисная функция частичной

to =

подобласти to⁽") eQ, которую зададим произведе-

k+1       Z к+1

ZZkPk^:ZZk =¹ k=1        \ k=1

A

нием:

d+i v ju 472/^(r+1)Пф^ i=i

a(v k = 1, K +1,

^Zk²⁰)[

G К^K,

Гауссовых базисных функций [9]:

_m -[2jl +1-2Z i (r+1)J2 /[²( d+¹)] ^фji = e                              .

Решение (5) определяется в виде

C (t) = exp

t

S^-1jQ (t) d т

S A,

r е N, j е M^к приняты обозначения:

к+1 ^хП^e k=1

to

11-Z1

X

;

для

к-1 1-ZZ_; k=1

где exp ^-J - матричная экспонента.

Сходимость решения (9) задачи (2) в проекционном представлении (5) с учетом известной, например из [10, с. 80], теоремы Л.В. Канторовича

составляет последовательное исследование задач приближения непрерывной функции на [0,1J и to⁽") Гауссовыми базисными функциями вида (7), (8).

Лемма 1. Пусть n(Z) - непрерывно дифференци-r руемая на [0,1J функция, а n (z) = Z cФj (Z) “ ее j=0

наилучшее среднеквадратичное приближение с коэффициентами разложения c_j . Тогда справедлива оценка II^n-nrll[0,1J- ^M1IH[0,1]/^, ⁽¹⁰⁾

(n,ф)_to⁼j j ... j n(Z)ф(Z)dZ_K...dZ₂dZ1 000

K при ^ZK+1 = ^{1 -}Z^Zk. k=1

Из результатов лемм 1, 2 получено следующее утверждение.

Теорема 1. Пусть

P (Z, t )=Z Z c (u)(tH")(Z), u=1 jeM d тогда метод Галеркина для уравнения (2) сходится и справедлива оценка

где M₁– не зависящая от r положительная посто-

янная.

В формулировке леммы 1 для Z е [0,1], r е N приняты следующие обозначения:

где M₃– не зависящая от r положительная постоянная, и - максимальный линейный размер симплек-

(u) сов to

.

ф j (Z) = 2- (r +1) e' '²

⁽j = °, .);

II ^П[0,1]=/^п, ⁿ[0,1J

при Z*^0,1J = jn(^Z)*(^Z)^dZ.

Лемма 2. Пусть

n(Z) - непрерывно дифферен-

цируемая на to функция, а i](Z)= ZCjVj (^z) -

7еМ K

3. Алгоритмическая реализация решений в задаче оценки информационного воздействия на электорат при проведении выборных кампаний

Основу алгоритмической реализации сформированной численной схемы составляют:

1) построение d-мерного выпуклого многогранника Q при формировании множеств его

• 1:    function VehtPoly(^ M, K)

• 2:    for m = 0 to M — 1 do

• 3:      y_m = PlacePol\t(2K, W_m+i);

• 4:        jm⁼ 0;

• 5:    repeatv = 0

• 6:      for m = 0 to M — 1 do

• 7:          ^v = vU(v_m)_Jm;

• 8:         V<= v;

• 9:   until NextPlacementO, 2K, M - 1);

• 10:    return V

• 1:    function PlacePol\t(K, N)

• 2:    for к = 0 to К — 1 do

• 3:          (v₀)_fc = 0;

• 4:    for к = 1 to К do

• 5:          Vfc = Vo;

• 6:         (Vk)fc_i = A ;

• 7:    return V

Рис. 2. Псевдокод функции PLACEPOINT

Fig. 2. Pseudocode of the PLACEPOINT function

Рис. 1. Псевдокод алгоритма формирования V

Fig. 1. Pseudocode of the V formation algorithm

l-мерных граней (вершин V, ребер E, граней B⁰, ячеек B¹ и пр.);

• 2)    разбиение Q = |^J®⁽u) на симплексы ю⁽u); u=1

• 3)    правила вычисления элементов вектора W,

т       т  Т    Т матриц Q, S и усреднения Z (t) = I Zp (Z, t)dZ,

Q уточняемые реализацией процедуры численного

• 1:    function NextPlacement(j, K, M)

• 2:    г = M;

• 3:    while (г > 0) Л (jj = K) do i = i — 1;

• 4:    if г< 0 then return false;

• 5:     if ji > К then 2 = -i — l;

• ^6:     ji ⁼ ji + 1;

• 7:    if 2 = M then return true;

• 8:    for к = г + 1 to M do jk = 0;

• 9:    return true

Рис. 3. Псевдокод функции NEXTPLACEMENT

Fig. 3. Pseudocode of the NEXTPLACEMENT function

интегрирования по Q.

Известно из [11], что количественная характеристика l-мерных граней (l = 0, d -1) Q определяется f- и h-векторами, соотнесенными с F- и

H-полиномами. Исходя из правила

• (1)         ( m )

Q = 8 x... x8   c Rd 2K-мерными

• (m)

ми 8  , справедливо представление

построения симплекса-

F-полинома

8(m)

в виде

h-вектора, определяемые суммами мультимодальных коэффициентов из (13) по правилу:

h(q)= E f M     ^,                (14)

q^MMK Vq1,q2,...,q2K+1 J sq =1

где ^sq = Z (^{k +}1) qk+1.

kel" 1;2 K "I qk+1 *0

F

2K f 2 K +1

k +1

т ^k

Элементы Д (q) f-вектора вычисляются из (14) выражением [11]

а H -полинома:

fi‘A fl Q   z i hl (Q).

2K mm

H 8⁽), т = F 8⁽), т-1 = > т^k.

^{X ; X           ;} k =0

l '=l V J

Тогда H -полином Q, с учетом обобщения бинома Ньютона при введении мультимодальных коэффициентов, задается соотношением

f 2 K  AM

^H (Q т)= £т ^k

V k=0   J

z qeMM "V

M

^q1, ^q2,..., ^q2 K+1

2K

Пт qk-1

^Jk=0

d

= Zhl (П)т*.

l=0

Здесь MM - множество мультииндексов q, заданное по аналогии с (5) (быстрый алгоритм формирования Мd приведен в [12]); hi (q) - элементы

С учетом заданных количественных характеристик Q выполняется формирование множеств его l-мерных граней. При этом изначально задается множество вершин V с числом элементов f 0 (Q) = |v| = (2K +1)M - алгоритм VERTPOLY (рис. 1).

Основу работы алгоритма составляют функции определения множества исходных точек PLACEPOINT (рис. 2) и задания нового размещения с повторением NEXTPLACEMENT (рис. 3) [13].

Затем определяется множество ребер E c V x V с числом элементов f1 (q) = E| = (2K +1)M KM, составляемых комбинацией пар неповторяющихся вершин V – алгоритм EDGEPOLY (рис. 4).

Множество граней B⁰ с числом элементов f 2 (Q) = B0| формируется по заданным V и E при представлении Q в виде неориентированного

function EdgePoly(V, M, K)

2: 3: 1: 6: 7: 8: 9: 10: 11:	for п = 0 to |У| — 2 do for 7?/ =s n + 1 to |У| — 1 do г = 0; for m = 0 to M — 1 do jm= 0; for к = 0 to 2K — 1 do if ^Ti^mK+k Ё ^^ImK-Vk fhenjm = jm + К if jm > 0 then z = i+l; if (^ < 1) V (M = 1) then j _ v^M-l . . — Z^m=0 Jm i
12: 13: 14:	if J < 2K then E 4= (??. n')T; return E

Рис. 4. Псевдокод алгоритма формирования E

Fig. 4. Pseudocode of the E generation algorithm к function SearchCycles^VjB)

• 2:    while true do

• 3:      D = KirhgofMai kix^, V);

• 4:         r = 0;

• 5:        for г = 0 to |V| — 1 do

• 6:          if Da > 1 then

• 7:             £'= MST(D, V,i):

H:             if E' ^ T then

• 9:                 Т_т = E'; г = r + 1;

• 10:       if r — 0 then break:

• 11:        E' = 0:

• 12:       for г = 0 to J — 1 do

• 13:          E' = E’ U Td

• 11:         Ё = Е\Е:

• 15:           for nV = 0 to 1 do

• 16:               Ё = Tf.

• 17:               for n = 0 to |Б| — 1 do j_n = 71 + 1;

• 18:              repeat

• 19:                 for m = 0 to m' do £|r. |_|__m = Ej_m_^

• 20:              c = DFSCycle^, V,Ly,

• 2. 1:                   if с ^ C then

• 22:                       C<= c:

• 23:             until Nex i Combination^, г + 1, |5|):

• 24:       E = E\E'-

• 25:    return C

Рис. 5. Псевдокод алгоритма поиска циклов для G длиной L

Fig. 5. Pseudocode of the loop search algorithm for G of length L графа G (V, E) = ^V, E^ и последовательном поиске в G всех циклов без хорд длиной L = |^3; 4] . Полиномиальный алгоритм поиска циклов базируется на алгоритмах построения остового дерева (алгоритм Прима [13] – MST) и рекурсивного поиска в глубину [13] – DFSCYCLE. Алгоритм поиска циклов SEARCHCYCLES для G длиной L приведен

на рис. 5.

В алгоритме поиска циклов используются дополнительные функции построения матрицы Кирхгофа KIRHGOFMATRIX для G и задания но-

вого сочетания без повторения NEXTCOMBINATION (рис. 6).

Множество ячеек В¹ с числом элементов f 3 (q) = = |в1| формируется по В⁰. Каждая грань представляется бинарным числом разрядностью, равной мощности множества E. Разрядом числа кодирует содержание соответствующего номера ребра из E: значение 1 характеризует наличие данного элемента в грани, значение 0 – отсутствие. Затем выделяются ячейки при определении сочетаний 4, 5 и 6 граней из общего числа:

• 1:    function NextCombination (j, m, n)

• 2:    к = m;

• 3:    for i = к — 1 to 0 do

• 4:       if jj < n — к + i + 1 then

• ^5:             jt = jt + 1;

• 6:           for i! = i + 1 to к do jv = jv-i + 1;

return true;

• 7:    return false

d

X⁰= X Хх (l = 1, d);

jl           jljk

/ k=1

Xi (i=1 I)

– корни многочлена Лежандра первого

* рода порядка I [14]; B =

при

Рис. 6. Псевдокод функции NEXTCOMBINATION

Fig. 6. Pseudocode of the NEXTCOMBINATION function

⁽bj) м i|

d bj=ПГ( X -I+

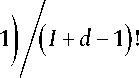
• 1)    4 граней, составленных только из 3 ребер;

• 2)    5 граней, где четыре составлены из 3 ребер, а одна – из 5;

• 3)    5 граней: две составлены из 3 ребер, а три – из 5;

• 4)    6 граней, составленных только из 4 ребер.

Критерий в определении ячейки состоит в том, что сумма по модулю два всех двоичных чисел составляющих граней равна нулю.

Дальнейшая процедура формирования l-мерных граней выполняется по индукции.

Для П симплексы to^(и) задаются при построении барицентрической триангуляции, которая реализуется индукцией по размерности триангуляцией l-мерных граней [11].

U (и)

С учетом разбиения П = ^ to интеграл

и обозначении гамма-функции г(•);

d          jk

^O"(OH')мdPIмd| ^{при 0}"'=П⁽Xjk) ■

Заключение

Таким образом, в настоящей статье в развитие моделей [2–6] информационного влияния, управления и противоборства в социуме при формализации содержательной постановки задачи, выделении системы ограничений и допущений, разработке математической модели, численной схемы и алгоритмических реализаций сформиро-

I = Jn( Z) dZ n

u=1

по П от некоторой функции n за-

меняется суммой I =

U                   (u)

^ J n(Z)dZ по ^ю' исво-

вано алгоритмическое решение в задаче оценки информационного воздействия на электорат при проведении выборных кампаний. Математическая модель базируется на обобщенной модели информационного противоборства в структурированном социуме [2–5]. При разделении общества численностью N₀ на M подгрупп и введении сто-

U=1 ( u) to дится к реализации процедуры численного интегрирования:

I^(u) = J n(^Z)^dZ = ^ n(^j)^кj, to^(u)              jeMI

где I e N - порядок численного интегрирования; узловые точки *j и весовые коэффициенты кj, вычисляемые по правилам кубатурных формул для симплексов. Для мастер-элемента to единичной размерности значения *j eto и кj определяются по правилам:

хастических компонент данная модель сводится к стохастическому дифференциальному уравнению, которое при понимании в смысле Ито [7] приводит к необходимости решения уравнения ФПК (2) для определения эволюции функции плотности вероятности p (Z, t). Решение (2) предложено выполнять численно в проекционной постановке метода Галеркина при задании кусочно-полиномиальной аппроксимации (4), требующей разбиения области анализа П на симплексы to^(и). Для сфор-

мированной численной схемы определена оценка сходимости (12) и уточнены особенности алгорит-

н X0. - X0d )T;  к=0-1B, где

мической реализации, сводящиеся к построению

П, его разбиению П =

U и to(u)

и уточнению реали-

u=1

зации процедур численного интегрирования по П.