Алгоритмическое и программное обеспечение процесса культивирования сине-зеленых микроводорослей в пленочном биореакторе

Одной из важнейших задач комбикормовой промышленности является выработка продукции, которая сочетала бы в себе одновременно низкую цену и гарантированно высокое продуктивное действие. Этим требованиям в полной мере отвечают природные биологически активные добавки – суспензии синезеленых микроскопических водорослей (хлорелла, спирулина и др.). Их действие основано на естественном сочетании природных стимулирующих и биологически активных веществ, выделяемых клетками в культуральную среду (суспензию). Ранее стимулирующий эффект микроводорослей не использовался вследствие скармливания их в виде пасты или порошка. Получаемая белково-углеводная масса является трудноусвояемой из-за значительной толщины клеточных стенок (до 1 мкм при диаметре клетки 1,5…10 мкм), для разрушения которых требуется термическая обработка, повышающая энергозатраты и снижающая биологическую ценность продукта.

Поэтому перспективным является использование суспензии сине-зеленых водорослей, содержащих аминокислоты, витамины, ферменты и другие вещества, выделение которых клетками наиболее интенсивно в начальном периоде роста.

Получение суспензии целесообразно осуществлять в биореакторах пленочного типа, в которых она стекает по внутренней поверхности цилиндрических прозрачных трубок с одновременным подводом углекислого газа и световой энергии [1].

Нами разработан экспериментальный биореактор, позволяющий осуществлять процесс культивирования суспензии микроводорослей в широком диапазоне изменения технологических параметров [5, 7].

Цель исследований – выбор рациональных технологических и геометрических параметров биореактора методами математического моделирования.

Математическая постановка задачи моделирования определялась однопараметрической диффузионной моделью [2, 3, 4], учитывающей в общем случае распределение компонентов питания и микробных клеток по высоте трубок пленочного биореактора, основным параметром которой является коэффициент продольного перемешивания или критерий Пекле

Pe = WH / D _h , где W - средняя скорости течения пленки; H -высота аппарата; D _h - коэффициент диффузии.

При этом предполагалось, что радиальное перемешивание среды в колонне незначительно и концентрация вещества является непрерывной функцией пространственной координаты. Для установившегося процесса в биохимическом реакторе модель представлена в следующем виде:

D h dC - WdC ± tR ( C ) = 0,   (1)

dz2 dz с граничными условиями третьего рода на левой границе участка z = 0: WC0 = WC—DH —, 0 Н dz z = Н : — = 0, dz где (+) - относится к «источнику», (-) - к «стоку»; C - концентрация распределяемого ве- щества; t - среднее время пребывания сус- пензии в аппарате; R(C) - скорость потребле- ния вещества из среды в процессе биосинтеза.

Предложено рассматривать распределение концентрации абсолютно сухой биомассы суспензии в безразмерном виде вдоль одномерной области:

1 d ² x dx -      „ _2x a

--5----+t (ex — fix ) = 0 , (2) Pe dZ2 dZ где £ - коэффициент скорости роста культуры; в - кинетический параметр; с граничными условиями:

Z = 0:

1 dx

Pe dZ

Z = 1: dx = 0, dZ

где x - безразмерная концентрация распределяемого вещества, x = C / C0; Z = z / Н - без- размерная пространственная координата.

Нами было использовано сочетание метода конечных элементов и метода Галёркина [6] для решения дифференциального уравнения (2) с заданными краевыми условиями задачи (3) - (4). Это позволило получить приближенное решение дифференциального уравнения (2) при выполнении условия: разность между приближенным и точным решениями должна быть ортогональна функциям, используемым при аппроксимации [6].

В соответствии с [6] представим дифференциальное уравнение (2) в неявном виде:

Lu — f = 0, где L - дифференциальный оператор, а приближенное решение найдем по формуле u = Е NU i , тогда

Lu — f = § , где § - ошибка результатов моделирования.

Для получения минимального значения § для каждой из базисных функций N i , ортогональных ошибке по области R , требуется выполнение равенства

J N i § dR = 0.         (5)

R

В соответствии с методами Галёркина и конечных элементов получили уравнения в виде

J N p L { ф } dR = 0, в = i , j , k ,...,   (6)

R где ф - искомая величина, которая аппрокси- мируется соотношением ф = Nфl+ N^j=\. N ]{Ф},   (7)

где    [ N ] = [ N i N j ]   - матричная строка;

{ Ф } =

' Ф/'

Ф

вектор-столбец.

Высший порядок производных в L(ф) не ограничен и на единицу больше порядка не- прерывности интерполяционных соотношений. Поскольку рассматриваемые интерполяционные соотношения (7) нулевого порядка непрерывности (непрерывна ф, но не ее первая производная), то в уравнения (6) включены производные порядка не выше первого. Это ограничение может вызвать сложности построения алгоритма, которые преодолены сокращением порядка L(ф) , интегрированием по частям.

Для решения модели объекта исследования (2) - (4) методом конечных элементов задана система дифференциальных уравнений в частных производных. Для упрощения описа-

Г [ N ( e ) ] d' x dZ = [ N ( e ' ^ — Le / ^J zz ^{2 L J} zz

-

T dx ^Zj

_f ZN ⁽ e ) dx dZ dZ dZ

L ⁽ e )

-

Z . (13)

ния алгоритма расчета уравнение (1) шем с заменой переменных d2 x    dx

—х - a--+ bx = 0

dZ2 dZ с граничными условиями

перепи-

Z = 0:

Z = 1:

dx

—=A; dZ dx

= о , dZ

где a = Pe ; b = Pe t £ ; A = Pe x ₀.

Применение метода Галёркина к дифференциальному уравнению (8) заключалось в решении интегрального уравнения

j [NI

о

1T [ d

dx I a—Z + bx ) J dZ = 0. (11)

Интерполяционная функция для x определена на отдельном элементе, поэтому уравнение (11) записано для суммы

NE         T

X j [ N(e) ]

e = 1 L e )^L

² d ² x ⁽ e )

—/

--------1

dx ⁽ e e a

[ ZZ

\

ZZ = 0, (12)

+ bx ⁽ e ) )

J

где NE - число элементов; L ^{( e} )_- длина от-

дельного элемента.

Для вычисления выбраны функции формы и преобразован интеграл (12) таким образом, что он содержит производные порядка не выше первого.

Ограничимся линейной моделью для x x = NX, + N j X j =

( 7 A 7 | 1 - Z I , Z . [ L J L

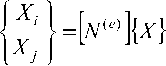
интеграл

j [ N ^{( e} ) ] L < ^e >

] d2x dZ dZ

преобразуем путем интегрирования по частям

Подставляя (13) в (11) и группируя подобные члены, получаем

T dx ^Zj

Г N ⁽ e ) ] T dx

L ] dZ

Zi

- j

L ⁽ e )

d [ N(e) ] ]

dZ

+ а Г N(e) ] ]

dx

—dZ + dZ

+ b j Г N ^{( e} ) ] T xdZ .                    (14)

L < e ) ^{L ]}

Сумма интегралов в (1.14) представляет собой матрицу коэффициентов элемента [ k ^{( e} ) ] в уравнении

[ k ( e ) ]( X } = { f ( ^e ) } .

Первое слагаемое в выражении (14) соответствует вектор-столбцу { F } и определяет производную dy / dx (наклон) на каждом конце конечного элемента. При неизвестном наклоне элемента в узловых точках первое слагаемое в (14) не учитывается.

Вычислим производные в выражении первого интеграла (14):

А [ N ] ] = d Г - L [ = 1 I ^-Ч, dZ dZ Z L [ 1

. L

dx dZ

—{ n }{ x } = -[ - 1;1] J X | , dZ ^{L И J} L       [ X J J

и после подстановки получим

L

j [ dZ [ ^N ] T + a [ N ] T

1 a

L 2

1 a

L 2

dx

— ZZ = dZ

-+-

L 2

1 + -

L 2 ]

i

Вычислим второй интеграл в (14)

b j [N]T xdZ = b j [N]T xdZ =

L^e )                     L^e )

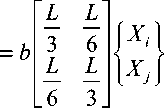
; 0' 1 - L	A +	L x2 1 -	1 • 0 -	[ L	a ^^^^^™  ^^^^^^^^^^e 2
0		X.		1	a ^^^^^s  ^^^^^^^^^^.
. L .		. L		_ L	2

1 a

L ⁺ 2 { X 1 1 +

L₊a J. X ²

L

+ b ³

L

L

Верхние индексы отброшены, так как рассматривается отдельный элемент. Интегрирование выполняется в пределах от нуля до L, так как функции формы в (5) выражены в местной системе координат с центром в i - м узле, L - длина элемента.

Алгоритм решения задачи моделирования (8). Разобьем аппарат по длине на NE = 5 элементов (рис. 1), построенных на множестве узлов Q :{ X 1 , X ₂,..., X ₆},

^^^^^^B

L

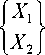
= 0

Для элементов n = 2,..., NE :

L

L

a

2 a 7

1 a

---+

L 2

1 a

— + —

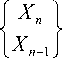
+ b

L

L 2

3 L

L 6

L б" L

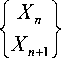
= 0

X i = ( i - 1) • L , i = 1,..., NP , NP = NE + 1, L = 1/ NE . Пронумеруем элементы и узлы таким образом, чтобы каждый элемент e был ограничен сверху узлом i , а снизу - узлом j , причем i <  j .

Объединим матрицы элементов, получим систему линейных алгебраических уравнений:

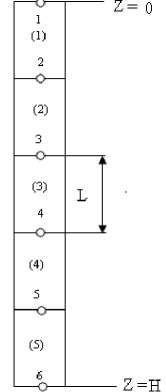
Рис. 1. Область перемещения суспензии сверху вниз: в скобках помечены номер конечного элемента, цифрой (помечен) - узел

(1 a bL ) -  + + k L 2 3 )		1+	(1 k L	a - +• 2	bL2 6j	| u 2	- A = 0;
(1 a bL Л k L + 2 + 6 j	| u 1	+("	2 ^^^^. ^^^^^^^™ L	2 bL + 3	j u 2	+(	1 a bL' L " 2 + T.	j U 3 = 0
(1 a bL Л k L + 2 + 6 j	| u 2	+(	2 - L	2 bL + 3	| u 3	+(	■ 1 - a + bL . L 2 6,	j u 4 = 0;
(1 a bL Л k L + 2 + 6 j	| u 3	+(	2 ^^^^^ ^^^^^^^. L	2 bL + 3	^ " 4	+(	' 1 a bL . "l" i+T.	) u 5 = 0
(1 a bL Л k L + 2 + 6 j	| u 4	+(	2 - L	2 bL + 3	| u 5	+(	1 a bL . L ” k+T	) u 6=0;
(1 a bL Л k L + 2 + 6 j	| u 5	+1	1 ^^^^^ ^^^^^^^^ L	a —+ 2	bL 3	j u .	= 0.	(15)

Тестовый пример. Для случая a - 4 b > 0 найдено точное решение задачи (8) - (10) для а = 1,1; b = 0,264; A = 0,055:

x ( Z ) =

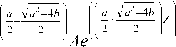
Рассмотрим систему уравнений для первого элемента. Из (9) известны значения про-

2 e

+

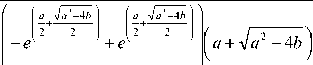
dx изводных фикции x в узлах 1 и 6 — dZ

= A и

X 1

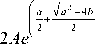
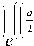
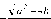
dx dZ

= 0. В других узлах значение производ- X 6

ной неизвестно, поэтому в них не указывается значение производной, а система уравнений для первого элемента в матричной форме имеет следующий вид:

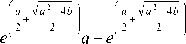
V a ² - 4 b - e

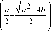
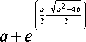
V a ² - 4 b

Решая систему (15), получаем значение концентрации в узловых точках u i , i = 1^6. Текст программы представлен на рис. 2.

• >    restart;

Число элементов

• >    NE:=15;

NE:=15

Число узлов

• >    NP:=NE+1;

NP:=16

• >    PR_MKE:=proc(PE,tcp,epsilon,x0,N)

• >    local a,b,A,u,ur,i,n,L,SYST,PER,rez,Z,U,dr0,drk;

• >    global S;

• >    L:=1/N;

• >    a:=PE;

• >    b:=PE*tcp*epsilon;

• >    A:=PE*x0;

Система алгебраических уравнений

• >    ur[1]:=(-1/L+a/2)*u[1]+(1/L-a/2)*u[2]+b*L/3*u[1]+b*L/6*u[2]-A;

• >    for n from 2 to N-1 do

> ur[n]:=(1/L+a/2)*u[n-1]+(-1/L-a/2)*u[n]+b*L/6*u[n-1]+b*L/3*u[n]+(-1/L+a/2)*u[n]+(1/L-a/2)*u[n+1]

+b*L/3*u[n]+b*L/6*u[n+1];

• >    od;

• >    ur[N]:=(1/L+a/2)*u[N-1]+(-1/L-a/2)*u[N]+b*L/6*u[N-1]+b*L/3*u[N];

• >    SYST:={seq(ur[n],n=1..N)};

• >    PER:={seq(u[n],n=1..N)};

• >    rez:=fsolve(SYST,PER);

• >    for i from 1 to N do

• >    Z[i]:=(i-1)*L; od:

• >    for i from 1 to N do

• >    U[i]:=subs(rez,u[i]); od;

• >    dr0:=(U[2]-U[1])/L;

• >    drk:=(U[N]-U[N-1])/L;

• >    printf(" xn= %10.5f A= %10.5f dr0= %10.5f drk= %10.5f \n",U[1],A,dr0,drk);

• >    S:=[seq([Z[i],U[i]],i=1..N)];

• >    end proc:

• >    # PE tcp epsilon x0 N

• >    S1 :=PR_MKE(1.1,10,0.3,0.05,100):

xn= 0.00501 A= 0.05500 dr0= 0.05522 drk= 0.00082

• >    plot([S1]);

Рис. 2. Текст программы в языке символьных вычислений Maple

Результаты расчета представлены в виде кривой на рис. 3.

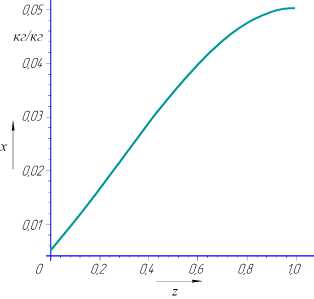
Рис. 3. Расчетная кривая изменения концентрации суспензии по высоте трубки

Из рис. 3 видно, что значение концентрации абсолютно сухих веществ суспензии увеличивается при течении суспензии сверху вниз к нижней точке прозрачной трубки био- реактора.

Результаты расчета методом конечных элементов оценивались средней ошибкой ап- проксимации:

100 ⁿ

Xi - Xi xi

Ac =  Z n i=1

где x i , x i – точно вычисленное по формуле (16)

и вычисленное по методу конечных элементов значение концентрации; n – число узлов конечно-элементной модели.

При NE = 5 средняя ошибка аппроксимации вычисленной концентрации составила 2,2 %, а при NE = 10 – 0,04 %.

Предлагаем метод моделирования процесса культивирования сине-зеленых микроводорослей, основанный на математической интерпретации концентрации абсолютно сухих веществ суспензии при ее росте по высоте прозрачной трубки в пленочном биореакторе совместным сочетанием методов Галёркина и конечных элементов. Идентификация параметров предлагаемой модели по экспериментальным данным позволила получить удовлетворительную сходимость результатов моделирования и использовать их для определения геометрических размеров биореактора.

При решении задачи моделирования был рассмотрен линейный одномерный симплекс-элемент. Для повышения точности решения потребуется другой подход, который состоит в применении элементов высокого порядка, то есть комплекс или мультиплекс элементов, требующий меньшее количество элементов. Это могут быть квадратичные и кубические элементы [6], что будет следующим этапом при моделировании исследуемого процесса.