Алгоритмическое и программное обеспечение решения конструктивной задачи управления неголономными пятимерными системами

Одной из важнейших задач робототехники и инженерии является задача перевода механической системы в требуемую конфигурацию. Например, это может быть вывод спутника на орбиту, управление мобильным роботом, вращение твердого тела в руке робота-манипулятора и многое другие. В математике подобная задача формализуется как конструктивная задача управления. Имеется динамика механической системы, описываемая системой дифференциальных уравнений с функциональными параметрами (управлениями). Требуется найти управляющие воздействия в заданном классе функций, при применении которых система переходит из начального состояния в заданное целевое состояние.

Работа поддержана Российским фондом функдаментальных исследований, проект 12-01-00913-а.

○c А. П. Маштаков, 2012

○c Программные системы: теория и приложения, 2012

В работе рассматривается двухточечная задача управления следующего вида:

q = U i (t)X i (q) + U 2 (t)X 2 (q),

q(0) = q0, q(T) = q1, где пространство состояний Q Э q — это связное пятимерное гладкое многообразие, управление принимает значения на двумерной плоскости (u1,u2) Е R2, а гладкие векторные поля Х1, Х2 удовлетворяют условию полного ранга [1] на многообразии Q (система (1) вполне управляема, то есть для любых состояний q0, q1 Е Q существует траектория системы (1), удовлетворяющая условиям (2)). В настоящее время не существует методов явного решения задачи (1), (2) в общем случае. Удовлетворительное решение имеется лишь для некоторых специальных классов систем. Тем не менее такие задачи возникают в инженерии, где достаточно приближенного решения, погрешность ко- торого не превышает наперед заданной. В работе предлагается метод конструирования управлений (u1(t), u2(t)), переводящих систему (1) за время T > 0 из начального состояния q0 в терминальное состояние q1 с любой наперед заданной точностью е > 0, то есть в такое состо яние q1, что p(q1,q1') < е, где р — расстояние на многообразии Q.

У E 5=1 ⁽q 1 ^- 51) 2 .

Например, если Q — область в R 5 , то р =

Системы вида (1) характеризуются тем, что размерность про- странства управлений меньше размерности пространства состояний: 2 = dim R2 < dim Q = 5, однако любые точки пространства состояний могут быть соединены траекторией системы. В теории управления такие системы называются вполне неголономными. Нелинейные системы (1), линейно зависящие от управлений, количество которых меньше, чем размерность пространства состояний, характеризуются тем, что возможность перемещения неодинакова по различным направлениям. Величина смещения в направлении полей Х1 и Х2 за малое время t есть O(t), в направлении коммутатора (см. раздел 2) Х3 = [Х1, Х2] есть O(t2), в направлении Х4 = [Х1, Х3] и Х5 = [Х2, Х3] есть O(t3). В силу этой анизотропии пространства состояний, задача управления для таких систем весьма нетривиальна.

Конструктивная задача управления активно изучается в последнее время в нелинейной теории управления. Эта задача имеет удовлетворительное решение в случае систем, находящихся в цепной форме, и приводимых к такой форме обратной связью [2, 3], а также для дифференциально плоских систем [4]. Однако системы общего положения с двумя управлениями имеют вектор роста (2, 3, 5) (см. раздел 2), потому эти результаты неприменимы к таким системам.

В данной работе представлен способ отыскания приближенного решения задачи (1) , (2) , основанный на построении нильпотентной аппроксимации. Идея метода заключается в том, что исходная система приближается нелинейной системой более простой структуры, для которой точно решается задача управления. Затем найденные управления подставляются в исходную систему. Если состояние, достигнутое после применения найденного управления, отличается от желаемого состояния в пределах допустимой погрешности, то задача считается решенной, иначе процедура повторяется с новыми граничными условиями. Точное решение задачи управления нильпотентной системой дает приближенное решение исходной задачи управления в малой окрестности целевой точки. Метод нильпотентной аппроксимации применим к задачам управления общего вида; существенно только уметь решать задачу управления для нильпотентной аппроксимации. Этот метод предложен в работах [5 –9] .

В данной работе рассматривается задача управления нелинейными пятимерными системами общего вида, линейно зависящими от двумерного управления. Конкретными примерами систем такого вида, которые представляют самостоятельный интерес из-за своего прикладного значения в робототехнике, являются система, моделирующая качение без прокручиваний и проскальзываний шара по плоскости, и система, моделирующая движение машины с двумя прицепами по плоскости (см. раздел 3) .

• 2.    Математические определения

В этом разделе описаны используемые в статье математические понятия. Основным математическим аппаратом, применяемым для решения задачи управления (1) , (2) , является геометрическая теория управления [1] и субриманова геометрия [10] .

Траекторией системы (1) , выходящей из точки q° Е Q под действием управления (u 1 (t), u ₂ (t)), t Е [0,Т], будем называть кривую 7(t):[0,T] ^ Q, являющуюся решением задачи Коши

7(t) = X i (?y(t))u i (t) + X 2 (?y(t))u 2 (t), ?7(0) = q°, t Е [0,T].

Управления U j (t) являются кусочно-непрерывными функциями. Точка q = T](t o ) е Q для фиксированного t g е [0, Т ] называется достижимой из q ⁰ за время t ₀ . Множеством достижимости из точки q ⁰ за произвольное время t е [0, то ) называется множество

A q O = {q е Q | q достижима из q ⁰ за некоторое время t >  0 } .

Линейное пространство L называется алгеброй Ли, если на нем определена линейная по каждому аргументу, кососимметричная и удовлетворяющая тождеству Якоби бинарная операция (скобка Ли) [а,Ь], а,Ь е L. Пространство всех гладких векторных полей Vec(Q) образует бесконечномерную алгебру Ли, где в качестве скобки Ли выступает коммутатор векторных полей, который в координатах имеет выражение:

[А,В] =   А oq

fB, oq

А, В е Vec(Q).

Наименьшая подалгебра Ли в Vec(Q), содержащая векторные поля Х ^ , называется алгеброй Ли, порожденной полями Х ₁ ,Х ₂ , и обозначается Lie(X ₁ ,X 2 ).

Теорема Рашевского–Чжоу [1] утверждает, что любые две точки q ⁰ , q ¹ е Q достижимы друг из друга (dist(q ⁰ , q ¹ ) <  то ), если в любой точке q е Q линейная оболочка элементов алгебры Ли Lie(X ₁ ,X 2 ), порожденной полями X i , совпадает с касательным пространством T q Q (условие полного ранга). Предполагается, что система (1) удовлетворяет условию полного ранга, поэтому вполне управляема . Для вполне управляемых систем имеем V q ⁰ е Q A _q o = Q.

Определим субриманову длину траектории ^:

length(^) =

/Т

^ u 1 (t) + u 2 (t) dt.

Система (1) полного ранга индуцирует субриманово расстояние в Q, определяемое как

dist(q0, q1) = inf length(^), где инфинум берется по всем траекториям ^, соединяющим q0 с q1.

Зафиксируем q е Q и обозначим через L ^s (q) векторное пространство, порождаемое значениями в точке q скобок Ли полей X 1 , X 2 длины <  8,8 = 1,2,. .. (сами поля Х ^ — скобки длины 1):

L 1 (q) = span(X i (q),X 2 (q)),

L 2 (q) = span(L 1 (5) + [X i ,X 2 ](q)),

...

L ^s (q) = span(L ^s-1 (q)+

+ { [X _{i a} ,[X _{i s}-_t ,... X,4 ]...]](q) ln,...,i _s е { 1,2 }} ).

Условие полного ранга гарантирует, что для любой точки q е Q существует наименьшее целое число г = r(q) такое, что dim L ^r (q) = 5.

Обозначим n _s (q) = dimL ^s (q), 8 = 1, .. ., г. Вектором роста системы (1) в точке q называется вектор

⁽^ i ^(q), .. .,n _r ⁽q)).

Точка 5 называется регулярной, если вектор роста постоянен в окрестности точки q, иначе q называется сингулярной. В статье рассматриваются системы (1) в окрестности регулярных точек. Заметим, что для системы (1) общего положения точка общего положения будет регулярной, то есть вектор роста будет равен (2, 3, 5).

Управляемая система (1) называется нильпотентной , если соответствующая алгебра Ли Lie(X 1 ,X 2 ) нильпотентна, то есть для некоторого N е N

X,[X , 2 ,...,[X _{4 N} ,X , „ +1 ]...]] = 0,   ^...^n +1 е { 1,2 } .

• 3.    Неголономные системы в робототехнике

3.1.    Качение сферы по плоскости

Неголономными системами называются механические системы, стесненные неинтегрируемыми связями, которые налагаются на скорости точек системы, но не на положение системы. С точки зрения теории управления, управляемая система называется неголономной, если размерность множества достижимости A системы из произвольного состояния системы превосходит размерность множества скоростей В в этой точке (dim A > dim В). Система называется вполне неголономной, если размерность пространства состояний Q совпадает c размерностью множества достижимости A, но больше размерности множества скоростей В (dimQ = dim A > dim В). Система называется голономной, если dim В = dim A. Для управляемых систем (1), линейных по управлению, эти свойства выражаются в терминах алгебры Ли, порожденной исходными полями управляемой системы. Управляемая система голономна, если размерность пространства, порожденного алгеброй Ли, совпадает с размерностью пространства допустимых скоростей: Lie(X1, X2)(q') = span(X1, X2)(q'), Mq e Q (т.е. существует интегральное многообразие поля скоростей системы). Если же размерность пространства, порожденного алгеброй Ли, больше размерности пространства скоростей, то система неголономна.

В рассматриваемых системах (1) размерность управления меньше размерности состояния 2 = dim R ² < dimQ = 5, однако любые точки пространства состояний могут быть соединены траекторией системы (в предположении условия полного ранга). Это означает, что поставленная задача (1) , (2) является задачей управления для вполне неголономных систем. Изучение различных теоретических вопросов неголономных систем представляет большой интерес и является предметом исследований многих ученых как в России, так и за рубежом [1, 6 , 10, 11] .

Неголономные связи возникают в системах при качении твердых тел по поверхности без скольжения. В связи с развитием робототехники все более актуальной становится задача управления неголоном-ными механическими системами, которые представляют собой базовые модели разнообразных колесных роботов. Необходимым условием функционирования таких роботов является возможность самостоятельного перемещения. Эта задача математически формализуется как задача управления системой, которая моделирует исходную физическую систему с наложенными на нее ограничениями. Отметим, что речь идет о синтезе управления. Используя сведения о своем текущем состоянии, робот вырабатывает стратегию движения и перемещается в желаемое состояние. Для решения таких задач не требуется знания точного аналитического решения задачи управления, а достаточно приближенного решения, найденного с заданной точностью, и на первый план выдвигаются такие критерии, как скорость вычислений и простота реализации найденного закона управления.

В данной работе рассматривается задача управления нелинейными пятимерными системами общего вида, линейно зависящими от двумерного управления. Конкретными примерами систем такого вида, которые представляют самостоятельный интерес из–за своего прикладного значения в робототехнике, является система, моделирующая качение шара по плоскости без прокручивания и проскальзывания, и система, моделирующая движение машины с двумя прицепами по плоскости. Качение шара по плоскости аппроксимирует вращение предмета в руке робота в случае, когда рука робота плоская. Исследование задачи управления машиной с прицепами стимулируется многочисленными прикладными задачами, возникающими в процессе жизнедеятельности человека. К ним можно отнести, например, задачу автоматизированной транспортировки грузов (аэропорты, вокзалы, гипермаркеты, склады), или работу в опасной среде, или в среде с заранее неизвестными свойствами (доставка в опасную зону для выполнения различных операций, связанных с риском для жизни человека).

Для решения задачи управления такими системами был применен геометрический подход. Состояние системы задается как точка пятимерного пространства. На нем заданы два гладких векторных поля. Система непосредственно может перемещаться только в направлении любой линейной комбинации этих полей. Таким образом, размерность множества скоростей системы равна двум. Рассматриваются вполне управляемые системы, поэтому размерность множества достижимости совпадает с размерностью пространства состояний и равна пяти. Система может перемещаться в направлении коммутаторов исходных векторных полей, совершая при этом значительный маневр. Этот факт иллюстрирует свойство неголономности рассматриваемых систем.

Конкретным примером систем вида (1) является система, моделирующая качение сферы по плоскости без прокручиваний и проскальзываний. Задача о качении сферы по плоскости имеет большое значение для робототехники при моделировании движения шара в руке робота-манипулятора, а также в задаче управления сферическими роботами [12] . Качение сферы по плоскости является первым приближением при исследовании задач о качении произвольных поверхностей. Они вызывают большой интерес в механике, робототехнике и теории управления [1, 2 , 10, 11] .

Состояние системы «Сфера на плоскости» описывается точкой контакта сферы с плоскостью и ориентацией сферы в трехмерном пространстве. Требуется перекатить сферу из заданного начального состояния в заданное терминальное состояние. Управлением является скорость центра сферы. Обозначим через (ж, у) Е R2 точку контак-

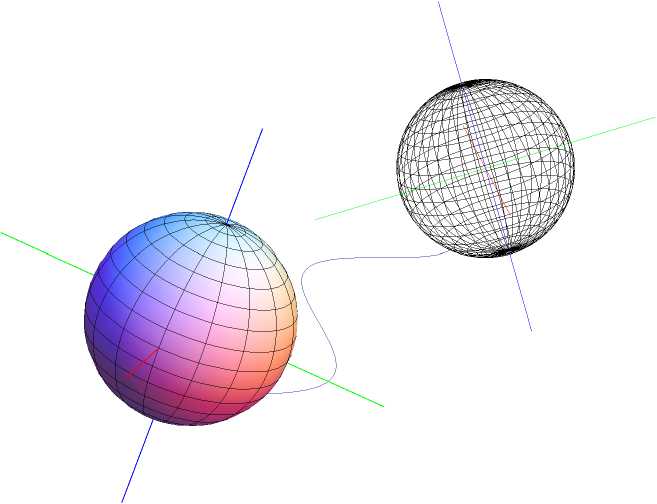
Рис. 1. Задача о качении сферы по плоскости

та сферы с плоскостью, а через q = (q ₀ ,q 1 ,q ₂ ,q ₃ ) Е S 3 — кватернион единичной длины, задающий ориентацию сферы в пространстве. Тогда управляемая система имеет вид (см. [13] ):

⎧ ж = Mi,     у = П2 , qo = 2(q2mi - qiм2),

• < qi = 2(q3Mi + qoм2), ^q2 = 2 ^(-qo^Mi + q3 ^M2), ^3 = 2(-qiMi — q2м2).

3.2.    Управление машиной с двумя прицепами

Пространство состояний Q = R ² x S 3 является пятимерным гладким многообразием, а векторные поля Х 1 = 2 (1, 0, q ₂ , q ₃ , — q ₀ , -q 1 ) ^т и Х ₂ = 2 (0,1, —q 1 , q ₀ ,q ₃ , — q ₂ ) ^т удовлетворяют условию полного ранга на Q.

Другим важным с точки зрения приложений примером системы вида (1) является система, моделирующая движение по плоскости машины с двумя прицепами. Состояние системы определяется пятью координатами £ = (х,у,6,ф 1 ,ф 2 ). Здесь х,у — координаты центра машины на плоскости, 6 — угол, задающий ориентацию машины на плоскости, ф 1 — угол, который задает положение первого прицепа относительно машины, ф ₂ задает положение второго прицепа относительно первого прицепа (см. Рис. 2) . Управлением (u 1 ,u ₂ ) является линейная скорость.

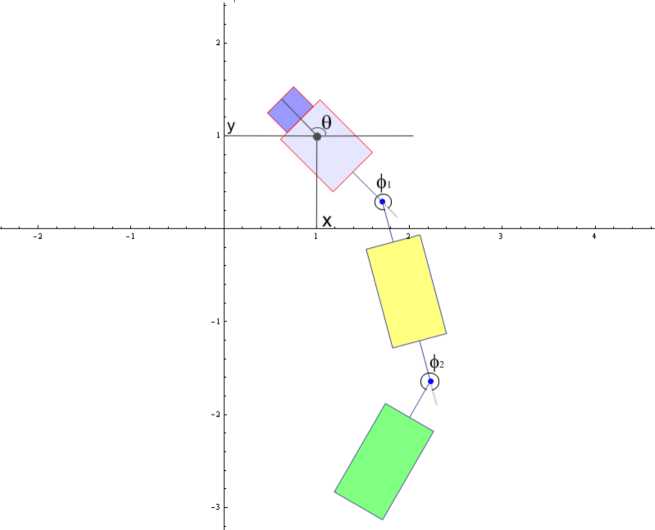
Рис. 2. Машина с двумя прицепами

Динамика системы имеет вид (см. [2] ):

i = cos 9и1, у = sin 9и1,

A

< 9 = U2, ф1 = — sin ф1и1 — (1 +cos ф1)и2,

^2 = (sin(ф 1 — Ф 2 ) + sin ф 1 )и 1 + (cos(ф 1 — Ф 2 ) +cos ф 1 )и 2 .

Это — система вида (1) , где поля Х 1 и Х ₂ имеют вид:

Х 1 = (cos 9, sin 9, 0, — sin ф 1 , sin(ф ₁ — ф ₂ ) + sin ф 1)^т , Х ₂ = (0, 0,1, — 1 — cos ф 1 , cos(ф ₁ — ф ₂ ) + cos ф 1 ) ^т .

Заметим, что система (6) не управляема, если ф 1 = тт или ф ₂ = тт. В дальнейшем будем рассматривать пространство состояний системы R ² х S ¹ х (S ¹ \ { т } ) ² . Вычислив коммутаторы

Хз = [Х1,Х2], Х4 = [Х1,Хз], Х5 = [Х2,Хз], можно проверить, что векторные поля Х^, г = 1,..., 5, линейно независимы всюду, кроме особых поверхностей ф1 = ф2. Точки этих поверхностей являются сингулярными. Мы будем рассматривать систему вдали от этих особых поверхностей.

Анимация на рис. 2 вставлена с использованием пакета PDFAnim (см. .

• 4.    Алгоритм поиска приближенного решения задачи (1), (2)

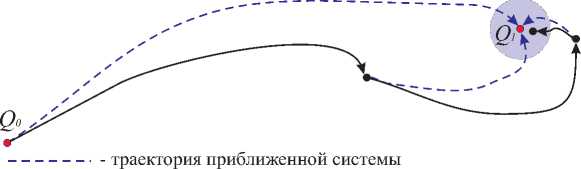
Итерационный алгоритм приближенного решения задачи (1) , (2) основан на локальном приближении исходной нелинейной системы приближенной нильпотентной системой (см. пункт 4.1) , для которой задача управления решается точно на каждой итерации. Итак, имеется исходная система в начальном состоянии q ⁰ , требуется найти управление, переводящее систему в целевое состояние q ¹ с наперед заданной точностью е > 0. Поиск приближенного решения осуществляется следующим образом:

• (1)    в окрестности целевой точки строится аппроксимирующая система;

• (2)    точно решается задача управления для приближенной системы;

--траектория исходной системы

Рис. 3. Итерационный алгоритм поиска приближенного управления

• (3)    найденные управления подставляются в исходную систему, и если достигнутое состояние не попадает в е-окрестность целевого состояния, то нужная точность не достигнута, и шаг (2) повторяется с новым граничным условием — в качестве начального состояния выбирается состояние, достигнутое на предыдущей итерации алгоритма, иначе вычисления прекращаются.

4.1.    Нильпотентная аппроксимация

Локальное приближение управляемой системы другой, более простой системой, широко используется в теории управления. Обычно в качестве локальной аппроксимации используется линеаризация управляемой системы. Однако для линейных по управлению систем вида (1) линеаризация дает слишком грубое приближение. Так как размерность управления меньше размерности состояния, то линеаризация не может быть вполне управляемой. Естественную замену линейной аппроксимации в этом случае доставляет нильпотентная аппроксимация — наиболее простая система, сохраняющая структуру управляемости исходной системы (в частности, сохраняется такой важный инвариант как вектор роста).

Понятие нильпотентной аппроксимации управляемых систем введено независимо А. А. Аграчевым и А. В. Сарычевым [5] , и Х. Хермсом [7] . В работе используется алгоритм вычисления нильпотентной аппроксимации, предложенный А. Беллаишем [6] , конкретизированный для систем (1) и дополненный переходом в систему координат, в которой нильпотентная аппроксимация имеет канонический вид (7) .

Рассмотрим алгоритм построения нильпотентной аппроксимации для систем (1) в окрестности состояния q ¹ :

• (1)    Вычисление коммутаторов

Х 3 = [Х 1 ,Х 2 ], Х 4 = [Х 1 ,Х з ], Х 5 = [Х 2 ,Х з ].

Веса полей Х 1 , Х ₂ , Х ₃ , Х 4 , Х 5 соответственно равны (1,1, 2, 3, 3).

• (2)    Используя исходные координаты q, вычисляются координаты у следующим образом:

У = a(q) = Г(-1)(q - q1), где Г — это матрица размерности 5x5, составленная из элементов Гу, определяемых по формуле:

⁵ Х■ ^{g Г}« ^ ,

При такой замене точка q ¹ переходит в начало координат.

• (3)    Выполняется переход

А : у ^ х в привилегированные координаты х с помощью замены:

X;      у;, t 1, . . . , 3, х4 = У4 - |(У2О1 + 2У1У2О2 + У2 Оз), х5 = У5 - |(У2О4 + 2У1У2О5 + У2О6), где

^О 1 = ^Х 1 ^(Х 1 l^X q ¹ ), ^О 2 = ^Х 1 ^(Х 2 ⁽У 4 ⁾⁾⁽q ^{1 ), О} 3 = ^Х 2 ^(Х 2 ⁽У 4 ⁾⁾⁽q ^{1 ),} 0 4 = Х 1 (Х 1 (у 5 ))(q ¹ ), 0 5 = Х 1 (Х 2 (у 5 ))(q ¹ ), О б = Х 2 (Х 2 (у 6 ))(q ¹ ).

Здесь Х _; (/) = (V /, Х _; ) обозначает производную функции / по направлению векторного поля Х _; (оператор ( , ) обозначает скалярное произведение, а V — взятие градиента).

• (4)    Используя разложение векторных полей Х _; (х) в ряд Маклорена, строится нильпотентная аппроксимация в координатах х:

;х = ^Х1(х)«1 +Х2(х)и2, х е R5, (u1,u2) е R2, где

^х (=) = ^Xj(o) A ₊^х2«» ; ₊

(S

dX ³ (z) Э? _г

? ) Й⁺

/ ал>) д? з

? 3

, d 2 (X 4 (z))

⁺   д? ²

? 2 +

2 = 0

д ² (X 4 (z))

⁺    8? 2

2 d ² (X 4 (?))

^{2 +} д? 1 д? 2

д

? 1 ? 2       +

/ д? 4

/ дх 5 (?) д? з

д ² (х 5 (?))

⁺   д? 2

? 1 ² +

2 = 0

₊ д ² (X 5 (?))       2 ₊ ■ ■ ■<         ,,) "

dz ²      2 =0 ^{2 d}? 1 ^d? 2 2 =0 ¹ 2) ^d? 5 ’

J = 1, 2.

• (5)    Вычисляется замена переменных Ф для перехода в систему координат, в которых нильпотентная аппроксимация имеет канонический вид:

У 1 = ^М 1 ,

У 2 = М 2 ,

у Е R ⁵ .

' У3 = 2 ⁽У 1 ^М 2 ^- У 2 ^М 1 ⁾, У 4 = 2 ⁽У 2 ⁺ У ^{2 )}М 2 , /У5 = ^- 2 ⁽У 1 ⁺ У 2 ^)м 1 ,

Известно [14] , что любые две пятимерные нильпотентные системы с вектором роста (2, 3, 5) диффеоморфны. Замена переменных, переводящая одну такую систему в другую, строится следующим образом. Пусть X 1 , X 2 — векторные поля первой, а Y 1 , Y 2 — векторные поля второй нильпотентной системы с вектором роста (2, 3, 5). Вычислив коммутаторы X 3 , X 4 , X 5 и Y 3 , Y 4 , Y 5 , можно построить диффеоморфизм, переводящий поля Х ^ в окрестности точки $ 0 в поля Y^ в окрестности У 0 :

Ф: 0(^ 0 ) ^ О(у 0 ),  Ф * (Х _г ) = Y , .

Определим отображения F и G как композицию потоков векторных полей Х _г и У соответственно за время t _i :

F (t i , .. ., t 5 ) = e^{t5 X} 5 о • • • о e^{t1 X} 1 (х о ),

G(t i ,... /( 5 ) = e^t5Y 5 о • • • о e ^{t 1 Y} 1 (у о ).

Тогда искомый диффеоморфизм имеет вид

Ф = G о F - 1 .

Итак, предложен способ задания диффеоморфизма, переводящего поля Х _г исходной системы (1) из окрестности точки q ¹ в поля системы У в окрестности начала координат, нильпотентная аппроксимация которой имеет канонический вид (7) :

т = Ф о А о а.

4.2.    Кусочно-постоянные управления

Рассмотрим задачу управления нильпотентной канонической системой (7) с граничными условиями

• (8)                     у(0) = У 0 ,      у(1) = (0,0,0,0,0).

Требуется найти управления u 1 (t) и u ₂ (t) на отрезке [0,1] в классе кусочно-постоянных функций такие, что для произвольной точки у ⁰ е R ⁵ соответствующая траектория удовлетворяет условиям: у(0)= у ⁰ , у(1) = (0,0,0, 0, 0).

С использованием системы Wolfram Mathematica было показано, что для решения задачи управления (7) , (8) достаточно управлений с тремя точками переключения:

а _г , при t е [0, 4 ],

К г

Зг, при t е (4, 2], 7г, при t е (2, 4], ,5г, при t е (4, 1], где г = 1, 2.

Последовательное интегрирование системы (7) дает выражение для конечной точки, в которую переходит система после примененных управлений кг. Получается система из пяти алгебраических уравнений относительно уо и коэффициентов управления. Вначале показывается, что управлений с двумя переключениями кг = {аг,Ьг,сг} недостаточно для решения задачи (7), (8). Для этого требуется проверить, что получившаяся система уравнений неразрешима относительно коэффициентов управления при произвольном у0. Заметим, что система состоит из пяти уравнений с шестью неизвестными {й. , bi, с-}, и возникает свобода выбора, относительно каких из неизвестных решать систему. Однако никакой выбор не дает решения при произвольном у0. Далее показывается, что управлений с тремя точками переключения достаточно для разрешимости получившейся системы при любом у0 Е R5.

Требуется найти коэффициенты управления a _t , P . , 7 . , 5 _t . Для этого решается система из пяти алгебраических уравнений с восемью неизвестными:

У 1 (а - , ... ,5 . ) = 0,

У 2 (а . , . ..,5 .) = 0,

' У з (« - ,...Л ) = 0,

У 4 (а - , ...,5 . ) = 0,

_У5 (а - ,..., 5 - ) = 0.

Получается трехпараметрическое семейство решений. Формулы имеют сложный вид, поэтому в статье не приводятся. Для любого начального состояния у ⁰ существует способ зафиксировать свободные параметры так, чтобы получалось решение без особенностей. Кроме того, желательно получить управления такие, чтобы длина соответствующей траектории (в некоторой естественной метрике) была как можно меньше. В зависимости от того, какие коэффициенты выбираются в качестве свободных параметров, получаются различные формулы для оставшихся коэффициентов управления. В качестве свободных параметров предлагается выбирать 7 1 , 5 1 , 5 2 или 7 2 ,5 1 , 5 2 . Остальные коэффициенты управления выражаются через свободные параметры. Введем показатель Amp = max( | a _t | , IP . | , | 7 - | , | 5 - | ), характеризующий величину отклонения искомой траектории от постоянной траектории. Свободные параметры предлагается фиксировать в соответствии с критерием Amp ^ min.

4.3.    Оптимальные управления

Рассматривается задача оптимального управления системой (7) с граничными условиями

• (9)                   у(0)= у ⁰ ,       у(Т ) = (0,0, 0, 0,0),

с естественным интегральным критерием (минимальность функционала субримановой длины)

/^т

^u 1 (t) + м 2 (t)dt ^ min .

Эта задача известна в теории управления как обобщенная задача Дидоны [15] , а в субримановой геометрии как нильпотентная субриманова задача с вектором роста (2,3,5). Она имеет богатую историю и была детально теоретически изучена Ю. Л. Сачковым [15 –18] . Основным результатом теоретических исследований явилось описание структуры экспоненциального отображения и первых времен Максвелла вдоль экстремальных траекторий. На основе этого задача оптимального управления (7) , (9) , (10) была сведена к задаче решения пяти алгебраических уравнений в неэлементарных функциях с пятью неизвестными. Явно решить эту систему практически не представляется возможным ввиду сложности получившихся формул, поэтому было решено использовать численные методы.

Приведем некоторые результаты из статей [15 –18] , необходимые для дальнейшего изложения:

• (1)    Семейство экстремальных траекторий параметризуется экспоненциальным отображением Exp, переводящим пару (вектор сопряженных переменных, время) в соответствующую точку экстремальной траектории. Задача построения оптимального синтеза состоит в обращении экспоненциального отображения.

• (2)    Прообраз L и образ М экспоненциального отображения разбиваются поверхностями разреза на 4 области (L = U 4= ₁ L _i в прообразе и М = и ⁴ = ₁ М _г в образе) таких, что L _г переходит в М _г и экспоненциальное отображение является диффеоморфизмом на этих областях.

• (3)    Каждая область L _г разбивается на два непересекающихся множества С ₁ и С 2 , в которых экспоненциальное отображение задается разными формулами.

• (4)    Разбиение L на L _г и М на М _г известно, а разбиение на C j неизвестно.

• (5)    В задаче (7) , (9) , (10) имеется двумерная группа симметрий, состоящая из вращений и растяжений. Факторизация задачи по

этой группе уменьшает размерность задачи с пяти до трех. Получается система из трех уравнений с тремя неизвестными:

Г Р (u,v,k) = Р 1 ,

• ⁽¹¹⁾                         < Q(u, v,k) = Q i ,

I R(u, v, к) = R 1 .

Итак, для построения оптимального синтеза в задаче (7) , (9) , (10) требуется решить систему (11) относительно (u, v, к) при заданной правой части Р 1 , Q 1 , R 1 . Известно, что при произвольной правой части (за исключением особых множеств меньшей размерности) система (11) имеет единственный корень. Заметим, что функции Р(u, v, к) Q(u,v,k) и R(u,v,k) выражены в эллиптических интегралах первого и второго рода. Кроме того, они имеют сложную аналитическую запись (занимают несколько страниц текста). В приложении в конце статьи приведены формулы для случая С 1 .

Предлагается следующий генетический алгоритм решения системы (11) (см. Рис. 5 и Рис. 4) :

• (1)    Определение области L , по правой части P 1 ,Q 1 ,R 1 .

• (2)    Поочередный выбор С 1 , С 2 (или одновременное выполнение на 2-х процессорах).

• (3)    Создание начальной популяции п случайных приближений (особей популяции) для корня.

• (4)    Сортировка популяции по приспособленности. Особь обладает тем лучшей приспособленностью, чем меньше невязка

• (12)              // Р(u, v, к}² + Q(u, v, к}² + R(u, v, к) ² .

• (5)    Эволюция. Над особями популяции определены две операции: «мутация особи» (метод Ньютона решения системы уравнений) и скрещивание особей (метод хорд решения системы уравнений). Кроме того, к популяции добавляются случайные особи, во избежание сходимости алгоритма к ложному корню (точка локального минимума невязки (12) , не являющаяся корнем системы (11) ).

• (6)    Отбор п наиболее приспособленных особей. Если невязка лидера популяции меньше заданного значения е, то корень найден. Иначе переход к пункту (5).

• 5.    Программный комплекс MotionPlanning

Выбор такой схемы поиска корня был обусловлен особенностями решаемой системы. Было обнаружено, что невязка (12) имеет много локальных минимумов. В связи с этим, сходимость стандартного метода

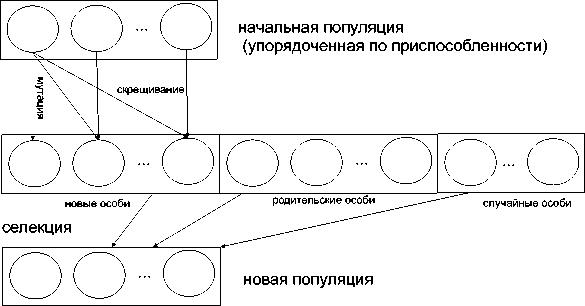
Рис. 4. Генетический алгоритм решения системы алгебраических уравнений

Ньютона сильно зависит от того, насколько удачно выбрано начальное приближение. Кроме того, были замечены случаи, когда в малой окрестности корня невязка терпит сильные изменения: внутри области значение невязки мало, а вне этой области значение невязки велико. При этом и внутри, и вне этой области имеются несколько локальных минимумов. В этом случае вероятность удачного выбора начального приближения для метода Ньютона становится крайне мала. Введение популяции начальных приближений позволяет оставаться в описанной окрестности корня (один раз попав в нее) даже если метод Ньютона (мутация) не сошелся к корню. Метод хорд (скрещивание) исследует окрестность найденного лучшего приближения (лидера популяции), помогая выбраться из точки локального минимума.

В среде Mathematica 8 был разработан программный комплекс MotionPlanning (см. Рис. 5) решения задачи (1), (2). Он является дополнительным пакетом для системы Wolfram Mathematica (MotionPlanning.m) и состоит из следующих функциональных модулей:

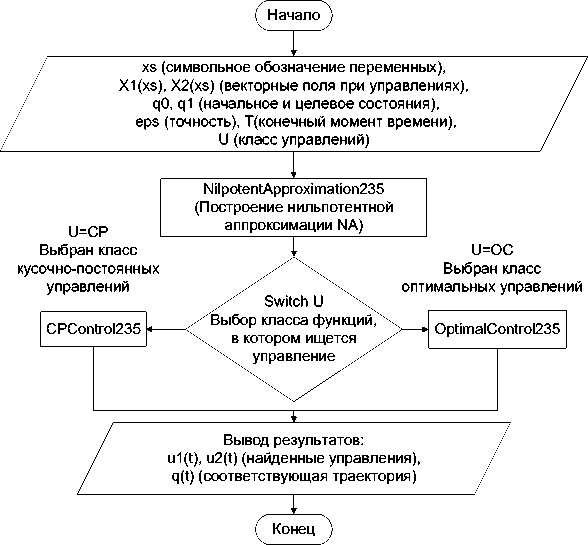
Рис. 5. Структура ПК MotionPlanning

∙ NilpotentApproximation строит нильпотентную аппроксимацию NA (см. п. 4.1) системы (1) и возвращает замену переменных т = а о А о Ф, в которых NA имеет канонический вид (7) .

∙ CPControl решает задачу (1) , (2) в классе кусочно-постоянных управлений (см п. 4.2) .

∙ OptimalControl решает задачу (1), (2) в классе оптимальных для нильпотентной системы (7) управлений (см. п. 4.3). Пользователь может легко организовать параллельное вычисление корня на нескольких ядрах процессора. Для этого требуется указать системе Mathematica 8 (функция недоступна в более ранних версиях) количество ядер и изменить, при необходимости, функцию SolveHen (выбрать какие и сколько из алгоритмов решения системы АlgorithmA, АlgorithmB, АlgorithmC, АlgorithmD будут выполняться одновременно). Перечисленные алгоритмы являются q=q0

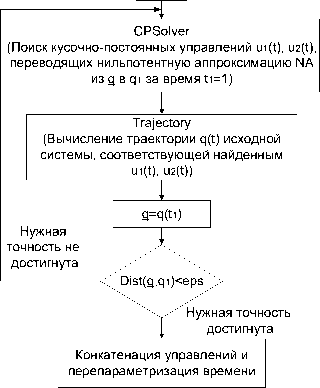
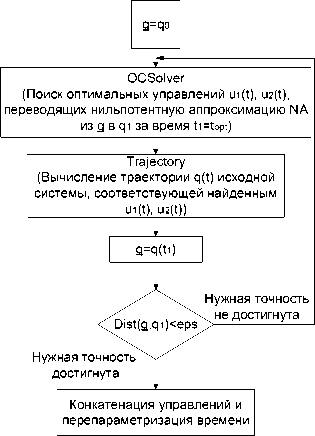
Рис. 6. Модуль CPControl и OptimalControl решения задачи (1) , (2) в классах кусочно-постоянных и оптимальных управлений

конкретными реализациями генетического алгоритма, описанного в п. 4.3 . Они различаются как по количеству особей популяции, так и по закону эволюции. Кроме стандартного метода Ньютона (АlgorithmA) и метода хорд (АlgorithmB), пользователю предлагаются гибридные методы (АlgorithmC, АlgorithmD). Проведенное обширное тестирование показало, что в большинстве случаев первым результат выдает АlgorithmA или АlgorithmB, хотя и встречаются ситуации, когда гибридные методы справляются с задачей быстрее. Поэтому по умолчанию предлагается делить доступные ядра пополам между AlgorithmA и АlgorithmB. Отметим, что одновременный запуск одного и того же алгоритма на разных ядрах имеет смысл, так как во всех алгоритмах используется генератор случайных начальных приближений. Так как основное время вычисления занимает выбор удачного начального приближения, то использование нескольких ядер дает существенное ускорение.

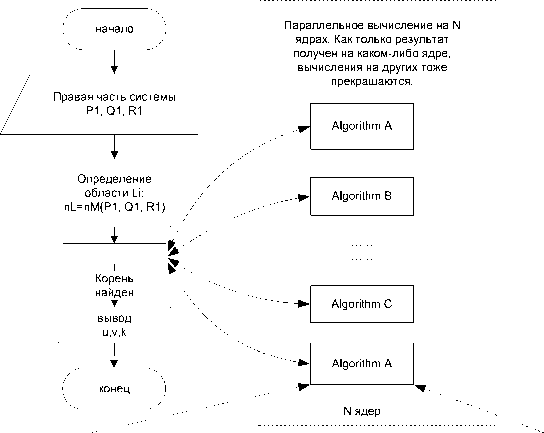
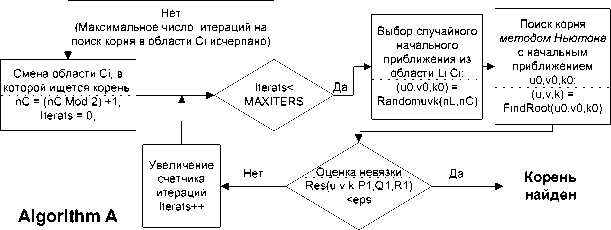
Рис. 7. Схема работы модуля OptimalControl

∙ Дополнительные функции ПК MotionPlanning.

Помимо основных модулей комплекса MotionPlanning, решающих задачу (1) , (2) (NilpotentApproximation, CPControl и OptimalControl), пользователю предоставляются некоторые дополнительные инструменты для представления результатов и слежения за процессом вычислений. Речь идет о следующих функциях:

• •    TrajectoryNatPar[X 1 , Х 2 , { u 1 ,u ₂ ,T } ,q ⁰ ,xs] возвращает q(t) траекторию системы (1) , где t e [0,Т], соответствующую управлениям {u 1 ,u ₂ }, выходящую из точки q°. На рис. 8 приведен пример использования функции TrajectoryNatPar для построения (ParametricPlot) проекций на плоскость семейства оптимальных траекторий в обобщенной задаче Дидоны (7) , (9) , (10) ;

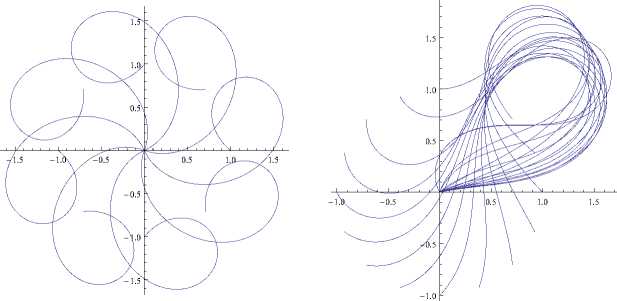
Рис. 8. Пример использования функции TrajectoryNatPar

• •    PlotTrajectoryNatPar[trajectory, q ⁰ , q ¹ , Т ] строит разным цветом графики пяти компонент заданной траектории trajectory (t) за время t e [0, Т], а также отмечает на графике заданные состояния q ⁰ и q ¹ . Эта функция может использоваться для визуальной оценки достигнутого состояния и найденных траекторий. Пользователь может включить режим работы ПК, в котором графики найденных траекторий будут выводиться на экран на каждой итерации. На рис. 9 приведен пример использования функции PlotTrajectoryNatPar;

• •    PlotTrajectoryOtklNatPar[trajectory, q ⁰ , q ¹ , Т ] строит разным цветом графики отклонений пяти компонент заданной траектории trajectory(t) за время t e [0, Т] от состояния q 1 ;

• •    AnimateCar[trajectory, Т, q ⁰ ,q 1 , N, {х _тгп , x _max ,y _mln ,y _max }] строит анимацию движения машины с двумя прицепами, при движении по траектории trajectory(t) за время t e [0, Т] из состояния q ⁰ . Область, по которой движется машина с прицепами, ограничивается прямоугольником {{X min ,X max }, {y min ,y max }}. В результате на жестком диске создается последовательность из

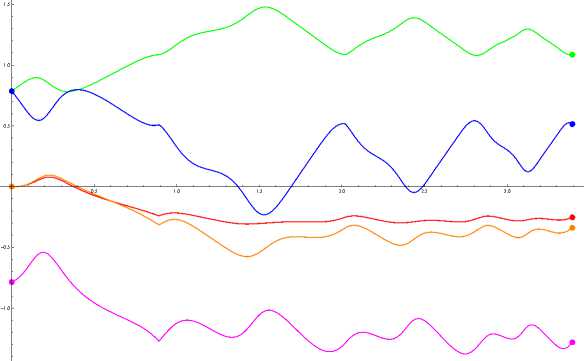
Рис. 9. Функция PlotTrajectoryNatPar построения компонент траектории

N кадров. Последовательность кадров — это упорядоченный набор изображений в формате PNG, который впоследствии легко может быть собран в видеофайл стандартными утилитами. Размер изображения является параметром, доступным пользователю (по умолчанию 1024*768 пикселей). Помимо положения машины и прицепов, на каждый кадр пунктиром наносится состояние q ¹ . Функция предназначена как для самостоятельного использования (моделирование системы «машина с двумя прицепами» и ее исследование), так и для проверки решений найденных с помощью ПК MotionPlanning (cм. рис. 2) .

• •    AnimateBall^rcyectory, Т, q ⁰ ,q 1 ,N] визуализирует качение сферы без прокручиваний и проскальзываний по заданной траектории (аналогично функции AnimateCar) (cм. рис. 1) .

• 6.    Пример использования ПК MotionPlanning

Приведенный алгоритм поиска приближенного управления (см. раздел 4) , основанный на построении нильпотентной аппроксимации, решает локальную задачу управления (т.е. когда начальное q ⁰ и конечное q ¹ состояния не слишком далеки). Алгоритм реализован в ПК MotionPlaning. В дальнейшем планируется расширить функции ПК для решения глобальной задачи управления (т.е. когда начальное q ⁰ и конечное q ¹ состояния далеки). Предполагается соединять q ⁰ и q ¹

непрерывной кривой, и разбивать ее промежуточными точками так, чтобы на каждом отрезке возникала локальная задача управления (см Рис. 10) .

Рис. 10. Решение глобальной задачи

Продемонстрируем работу комплекса на задаче о перемещении машины с двумя прицепами из начального состояния

'° = ( 0- 0,1,1, - J )

в целевое состояние q1 = (-0.252, -0.339, 1.085, 0.514, -1.281)

с точностью e = 10 ^-3 . На рис. 11 и рис. 12 приведены графики отклонения от целевого значения q ¹ найденной траектории, соответствующей найденному кусочно-постоянному и оптимальному управлению. В случае применения кусочно-постоянных управлений, алгоритму потребовалось 6 итераций для достижения требуемой точности, а для оптимальных управлений потребовалось 4 итерации. Заметим, что при использовании кусочно-постоянных управлений система совершила больший маневр (траектория имеет большую амплитуду отклонений от целевого состояния).

• 7.    Заключение

Рассматриваемый в работе метод приближенного решения двухточечной задачи управления (1) , (2) был реализован в параллельном программном комплексе MotionPlaning. Комплекс был испытан на двух прикладных задачах (задача о качении шара по плоскости и задача управления машиной с двумя прицепами). В случаях, когда граничные условия не были слишком далеки, комплекс успешно

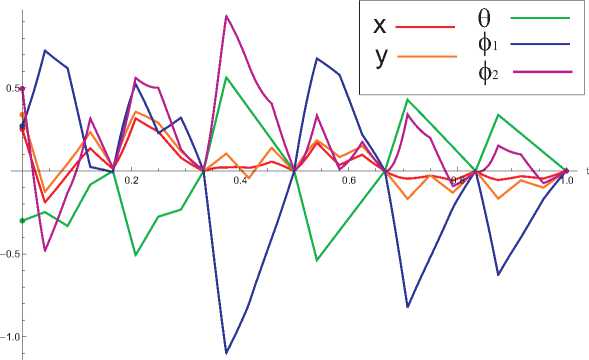
Рис. 11. График отклонения траектории, соответствующей кусочно-постоянному управлению

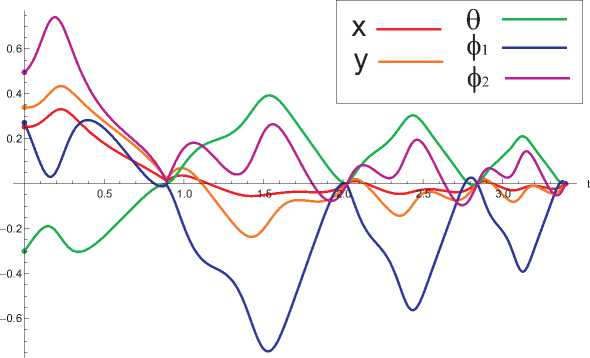
Рис. 12. График отклонения траектории, соответствующей оптимальному управлению решал поставленную задачу управления. В случаях далеких граничных условий алгоритм не сходился, что соответствует теоретическому обоснованию метода (нильпотентная аппроксимация является локальным приближением исходной системы). В будущем планируется расширить функционал ПК для решения глобальной задачи управления, путем ее сведения к последовательности локальных задач. В настоящее время ПК MotionPlaning является удобным и надежным средством решения локальной задачи (1), (2).