Алгоритмизация формирования и прагматической трансформации ограничений существования свойств предметной области

В инжиниринге онтологий сосуществуют два различных математически хорошо обоснованных подхода, основанных на теоретико-множественной семантике.

Наибольшее признание, распространение и значение (в том числе для развития теории и практики в ряде смежных областей) получил в этом смысле анализ формальных понятий (АФП) [1-3]. Более двух десятилетий он служит базой для развития и совершенствования методов построения, сравнения, объединения и т.д. формальных онтологий (см., например, ретроспективную подборку [4-10]). На наш взгляд, этот успех во многом определяется тем, что концепции и модели АФП оказались адекватны чрезвычайно востребованной ныне парадигме анализа данных , или, как теперь принято говорить, «науки о данных»\

Фундаментальная форма представления эмпирической информации в анализе данных - таблица «объекты-свойства» [11, 12] - фактически тождественна модели исходных данных АФП - многозначному формальному контексту

( G , M , V , I ) ,                                           (1)

где G = {gi}i = 1,_, r, r = |G| > 1 - множество объектов; M = {m,}, = 1,_, ,, 5 = |M| > 1 - множество признаков объектов («свойств»); V - совокупное множество значений разных свойств, V = и, = 1,_, V, Vj - область существования значений (домен) свойства m,; I - тернарное отношение между G, M и V (I с G х M х V), определённое для всех пар из G х M. Грануляция (1) с помощью концептуального шкалирования [13, 14] формирует2 ключевую структуру АФП -однозначный формальный контекст (G, M, I), где I - бинарное соответствие между G и M (Iс G х M), в котором рассматриваются операторы Галуа ф, ю (общая нотация «'») [1]: ■  фХ) = X' = {m, | m, е M, Vgi е X: I(gi, m,) = True} - общие свойства объектов, составляю щих X с G;

• ■   ю ( Y ) = Y ' = { g i | g i е G , V m , е Y : I ( g i , m , ) = True } - объекты, которые обладают всеми

свойствами из Y с M ;

• ■    для набора объектов X совокупность их общих признаков X ' служит описанием сходства этого набора объектов, а замкнутое множество X '' является кластером сходных объектов.

Анализ соответствия Галуа между булеанами 2 G и 2 ^M позволяет выявить бикластеры ( X , У ), X с G , Y с M , X = Y ', Y = X ', которые сохраняют информацию об объектах с одинаковым составом свойств и находятся по вложенности составов в отношении частичного порядка. Фундаментальная роль такого анализа (и в целом АФП) состоит в том, что названные его результаты соответствуют в философии и классической логике определению понятия и отношению обобщения на множестве понятий [15, 16]. Т.е. каждый выявленный бикластер ( X , Y ) описывает понятие (точнее - формальное понятие ), у которого X - объем , Y - содержание , и ( X 1 , Y 1 ) < ( X ₂, Y ₂), если Y 1 ^ Y ₂ (или, равно, X 1 с X ₂). Если интерпретировать (1) как данные многомерных наблюдений и измерений в исследуемой и моделируемой ПрО [4], то совокупность выявленных формальных понятий и связывающее их бинарное отношение частичного порядка «<» (« is a ») определяет, по меньшей мере, «скелет» формальной онтологии этой ПрО.

Принципиально иной подход в инжиниринге онтологий предлагают авторы [17-19]. В его основе лежит концепция ограничений существования свойств (ОСС) - исходная данность трёх бинарных отношений на множестве принимаемых во внимание свойств объектов ПрО:

• ■    обусловленность C : MхM ^ { True , False }, которая устанавливает, что всякий объект g обладая свойством m , обладает и свойством m k (хотя обратное может быть неверно), т.е.

во введённых обозначениях С ( m , , m k ) ^ V g е G : m , е { g }' ^ m k е { g }'. Обусловленность рефлексивна, несимметрична и транзитивна (рисунок 1a);

• ■    взаимообусловленность Н : M х M >  { True , False } - рефлексивное, симметричное и транзитивное отношение, индуцируемое отношением обусловленности:   H ( m , , m k ) о

С ( m , , m k ) л С ( m k , m , ) (рисунок 1б);

• ■    несовместимость E : M х M >  { True , False }, когда всякий объект g, обладая свойством m , , не может иметь m k в качестве другого свойства, и наоборот, т.е. E ( m , , m k ) о V g е G : m , е { g }' ^ m k t { g }'. Отношение E антирефлексивно, симметрично и нетранзитивно, но характеризуется так называемой «транзитивностью относительно обусловленности» (« EC -транзитивностью»), что означает V x , y , z е M : С ( x , у ) л E ( у , z ) ^ E ( x , z ) (рисунок 1в).

Q - свойство; „.-об- обусловленность;  ^— несовместимость;

Рисунок 1 - Примеры ограничений существования свойств (самообусловленность свойств не изображена)

Тогда формирование онтологии ПрО из набора характеризующих её свойств (т.е. свойств объектов ПрО) и набора ограничений существования (т.е. ОСС как набора сопряжённых пар свойств , реализующих экзистенциональные отношения обусловленности и несовместимости свойств) состоит в выявлении всех нормальных подмножеств актуальных свойств ПрО, которые замкнуты и совместимы :

• ■    Y с M замкнуто, если оно содержит все свойства, обусловленные любым элементом Y , т.е. V m , е Y : ( 3 m k е M , m k * m , : С ( m , , m k )) ^ m k е Y ;

• ■    Y с M совместимо, если любые два элемента Y не связаны отношением несовместимости, т.е. V m , е Y : ( 3 m k е M , m k * m , : Е ( m , , m k )) ^ m k t Y .

Нормальные подмножества актуальных свойств ПрО описывают все формальные понятия искомой онтологии, которые по вложенности составов нормальных множеств свойств организуются в граф наследования « is a ».

В контексте вышесказанного наш вклад состоит в развитии онтологического анализа данных (ОАД) - комплекса моделей и методов вывода формальных онтологий ПрО из характеризующих её неполных и противоречивых эмпирических данных, представленных в форме обобщённой таблицы «объекты-свойства» [20, 21]. При этом установлена общность очерченных формальных подходов в аспекте единства их гипотетико-дедуктивной основы и необходимость их совместного использования в ОАД [22, 23]. Последнее объясняет интерес к формированию наборов измеряемых свойств ПрО и ОСС как в аспекте их генезиса и когнитивных задач - эти вопросы рассмотрены в [22, 23], - так и чисто в структурном плане, что является предметом этой работы.

В предлагаемой статье решается задача алгоритмизации пошагового формирования и модификации субъектом ОАД набора свойств с ОСС, а также его преобразования в набор частично пересекающихся групп сопряжённых свойств, обеспечивающих эффективную идентификацию нормальных множеств свойств ПрО. В отличие от техники нормализации, основанной на булевых функциях и уравнениях, которая предложена в [17, 18], используется «естественное» описание ОСС в форме графов (см. рисунок 1) и матриц инцидентности. Это по нашему убеждению предопределяет б ольший когнитивный и «объясняющий» потенциал такого представления для субъекта ОАД, а также эффективную машинную реализацию соответствующих алгоритмов. Кроме того, алгоритмы модификации реализуют не имеющие аналогов методы расширения набора актуальных свойств с ОСС, которые опираются непосредственно на фундаментальные законы классической логики [22, 23].

1 Пошаговое формирование набора свойств с ограничениями существования

Для обозначения свойств объектов исследуемой ПрО, или измеряемых свойств , в данном разделе используются идентификаторы, у которых первым символом является строчная латинская буква, например, x е M.

Здесь и далее до определённого момента не принимается во внимание (в силу локальности действия) имманентная самообусловленность каждого свойства. Тогда нетрудно видеть, что с каждым свойством в наборе свойств с ОСС связаны три множества (рисунок 2):

• ■   C ( x ) — множество свойств, обусловливающих свойство x , 0 <  | C ( x ) | <  | M - 1,

• ■    C ( x ) - множество свойств, обусловленных свойством x , 0 <  | C ( x ) | <  | М | - 1,

• ■    Е ( x ) - множество свойств, несовместимых со свойством x , 0 <  | Е ( x ) | <  | М | - 1,

• -    причём лишь C ( x ) и C ( x ) могут пересекаться. Очевидно несложное выявление C ( x ), C ( x ) и Е ( x ) будем относить к числу базовых алгоритмических примитивов , которые не детализируются.

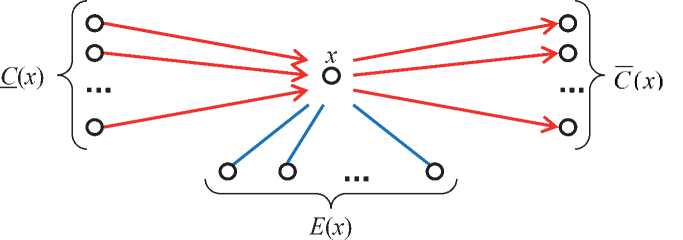
Рисунок 2 - Множества свойств, ассоциированные в наборе свойств с ограничениями существования с каждым отдельно взятым свойством (пояснение графических образов см. на рисунке 1)

В разделе рассматриваются два следующих элементарных созидательных действия:

• 1)    добавление нового свойства в существующий набор измеряемых свойств;

• 2)    добавление новой сопряжённости пары свойств - обусловленности или несовместимости - в набор ОСС.

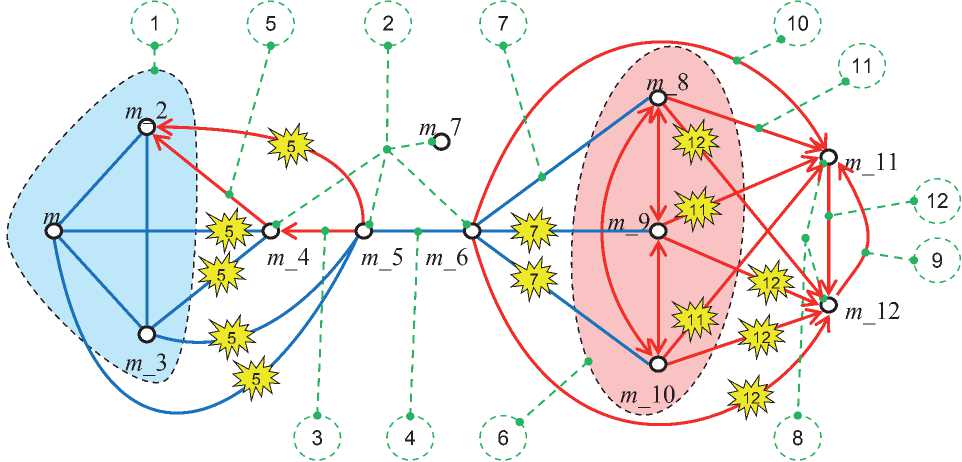
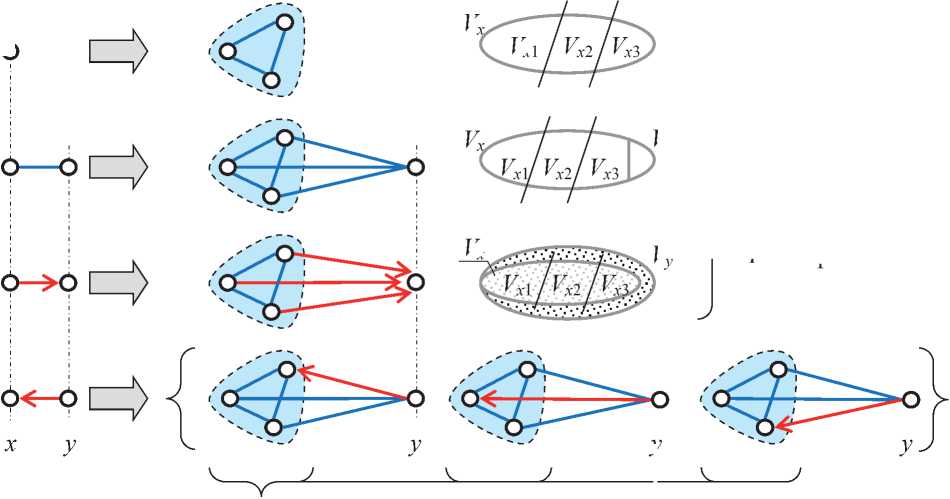
Все этапы последующего изложения иллюстрирует граф на рисунке 3, который описывает матрица инцидентности, представленная на рисунке 4.

• 1.1    Расширение набора свойств

Задача добавления множества новых свойств в набор измеряемых свойств с ОСС, когда не выдвигается требование их какой-либо сопряжённости с уже существующими в этом наборе свойствами, тривиальна. Однако постановку этой задачи можно обобщить, считая, что в добавляемом множестве свойств могут присутствовать «свои» ОСС. Поскольку акты добавления свойств и включения их в экзистенциональные отношения (добавления сопряжённостей) разумно разделять, то такое в целом полезное обобщение задачи целесообразно ограничить. Здесь во внимание следует принять когнитивный смысл расширения набора измеряемых свойств [22, 23], а также практические соображения по упрощению реализации алгоритмических примитивов, используемых при построении матрицы инцидентности, пример которой приведён на рисунке 4. С учётом этого рационально ограничиться тремя возможностями расширения набора измеряемых свойств, алгоритмы которых приводятся ниже.

• -    i -й шаг построения набора свойств и ограничений их существования;

• -    группа сопряжённых свойств как результат одного шага построения набора свойств с ограничениями существования;

• -    пометка сопряжённостей, автоматически достраиваемых в результате i -го шага построения набора свойств с ограничениями существования (здесь вследствие транзитивности обусловленности и относительной транзитивности несовместимости).

Рисунок 3 - Пример пошагового построения набора свойств с ограничениями существования (пояснение ряда графических образов см. на рисунке 1)

Алгоритм «Добавление k несопряжённых свойств», k >  1

• 1)    for i := 1 to k

• 2)      x : = new P ' P - класс «Свойство»

• 3)      M := M и { x } 'добавление свойства x в набор измеряемых свойств

• 4)    next i

Алгоритм «Добавление k взаимообусловленных свойств», k >  2

• 2)

• 3)

• 4)

• 5)

• 6)

n := | M

Добавление_k_несопряжённых_свойств 'см. описание выше for i := 1 to k for j := i +1 to k

С(M[n + i], M[n + j]) := True 'сопрягаемые свойства извлекаются из набора M С(M[n + j], M[n + i]) := True 'с помощью примитива [■] next j next i

Алгоритм «Добавление к попарно несовместимых свойств», к >  2

• 1)    n := | M

• 2)    Добавление к _несопряжённых_свойств

• 3)    for i := 1 to к

• 4)       for j := i +1 to к

• 5)         E ( Mn + i ], Mn + j ]) := True

• 6)       next j

• 7)    next i

На рисунках 3, 4 шаг 1 добавляет три попарно несовместимых свойства, шаг 2 - четыре несопряжённых свойства, шаг 6 - три взаимообусловленных (ВЗО-) свойства, шаг 8 - два несопряжённых свойства.

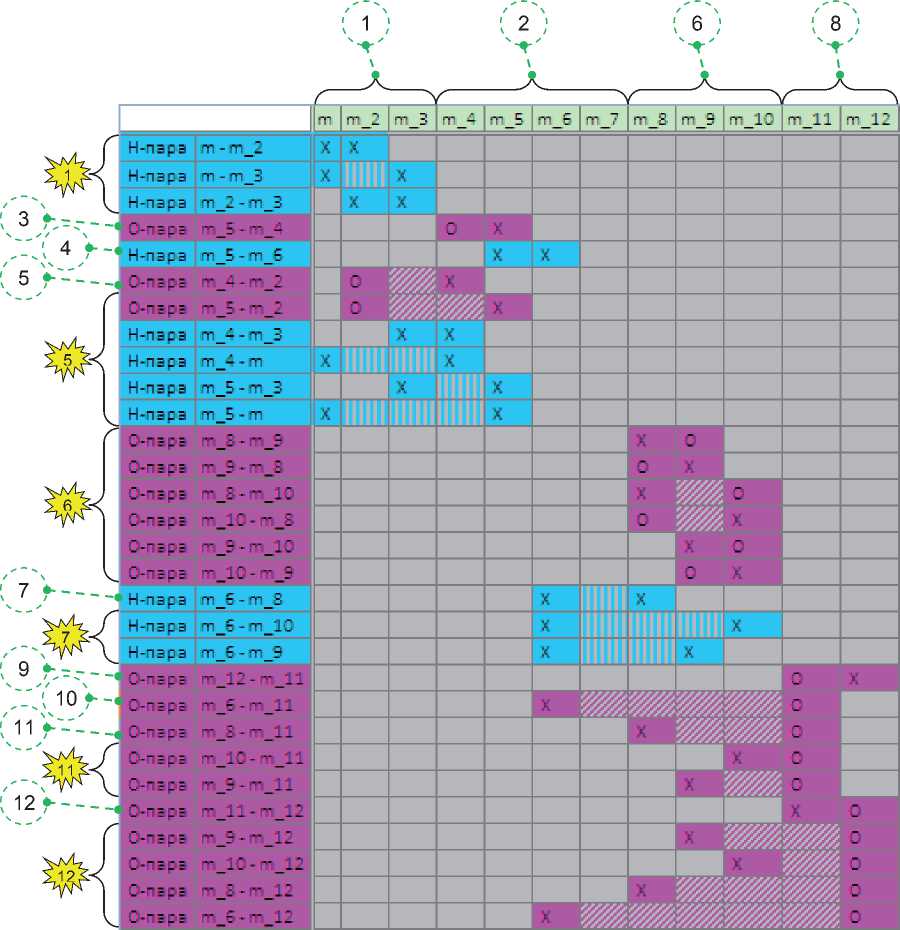
Рисунок 4 - Пример пошагового построения матрицы инцидентности «сопряжённости пар свойств - свойства», описывающей набор свойств с ограничениями существования: Н-пара - пара несовместных свойств;

О-пара - пара свойств с обусловленностью, где знак инцидентности «О» указывает обусловленное свойство (пояснение других графических образов см. на рисунке 2)

• 1.2 Добавление сопряжённости пары свойств

Желание субъекта ОАД добавить в набор ОСС сопряжённость пары свойств x , у е M -будь то обусловленность любой «направленности» (О-пара), либо несовместимость (Н-пара) - должно быть отклонено , если:

• ■    указанная сопряжённость уже существует;

• ■    указанная сопряжённость противоречит существующей сопряжённости x и у , т.е. потребована либо несовместимость x и у , а эта пара так или иначе уже состоит в отношении обусловленности, либо наоборот ( V x , у е M : Е ( x , у ) л ( С ( x , у ) v С ( у , x )) = False );

• ■    добавление указанной сопряжённости нарушит законы транзитивности экзистенциальных отношений. Нетрудно показать, что нарушение EC -транзитивности произойдёт лишь при попытке добавления в ОСС О-пары ( x , у ) в случае, когда 3 z е C ( x ) п Е(у ), а нарушение транзитивности обусловленности - при попытке добавления Н-пары ( x , у ) в случае, когда 3 z е C ( x ) п C(у ).

Сказанное вполне определяет порядок проверки допустимости добавления сопряжённости пары свойств, а собственно добавление сопряжённости пары свойств, инициированное субъектом ОАД, в общем случае вызывает необходимость добавления в ОСС других новых сопряжённостей свойств в силу транзитивности экзистенциальных отношений. Эти действия составляют содержание алгоритмов добавления О- и, отдельно, Н-пары свойств.

Алгоритм «Добавление О-пары ( x , у )», x , у е M

• 1)    if not С ( x , у ) = True and not E ( x , у ) = True and | C ( x ) п Е ( у ) | = 0 then

• 2)       C ( x ) := C ( x ) и { x } ' x и обусловливающие его свойства

• 3)      С(у ) := С(у ) и { у } ' у и обусловливаемые им свойства

• 4)     'Добавление в ОСС новых О-пар (включая указанную субъектом ОАД),

'если они там отсутствуют и речь не идёт об образовании самообусловленности; 'тем самым транзитивность обусловленности оказывается выполненной:

for each z 1 in C ( x )

• 5)          for each z 2 in С (у )

• 6)              if С ( z 1, z 2) = False and z 1 * z 2 then С ( z 1, z 2) := True

• 7)          next z 2

• 8)       next z 1

• 9)      M := 0 'начало формирования множества свойств,

'несовместимых с каждым свойством из С(у )

• 10)      for each z 1 in С(у )

• 11)         for each z 2 in Е ( z 1) M := M и { z 2} next z 2 'бесповторное добавление свойства z 2

• 12)           M := M и { z 2} next z 2 'бесповторное добавление свойства z 2

• 13)         next z 2

• 14)    next z 1

• 15)    'Добавление в ОСС новых Н-пар ( z 1, z 2) -

• 'несовместимости каждого свойства из C(x) с каждым свойством в M, 'если она в ОСС отсутствует;

'тем самым EC -транзитивность оказывается выполненной:

for each z 1 in C ( x )

• 16)         for each z 2 in M

• 17)             if E ( z 1, z 2) = False then E ( z 1, z 2) := True

• 18)         next z 2

• 19)    next z 1

• 20)    end if

На рисунках 3, 4 шаг 5 добавляет О-пару ( m _4, m _2), и для выполнения транзитивности экзистенциональных отношений автоматически добавляются О-пара ( m _5, m _2) и Н-пары ( m _4, m _3), ( m _4, m ), ( m _5, m _3), ( m _5, m ). Аналогично при добавлении О-пары ( m _8, m _11)

автоматически формируются О-пары ( m _10, m _11), ( m _9, m _11), а при добавлении О-пары ( m _11, m _12) - О-пары ( m _9, m _12), ( m _10, m _12), ( m _8, m _12), ( m _6, m _12).

Алгоритм «Добавление Н-пары ( x , у )», x , у е M

• 1)    if not E ( x , у ) = True and not ( С ( x , у ) = True or С ( x , у ) = True) and | C ( x ) n C(y ) | = 0 then

• 2)       C ( x ) := C ( x ) и { x } ' x и обусловливающие его свойства

• 3)      C ( у ) := C ( у ) ^u { у } ' У и обусловливающие его свойства

• 4)     'Добавление в ОСС новых Н-пар (включая указанную субъектом ОАД),

'если они там отсутствуют; тем самым EC -транзитивность оказывается выполненной:

for each z 1 in C ( x )

• 5)           for each z 2 in C ( у )

• 6)              if E ( z 1, z 2) = False then E ( z 1, z 2) := True

• 7)          next z 2

• 8)        next z 1

• 9)    end if

• 2.1    Удаление сопряжённости пары свойств

На рисунках 3,4 шаг 7 добавляет  Н-пару  ( m _6, m _8),  и для выполнения

EC -транзитивности автоматически добавляются Н-пары ( m _6, m _10), ( m _6, m _9).

2 Алгоритмы модификации набора свойств с ограничениями существования

В данном разделе вначале анализируются такие элементарные модификации набора измеряемых свойств с ОСС как удаление свойства из набора измеряемых свойств и удаление сопряжённости пары свойств из ОСС. Затем рассматриваются более «нагруженные» в когнитивном смысле модификации набора измеряемых свойств и ОСС, возникающие в результате концептуального шкалирования измеряемых свойств, и, наконец, замещение свойства группой взаимообусловленных свойств.

Вне сомнения, изъятие из ОСС сопряжённости свойств x , у е M чревато нарушением транзитивности экзистенциональных отношений измеряемых свойств:

• ■    транзитивность обусловленности нарушится, если из ОСС удалить О-пару ( x , y), являющуюся « замыканием » двухзвенной цепочки обусловленностей, т.е. 3 z е M , z * x , z * у : С ( x , z ) л C ( z , у ) = True ;

• ■    транзитивность несовместимости относительно обусловленности - EC -транзитивность -нарушится, если из ОСС удалить Н-пару ( x , y), являющуюся « замыканием » двухзвенной цепочки   «обусловленность-несовместимость»,   конкретно    3 z е M ,   z * x , z * у :

С ( x , z ) л E ( z , у ) v С ( у , z ) л E ( z , x ) = True (дизъюнкция в последней формуле объясняется симметричностью несовместимости пары свойств).

Таким образом, основным содержанием алгоритмов удаления сопряжённостей пар свойств из ОСС является проверка допустимости такого действия.

Алгоритм «Удаление О-пары ( x , у )», x , у е M

• 1)    if | С (у ) n C ( у ) | = 0 then 'О-пара ( x , у ) не является «замыкающей»

• 2)       С ( x , у ) := False 'удаление обусловленности свойством x свойства у

• 3)    end if

Алгоритм «Удаления Н-пары ( x , у )», x , у е M

• 1)    if | С ( у ) n E ( у ) | + | С (у ) n E ( x ) | = 0 then 'Н-пара ( x , у ) не является «замыкающей»

• 2)      E ( x , у ) := False 'удаление несовместимости свойств x и у

• 3)    end if

• 2.2    Удаление свойства

Например, в наборе свойств с ОСС на рисунке 3 попытка удаления О-пары ( m _6, m _12) или Н-пары ( m , m _5) будет отклонена, а удаление О-пары ( m _4, m _2) или Н-пары ( m , m _3) возможно.

Удаление свойства x е M - абсолютно неконфликтная модификация набора измеряемых свойств с ОСС, поскольку она предполагает удаление всех сопряжённостей этого свойства, причём отсутствие нарушений транзитивности экзистенциональных отношений измеряемых свойств гарантируется «автоформированием» условия

3 z е M, z Ф x, z Ф у: С(x, z) л C(z, у) = True, С(x, z) л E(z, у) v С(у, z) л E(z, x) = True, а удаление несопряженного свойства из набора измеряемых свойств тривиально.

Алгоритм «Удаление свойства x », x е M

• 1)    for each у in С ( x ) 'удаление сопряжения с обусловливаемыми свойствами

• 2)       С ( x , у ) := False

• 3)    next у

• 4)    for each у in C ( x ) 'удаление сопряжения с обусловливающими свойствами

• 5)       С(у , x ) := False

• 6)    next у

• 7)    for each у in E ( x ) 'удаление сопряжения с несовместимыми свойствами

• 8)       E(у , x ) := False

• 9)    next у

• 10)    M := M \ { x }

• 2.3    Когнитивное шкалирование свойств

В [22, 23] обоснована концепция, согласно которой набор измеряемых свойств с ОСС -продукт, возникающий в результате выдвижения субъектом ОАД гипотез о понятийной структуре , описывающей исследуемую ПрО.

Например, добавление в набор измеряемых свойств одного нового свойства знаменует образование множества новых гипотетических понятий, содержания которых возникают как определенные комбинаторные объекты из нового и существовавших измеряемых свойств, а также новых гипотетических понятий, обобщающих такие комбинаторные объекты.

Два (и только два) других способа формирования новых гипотетических понятий - известные в классической логике деление и ограничение существующего понятия [15, 16] - вызывают модификации набора измеряемых свойств, которые следует расценивать как соответственно дизъюнктивное и уточняющее концептуальное шкалирование свойств [22, 23]:

• ■    дизъюнктивное (номинальное) шкалирование свойства выполняется путём разделения его домена на k > 2 непересекающихся частей и приводит к замещению шкалируемого свойства набором k новых несовместимых свойств;

• ■    уточняющее (порядковое) шкалирование свойства устанавливается покрытием его домена двумя областями, первая из которых есть домен целиком, а вторая - какая-то его часть («строгая часть»). Тогда у объектов исследуемой ПрО добавляется новое свойство, которое некоторым образом определяет выделенную часть домена шкалируемого свойства и обусловливает последнее. Обобщением такого приема является уточняющее шкалирование одновременно k > 2 свойств, когда добавляемое новое свойство описывает одновременно все выделенные части (среди которых хотя бы одна строгая) доменов шкалируемых свойств и, следовательно, обусловливает все k шкалируемых свойств.

• 2.3.1    Дизъюнктивное шкалирование свойства

Анализ возможности дизъюнктивного шкалирования свойства x е M иллюстрирует рисунок 5, где, в частности, демонстрируется неопределённость результата шкалирования обусловленного свойства ( | C ( x ) | > 0), возникающая в силу EC -транзитивности отношения несовместимости свойств. Поэтому предлагается постулировать невозможность дизъюнктивного шкалирования обусловленного измеряемого свойства, и алгоритм такого шкалирования начинать с соответствующей проверки.

о

V x

V

y

V

V x 1

V y

{ x 1, x 2, x 3} - свойства, замещающие свойство x

Рисунок 5 - Пример дизъюнктивного шкалирования: замещение тремя несовместимыми свойствами { x 1, x 2, x 3} свойства x , сопряжённого со свойством у ; приведены случаи: x без сопряжения, у е E ( x ), у е C ( x ), у е C ( x ) (пояснение ряда графических образов см. на рисунке 1)

Домены свойств и их покрытия, ^ формируемые в процессе дизъюнктивного шкалирования

Алгоритм «Дизъюнктивное шкалирование свойства x с замещением шкалируемого свойства к новыми свойствами», x е M, к > 2

• 1)    if I C ( x ) | = 0 then 'дизъюнктивное шкалирование свойства x возможно

• 2)    n := | M i

• 3)     Добавление_ k _несопряжённых_свойств 'см. описание выше

• 4)    for i := 1 to к

• 5)          for each у in E ( x )

• 6)           Добавление_Н-пары_( Mn + i ], у ) 'см. описание выше

• 7)          next у

• 8)          for each у in C ( x )

• 9)           Добавление_О-пары_( Mn + i ], у ) 'см. описание выше

• 10)         next у

• 11)      next i

• 12)    Удаление.свойства_ x 'см. описание выше

• 13)    end if

• 2.3.2    Уточняющее шкалирование свойства

Анализ, аналогичный тому, что очерчен для дизъюнктивного шкалирования, позволяет установить, что невозможно реализовать обобщённую версию уточняющего шкалирования множества M с M , | M | > 2 измеряемых свойств, если хотя бы два из них несовместимы

(естественно, для уточняющего шкалирования одного свойства, т.е. при | M | = 1, последнее условие не возникает; формально это следует из антирефлексивности отношения несовместимости свойств).

Например, присутствующее на рисунке 3 множество свойств { m _4, m _5, m _6} не может быть подвергнуто уточняющему шкалированию, а множество { m _4, m _5, m 7} шкалировать таким образом допустимо.

В приводимом далее алгоритме смысл проверки возможности уточняющего шкалирования заданного множества M с M свойств передан, но её реализация может быть эффективнее, т.к. первое же обнаружение несовместимости пары свойств в M проясняет ситуацию.

Алгоритм «Уточняющее шкалирование множества свойств M *

с добавлением нового свойства», M с M , | M | >  1

• 1)    b := True 'флажок «Шкалирование возможно»

• 2)    if | M * | > 2 then

• 3)    for each x in M

• 4)          for each y e M \ {x}

• 5)             if E ( x , y ) = True then b := False

• 6)          next y

• 7)    next x

• 8)    end if

• 9)    if b = True then 'уточняющее шкалирование множества M возможно

• 10)      n := | M

• 11)    Добавление _k _несопряжённых_свойств, k = 1

• 12)     for each x in M^*

• 13)         Добавление_О-пары_( M [ n + 1], x )

• 14)      next x

• 15)    end if

• 2.4    Замещение свойства группой взаимообусловленных свойств

По определению во множестве гипотетических понятий, отвечающих формируемому субъектом ОАД набору измеряемых свойств с ОСС, содержание отдельно взятого понятия отличается от содержаний других понятий, по меньшей мере, одним свойством. Когда таких отличительных свойств в содержании какого-то понятия несколько, то в аспекте ОСС они взаимообусловлены [22]. Действительно, у всех объектов из объёма этого гипотетического понятия (и только у них среди всех объектов, гипотетически присутствующих в исследуемой ПрО) кроме, возможно, других свойств наличествуют все рассматриваемые отличительные свойства. Следовательно, устанавливая, что наблюдаемый в ПрО объект обладает любым одним таким отличительным свойством, согласно выдвинутой гипотетической картине следует констатировать, что он характеризуется и всеми остальными отличительными свойствами, и, таким образом, любое одно такое отличительное свойство обусловливает все другие, а это означает, что все обсуждаемые отличительные свойства взаимообусловлены.

Опыт показывает, что формируя гипотезы о понятийной структуре, описывающей исследуемую ПрО, субъект ОАД нередко решает, что вместо одного отличительного свойства некоторое гипотетическое понятие о ПрО должно характеризоваться несколькими, например, уточняя, что интересующие его люди должны характеризоваться не только фамилией, но и именем. Поэтому целесообразно при формировании набора измеряемых свойств с ОСС располагать возможностью замещения одного свойства группой ВЗО-свойств.

Очевидно, что в силу транзитивности экзистенциональных отношений между свойствами каждое из ВЗО-свойств, замещающих выбранное измеряемое свойство, «наследует» все его сопряжённости в наборе измеряемых свойств (это также следует из того, что отношение вза- имообусловленности Н в силу характеризующих его свойств симметрии - см. введение - разбивает множество измеряемых свойств на классы эквивалентности). Реализация наследования сопряжённостей замещаемого свойства замещающими его ВЗО-свойствами составляет основное содержание рассматриваемого алгоритма замещения.

Алгоритм «Замещение свойства x группой к ВЗО-свойств», x е M , к > 2

• 1)    Добавление к _взаимообусловленных_свойств 'см. описание выше

• 2)    y := M[n + к ] 'последнее из замещающих ВЗО-свойств,

'которое далее наследует все сопряжённости замещаемого свойства x ;

'при этом остальные замещающие ВЗО-свойства получат все эти сопряжённости 'автоматически - см. алгоритмы добавления сопряжённостей пар свойств

• 3)    for each z in С ( x )

• 4)     Добавление_О-пары_( у , z )

• 5)    next z

• 6)    for each z in C ( x )

• 7)      Добавление_О-пары_( z , y )

• 8)    next z

• 9)    for each z in E ( x )

• 10)    Добавление_Н-пары_( z , y )

• 11)    next z

• 12)    Удаление_свойства_ x

  Иллюстрацию замещения измеряемого свойства группой ВЗО-свойств можно найти на рисунке 3, если предположить, что группа ВЗО-свойств { m _8, m _9, m _10} - результат замещении некоторого «протосвойства» m _8910, которое было несовместимо со свойством m _6 и обусловливало свойства m _11, m _12.

3 Трансформация ограничений существования свойств

В отличие от метода построения онтологий, прямо основанного на анализе ОСС [17-19], в ОАД информация об ОСС используется при дефаззификации нестрогого формального контекста, который возникает вследствие неполноты и противоречивости имеющихся эмпирических данных, причём локально для каждого объекта, попавшего в поле зрения исследователя [20, 21]. Однако и та и другая методики связаны выявлением подмножеств свойств, совместимых с ОСС, т.е. нормальных подмножеств измеряемых свойств. Разбор формального определения нормального подмножества свойств (см. введение) позволяет указать в наборе свойств с ОСС субструктуры , которые будучи выявлены, открывают путь к быстрой констатации «нормальности» актуальных подмножеств измеряемых свойств³:

• ■    группа ВЗО-свойств (ВЗО-группа) принадлежит нормальному подмножеству только целиком (что естественно для отдельно взятого свойства, которое формально в силу само-обусловленности следует считать частным случаем ВЗО-группы);

• ■    группа с односторонней обусловленностью (О-группа), в которой одно свойство или, эквивалентно, группа ВЗО-свойств обусловливает другое свойство или, эквивалентно, группу ВЗО-свойств, либо входит в нормальное подмножество целиком , либо своей обусловливаемой частью . Отношение обусловленности между ВЗО-группами обобщает отношение между свойствами в том смысле, что каждое свойство-член одной группы обусловливает все свойства-члены другой (формальный анализ этого отношения можно найти в [19]);

• ■    группа попарно несовместимых свойств (Н-группа) может быть представлена в нормальном подмножестве только одним своим членом.

• 3.1    Выявление групп взаимообусловленных свойств

Таким образом, актуальна задача трансформации «естественного» представления набора измеряемых свойств с ОСС как конечного множества с заданными на нём бинарными отношениями в набор групп свойств, однородных по виду экзистенционального сопряжения свойств-членов. Решение этой задачи в форме матрицы инцидентности «однородные группы свойств - свойства» для набора свойств с ОСС, представленного на рисунках 3, 4, демонстрирует рисунок 6.

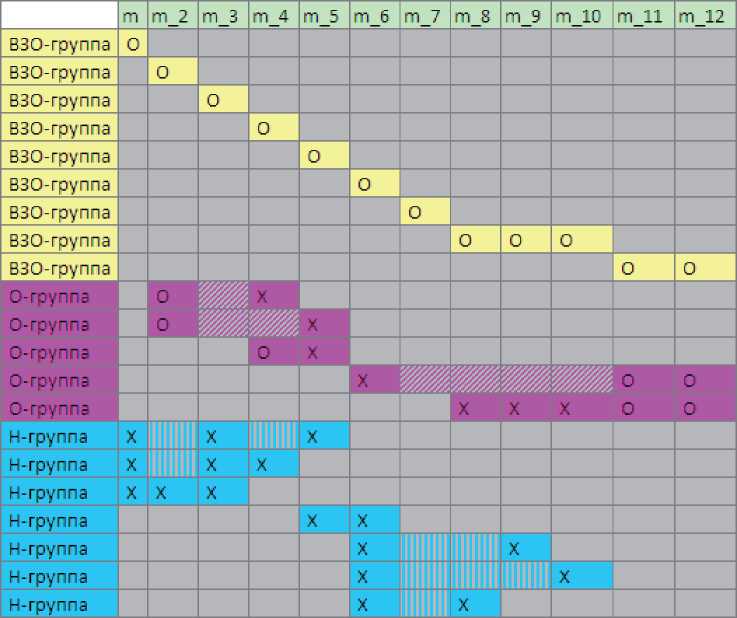
Рисунок 6 - Пример описания набора свойств с ограничениями существования в виде матрицы инцидентности «однородные группы свойств - свойства»

Во-первых, каждое в отдельности измеряемое свойство является самостоятельной ВЗО-группой. Во-вторых, ясно, что признаком ВЗО-группы является не только взаимообусловленность входящих в неё свойств, но и отсутствие пересечения с другими ВЗО-группами (исключая, разумеется, некоторые ВЗО-группы, состоящие из одного свойства). Поэтому после выявления очередной ВЗО-группы её свойства-члены следует исключить из дальнейшего анализа, что сокращает трудоёмкость выявления каждой следующей такой группы.

Алгоритм «Выявление ВЗО-групп»

• 1)    M := M 'получение копии множества свойств

• 2)    do while | M * | > 0

• 3)      x := M [1] 'очередное свойство, не состоящее в ранее выявленных ВЗО-группах

• 4)      G : = new VZO ' VZO - класс «ВЗО-группа»;

' G используется здесь лишь как множество свойств-членов группы G

• 5)      G := G и { x } ' x - ядро и, возможно, единственный член новой ВЗО-группы

• 6)    for each y in C ( х )

• 7)          for each z in C(y )

• 8)             if z = х then G := G и {у }

• 9)           next z

• 10)      next y

• 11)     M * := M * \ G

• 12)    loop 'множество свойств конечно

• 3.2    Выделение групп с односторонней обусловленностью

Поскольку по определению О-группа - это две ВЗО-группы, одна из которых обусловливает другую, то алгоритм выделения О-групп строится в предположении, что все ВЗО-группы в наборе измеряемых свойств с ОСС уже выявлены.

Алгоритм «Выявление О-групп»

• 1)    for each G 2 in VZOs 'перебор всех построенных ВЗО-групп

• ' G 2 используется здесь лишь как множество свойств-членов группы G 2

• 2)       M * := C ( G 2[1]) \ G 2

'множество свойств-членов ВЗО-групп, отличных от ВЗО-группы G 2;

'каждое из этих свойств обусловливает каждый член ВЗО-группы G 2

• 3)      for each G 1 in VZOs 'перебор всех построенных ВЗО-групп

' G 1 используется здесь лишь как множество свойств-членов группы G 1

• 4)         if | G 1 n M | > 0 then 'ВЗО-группа G Обусловливает ВЗО-группу G 2

• 5)             G : = new O ' O - класс «О-группа»

• 6)            G. C : = G 2 'обусловливаемые свойства-члены О-группы

• 7)            G.C : = G 1 'обусловливающие свойства-члены О-группы

• 8)           end if

• 9)       next G 1

• 10)    next G 2

• 3.3    Выявление групп попарно несовместимых свойств

Проблемой выявления Н-групп в наборе измеряемых свойств с ОСС является не только их пересечение между собой, но, прежде всего, вложенности одних таких групп в другие -как правило, подобные структуры эффективно обрабатываются лишь путём рекурсии. Например, на рисунке 3 Н-группы { m , m _2, m _3} и { m , m _3, m _5} пересекаются, а в Н-группу { m , m _2, m _3} вложены Н-группы { m , m _2}, { m , m _3}, { m _2, m _3}.

Алгоритм «Выявление Н-групп»

• 1)    for each x in M

• 2)      G := Ассоциированные^_ х _Н-группы

'множество Н-групп, каждая из которых включает свойство х и 'определённое подмножество попарно несовместимых с ним свойств 3)      Ns := Ns и G 'бесповторное (по составу свойств-членов) накапливание Н-групп

• 4)    next x

Алгоритм рекурсивной функции «Ассоциированные_с_ х_ Н-группы» выявляет как все пересекающиеся, так и вложенные одна в другую Н-группы, включающие в себя свойство х .

Алгоритм «Ассоциированные с х Н-группы», х е M

• 1)    Gs : = 0 'множество Н-групп, ассоциированных со свойством х

• 2)    for each y in E ( х )

• 3)      M := E(y ) n E ( х ) 'свойства, несовместимые как со свойством y , так и со свойством х

• 4)      if \M\ < 1 then ' M пусто или содержит одно свойство

• 5)         G : = new N ' N - класс «Н-группа»

' G используется здесь и как множество свойств-членов группы G

• 6)          G : = G и { y }

• 7)          if | M^* | = 1 then G : = G ∪ M^*

• 8)        else

• 9)         G : = Ассоциированные с y Н-группы 'рекурсия для свойства y

• 10)      end if

• 11)     Gs : = Gs ∪ G 'бесповторное накопление Н-групп

• 12)    next z

• 13)    for each G in Gs

• 14)    G : = G ∪ { x }

• 15)    next G

• 16)    Ассоциированные с x Н-группы : = Gs

Заключение

Представленные в статье алгоритмы формирования набора свойств, подлежащих измерению у объектов исследуемой ПрО, с набором ограничений существования этих свойств призваны обеспечить поддержку и сохранение результатов априорных когнитивных актов субъекта, намеревающегося получить данные измерений, а затем формально вывести из этой эмпирической информации онтологическую модель интересующей его ПрО. Полнота, достаточность и эффективность алгоритмической поддержки этой деятельности субъекта-исследователя достигнута как за счёт теоретического обоснования логического смысла рассматриваемых актов, так и благодаря целесообразному ограничению мыслимых возможностей такой поддержки.

Алгоритмы трансформации исходного «естественного» представления набора измеряемых свойств с ограничениями существования в набор субструктур, однородных по виду эк-зистенционального сопряжения свойств-членов, обеспечивают возможность эффективного практического использования априорных соображений субъекта онтологического анализа эмпирических данных. Основанием для такого вывода является возможность прямого соотнесения внутреннего устройства названных субструктур с прагматически важным и теоретически строгим понятием нормального подмножества измеряемых свойств.

Представленный в статье комплекс алгоритмов предполагается реализовать в разрабатываемой в Институте проблем управления сложными системами РАН системе онтологического анализа данных на массовой программной платформе.

Работа выполнена при финансовой поддержке Министерства науки и высшего образования Российской Федерации (регистрационный номер НИОКТР АААА-А19-119030190053-2).