Алгоритмизация учебной деятельности при изучении систем обыкновенных дифференциальных уравнений первого порядка

Актуализация практической направленности математических задач, предлагаемых студентам инженерных специальностей в техническом вузе, является одной из насущных проблем современного математического образования в высшей школе, решение которой повышает мотивацию студентов-будущих инженеров к изучению предмета. Данный подход соотносится с общими целями и задачами подготовки инженерно -технических работников высшей квалификации, успешная реализация которых возможна в рамках системной учебной деятельности, рассчитанной как на ближнюю, так и на отдалённую перспективу.

Важнейшим компонентом комплексной учебной деятельности является систематизация её приёмов, базирующаяся на общедидактических принципах и дополняемая рядом особенностей конкретной предметной дисциплины. А для «точных наук», в которых основная форма познавательной и исследовательской деятельности лежит в области решения математических задач, особое значение приобретает процедура алгоритмизации - как начальный этап обучения студентов решению задач различных типов по изучаемой теме.

В области математических наук для инженерных специальностей можно воспользоваться следующими функциями систематизации учебной деятельности, предложенными Е.И. Саниной в её докторской диссертации «Методические основы обобщения и систематизации знаний учащихся в процессе обучения математике в средней школе»: фундаментализации знаний, трансформации, развивающего обучения, культурологическая, аналитическая, корректирующая, образовательная, обобщения и приобретения правильного навыка, пополнения системы, свёртывания, преобразовательная, контроля правильности решения, доверия в математическую модель, исследовательская (см. боле подробно с примерами в [1, с. 156-165]).

Очевидно, что при освоении той или иной темы преподавателю не обязательно использовать все четырнадцать предложенных функций, однако если при выстраивании методики ознакомления студентов с новым учебным материалом он находит необходимым и возможным выделить хотя бы некоторые из них в самостоятельные этапы алгоритма усвоения, то подобную стратегию учебно-познавательной деятельности следует отнести к одной из наиболее продуктивных.

Покажем на примере изучения раздела «Решение систем обыкновенных дифференциальных уравнений первого порядка» процедуру алгоритмизации как средства формирования приёмов учебной математической деятельности с ориентацией на практическую составляющую

Этап 1 выполняет аналитическую функцию, цель которой -ознакомить студентов с многообразием практических задач, решаемых с помощью обыкновенных дифференциальных уравнений или систем двух дифференциальных уравнений. Среди подобных приложений можно продемонстрировать законы горизонтального движения тела по его скорости или ускорению; закон движения пули, выпущенной с заданной скоростью вертикально вверх; определение температуры тела при нагревании или охлаждении; изменение массы радиоактивного вещества от скорости распада во времени; моделирование процесса гармонических колебаний подвешенного на пружине груза; моделирование процесса размножения бактерий; протекание жидкости сквозь отверстие заданного размера и другие занимательные природные или рукотворные явления и процессы [3]. Полезно бывает предложить студентам «разложить» приведённые примеры по предметным областям или, наоборот, скомпоновать их в соответствии с кругом проблем в межпредметных отраслях знаний.

Этап 2 выполняет образовательную функцию, поскольку предоставляет студентам возможность освоить практические навыки аналитического решения системы двух обыкновенных дифференциальных уравнений первого порядка, привязанной к той или иной практической задаче. Именно на этом этапе наиболее полно реализуется система учебных действий, получившая название алгоритмизация.

Прежде всего, следует обратить внимание студентов на тот факт, что специфика подобных систем уравнений состоит в том, что её числовые решения образуют упорядоченную совокупность (семейство) бесконечного множества изображающих точек на фазовой плоскости (ФПл), движущихся по фазовым траекториям относительно точек бифуркации системы, называемых особыми точками (ОТ). Поэтому решение системы дифференциальных уравнений, полученное аналитическим способом, являет собой фазовый портрет (ФПр) соответствующей динамической системы на ФПл.

ПРИМЕР [2, с. 402-404].

Решить систему дифференциальных уравнений:

(х = - 2х + 5у

(j = х + 2у.

• 1)    Определение координат и типа ОТ.

Очевидно, что координаты ОТ (x;у) = (0;0). Собственные значения системы (1), или характеристические числа λ1,2, устанавливающие тип ОТ на ФПл, находим как корни уравнения, получаемого из соответствующего определителя системы:

det

(A

–

λ       I )

0,

где А = (—2  5) - квадратная матрица коэффициентов линейных уравнений системы (1), а I = (l) - единичная матрица-столбец. Тогда уравнение (2) примет вид:

(—2—Л 5 \

⁽ l    2 — A)

Характеристические числа системы (1) являются корнями квадратного уравнения, полученного из (3): (– 2 – λ) • (2 – λ) – 5 = 0, и соответствуют ОТ типа «седло» (поскольку λ1,2 = ± 3 – действительные числа разных знаков), которая всегда является точкой неустойчивого равновесия.

• 2) . Определение собственных векторов системы (1).

Для анализа изменения параметров системы (1) с ОТ типа «седло», необходимо найти собственные векторы системы V 1,2 , задающие направление сепаратрис седла, число которых как скалярных объектов совпадает с количеством характеристических чисел. В векторном представлении для λ < 0 обе сепаратрисы направлены к седловой ОТ, то есть являются устойчивыми, а для λ > 0 – исходят из седловой ОТ, то есть являются неустойчивыми. Уравнения для сепаратрис находятся из значений собственных векторов системы.

Элементы матриц собственных векторов

V 1 = ( i' ll ) Для ^ и V 2 = C v iz ) Для ^

определяются как корни уравнений с известными А , I и λ 1,2 :

( A – λ 1 I ) V 1 = 0 ;

( A – λ 2 I ) V 2 = 0 .

Представляя уравнения (4) и (5) в матричной форме, получаем:

(—2

—

A_l     5

l     2 —

A i ) ⁽ ^м )   0;

(-2-Я ,

-

Л,) (у,^

Проводя соответствующие преобразования уравнений (6) и (7), для каждого значения характеристических чисел λ1,2 получаем по два равнозначных уравнения, задающих один и тот же собственный вектор, что позволяет в реальных расчётах рассматривать только одно уравнение для каждого характеристического числа.

Итак, для 1 1 = +3 имеем: - 5 V 11 + 5 V 21 = 0, или V 11 — V 21 = 0 ;

налогично для 1 2 = - 3: V 21 + 5 V 22 = 0 , или V 21 + 5 V 22 = 0 .

Это замечательное свойство собственных векторов, соответствующих одному и тому же характеристическому числу, называемое коллинеарностью, упрощает поиск уравнений для сепаратрис седла. Действительно, если положить V21 = 1 и V22 = 1, то для системы уравнений (1) имеем: V1 = (у^) = (1) и V2 = С'22) =

( ^⁵) . Тогда выражения для сепаратрис можно найти по формулам: у 1 =

X            X

— и у₂ = ---, которые справедливы для ненулевых значений

^Г11     '        ' 12

коэффициентов при x и y : y 1 = x при 1 1 = +3 и у₂ = - 0,2 x при 1 2 = - 3 .

Отметим, что функцию этого этапа можно назвать корректирующей через понимание [1, с. 156], поскольку предложенный алгоритм решения, использующий свойство коллинеарности собственных векторов системы, является наиболее оптимальным способом нахождения сепаратрис.

• 3) . Построение фазового портрета системы (1).

Построение ФПр динамической системы, описываемой системой дифференциальных уравнений, позволяет визуализировать «работу» системы и развивает умение студентов моделировать реальные процессы, описываемые с помощью дифференциальных уравнений. В ходе освоения соответствующих умений рекомендуется отработать построение ФПр для различных видов систем дифференциальных уравнений «вручную» с тем, чтобы студенты могли в наглядной форме проводить сопоставление различных типов ОТ между собой, делать вывод об их статусе (устойчивости/неустойчивости), прорисовывать фазовые траектории на ФПл.

Этап 3 выполняет операциональную функцию , которая предоставляет студентам дополнительные интерактивные инструменты построения ФПр. С этой целью могут быть использованы различные пакеты прикладных программ - таких, например, как MatLab, Maxima , R , PhaPl, библиотек языка Python [2; 4]. Динамическая интерпретация численных решений систем дифференциальных уравнений на ФПл с помощью интерактивных программных платформ позволяет повысить скорость изучения различных типов систем дифференциальных уравнений с целью их сопоставления, а визуальный ряд получаемых ФПр ещё раз подчёркивает не воображаемую, а реальную красоту математических операций.

Фазовый портрет системы (1), полученный в программной среде PhaPl, изображён на рис. 1.

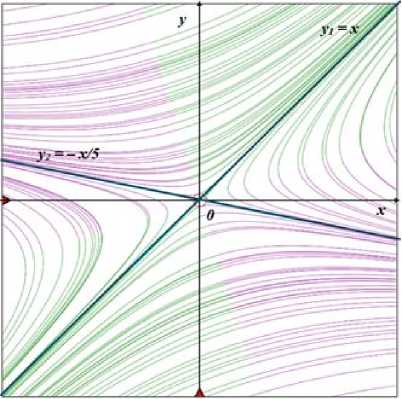
Рис. 1. Фазовый портрет системы линейных дифференциальных уравнений (1), построенный с помощью программы PhaPl

Этап 4 . Предыдущий этап, реализующий операциональную функцию, связан с функцией, называемой исследовательской , поскольку с помощью пакетов прикладных программ, позволяющих «одним кликом»

строить ФПр различных систем, можно составить целый банк систем уравнений и классифицировать их по типам ОТ, а также проследить характер изменения фазовых траекторий при варьировании параметров динамической системы.

Этап 5 может служить завершающим этапом, выполняющим функцию обобщения и приобретения правильного навыка . На этом этапе производится промежуточная проверка усвоения студентами предъявляемого учебного материала на основе накопленного опыта аналитических способов решения систем двух обыкновенных дифференциальных уравнений первого порядка (этап 2), а также проведённых ими самостоятельных исследований (этапы 3-4).

Очевидно, что систематизация приёмов учебной математической деятельности по изучаемой теме на этом не заканчивается: в статье представлен лишь возможный способ организации работы на начальной ступени. Следующий набор этапов целесообразно открыть функцией преобразовательной и функцией доверия в математическую модель .