Алгоритмы для реализации функционала объектно-ориентированного подхода к синтезу геометрических параметров зубчатой передачи

В настоящее время проектирование изделий выполняется в основном большинстве случаев с применением CAD/CAM/CAE-сред, без данных программных продуктов невозможно выполнить разработку современных высокотехнологичных изделий, в том числе приводов специального назначения.

При этом известно, что качество получаемых изделий на этапе проектирования с САПР определяется адекватностью математических моделей, заложенных в их основу, в том числе и математических моделей описания геометрии зубчатых передач. В работах [1-3] доказано, что наиболее современным представлением зубчатого профиля формообразуемого методом обкатки является использование теории огибающих кривых.

Однако применение данного метода описания зубчатого профиля в практике проектирования сдерживается сложностью описания профиля в виде систем параметрических уравнений, описывающих участки профиля зуба зубчатого колеса (рабочая поверхность, переходная кривая, впадина). Но при использовании ресурсов современных вычислительных машин и объектно-ориентированных языков программирования появилась возможность разрабатывать программное обеспечение, при этом инкапсулируя сложные вычисления от проектировщика, тем самым предоставляя возможность работать с простыми инструментами, внутри которых – 632 – заложены сложные математические модели расчетов, применяемых при проектировании современных изделий.

В работах [3-5] предложено описание составляющих профиля зубьев, которое позволяет исследовать характеристики передачи с использованием средств САПР. Однако эти модели не дают возможность в автоматизированном режиме определять ряд ключевых параметров: граничные условия при совместном решении систем уравнений, описывающих впадину, выкружку и рабочий профиль, а также экспортировать геометрию в САПР [6].

Описанные в данной работе алгоритмы позволяют решить вышеуказанные задачи и применить предлагаемые математические модели описания профилей зубчатых передач в практике проектирования изделий. Реализация данных алгоритмов выполняется в рамках работы над объектно-ориентированным подходом к синтезу геометрических параметров цилиндрических зубчатых передач. При этом алгоритмы входят в состав объектно-ориентированной модели процесса взаимодействия зубчатых передач [7] для реализации функционала объектноориентированной модели в совокупности с математической моделью из работы [3].

Алгоритмы численного нахождения граничных точек кривых, образующих профиль зубчатых пар

По математическим моделям, взятым из работы [3], профиль зубчатого колеса представляет собой совокупность кривых, представленных в виде формул. На рис. 1 представлено изображение впадины зуба, состоящего из набора кривых: 1 – окружность дна впадин, 2 – выкружка, 3 – кривая рабочей поверхности, 4 – окружность вершин. Для получения профилей зубчатых колес необходимо численными методами получить граничные условия для данных кривых, которые представляют собой, как правило, последовательно места касания данных кривых между собой; при этом параметры не зависят друг от друга и не равны друг другу в точке общего касания кривых. В этом заключается основная сложность вычисления данной точки и значений граничных параметров кривых.

Каждая из этих кривых (рис. 1) представлена функциями в параметрическом виде, которые зависят от параметра t . Следуя этому условию, обозначим граничные значения параметров, которые необходимо вычислить: t₀₀ и t₀₁ – начальное и конечное значение параметра функции 1; t V0 и t V1 – начальное и конечное значение параметра функции 2; t R0 и t R1 – начальное и конечное значение параметра функции 3; t₁₀ и t₁₁ – начальное и конечное значение параметра функции 4.

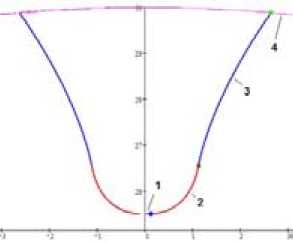
Рис. 1. Кривые, описывающие профиль зуба

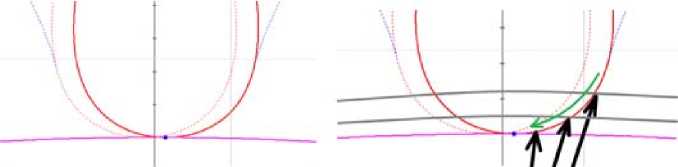
Рис. 2. Точка касания переходной кривой и окружности впадины зуба (слева) и схема вычисления точки касания переходной кривой и окружности впадин (справа)

Вычисление граничных значений кривых, описывающих профиль зуба, в данной работе предлагается вычислять численно.

Вычисление граничных значений кривых состоит из трех этапов. На первом этапе идет вычисление граничных значений окружности впадины и переходной кривой в месте их касания. Вторым этапом выполняется вычисление граничных значений функций, описывающих переходную кривую и кривую профиля рабочей поверхности в местах их касания. На последнем этапе производится вычисление граничных значений функций, описывающих профиль рабочей поверхности и окружность вершины зуба в месте их пересечения.

На риc. 2 (слева) представлено изображение переходной кривой и окружности впадины зуба, а также точки их взаимного касания.

Так как переходная кривая лишь касается, но не пересекает окружность впадины, предлагается искать точку касания методом вычисления длины радиус-вектора для точки переходной кривой и сравнением длины этого вектора с радиусом окружности впадины зуба. В момент касания переходной кривой и окружности впадины зуба длина радиус-вектора и радиус окружности впадины будут совпадать (рис. 2, справа). Таким образом, в данной точке, зная значение параметра, от которого зависит значение координаты точки переходной кривой, получаем решение задачи в виде вычисленного граничного параметра функции tV0. Граничный параметр окружности переходной кривой вычисляется по формуле t01 = arctg(x/ y), где x и y – координаты точки касания.

Вычисление осуществляется методом половинного деления отрезка с применением алгоритма для возврата на два шага назад для более точного поиска решения.

Алгоритм вычисления граничных параметров функций переходной кривой и окружности впадины зуба представлен на рис. 3. Выполнение данного алгоритма начинается с установки начального значения функции, описывающей переходную кривую. Далее следует действие выбора направления обхода функции переходной кривой: если функция описывает петлю, выбирается обратное направление обхода. Далее выполняется вычисление радиуса окружности впадины зуба, вычисление длины радиус-вектора при начальном значении параметра функции. После этого начинается выполнение цикла обхода значений переходной кривой до момента, когда значение длины радиус-вектора не станет равным (или в данном случае не будет отличаться на 1 мкм) радиусу окружности впадины зуба. После завершения работы цикла про- – 634 –

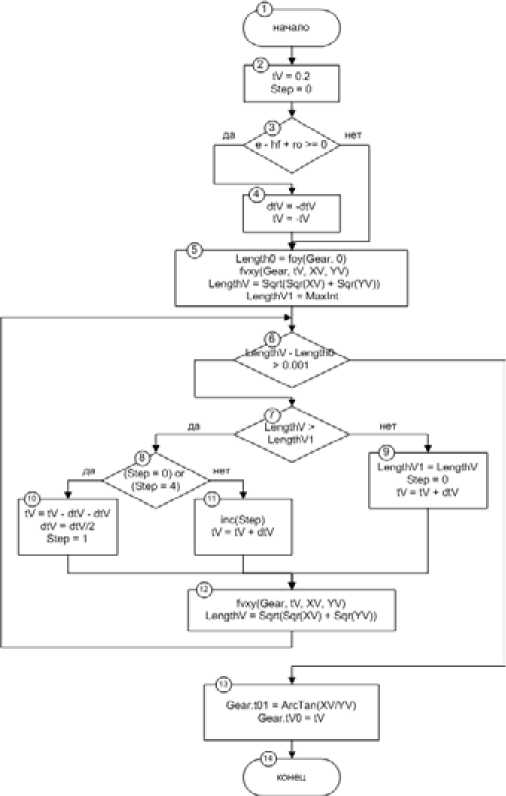
Рис. 3. Алгоритм вычисления точки касания переходной кривой и окружности впадин изводится вычисление и запись граничного параметра окружности впадины зуба t01 и запись граничного параметра tV0.

В ходе вычисления граничных значений функций, описывающих переходную кривую и кривую профиля рабочей поверхности зуба, необходимо вычислить граничный параметр t_V1, который служит граничным параметром функций переходной кривой и обозначает ее конец; а также параметр t_R0, являющийся граничным параметром функций профиля рабочей поверхности зуба, обозначающий ее начало.

Так как точка минимума функции профиля рабочей поверхности зуба находится ниже точки взаимного касания с функцией переходной кривой профиля, то вычисление точки взаимного касания начинается с вычисления точки минимума кривой профиля рабочей поверхности.

Как и в случае с вычислением точки касания функции переходной кривой и окружности впадин зуба, вычисление производится методом половинного деления путем сравнения длин – 635 – радиус-векторов в каждой последующей точки функции (рис. 4, справа). В момент, когда длина радиус-вектора станет минимальна, будет найдена точка минимума функции профиля рабочей поверхности зуба. В полученной точке запоминаем параметр tRmin. Значение данного параметра будет являться начальным значением функции при вычислении точки взаимного касания с функцией переходной кривой.

Алгоритм вычисления точки минимума функции профиля рабочей поверхности зуба начинается с установки начальных значений параметра и величины шага, а также вычисления длины радиус-вектора в точке с начальным параметром функции. Следующий этап алгоритма – выполнение цикла перебора значений функции и вычисления значений длин радиус-векторов для сравнения со значением на предыдущей итерации. Данный цикл основан на

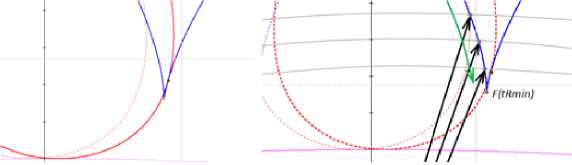
Рис. 4. Точка касания переходной кривой и кривой профиля рабочей поверхности зуба (слева) и схема вычисления минимума функции профиля рабочей поверхности зуба (справа)

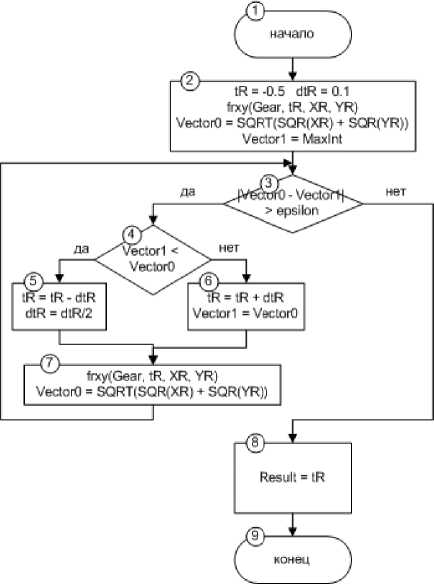
Рис. 5. Алгоритм вычисления минимума кривой профиля рабочей поверхности зуба применении метода половинного деления. После вычисления минимального значения длины радиус-вектора сохраняется значение параметра функции tRmin для применения его в вычислении точки взаимного касания с функцией переходной кривой.

Однако бывают случаи, когда значение минимума функции рабочей поверхности находиться ниже окружности впадины зуба. Поэтому для уменьшения времени вычисления минимальное значение параметра функции будет целесообразно взять t Rmin2 (рис. 6).

Для вычисления t Rmin2 выполняется перебор значений функции профиля рабочей поверхности зуба до пересечения с окружностью впадины зуба. Это вычисление также производится методом половинного деления отрезка и путем сравнения длин радиус-векторов в каждой точке функции.

Для вычисления t_Rmin2 разработан алгоритм с проверкой на пересечение функцией профиля рабочей поверхности окружности впадины зуба. Если функция пересекает окружность выполняется цикл с перебором значений функции до момента, пока длина радиус-вектора не сравняется с величиной окружности впадины зуба колеса. Алгоритм представлен на рис. 7. Результатом работы данного алгоритма является значение t_Rmin2, которое используется в качестве начального значения при вычислении точки взаимного касания с функцией переходной кривой.

Вычисление точки взаимного касания функций переходной кривой и профиля рабочей поверхности происходит с помощью перебора значений функции профиля рабочей поверхности, начиная с t Rmin (или t Rmin2 ).

После получения точки функции профиля рабочей поверхности зуба вычисляется длина радиус-вектора для данной точки. После этого производится перебор значений функции переходной кривой до момента, когда длина радиус-вектора из точки переходной кривой не будет равна длине радиус-вектора из точки на кривой профиля рабочей поверхности зуба. Когда найдены точки, лежащие на одной окружности (так как равны длины радиус-векторов), по координатам точек вычисляется расстояние между ними. После чего происходит получение следующей точки на кривой профиля рабочей поверхности и аналогично вычисляется расстояние между точками на окружности. Данный цикл повторяется до того, как расстояние между точками на окружности между кривыми не будет меньше 1 мкм (рис. 8).

После того как выполнено условие совпадения точек кривых, значение параметра переходной кривой записывается как конечное граничное значение функции t_V1, а значение параметра кривой профиля – как начальное граничное значение функции t R0 .

Алгоритм вычисления точки взаимного касания переходной кривой и профиля рабочей поверхности зуба представлен на рис. 9. В начале его работы устанавливаются начальные зна-

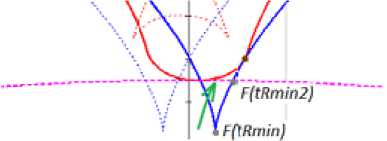
Рис. 6. Случай пересечения кривой профиля рабочей поверхности зуба окружности впадины зуба

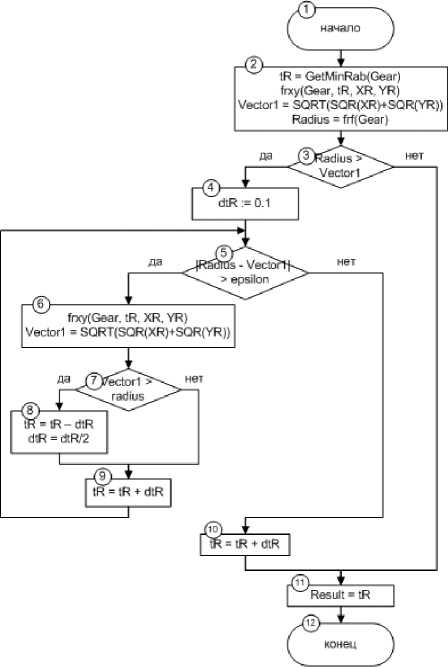
Рис. 7. Алгоритм вычисления параметра t _Rmin2

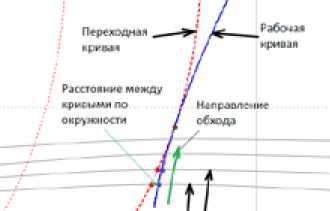
Рис. 8. Схема вычисления точки взаимного касания переходной кривой и профиля рабочей поверхности зуба чения шага перебора значений функции профиля рабочей поверхности зуба. После этого производится вычисление tRmin. Следующим действием выполняется вычисление координат точки профиля рабочей поверхности, длины радиус-вектора. По длине радиус-вектора вычисляют параметр tV переходной кривой на окружности, координаты точки на переходной кривой и расстояние между точками кривых на окружности с радиусом, равным длине радиус-вектора, для точки на кривой рабочего профиля.

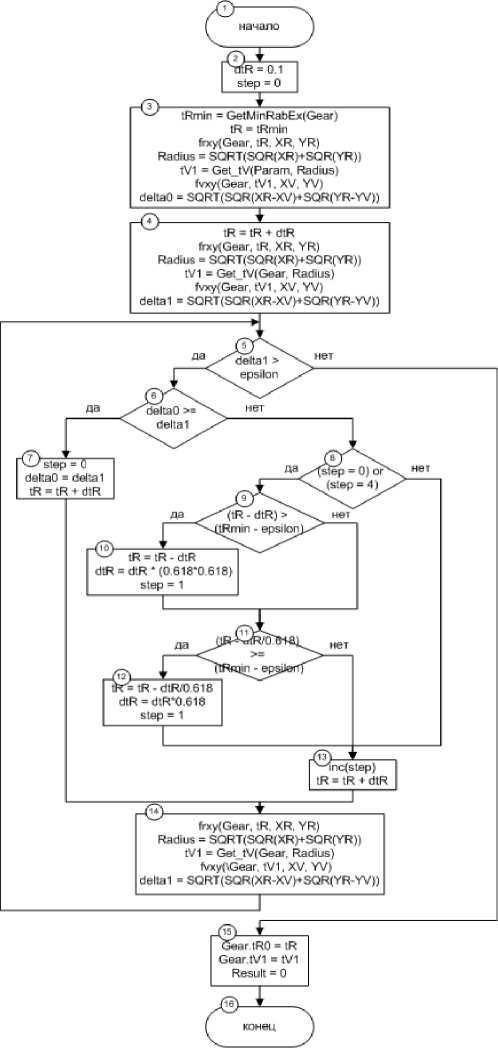
Рис. 9. Алгоритм вычисления точки взаимного касания переходной кривой и профиля рабочей поверхности зуба

Затем выполняется вторая итерация вне цикла. После чего запускается цикл поиска точки взаимного контакта кривых. Данный цикл основан на применении метода золотого сечения и возврата на два шага назад для получения более точного значения. После выполнения данного цикла сохраняются значения граничных условий функций t R0 и t V1 .

Вычисление точки пересечения кривой профиля рабочей поверхности и окружности вершин зуба (рис. 10) выполняется перебором значений функции профиля рабочей поверхности зуба начиная с параметра t_R0 .

Это вычисление производится методом половинного деления отрезка, а также путем сравнения длин радиус-векторов в каждой точке функции с радиусом окружности вершин зуба (рис. 11).

Алгоритм основан на применении перебора значений функции и метода деления отрезка пополам. Результатом выполнения данного алгоритма является конечное граничное значение

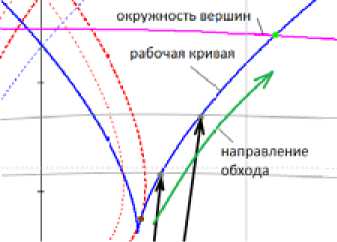
Рис. 10. Схема вычисления точки пересечения кривой профиля рабочей поверхности и окружности вершин зуба

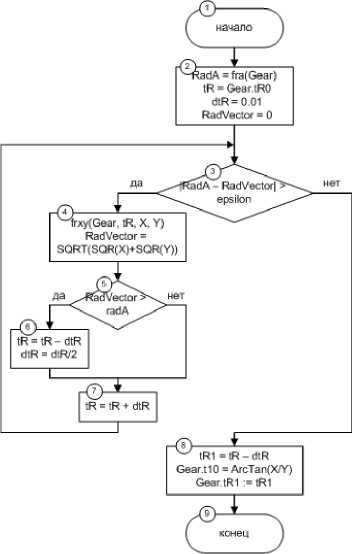
Рис. 11. Алгоритм поиска точки пересечения кривой профиля рабочей поверхности и окружности вершин окружность вершин

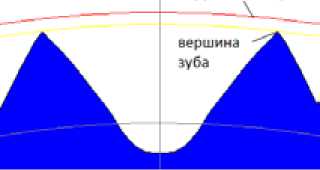
Рис. 12. Заострение зуба параметра функции профиля рабочей поверхности зуба tR1 и начальное граничное значение параметра окружности вершин зуба t10.

При больших положительных значениях коэффициента смещения исходного контура происходит заострение зуба. В этом случае кривая профиля рабочей поверхности зуба не доходит до окружности вершин зуба, а заканчивается раньше (рис. 12).

Чтобы учесть данный эффект, был разработан алгоритм, выполняющий вычисление конечного граничного параметра функции профиля рабочей поверхности зуба с учетом заострения зуба.

Основан данный алгоритм на проверке перехода угла половины зуба точкой с конечным граничным параметром функции профиля рабочей поверхности зуба.

arctg ( x / y ) >  — ,                                                            (1)

z где x и y – координаты точки с граничным конечным параметром функции профиля рабочей поверхности зуба; z – количество зубьев колеса.

Если выполняется условие 1, то начинает работать цикл по перебору значений функции в обратном направлении, который завершает свою работу, когда перестает выполняться это условие.

Результатом работы данного алгоритма является уточненное значение конечного граничного параметра функции профиля рабочей поверхности зуба t R1 .

Приведенные методики и алгоритмы вычисления граничных условий разработаны для зубчатых колес с внешним зацеплением, но с небольшими изменениями они подходят и для зубчатых колес с внутренним зацеплением.

Апробация предлагаемых алгоритмов

Предлагаемые алгоритмы численного вычисления значений граничных параметров кривых из работы [3] были реализованы в программном комплексе GearAnalysis [8, 9].

В качестве объекта для исследования была взята быстроходная ступень привода космического аппарата для поворота антенны. На рис. 13 приведена кинематическая схема привода. Параметры зубчатой передачи: z 1 =23, z 2 =44, m=0,3, n 1,2 =7-F.

По предлагаемым алгоритмам для данной передачи был выполнен расчет значений граничных параметров функций.

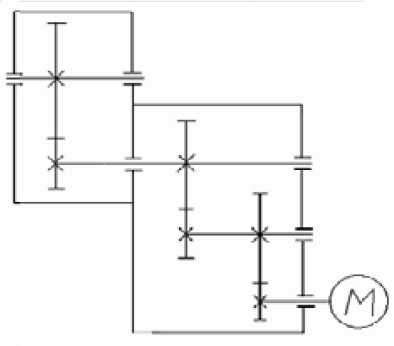
Рис. 13. Кинематическая схема привода поворота антенны космического аппарата

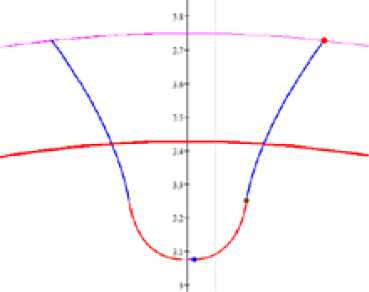
Рис. 14. Кривые, описывающие профиль зуба шестерни с граничными точками, полученными по предлагаемым алгоритмам

Для шестерни результаты расчетов значений граничных параметров составили: t₀₀ =0.00, t 01 =0.0090125, t V0 =0.00, t V1 =-0.2025, t R0 =-0.1986098, t R1 =0.2851402, t 10 =0.1080127, t 11 =0.136591, радиус окружности вершин R_a =3.75 мм, радиус окружности впадин R f =3.07 мм.

Для колеса: t 00 =0.00, t 01 =0.0044523, t V0 =0.00, t V1 =-0.1025, t R0 =-0.1080134, t R1 =0.1569866, t 10 =0.0542687, t 11 =0.0713998, радиус окружности вершин R a =6.90 мм, радиус окружности впадин R f =6.22 мм.

После выполнения расчета значений граничных параметров кривых (рис. 14) было выполнено построение зубчатой передачи, результат построения показан на рис. 15. Кроме того, на данном рисунке можно видеть изображение точек контакта (4 точки) и линии зацепления, вычисление которых выполняется по специальным численным алгоритмам, которые будут опубликованы в следующих работах.

Заключение

Предлагаемые алгоритмы реализованы в программном комплексе для синтеза геометрии и моделирования взаимодействия, в том числе разномодульных, зубчатых пар внешнего и внутреннего зацепления GearAnalysis, основанного на объектно-ориентированной – 642 –

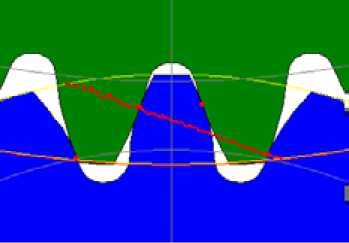
Рис. 15. Изображение зубчатой передачи в программном комплексе GearAnalysis модели процесса взаимодействия зубчатых передач [7], с программным модулем экспорта в CAD-среды [10].

В результате, после того как были разработаны данные компоненты, был реализован программный инструментарий в виде программного комплекса для выполнения проектирования зубчатых передач внешнего и внутреннего зацепления, в том числе с малой разностью чисел зубьев [11, 12].

Предлагаемые алгоритмы и сама методика проектирования зубчатых передач были апробированы в ходе выполнения разработки изделий с высоким коэффициентом тяги, в основе механизма которых лежит использование зубчатой передачи внутреннего зацепления с малой разностью чисел зубьев [13, 14]. Данные изделия были изготовлены, выполним проверку их работоспособности в ходе численных и натурных экспериментов.

В ближайших работах будет опубликовано решение задачи, связанной с поиском точек и пятна контакта. Данные задачи активно исследуются другими авторами, в частности [15, 16], однако они в своих работах используют CAE-комплексы в качестве инструмента для получения результатов; мы же будем использовать CAE-среды в качестве инструмента для проверки полученных результатов.

Кроме того, ставятся задачи развития методики проектирования зубчатых передач в направлении разработки модулей силового анализа к разработанному программному комплексу GeasAnalysis, а также разработки программных модулей с библиотеками зубонарезных инструментов.