Алгоритмы фазочастотного прослеживания сейсмических сигналов с равновесной и неравновесной обработкой

Прослеживание сейсмических волн и границ является одной из главных задач структурной сейсморазведки и прогноза геологического разреза. В общей постановке в задачу прослеживания входят обнаружение волн, их идентификация и оценка параметров. Основными неизвестными параметрами при прослеживании волн являются моменты их прихода. На основе результатов прослеживания выходных данных осуществляется построение структурных карт, а также детальное изучение геометрических параметров и формы выделяемых локальных геологических объектов [1].

На практике достаточно часто необходимо решать задачи прослеживания волн в условиях их интенсивной интерференции при наличии нерегулярных помех. Такая ситуация наиболее характерна при исследованиях тонкослоистых сред. При этом, как правило, прослеживание волн осуществляется в условиях, когда форма сигналов неизвестна. В таких ситуациях для решения задач прослеживания наиболее эффективными являются методы определения временного положения сигналов, использующие только априорную информацию об их фазовых спектрах. В фазу сигналов, точнее, в сложный закон изменения их фазовых спектров заложена информация, позволяющая в условиях существующей априорной неопределенности свойств сигнала и наличия большого числа негативных факторов наиболее надежно обнаруживать сигналы на фоне интенсивных помех и проводить оценку их временного положения с малой погрешностью [2].

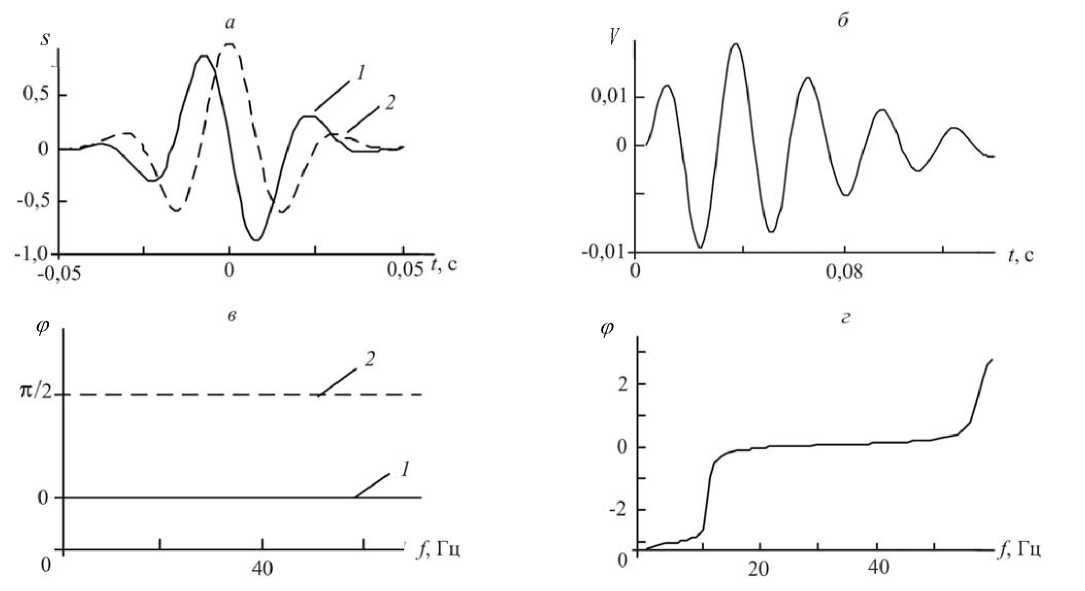
Рис. 1. Сейсмоимпульсы с колоколообразной огибающей ( а ), импульс Берлаге ( б ) и их фазовые спектры ( в , г ):

1 — нулевая начальная фаза; 2 — начальная фаза п/* 2

При определении фазовых спектров сейсмических колебаний большое значение имеет выбор на сейсмозаписи начала отсчета времени и величины временного интервала (размера окна анализа), в пределах которого выполняется преобразование Фурье. Зависимость фазовых спектров сигналов от начала отсчета проявляется в известной теореме о временном сдвиге [3]. Обычно фазовые спектры отражений имеют вид монотонных кривых без выраженных особенностей формы [4], что затрудняет выделение каких-либо закономерностей в их свойствах. Однако проведенные исследования показали, что при совмещении начала отсчета с центром окна анализа фазовые спектры наиболее часто используемых аналитических моделей сейсмоимпульсов в определенной полосе частот принимают постоянное, не зависящее от частоты значение. Эта важная особенность фазовых спектров сейсмоимпульсов названа стационарностью [5]. При ограниченной длительности сейсмоимпульсов область стационарной фазы определяется полосой частот [6]

4 f 0 0 - _Т L 0 + _Т.

где / о — преобладающая частота в спектре импульса; Т — длительность окна анализа.

На рис. 1 приведены границы области стационарной фазы, рассчитанные для импульса с колоколообразной огибающей и импульса Берлаге.

Физическое обоснование эффекта стационарности фазового спектра сейсмоимпульсов следует из известного локационного принципа передачи сигналов через линейные среды.

В соответствии с этим принципом перенос энергии сигналом возможен лишь при условии синфазности его гармонических составляющих в основном диапазоне частот. Наиболее полно этот принцип выполняется для идеально упругих сред. Для сред с поглощением наблюдается отклонение от “идеальной” стационарности. Тем не менее, как показали исследования спектров однократно отраженных сейсмических волн в различных районах Западной Сибири, и для этих сред удается выделить стационарную составляющую фазочастотной характеристики (ФЧХ). Стационарные участки выделяются и для интерференционных колебаний, обычно регистрируемых при отражении волн в тонкослоистых средах. Использование априорной информации о стационарности фазовых спектров отраженных волн и их свойствах, определяемых теоремой о временном сдвиге, позволяет синтезировать фазочастотные алгоритмы прослеживания волн с равновесной и неравновесной обработкой. Рассмотрим эти алгоритмы.

Как известно, оптимальный фазовый метод определения временного положения сигналов, наблюдаемых на фоне гауссовых помех, реализуется в виде процедуры поиска максимума функции правдоподобия следующего вида [5]:

m

L ( t ) = ^T 5 ¹ ( W k ) cos (А ф ( W k ) - W k t ) . k =1

Здесь А ф ( w k ) = ф _х ( w k ) — ф _s ( w k ) — отклонение фазового спектра сигнала от фазового спектра смеси сигнала и шума; 5 ( W k ) = A ( W k ) /ст ( W k ) — пиковое отношение сигнала к шуму на частоте ω _k ; m — число анализируемых частотных компонент.

Нетрудно показать, что в случае сильного сигнала из выражения (1) можно получить непосредственно оценку временного положения сигнала [7]

m

Е 5 ² ( W k ) W k А ф ( W k ) а _ k =1 ^T op* =      m

Е 5 ² ( W k ) W k k =1

При этом дисперсия оценки (3) равна m1

D ( T op* )= E 5 ² ( W k ) W k     .                              (4)

Тогда функцию правдоподобия (2) можно рассматривать как результат прослеживания фиксированных волн. Однако при использовании такого алгоритма возникает ряд проблем, в частности связанных с оценкой распределения отношений 5 ( W _k ) в исследуемом диапазоне частот. Как отмечено выше, форма регистрируемых с ейс мических сигналов, как правило, неизвестна, а следовательно, неизвестны 5 ( W _k ), к = 1 , m . Поэтому, учитывая, что ФЧХ сейсмических волн при определенном выборе начала отсчета окна анализа приближаются к стационарным [5], для прослеживания волн предлагается использовать так называемые фазочастотные алгоритмы с равновесной и неравновесной обработкой. Эти алгоритмы могут быть получены из оптимального фазового метода путем замены в (2) весовой функции 5 ( W _k ) на другие специально подобранные функции. В общем случае функция правдоподобия

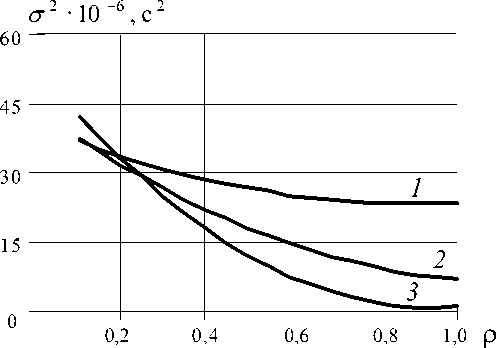
Рис. 2. Зависимость дисперсии оценки временного положения сигнала для алгоритма фазочастотного прослеживания (ФЧП) с равновесной обработкой от числа гармоник m :

1 — m = 1; 2 — m = 10; 3 — m = 20

(критерий оценки временного положения сигналов) для таких алгоритмов может быть записана в виде

m

L ( t ) = ^2 w ( W k ) cos [ ф ( W k , t )] , k =1

где w ( w k ) — частотная весовая функция, вид которой зависит от реализуемого фазочастотного алгоритма; ф ( w k ,t ) — текущий фазовый спектр участка трассы, вычисляемый в скользящем окне анализа [8].

Для равновесного алгоритма весовая функция w ( W k ) принимается равной единице во всей полосе частот [7, 9]. Для алгоритма с неравновесной обработкой w ( w k ) может иметь произвольный вид, например задана в виде функции, график которой имеет треугольную форму.

Рассмотрим сначала алгоритмы с равновесной обработкой. В случае сильного сигнала из выражения (3) получаем

т =

m

Е W k А ф ( W k ) k =1

m

Е Wk k=1

Дисперсия оценки (6) равна

^Е ' W 2 k =1 5 ² ( W k )

4     ²

(Е Wk)

Сравнение формул (4) и (7) показывает, что переход к равновесной обработке снижает точность получаемых оценок, однако такой подход требует значительно меньшее количество

априорной информации о регистрируемом сигнале, а именно только информацию о значениях его ФЧХ в анализируемой полосе частот. На рис. 2 приведена зависимость дисперсии оценок от числа анализируемых частотных гармоник. Из анализа результатов следует, что уже при m = 10 метод обеспечивает достаточно высокую точность получаемых оценок даже при отношениях сигнал/помеха, близких к единице.

Перейдем к алгоритму с неравновесной обработкой. Для этого обратимся к выражению (5) и рассмотрим случай сильного сигнала. Нетрудно показать, что в этом случае дисперсия оценки временного положения сигнала равна

D ( Т ) =

^£ W 4 ⁽ Ш к ) Ш 2 к =1    5 ² ( Ш к )

( £ W ² ( ш _ь ) Ш 2 )

Из выражения (8) следует, что точность получаемых оценок, как и при равновесной обработке, снижается, однако в данном случае она зависит также от вида функции w ( Ш к ). Как отмечено выше, в общем случае w ( Ш к ) может быть произвольной. Однако, прежде чем выбирать вид функции, проведем следующие рассуждения. Исходя из анализа (5) можно показать определенную аналогию между процедурой оценки временного положения сигналов в принятых алгоритмах прослеживания и их низкочастотной фильтрацией, а именно: выражение функции правдоподобия (2) является обратным дискретным преобразованием Фурье от результата фильтрации исходного процесса цифровым фильтром с частотной характеристикой вида [8]

H ( Ш к ) =

w ( Шк ) wr\ I

к = 1 , m,

где \Х ( к ) \ — амплитудно-частотная характеристика сигнала.

Рассмотрим влияние действия фильтра. Прежде всего отметим, что данный фильтр сначала выравнивает амплитудный спектр исследуемого колебания, а затем взвешивает его с помощью заданных весовых коэффициентов. При этом фазовые соотношения в исходной записи не изменяются. Известно, что выравнивание амплитудно-частотной характеристики при линейной фазочастотной характеристике приводит к сжатию сигнала [10], вследствие чего появляется возможность увеличить разрешение сигналов на записи. Кроме того, при реализации такого фильтра, задавая весовые коэффициенты w ( ш _к ), можно управлять его частотной характеристикой, тем самым усиливая или ослабляя различные частотные составляющие сигнала. Поэтому при дальнейших исследованиях w ( Ш к ) задавалась в виде треугольной функции [8]

w ( Ш )

<

3 ^Ш c

0 ,

2 ,

-I ^{( Ш - Ш} н ) ¹

ω c

^Ш c ^{( Ш} - ^Ш в )

ω ≤ ω _н ,

ω _н < ω ≤ ω _c ,

ω _c < ω ≤ ω _в ,

где ш в , ш _н — соответственно верхние и нижние частоты, определяющие w ( ш _к ); ш _c максимума w ( ш _к ). При этом ш c = 2 ш _н , ш в = 2 ш _с .

— частота

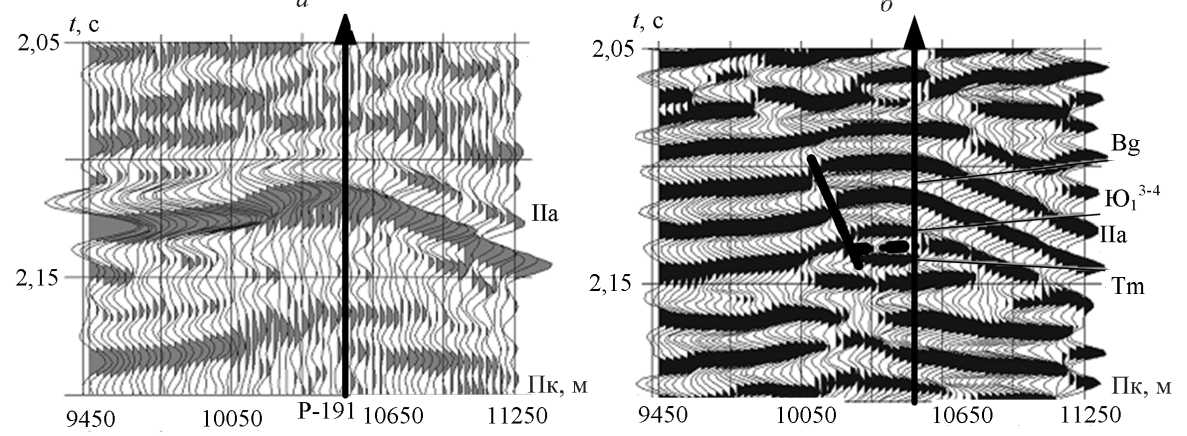
Рис. 3. Результаты прослеживания сейсмических волн:

а — разрез “общая глубинная точка”; б — разрез ФЧП; Bg — баженовская свита; Tm — тюменская свита; Ю ³ ₁ ^{- 4} — пласт верхнеюрских отложений

Исследования алгоритма ФЧП с неравновесной обработкой проводились на моделях волновых сейсмических полей и реальных данных. На рис. 3 представлены результаты прослеживания на фрагментах сейсмического разреза для одного из профилей Мыльджинского газоконденсатного месторождения Томской области. Видно, что на разрезе ФЧП (см. рис. 3, б ), в отличие от разреза “общая глубинная точка” (см. рис. 3, а ), удается выделить основные отражающие горизонты нижнего мела и верхней юры, причем четко прослеживаются даже очень слабые по интенсивности отражения. Кроме того, на разрезе ФЧП более отчетливо проявляются различные неоднородности исследуемого геологического разреза.

Таким образом, рассмотренные в работе алгоритмы фазочастотного прослеживания сейсмических сигналов с равновесной и неравновесной обработкой позволяют обеспечить высокую точность определения временного положения сигналов в условиях интенсивных помех, используя в качестве априорной информации только данные о форме ФЧХ регистрируемых волн, а также существенно увеличить разрешение сигналов на сейсмических записях, тем самым выделяя даже очень слабые по интенсивности отражения.