Алгоритмы и обработка информации в численном исследовании стохастической модели Баренблатта-Желтова-Кочиной

Уравнение Баренблатта–Желтова–Кочиной [1] с последующей редукцией к уравнению соболевского типа при различных условиях исследовалось, например, в [2, 3]. Развитие методов теории уравнений соболевского типа и теории вырожденных (полу)групп, заложенных в [4], позволило начать аналитические исследования стохастических уравнений соболевского типа и стохастической модели Баренблатта–Желтова–Кочиной [5, 6], затем были начаты разработки и численных методов для ее исследования [7].

Для исследования стохастической модели Баренблатта–Желтова–Кочиной введем в рассмот-

рение

вещественные

сепарабельные

гильбертовы

пространства

A = | u g W 2 ( D ) : — = 0 на d D | , F = W ₂ ( D ) ; ограниченную область D c R m с границей d D класса C ^w . Будем искать ц = ц ( x,t ) , удовлетворяющую в цилиндре D х[ 0, T ] , T g R , уравнению

Ldn = M^dt + Ndw,(1)

условию Дирихле

n(x,t) = 0, (x,t)g5Dх[0,T]

и условию Коши

n( x,0 ) = П0 ( x )•(3)

Здесь операторы L, M g L (U; F) такие,что L = Я-A, M = аД, параметр ^gM \ {0} , X gR характеризуют среду, а через dw обозначен обобщенный дифференциал ( U – значного, ядерного) K-винеровского процесса. Случайный процесс w w (t)=Е 4^Pk (t )^k, t g r+ k=1

называется K-винеровским процессом, где {Я} - последовательность собственных значений оператора K, занумерованных по невозрастанию с учетом их кратности. Если след оператора K TrK = ^^_Я <+^, то оператор K называется ядерным. Кроме того {вк (t)}, t eIR+ - последовательность независимых одномерных винеровских процессов.

Отметим, что исследования стохастических уравнений и стохастических уравнений соболевского типа с использованием (полу)группового подхода и методов производных в среднем ведутся отечественными и зарубежными учеными [8–13]. Кроме того, активно развиваются качественные и количественные исследования задачи восстановления динамически искаженного сигнала при наличии помех «белый шум» [14, 15].

Модель (1)–(3) описывает динамику давления жидкости, фильтрующейся в трещинноватопористой среде.

В первой части статьи приведем аналитическое решение задачи (1)–(3), во второй части приведем алгоритм ее численного решения модифицированным методом Галеркина, в третьей части приведем алгоритм численного исследования и обработки информации, получаемой в результате различных вычислительных экспериментов.

Аналитическое решение

Аналитическое исследования модели (1)–(3) приведем, следуя результатам в [16]. Прежде всего, отметим условия на параметры λ и α, которые позволяют использовать теорию относительно ограниченных операторов

Лемма 2.1. При любых Я е R \ {0} , a е R . оператор M ( L , 0 ) -ограничен.

В качестве K возьмем оператор Грина однородной задачи Дирихле Ди (x ) = 0, x edD для уравнения Пуассона -Ди = f в области D. В этом случае собственные значения {^} спектральной задачи -Дф = ЦкФк в области D имеют асимптотику цк - к2 к к ^^, в этом случае оператор Грина будет ядерным.

Следуя теории относительно ограниченных операторов и порождаемых ими вырожденных групп [4] отметим, что пространства U и F представимы в виде прямых сумм U ⁰ Ф U ¹ = U and F ⁰ Ф F ¹ = F , операторы L_k ( M_k ) есть сужение операторов L ( M ) на U^к (dom M n U^к ), к = 0,1. Если оператор M    ( L ,0 ) - ограничен, то операторы L_k е L ( U^к ; F ^к ) , к = 0 , 1 ;

M ₀ е Cl ( U ⁰; F ⁰ ) , M 1 е L ( U ¹; F ¹ ) ; существуют операторы L - ¹ е L ( F ¹; и ) и M - ¹ е L ( F ⁰; U ⁰ ) . Обозначим H = M 0"¹ L ₀ е L ( U ⁰ ) , 5 = L ^{- 1} M 1 е L ( U ¹ ) .

Пусть оператор N е L ( F ¹ ) . Тогда задача (1), (3) распадается на две независимые задачи

ШП = П ⁰ dt , П ⁰ ( 0 ) = П о ,                                (4)

d p" = S p dt + L - ¹ Ndw , П ( 0 ) = т / 0 ,                             (5)

где случайные процессы n 0 = ( I - P ) П , П = Р п , а случайные величины п 0 е L 2 ( q , U^к ) , к = 0,1, где Q - полное вероятностное пространство, P - проектор.

Уравнение в (5) имеет единственное, причем п. н. тривиальное, решение, значит, задача (4) разрешима только при нулевом значении п° , а для разрешимости задачи (1), (3) необходимо, чтобы начальное значение п0 п. н. принадлежали пространству L2 (q, U1). Обратимся к задаче (5) и перейдем к стохастическому интегро-дифференциальному уравнению tt

П = J S n dt + J L ^- Ndw .

0          0

Тогда единственным формальным решением будет случайный процесс

t n1 (t) = Un + J Ut - "L-1 Ndw (s)

или после преобразований t n1 (t) = un0 + L-1 Nw (t) + J Ut- "L-1 Nw (5) ds,                       (6)

где U ^t строится аналогично детерминированному случаю [4]:

U t = —J( p L - M ) ¹ Le ^ d p .

Y

Таким образом, справедлива

Теорема 2.1. Пусть. оператор M ( L,0-ограничен, w g L (1R₊xQ , F ¹ ) - F ¹ -значный K-винеровский процесс, оператор N g L ( F ¹ ) . Тогда для любого p ₀ g L ₂ ( q , U ¹ ) , независимых с w при каждом фиксированном t существует единственное решение задачи (1), (3) вида (6).

Алгоритм численного решения задачи Коши–Дирихле

Для численного исследования в качестве случайного воздействия будем рассматривать задачу Коши–Дирихле

p ( ^r 0 ,t ) = ⁰, |p ( ⁰, t )| <+» , p ( r ^,0 ) = P 0 ( r )                             ⁽⁷⁾

для уравнения

( Я -A r ) p_t = aA r p + w ( r , t ) ,

л d ²    1 d

.

где A r = —+ -— d r ²    r d r

Для нахождения приближенного решения будем использовать представление

N

p ( ^{r ,} t ) = p N ( ^r,t ) = X p k ( t ) ^ k ( ^r )

k = 1

где N нужно брать таким, чтобы μ_N< λ , чтобы учесть эффекты вырожденности уравнения. Если внешние возмущения случайны, то решение задачи (7), (8) будем искать потраекторно.

Прежде всего необходимо сгенерировать случайный процесс, для чего используем генератор случайных чисел, тогда

N

w(r,t) = XAk sin(tot)^k (r)

k = 1

Подставим в уравнение (8) представления для приближенного решения (9), получим NN

X(Я + Mk)pk (t)^k (r) = -aXMkpk (t)^k (r)+ w(r,t), k=1

затем умножим уравнение скалярно на собственные функции ^ _k ( r ) , k = 1,^, N. В результате получим систему N уравнений

^( 2 ⁺ Ц 1 ) ^p 1 ( t ) = ^{- a}^ 1 p 1 ( t ) ⁺<  w ( r , t ), ф 1 >

■

^ ⁽ 2 ⁺ P n ) ^p N ⁽ t ) = ^-aP N p N ⁽ t ) ⁺< w ⁽ r , t ), P n )

В зависимости от значения λ уравнения в (12) могут получаться либо дифференциальными первого порядка, либо алгебраическими.

• I.    Если Л^ст ( -А ) , то все уравнения (12) будут обыкновенными дифференциальными уравнениями первого порядка. Для решения этой системы относительно P k ( r ) , к = 1,..., N условие Коши умножаем скалярно на собственные функции ф к ( r ) , к = 1,^, N, найдем N начальных условий. Затем полученная система с найденными начальными условиями решается, таким образом, находятся коэффициенты P k ( r ) , к = 1,^, N в приближенном решении (9)

• II.    Нас больше интересует случай Л е ст ( -А ) . Предположим, что Л = ц^ = ц^ =.. . = ц _q , где

r - кратность собственных значений цq . Уравнения (12), которые соответствуют им, будут ал- гебраическими, а остальные обыкновенными дифференциальными уравнениями первого поряд- ка. Отдельно решается система алгебраических уравнений относительно p

q _j ^,

j =

1,…, r без ис-

пользования начальных условий, в результате чего получаем тривиальное решение (см п. 1) . Затем решается система оставшихся обыкновенных дифференциальных уравнений.

Алгоритм нахождения приближенного решения задачи Коши–Дирихле для стохастического уравнения Баренблатта–Желтова–Кочиной сводится к следующим этапам:

• 1.    Находятся собственные значения и собственные функции для оператора - А .

• 2.    Находится значение N из условия μ_N< λ .

• 3.    Проверка по заданному параметру λ , к какому случаю относится математическая модель – I или II. Отметим, что в случае I могут применяться различные численные методы, например [8].

• 4.    Вычисление приближенного решения при заданном начальном условии, используя метод Галеркина.

Алгоритм численного исследования и обработки информации

В основе алгоритма численного исследования стохастической модели Баренблатта–Желтова –Кочиной лежит численное решение задачи Коши–Дирихле (7), (8). Исследование стохастической модели предполагает проведение m вычислительных экспериментов, из которых в первой группе ( m ₁ эксперимент) для моделирования внешнего воздействия используется генератор нормально распределенной случайной величины с заданными параметрами математического ожидания и дисперсии, а во второй группе ( m - m 1 экспериментов) моделируется внешнее воздействие при значении случайной величины, вероятность которого крайне мала. Для первой группы экспериментов генерируются A_ki из (10), где i = 1,…, m ₁ – номер вычислительного эксперимента, для второй группы задаются A_ki из (10), где i = m 1 + 1,..., m, исходя из физический свойств случайного воздействия как редкого события. Для этого задаются математическое ожидание M ( А к. ) = 0, uD ( A ki ) = D k .

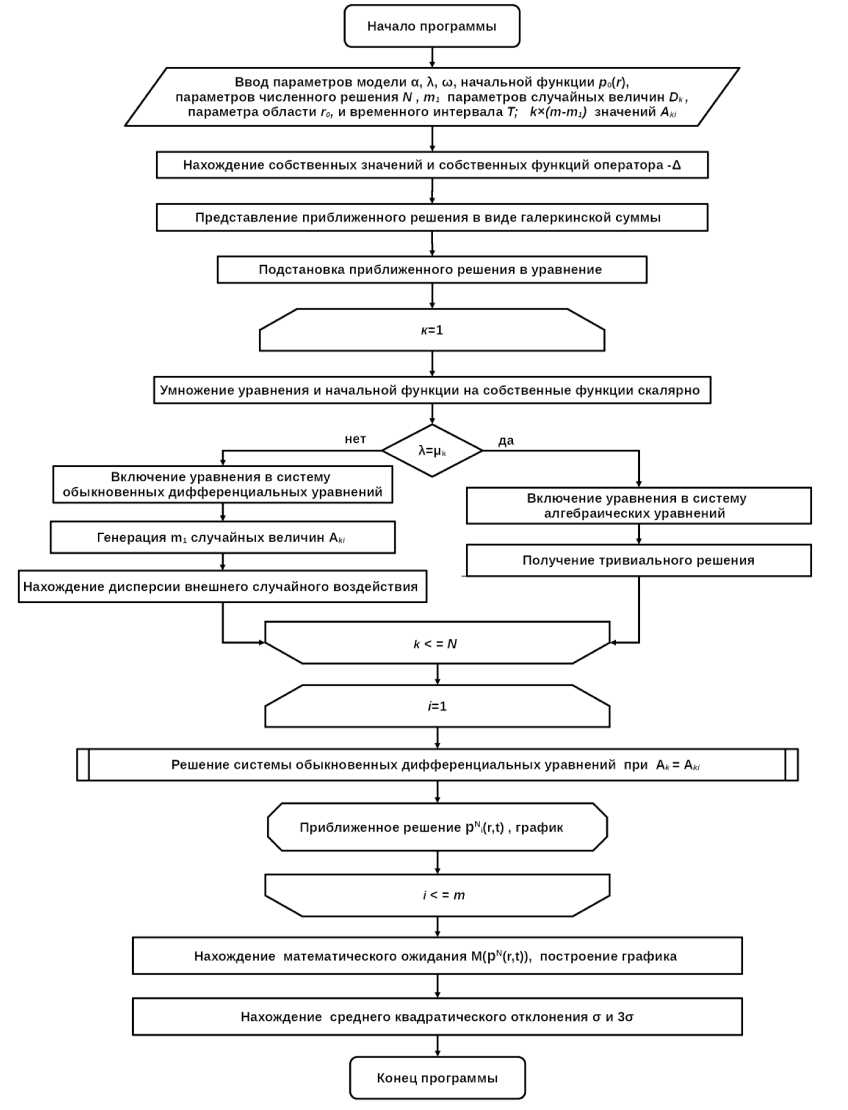
Алгоритм численного исследования стохастической модели Баренблатта–Желтова–Кочиной представлена на рисунке. После генерации случайных величин реализуются первые три этапа численного решения задачи Коши–Дирихле для стохастического уравнения Баренблатта– Желтова–Кочиной (см. п. 2). Для последующей обработки результатов запускается цикл по i , что позволяет в одной программе обработать результаты m экспериментов.

Затем идут вычисления необходимых характеристик случайных процессов. Представление случайного внешнего воздействия как (10) имеет вид канонического разложения случайного процесса. Случайные величины A_k называются коэффициентами разложения, а функции V k ( t ) = sin ( ® t ) % ( ^r ) — координатными функциями разложения. В этом случае ковариационная функция и дисперсия имеют вид

N

K ( t 1 , t 2 ) = Е D k V k ( t 1 ) V k ( t 2 ) , D ( t ) = K ( t, t ) , ⁽¹³⁾ k = 1

Кроме того, так как все А_к являются гауссовыми с математическим ожиданием m k = 0 и дисперсией D , то математическое ожидание внешнего воздействия будет равно нулю, а дисперсия определяться по (13).

к < = N

Ввод параметров модели а, Л, со, начальной функции р0(г), параметров численного решения N, mi параметров случайных величин Dk, параметра области г0, и временного интервала Т; kx(m-mi) значений Ак, к=1

Решение системы обыкновенных дифференциальных уравнений при А* = A_ki

Нахождение среднего квадратического отклонения о и За

Нахождение математического ожидания M(pN(r,t)), построение графика

Приближенное решение pNi(r,t), график

Представление приближенного решения в виде галеркинской суммы

Умножение уравнения и начальной функции на собственные функции скалярно

Нахождение собственных значений и собственных функций оператора - △

Нахождение дисперсии внешнего случайного воздействия

Включение уравнения в систему алгебраических уравнений

Включение уравнения в систему обыкновенных дифференциальных уравнений

Подстановка приближенного решения в уравнение

Генерация mi случайных величин A_ki

Получение тривиального решения

Начало программы

Конец программы

Алгоритм численного исследования стохастической модели Баренблатта–Желтова–Кочиной

Математическим ожиданием является неслучайная функция M ( p ( r,t ) ) , которая при любом значении t равна математическому ожиданию соответствующего сечения, т. е. представляет собой усредненную траекторию (реализацию), полученную в результате обработки m 1 экспериментов. Дисперсией и средним квадратическим отклонением будут являться неслучайные функции D ( p ( r, t ) ) и г т ( t ) , которые при любом значении t равны дисперсии и среднему квадратическому отклонению соответствующего сечения случайного процесса. В результате с вероятностью 0,997 || p ( r , t ) - Mp ( r , t )||< 3 a (t ).

При проведении второй группы экспериментов целью является моделирование системы, ее реакции на случайное воздействие, относящееся к редким событиям.

Варьирование параметров модели, характеризующих среду, внешнего случайного воздействия позволят на основе вычислительных экспериментов получить совокупность результатов, обработка которых методами системного анализа, позволит сделать качественные выводы о системах, моделируемых уравнением Баренблатта–Желтова–Кочиной.