Алгоритмы построения и перестроения неструктурированных четырехугольных сеток в многосвязных областях

Точность, скорость и надёжность вычислений могут быть повышены соответствующим выбором расчётной сетки. В свою очередь вид сетки зависит от числа ее узлов или ячеек, топологии, размера и формы ячеек и другого. Преимуществом использования в конечно-элементных расчётах сеток с четырехугольными и шестигранными ячейками является более высокая точность и меньшая чувствительность к эффектам сдвигового и объёмного «запирания» [1, 2]. Основные сдерживающие факторы более широкого применения такого вида ячеек связаны с недостаточным развитием автоматических алгоритмов построения сеток для многосвязных областей и закрытостью программного обеспечения для их реализации.

Существующие алгоритмы построения нерегулярных четырехугольных сеток можно разделить на две группы: прямые, в которых построение четырехугольной сетки идет без предварительной триангуляции расчетной области; непрямые, использующие предварительную триангуляцию области с последующим преобразованием треугольных ячеек в четырехугольные. В данной работе рассматривается непрямой алгоритм как более надёжный и полнее удовлетворяющий требованиям широкого круга решаемых задач (приложение к области с произвольной конфигурацией, возможность автоматического построения и перестроения сетки).

Простейший алгоритм построения четырехугольных сеток основан на методе пошагового преобразования каждой треугольной ячейки в четырехугольную путем разбиения исходного треугольника на три четырехугольника. При этом появляются новые граничные узлы, существующие граничные ребра заменяются новыми, и получаемая сетка полностью состоит из четырехугольных элементов. К недостаткам можно отнести необходимость модификации граничных ребер, а также невозможность получения четырехугольной сетки хорошего качества, соразмерной с начальной треугольной, что делает алгоритм редко применяемым в практике вычислений. Качество расчётной сетки определяется с помощью следующих мер: меры скошенности — отклонения от идеального угла ячейки q e = max [ ( a _max -a n )/ a n , ( a n -a _min)/ a _n ] , где a _min, a _max — максимальный и минимальный углы ячейки ( и = 1 для треугольной и и = 2 для четырехугольной ячеек, соответственно a 1 = 60 ° , a ₂ = 90 ° ); меры

гладкости, характеризующей изменение размеров соседних ячеек сетки и вычисляемой по формуле q_e = max _iSS_i , где S — площадь ячейки, S_i — площади соседних ячеек; мер аспектного соотношения — отношения длин максимального и минимального ребра ячейки q_e = l _max Il _min ; угловых характеристик; меры валентности и так далее. Меру скошенности 0,25…0,50 имеют сетки хорошего качества, 0,5…0,8 — сетки допустимого качества. Считается, что мера гладкости не должна превышать 30.

Алгоритм CQMesh (Convex Quadrilateral Mesh Generator) [3] использует построение так называемого «связующего дерева», каждой вершине которого соответствует треугольник начальной сетки. После построения связующего дерева начинается последовательное преобразование треугольных ячеек в четырехугольные с помощью введения дополнительных точек, которые изначально не присутствуют в сетке. Так как алгоритм не использует локальное сглаживание, в процессе его работы часто получаются сетки плохого качества, имеющие большое число ячеек с углами, близкими к 180º, и меру скошенности больше 0,95. Поэтому обязательно выполняется операция «постобработки» сетки сглаживанием, основанным на увеличении острых углов ячеек, тем самым улучшающим качество ячеек. Алгоритм CQMesh также модифицирует границу сетки; получаемая сетка полностью четырехугольная вне зависимости от каких-либо условий. Как показало тестирование, к недостаткам алгоритма можно отнести: невысокое качество сетки, определяемое исходной треугольной сеткой; в ряде случаев алгоритм может исказить границу сетки; возможны варианты, когда алгоритм добавляет точки Штейнера — точки, находящиеся за пределами разбиваемой на эмементы области.

В [4] предложен фронтальный алгоритм Q-Morph, в котором трансформация ячеек из треугольных в четырехугольные всегда начинается от так называемых ребер подвижного фронта — замкнутой совокупности ребер, отделяющей построенные четырехугольные ячейки сетки от треугольных. Далее, в процессе работы фронт постоянно обновляется в соответствии с текущим состоянием сетки. После построения четырехугольной сетки выполняется этап топологической оптимизации, то есть проводятся операции, призванные уменьшить количество нерегулярных узлов в сетке. При этом узел сетки считается регулярным, если число рёбер, сходящихся в нем, равно четырем, в других случаях — нерегулярным, а валентностью узла называется число ребер, сходящихся в узле. Отметим следующее: если начальная треугольная сетка содержит нечетное число граничных ребер, то в получаемой расчетной сетке с ячейками четырехугольной формы остается одна треугольная ячейка. Алгоритм Q-Morph позволяет получать неплохое качество сетки и не модифицировать множество граничных узлов.

Базовый алгоритм Q-Morph с рядом существенных изменений, наиболее важными из которых являются использование двух процедур построения новой ячейки и новая технология топологической оптимизации, взят за основу алгоритма QMV [5]. Алгоритм обладает теми же преимуществами и недостатками, что Q-Morph. К дополнительным преимуществам алгоритма QMV можно отнести высокую надежность метода, а также эффективные операции постобработки сетки.

• 2.    Алгоритм построения четырехугольных сеток в многосвязных областях

Предлагаемый в данной работе алгоритм QMM является дальнейшей модификацией алгоритма Q-Morph [4], которая заключается в следующем:

• – не допускается существование треугольных ячеек в конечной четырехугольной сетке;

  – объединяются методы топологической оптимизации из базового алгоритма Q-Morph и его модификации QMV;

  – реализуется построение сетки с ограничениями, то есть внутри области задаются границы, которые должны сохраниться после построения четырехугольной сетки.

Для этого ребра ограничений, например, границы разнородных   материалов,   определяются как

«защищенные». От «защищенных» ребер четырехугольная сетка строится так же, как и от граничных, то есть на начальном этапе построения они включаются во фронт перестроения. Построение четырехугольных элементов происходит в обе стороны     Рис. 1. Фронт перестроения для «защищенных» ребер в алгоритме QMM от «защищенных» ребер (Рис. 1).

Предлагаемый алгоритм QMM включает следующие шаги:

Шаг 1. Построение начальной треугольной сетки. Качество генерируемой четырехугольной сетки зависит от начальной триангуляции области. Ключевым фактором является, прежде всего, плотность узлов начальной треугольной сетки.

Шаг 2. Проверка чётности числа ребер на границе . Перед началом построения каждая замкнутая граница или граница с «защищёнными» ребрами проверяется на чётность числа ребер. При нечетном числе наибольшее из ребер контура разбивается на два новых. Исходный треугольник, содержащий разбиваемое ребро, также делится на два. В этом случае обеспечивается генерация сетки, содержащей ячейки только четырехугольной формы.

Шаг 3. Определение подвижного фронта . На начальном этапе фронт совпадает с границей области. Ссылки на ребра подвижного фронта хранятся в отдельном списке. После любых топологических операций, затрагивающих ребра подвижного фронта, список ребер подвижного фронта приводится в соответствие с текущим состоянием сетки. Алгоритм завершает работу при исчерпании списка ребер подвижного фронта.

Шаг 4. Проверка на специальные случаи закрытия фронта. В случае фронта с четырьмя или шестью ребрами используются процедуры его закрытия с формированием новых ячеек.

Шаг 5. Проверка на специальные случаи модификации фронта . Производится локальное перестроение сетки и переход на Шаг 9 .

Шаг 6. Классификация ребер фронта. Ребра фронта сортируются в соответствии с несколькими критериями; находится наиболее подходящее для построения следующей новой ячейки ребро. Этот шаг повторяется после построения каждой новой ячейки или любой топологической операции, затрагивающей ячейки, граничащие с ребрами фронта.

Шаг 7. Построение новой ячейки от ребра фронта. Для этого используются две процедуры. С помощью первой из них формируется ячейка, то есть определяются два боковых ребра и восстановливаются ребра, соединяющие узлы их верхнего основания. Вторая процедура реализуется в случае, если с помощью первой процедуры построить ячейку не удаётся. Тогда в качестве боковых ребер новой ячейки рассматриваются ребра, примыкающие к узлам активного ребра.

Шаг 8. Проверка на специальные случаи замыкания фронта. Если новая ячейка делит фронт на два или три фронтальных контура, производится проверка соблюдения условия четности количества ребер в новых фронтах. При необходимости производятся операции деления ячеек, замкнувших фронт. Ячейки делятся в соответствии с несколькими шаблонами; вид шаблона зависит от того, к каким ребрам ячейки прилегают образовавшиеся нечётные фронты.

Шаг 9. Проверка наличия ребер подвижного фронта. Если ребра подвижного фронта существуют, следует переход на Шаг 3 , в другом случае — выход из алгоритма.

Шаг 10. Восстановлениея выпуклости ячеек. По необходимости запускается блок восстановления выпуклости построенных ячеек.

Шаг 11. Топологическая оптимизация. Выполняются топологические операции, направленные на минимизацию меры нерегулярности сетки.

Шаг 12. Окончательное сглаживание. Проводится сглаживание по Лапласу всех ячеек в области.

Алгоритм QMM многократно протестирован на областях с различными видами границ и ограничений. Некоторые результаты использования предложенного алгоритма рассмотрим на примере двух многосвязных областей «A» и «Б».

Область «A» имеет одну из распространённых для тестовых примеров геометрию. При оценке и сравнении алгоритмов создания сетки для нее известны данные применения других алгоритмов. Сравненим качество сеток, построенных с помощью алгоритмов CQMesh [3] и QMM для одной и той же триангуляции многосвязной области «A». Сетки из четырехугольных элементов приведены на рисунке 2. На рисунке 2, в показана сетка, сгенерированная с помощью недавно опубликованного прямого алгоритма построения сеток с ячейками четырехугольной формы GQQMG (Garanteed-Quality All-Quadrilateral Mesh Generation with Feature Preservation) [6], который, по утверждению авторов этой работы, позволяет строить сетку с ячейками, имеющими углы в диапазоне 45º…135º. В таблице 1 приведены характеристики качества расчётной сетки «A» исходной триангуляции, а также сеток, полученных с помощью алгоритмов CQMesh, QMM и GQQMG.

Отметим, что для алгоритма QMM наблюдается незначительное увеличение числа узлов и ячеек по сравнению с CQMesh. Сгущение сетки в QMM происходит в приграничных областях. Значения максимальных углов и длин ребер элементов в обоих алгоритмах совпадают, а минимальные значения этих параметров в QMM становятся меньше. Показательной характеристикой качества сетки является параметр, определяемый через валентность ее внутренних узлов (см. последнюю строку таблицы 1, где в скобках содержится число узлов c валентностью n ). Как видно из приведенных данных, в сетке QMM большинство узлов принадлежит четырем ячейкам, то есть имеет место более регулярная сетка.

Малая величина минимального угла в алгоритме QMM возникает в результате работы процедуры восстановления выпуклости ячеек на границе области. Для достижения приемлемого максимального угла алгоритм QMM генерирует две ячейки с углами меньше 10° (Рис. 2, б , фрагмент 1 ). Как показали эксперименты, данный случай не возникает при более подробном разбиении границы начальной треугольной сеткой. Этим можно объяснить и лучшие угловые характеристики на сетке, построенной с помощью алгоритма GQQMG (см. Рис. 2, в ), поскольку и в нем генерируется значительно большее число узлов и ячеек.

Многосвязная область «Б» содержит ограничения двух видов: замкнутые (включение и полость) и открытые (две линии) (см. фронты перестроения на Рис. 3, а ). В общем случае для задачи построения расчётной сетки с ограничениями задаётся множество ребер, которые становятся ребрами сетки. Потребность в такой сетке возникает при геометрическом моделировании различных поверхностей: трещин, разломов, границ водоёмов, разного рода рельефов и так далее. Также ограничения необходимы при построении сеток с возможностью задания различного типа граничных условий, в том числе условий симметрии.

Таблица 1. Сравнение характеристик работы алгоритмов CQMesh, QMM, GQQMG

Характеристика	Исходная треугольная сетка	Сетка CQMesh	Сетка QMM	Сетка GQQMG	Сетка QMM после перестроения ячеек с граничными ребрами
Число узлов	1341	1510	1857	32789	7884
Число ячеек	2160	1249	1594	30321	7085
Максимальная длина ребра, см	50,6	46,9	46,6	-	46,6
Минимальная длина ребра, см	1,81	1,81	0,54	-	0,06
Максимальный угол, град	118,7	169,9	169,8	≈ 135	162
Минимальный угол, град	15,0	15,0	7,5	≈ 43	15,7
Валентность узла (число таких узлов)	4 (6),       5 (203), 6 (348),    7 (202), 8 (47),     9 (3)	3 (317),    4 (420), 5 (198),    6 (41), 7 (1),        8 (1)	3 (147), 4 (1043), 5 (132)	-	3 (608),    4 (5082), 5 (569),   6 (17)

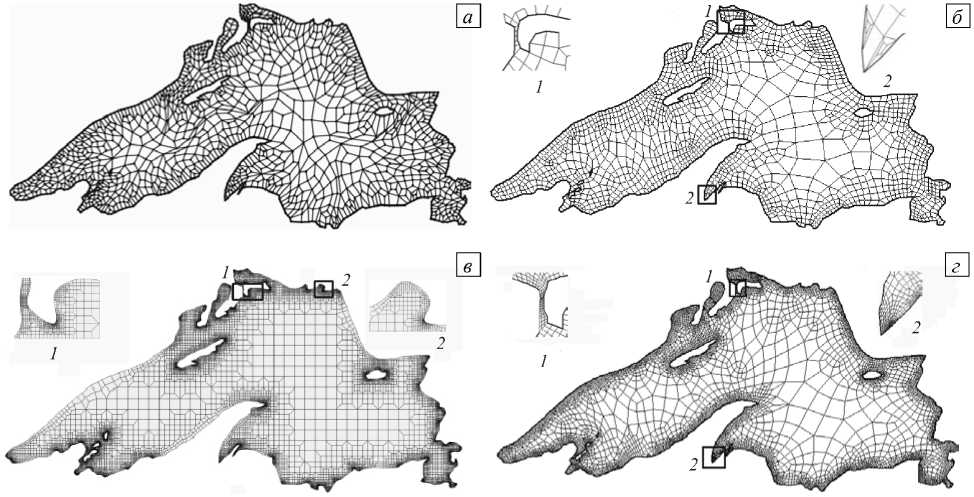
Рис. 2. Область «A».

Сетки, полученные с помощью разных алгоритмов: CQMesh (а), QMM (б), GQQMG (в), QMM с перестроением ячеек по границе (г)

Отметим, что алгоритмы QMV и GQQMG не обрабатывают открытые и замкнутые «защищенные» ребра, а алгоритм CQMesh — только открытые. По сравнению с начальной треугольной сеткой «Б» генерированная сетка четырехугольных элементов имеет существенно меньшее число узлов и элементов. Характеристики, определяющие качество расчетных сеток «Б» исходной триангуляции и сеток, полученных с применением алгоритма QMM, приведены в таблице 2. Результаты показывают, что для генерации высококачественной сетки с ограничениями требуется перестроение получаемых четырехугольных ячеек в локальных областях ограничений.

Отметим, что перестроение сетки дает возможность встраивать ограничения в сетку, свободную от «защищенных ребер». Кроме того, при решении задач с помощью метода конечных элементов часто возникает необходимость уточнения полученного решения на выбранной подобласти или во всей области. Это достигается также благодаря алгоритмам перестроения начальной расчётной сетки (треугольной или четырехугольной).

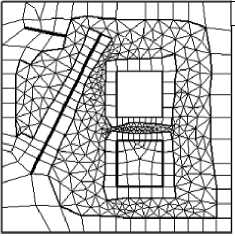
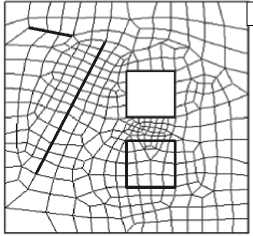
Рис. 3. Область «Б». Фронты перестроения в алгоритме QMM ( a ) и перестроенная с его помощью сетка четырехугольных элементов со структурными ребрами ( б )

• 3.    Алгоритм перестроения неструктурированных четырехугольных сеток

В данном разделе рассматривается перестроение только четырехугольной сетки. Предложена новая модификация подхода Шнейдера для применения к неструктурированным сеткам, генерируемым алгоритмом QMM в комбинации с операциями его топологической оптимизации.

Необходимым условием возможности модификации является конформность сетки (согласованность узлов в соседних ячейках) и сохранение выпуклости ячеек после перестроения. Также важно, чтобы экстремальные величины углов в ячейках при трансформировании сетки сохраняли постоянство. В отличие от алгоритмов перестроения треугольных сеток [7, 8], где используется всего два основных варианта (или шаблона) перестроения (бисекция — деление на два треугольника по «большой» стороне или «новому» узлу, и регулярное — на четыре треугольника), для четырехугольников известно несколько схем перестроения, удовлетворяющих указанным требованиям. Базовыми можно считать две из них [9], в которых выбранный четырехугольник разбивается, соответственно, на четыре или девять новых четырехугольников. Предположим, что ячейки, выбранные для адаптации, образуют множество помеченных четырехугольников, а ячейки, которые необходимо перестроить для согласования,— множество согласующего перестроения.

Выбор алгоритма перестроения на девять ячеек связан с тем, что в этом случае угловые характеристики сетки не зависят от уровня адаптации выбранной области, то есть алгоритм обладает устойчивостью. Так, при первом перестроении помеченного четырехугольника полученные углы сохраняются при всех последующих преобразованиях данной ячейки. Для неструктурированной сетки особое внимание необходимо уделять выбору точек внутри изменяемых ячеек и обеспечению согласованного перехода между выбранными для перестроения ячейками и остальным множеством четырехугольников.

Рассмотрим варианты шаблонов перестроения помеченных и согласующих ячеек с гарантируемым сохранением выпуклости вновь образованных ячеек.

Шаблон перестроения помеченных ячеек . На рисунке 4, а представлен стандартный шаблон разбиения ячейки, помеченной для перестроения, при использовании метода Шнейдера. Все узлы, лежащие на ребрах четырехугольника, разбивают исходные рёбра на три равные части.

Шаблон согласующего перестроения 1. Этот вид шаблона используется в случае, если ячейка имеет одну общую с помеченным для перестроения четырехугольником вершину A (Рис. 4, б ). Тогда в качестве новой внутренней точки E выбирается точка пересечения прямых ME и EN, при этом ME П DC и EN П CB . В этом случае четырехугольник ANEM подобен четырехугольнику ABCD , а значит, является выпуклым. Четырехугольники MECD , NECB выпуклы как трапеции.

Шаблон согласующего перестроения 2. В случае двух общих вершин A , B возможны варианты перестроения, приведенные на рисунках 4, в , г . Если ячейка имеет три общие вершины A , B , C с перестроенными четырехугольниками, то согласующее перестроение выполняется, как показано на рисунке 4, д.

В работе использовался модифицированный алгоритм перестроения Шнейдера, в котором, в отличие от базового алгоритма, понятие уровня перестроения ребер и узлов не играет роли (в классическом варианте от этого зависит вычисление уровня перестроения четырехугольника). Тогда предлагаемый алгоритм можно представить следующим образом:

Шаг 1. Определение области перестроения. На этом шаге задается соответствующий уровень перестроения каждой ячейки n . Все ячейки с уровнем больше единицы далее будут разделены на 3 ⁿ и более частей.

Шаг 2. Формирование списка ячеек для перестроения. В список ячеек для перестроения включаются все четырехугольники с уровнем перестроения больше единицы, а также все соседние ячейки.

Шаг 3. Определение помеченных узлов. Каждый узел, принадлежащий хотя бы одной ячейке с n >  1 считается «помеченным». По числу «помеченных» узлов четырехугольника выбирается шаблон его перестроения.

Шаг 4. Перестроение выбранных ячеек. Разбиваются все ячейки из списка перестроения. Уровень перестроения вновь образованных ячеек устанавливается следующим образом: если n — начальный уровень перестроения ячейки, тогда n - 1 — уровень перестроения ячеек, образованных при ее разбиении.

Шаг 5. Проверка уровня перестроения вновь образованных ячеек. Для ячеек с уровнем перестроения больше единицы осуществляется переход на Шаг 2.

Шаг 6. Окончательное сглаживание. Выполняется сглаживание ячеек в области перестроения.

За перестроением сетки следует топологическая оптимизация для уменьшения появившихся нерегулярных узлов. Топологическая оптимизация алгоритма QMM, кроме базовых операций («вставка узла», «удаление узла» и так далее), использует шаблоны шестирёберных контуров (см. контуры C 6 в [9]). На заключительном этапе перестроения выполняется окончательное сглаживание сетки.

На рисунке 5, а представлена сетка для области «Б» после одного перестроения всех четырехугольников, содержащих защищенные и граничные ребра. Рисунок 5, б демонстрирует случай перестроения всех ячеек сетки «Б», а рисунок 2, г — сетку для области «А» после перестроения ячеек на границе. Некоторые величины, характеризующие качество построенных для области «Б» сеток, приведены в таблице 2. Как видно из таблицы, в сетке «Б» минимальные углы стали несколько меньше, а

максимальный угол унаследовался от исходной перестраиваемой сетки. В других тестовых примерах, где максимальный угол не столь большой, качество сохранялось и после перестроения области.

На рисунке 2, в приведен пример использования модифицированного алгоритма перестроения Шнейдера в комбинации с алгоритмом QMM и операциями его топологической оптимизации для сетки «А» с уточнением описания границы области. Полученные характеристики сетки после перестроения границы содержит таблица 1. Отметим, что при уточнении границы увеличивается минимальный угол, однако степень детализации описания границы всё ещё остается недостаточной в сравнении с алгоритмом GQQMG.

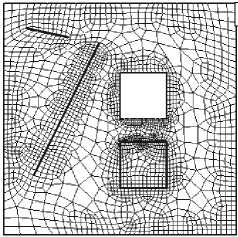
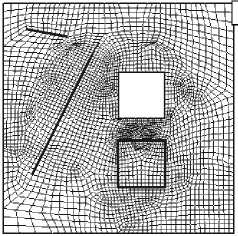
Рис. 5. Сетка «Б» после перестроения четырехугольников с «защищенными» ребрами ( а ) и после перестроения всех ячеек ( б )

Таблица 2. Характеристики сеток для области «Б» до и после перестроений

Характеристика	Треугольная сетка «Б»	Четырехугольная сетка «Б»	Сетка «Б» после перестроения ячеек с «защищенными» ребрами	Сетка «Б» после перестроения всех ячеек
Число узлов	507	397	2122	3357
Число ячеек	942	361	2014	3249
Максимальная длина ребра, мкм	64,4	64,4	26,1	21,5
Минимальная длина ребра, мкм	4,52	2,44	0,89	0,81
Максимальный угол, град	131,4	177,1	176,3	177,1
Минимальный угол, град	22,0	28,5	18,2	12,8
Валентность узла (число таких узлов)	4(17),        5(112), 6(190),       7(101), 8(14)        9(1)	3(38),        4(255), 5(31)        6(1)	3(108),       4(1698), 5(97)        6(3)	3(38),       4(3071), 5(31)        6(1)

4. Заключение

Предложенный алгоритм автоматического построения и перестроения неструктурированных четырехугольных сеток позволяет существенно повысить точность вычислений и упростить задание различного рода ограничений и граничных условий при моделировании. На рисунках 6, 7 представлены некоторые результаты, полученные с его использованием. Проведено моделирование структуры и осуществлен расчёт механического поведения сплава с 20%-ным содержанием кремния конечноэлементным методом на сетке из четырехугольных элементов с линейной аппроксимацией перемещений. Расчётная сетка содержала 56896 ячеек и 57054 узлов, аспектное отношение равнялось 26, максимальный угол составлял 162°, а минимальный — 18°. Модель микроструктуры достаточно точно аппроксимирует морфологию микрошлифа, а сравнение результатов, вычисленных по конечно-элементной модели и установленных в эксперименте, показывает хорошее совпадение полей напряжений и деформаций, главных напряжений и других механических характеристик.

Программная реализация разработанного алгоритма QMM выполнена на основе общей структуры данных среды расчетных сеточных моделей для параллельных вычислений FEStudio [10], позволяющей

Рис. 6. Структура материала: реальная ( а ) - микрошлиф (205 х 180км

) материала Al-Si-Mg с включениями Si, и

расчётная ( б ) – перестроенная сетка модельной области, содержащей 97 включений

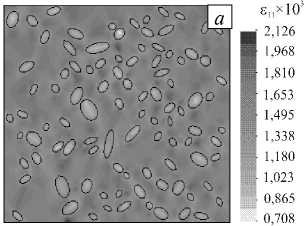
Рис. 7. Поля интенсивности деформаций (а) и главных напряжений (MПа) (б), рассчитанные конечно-элементным методом на сетке, представленной на рисунке 5, б

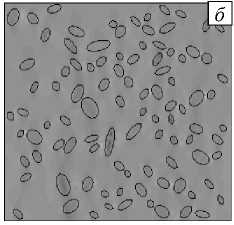
273,920 248,930

223,940 198,950 173,960 148,980 123,990

99,000 74,012

49,026

работать с CAD-геометрий (с файлами DXF формата), что существенно расширяет возможности данного комплекса по построению расчётных сеток из четырехугольных конечных элементов и генерации трехмерных дискретных областей путем отображения двумерных сеток с ячейками четырехугольной формы.

Работа выполнена в рамках программы Президиума РАН № 18 при финансовой поддержке УрО РАН (проект 12-П-1-1034) и РФФИ (проект № 11-01-00275-а).