Алгоритмы теории графов в модели международной торговли

Постановка задачи. Рассмотрим n стран-участниц торговли с государственными бюджетами x ₁ , x ₂ ,..., x_n . Рассматривая госбюджет каждой страны, имеем в виду ту его часть, которая тратится на закупку товаров внутри страны или на импорт из других стран в течение некоторого временного периода. Пусть А – структурная матрица торговли, ее элементы a_ij – часть госбюджета, которую j -я страна тратит на закупки товаров i -й страны. Матрица А и вектор госбюджетов связаны матричным уравнением. Определим, каким условиям должна удовлетворять данная неотрицательная матрица, чтобы существовал положительный вектор x , т.е. существовало такое соотношение между торговыми бюджетами стран-участниц, которое бы обеспечивало сбалансированность международной торговли (бездефицитность торгового бюджета).

Структурная матрица торговли A = ( a j ) , где a j - доля импорта из страны i в бюджет страны j , - обладает некоторыми свойствами: она неотрицательная ( A >  0 ), квадратная, и сумма элементов в каждом ее столбце равна 1.

Пусть структурная матрица торговли имеет вид:

all a12    . a ..    a1 n A= a 21 ... a22    . ...      . ..a2n .. ... . an 1 an2    . ..   ann) и пусть x = (x1,x2,...,xn)T - вектор бюджетов стран-участниц торговли.

Тогда при подведении итогов торговли за некоторый временной период (например, за год) i -я страна имеет выручку p i = a i 1 x 1 + a i2 x 2 + ... + a in x n , i = 1,2,..., n . Чтобы торговля была сбалансированной, необходимо потребовать бездефицитность торговли для каждой страны: p i >  x i , i = 1,2,..., n . Можно доказать [3], что условием бездефицитной торговли являются равенства: p i = x i , i = 1,2,..., n .

Пусть p i >  x_i , тогда для всех i = 1,2,..., n имеем:

a 11 x 1 + a ₁₂ x ₂ + ... + a 1 _nx_n >  x 1 ;

a ₂₁ x 1 + a ₂₂ x ₂ + ... + a _{2 n}x_n >  x ₂;

a n 1 x 1 ⁺ a n 2 x 2 ⁺ ... ⁺ a nn x n >  x n .

Суммируя неравенства (1), получаем:

( a 11 + a ₂₁ + ... + a n 1 ) x 1 + ( a ₁₂ + a ₂₂ + ... + a n ₂) x ₂ + ... + ( a 1 _n + a _{2 n} + ... + a_nn ) x_n >  x 1 + x ₂ + ... + x_n . (2)

В левой части выражения (2) все суммы в скобках, как суммы элементов столбцов матрицы А , равны 1. Тогда получаем противоречивое неравенство:

x ₁ + x ₂ + ... + x_n >  x ₁ + x ₂ + ... + x_n .

Следовательно, предположение о том, что p i >  x i не верно, т.е.

P i = x i ,     i = 1,2,..., n ,                                               (3)

или выручка должна равняться бюджету, чтобы торговля была сбалансированной.

В матричной форме полученную систему уравнений (3) можно представить в виде

Ax = x .                                           (4)

Тогда x - собственный вектор матрицы А , принадлежащий собственному значению 1. Существование такого собственного вектора вытекает из следующей теоремы [3].

ТЕОРЕМА. Если в матрице А сумма элементов каждого столбца равна единице, то существует собственный вектор, принадлежащий собственному значению 1.

Докажем, что 1 является максимальным собственным значением неотрицательной матрицы А . Используем для этого теорему Фробениуса – Перрона [3, 5], нередко применяемую для исследования линейных экономических моделей.

ТЕОРЕМА Фробениуса – Перрона. Пусть А – неотрицательная квадратная матрица ( A >  0 ) и X A - максимальное по модулю собственное значение матрицы А (число Фробениуса). Тогда справедливы следующие утверждения:

• 1.    X A - действительное неотрицательное число. Существует неотрицательный собственный вектор x A , соответствующий данному собственному значению (вектор Фробениуса).

• 2.    Если A >  0 , то X A >  0 , и существует положительный собственный вектор матрицы А , определенный однозначно с точностью до умножения на положительное число.

Теперь, докажем, что 1 является числом Фробениуса матрицы А [3].

Пусть е = (1,1,..., 1) ^T - n -мерный единичный вектор. Так как в матрице А все суммы по столбцам равны 1, то A T e = е . Пусть X A - число Фробениуса, тогда найдется такой неотрицательный ненулевой вектор у , что Ay = X A y .

Рассмотрим скалярное произведение е и Ay :

е T • Ay = е ^T -XAy =X A ( е ^T • у) ,                                 (5)

е T • A^y = ^{( a} 11 y 1 + ^a 12 y 2 + ... + a 1 п У п ) + ^{( a} 21 y 1 + ^a 22 y 2 ^{+ ... +} a 2 п У п ) ⁺ ".

• ^{+    (} a n 1 ^y 1 ⁺ a n 2 ^y 2 ⁺ ... ⁺ a nn y n ) = ^{( a} 11 ⁺ a 21 ⁺ ... ⁺ a n 1 ) ^y 1 ^{+ ( a} 12 ⁺ a 22 ⁺ ... ⁺ a n 2 ) y 2 ⁺ ...

^{+ ( a} 1 n ^{+ a} 2 n ⁺ ... ⁺ a nn ) У п = A^T"e ^{- y} = e T • ^y.                             ⁽⁶⁾

Так как е T • у = у 1 + у ₂ + ... + y_n >  0 , то из уравнений (5), (6) получаем:

X

A

^*

e

T

^*

• у

^*

e

T

^*

• у

= 1 .

Таким образом, 1 – максимальное собственное значение матрицы А . По теореме Фробениуса - Перрона существует неотрицательный вектор X A , соответствующий данному собственному значению, т.е. уравнение AX = X имеет ненулевое неотрицательное решение X .

Так как бюджет любой страны xi > 0, то интерес представляет только положительное решение X > 0. Для A > 0 существование положительного решения следует из теоремы

Фробениуса – Перрона. Но в более общем случае, если какая-то j -я страна не импортирует товары из страны i (aij = 0), то матрица А не является положительной (A > 0). Возникает вопрос о существовании положительного решения уравнения (4) в случае, когда матрица А неотрицательна.

Представим структурную матрицу А как матрицу весов взвешенного ориентированного графа, в котором каждой вершине поставлена в соответствие страна-участница международной торговли. Доля госбюджета aij ставится в соответствие дуге (i, j) орграфа. Если aij = 0, то дуга из вершины i в вершину j отсутствует. Ненулевым диагональным элементам матрицы aii , т.е. долям госбюджета, затраченным на закупку товаров внутри страны, соответствуют петли графа.

Докажем теорему, которая дает ответ на поставленный раннее вопрос.

ТЕОРЕМА 1. Если, в модели международной торговли, структурную матрицу A >  0 представить как матрицу весов орграфа, в котором вершинам соответствуют страны-участницы торговли, и если данный орграф является сильно связным, то уравнение AX = X имеет единственное положительное решение X >  0 с точностью до умножения на положительное число.

Доказательство. Так как орграф сильно связный, то для любых двух вершин орграфа i и j ( i * j ) существует ( i , j ) -маршрут и ( j , i ) -маршрут.

Согласно известному из теории графов утверждению [4], в графе с n вершинами ( i , j ) -маршрут ( i * j ) существует тогда и только тогда, когда ( i, j ) -й элемент матрицы A + A ² + ... + A " ¹ не равен нулю.

Следовательно, учитывая, что матрица A >  0 , имеем:

(A + A2 +... + A"-1)j > 0, т.е. в матрице A + A2 +... + A"1 вне главной диагонали все элементы положительны.

Сложив эту матрицу с единичной E , получим положительную матрицу:

B = E + A + A ² + ... + A " ^{- 1} >  0 .

Пусть X - собственный вектор матрицы А , соответствующий собственному значению X . Тогда

BX = ( E + A + A ² + ... + A " ^{- 1}) X = X + X X + X ² X + ... + X " ^{- 1} X = (1 + X + X ² + ... + X " ^{- 1}) X .

Таким образом, вектор X одновременно является и собственным вектором матрицы B .

Доказано, что 1 является числом Фробениуса матрицы А , следовательно, уравнение AX = X имеет неотрицательное решение X. Всякое такое решение X > 0 является и собственным вектором матрицы B. Но так как матрица B положительна, то, по теореме Фробениуса – Перрона, собственный вектор матрицы B, соответствующий числу Фробениуса, положителен и определен однозначно с точностью до умножения на положительное число, т.е. X > 0. Следовательно, уравнение AX = X имеет положительное решение X, единственное с точностью до умножения на положительное число. Теорема доказана.

Далее приведем пример расчета соотношения между торговыми бюджетами шести стран-участниц, для которых структурная матрица торговли имеет вид:

	' 0,290	0,159	0,000	0,000	0,186	0,000 ^
	0,307	0,174	0,257	0,000	0,307	0,316
	0,169	0,000	0,273	0,278	0,254	0,000
A =	0,204	0,350	0,227	0,393	0,253	0,306	.                                  (7)
	0,030	0,050	0,000	0,329	0,000	0,378
	ч 0,000	0,267	0,243	0,000	0,000	0,000 ;

Так как матрица A >  0 , то, используя теорему 1, выясним, существует ли положительное решение уравнения AX = X .

Для этого торговые связи между странами представим в графическом виде (рис.1). Чтобы не загромождать рисунок, веса дуг (доли госбюджетов) на данном орграфе не обозначены.

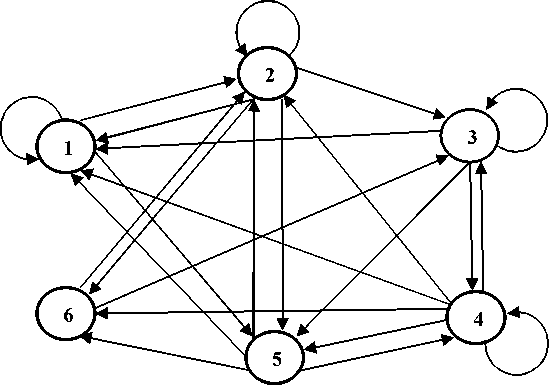
Рис.1. Ориентированный граф, соответствующий структурной матрице А

Рассматривая сильную связность орграфа, условимся петли, если они есть, не брать во внимание.

Для того, чтобы проверить, является ли орграф сильно связным, был реализован алгоритм выделения сильно связных компонент орграфа, использующий поиск в глубину, который применяется в самом графе и в траспонированном [1, 2]. Разработано программное средство в среде Turbo Pascal 7.0, входными данными в котором является орграф с n вершинами, представленный массивом ребер, а выходными данными – количество сильно связных компонент орграфа и массив номеров соответствующих компонент.

С помощью данной программы установлено, что орграф, соответствующий примеру модели обмена (рис.1), является сильно связным, и все его вершины принадлежат одной сильно связанной компоненте.

Следовательно, по теореме 1 уравнение AX = X имеет положительное решение. Для нахождения этого решения воспользуемся математической системой MathCAD.

На рис.2 приведен пример расчета соотношения между торговыми бюджетами 6 стран-участниц для матрицы (7), обеспечивающего сбалансированность торговой модели. Ответ дается в нормализованном виде.

	' 0.290	0.159	0.000	0.000	0.186	0.000'
	0.307	0.174	0.257	0.000	0.307	0.316
	0.169	0.000	0.273	0.278	0.254	0.000
A : =
	0.204	0.350	0.227	0.393	0.253	0.306	r : = rows ( A )
								i : = 1... r
	0.030	0.050	0.000	0.329	0.000	0.378
	0.000	0.267	0.243	0.000	0.000	0.000,	r = 6	S i-^ A

S^T = ( 1 1 1 1 1 1 ) - суммы элементов матрицы А по столбцам

X : = eigenvals ( A ) - вычисление собственных значений матрицы А

Х ^т = ( 1 - 0.132 + 0.146 i - 0.132 - 0.146 i 0.254 0.07 + 0.247 i 0.07 - 0.247 i )

x : = eigenvec ( A ,1 ) - вычисление собственного вектора матрицы А для X =1

x^T = ( 0.176 0.4 0.421 0.691 0.332 0.209 ) - вектор соотношений торговых бюджетов

(A■ x)т =(0.176 0.4 0.421 0.691 0.332 0.209) - проверка m := min(x)    m = 0,176     x1 := —

m x1T =(1 2.266 2.387 3.916 1.880 1.185) - нормализованный вектор

Рис.2. Расчет в системе MathCAD соотношений торговых бюджетов 6 стран-участниц

Таким образом, сбалансированность торговли данных стран (торговой модели) может быть достигнута только в том случае, когда их государственные бюджеты находятся в соотношении 1 : 2,266 : 2,387 : 3,916 : 1,880 : 1,185.

Выводы. Модель международной торговли представлена в удобном и наглядном графическом виде.

С применением теории графов сформулирована и доказана теорема, позволяющая определить существование и единственность точного сбалансированного решения для общего случая неотрицательной структурной матрицы торговли. Разработана программа, использующая алгоритмы теории графов и позволяющая для каждого конкретного примера проверить существование такого решения. С помощью компьютерного пакета MathCAD рассчитано искомое соотношение между торговыми бюджетами стран-участниц.