Алгоритмы вычисления собственных значений дискретных полуограниченных операторов, заданных на квантовых графах

Введение. В статьях [1-18] разработан численный метод нахождения собственных значений дискретного полуограниченного дифференциального оператора вида L = T + P , заданного в сепарабельном гильбертовом пространстве H с областью определения D L е H . Здесь T -самосопряженный оператор такого же порядка, как и оператор L . Рассмотрим краевую задачу, порожденную оператором L :

Lu = y u , Gu | _г =0,                                  (1)

где Г - граница области D L . Для нахождения собственных значений { y n } ” ₌₁ спектральной задачи (1) произведем дискретизацию области D L и построим последовательность { H n } ” =1 конечномерных пространств, которая полна в H . Подберем ортонормированные базисы { p k } k =1 пространств H n с H таким образом, чтобы они удовлетворяли граничным условиям задачи (1).

В статье [16] доказана теорема.

Теорема. Приближенные собственные значения y n спектральной задачи (1) находятся по линейным формулам

Кадченко С.И., Ставцева А.В., Рязанова Л.С., Дубровский В.В.

К ( ⁿ ) = ( L 9 n , Фп ) + § n , n ^e N ,                                 ⁽²⁾

~    n - 1

где S _n = X [ ^Hk ^{( n -} 1 ) - ц _к ( n ) ] , p k ( n ) - n -е приближения по Галеркину к соответствующим к = 1

собственным значением р _к спектральной задачи. При этом lim S _n = 0.

n ^W

За систему координатных функций  {фк }к=1  возьмем систему собственных функций спектральной задачи

Tv = A v , Gv | _г =0.                                       (3)

С учетом собственных значений { Д }^i и ортонормированных собственных функций

{ v_k } _k =1 оператора T формулы (2) записываются в виде

H n ( ⁿ ) = ^An + ( Pv n , v' n ) + 5 _n , ^{n e} N •                              ⁽⁴⁾

Линейные формулы (4) позволяют находить приближенные собственные значения с необходимым порядковым номером, зная спектральные характеристики соответствующего невозмущенного оператора. Они позволяют находить собственные значения оператора независимо от собственных значений с меньшими порядковыми номерами. Решают проблему вычисления всех точек спектра дискретного полуограниченного оператора lj = 1 с любыми порядковыми номерами. С возрастанием порядкового номера собственного значения оператора

В5 = — n   bn

(40 + 28cos(6 4аП ) + 52cos(4 . Д ’) + 75cos(2 ^Д ) + 9cos(8 М))

точность его вычисления

по формулам (4) возрастает.

В данной статье рассмотрены вопросы нахождения приближенных собственных значений на квантовых графах с использованием формулы (4).

• 2.    Прямые спектральные задачи на квантовых графах . Пусть G = G ( V , E ) - конечный

связанный ориентированный граф с последовательно соединенными ребрами. Через V = { Vt }*°_ обозначено множество вершин графа G, а через E = {E}J0  - множество его ребер. Каждое

^{1 J} ; j = 1

ребро E j графа G имеет длину l j > 0 и площадь поперечного сечения d j > 0 . На каждом ребре

E _j графа G задан дискретный полуограниченный вектор-оператор

L = (L1,L2,-",LJ0 ), действующий в гильбертовом пространстве

H = L2 (G) = {G = (G1,G2,...,Gj0), Gj eL2[0,lj], j = 1,70} со скалярным произведением j0

( g , h ) = X d j J g j h j ds,   g ’ h ^{e H} .

J=10

Для компанент вектор-оператора L = T + P рассмотрим спектральные задачи (TJ + PJ)uj = Huj, uj = uj (sj), j = 1, j0

^U J ( ⁰ ) = u k ( ⁰ ) = u m ( ^l m ) = u n ( ^l n ) = ⁰,

У d_jd^Uj

E ₇ e E ^a ( V i )     ^ds j

dum

У, a m ds s7 =0  Em e Em( V)

= 0, l _m

d 2 u;2

где T j U j = - —J ; P j U j = X p j_k ( S j )u ^2" ^k ) ; U j , p j e ( Г / |0, l j ]; k=1,2; S j e [0, l j ].

dsJк

Граничные условия (8) означают, что вектор-функция u = (и1,и2,...,Uj^) непрерывна во внутренних вершинах графа G , а условие (9) - что поток через каждую вершину графа G равен нулю. В формулах (9) через Ea®) (Vi) обозначены множества дуг с началом (концом) в вершинах V, а Ej, Ek е Ea (V ) , Em, E e E® (V).

Найдем собственные значения и собственные вектор-функции для вектор-оператора T = ( T 1 ,T 2 ,...,T j^ ) . Для этого рассмотрим на графе G следующие спектральные задачи:

Tjvj = Avj , vj = vj (sj), j = 1jo ,

Vj( 0 ) = Vk ( 0 ) = Vm (lm ) = Vn (ln ) = 0,(11)

Z  d/dj   - Z d.^vm    = 0.(12)

E j e E ^a ( V i )     ds j s j = 0    E m e ^E ® ( V i )     ds m S m = l m

Собственные значения { A n } n =1 спектральной задачи (10)-(12) занумеруем в порядке неубывания их величин. Как правило, система собственных вектор-функций { v _п = ( V n , v ₂ n ,—, V jn )} w =i задачи (10)-(12) ортогональная и ее легко сделать нормированной.

Если она не ортогональная, то ее необходимо разложить в ряды Фурье по системе вектор-функций ^{ Ф п =⁽_< Ф_Х11Ф 2.n ,... j^)} j =1 ^и нормализовать.

Нахождение собственных значений A и соответствующих им собственных вектор-функций v _n = ( V _п , v_2п ,•••, V jn ) спектральных задач (10)-(12) для любых конечных замкнутых графов с большим количеством вершин приводит к большому количеству и громоздкости аналитических вычислений. Для упрощения этого процесса в среде математического пакета MAPLE был написан пакет программ, позволяющий находить необходимое количество этих спектральных характеристик для любых конечных графов [18].

На основании формул (4) и (6) следует, что приближенные собственные значения вектор-оператора L, действующего в сепарабельном гильбертовом пространстве W2(G), находятся по формулам j^                         --1А

Мп ( п ) = An +Z dj Xj (s )J vjn ( s )Z Pjk (s )vjn   (s) ds + 5n ,  n e N .

j = 1            0          k = 1

Здесь x j ( s ) =

<

'1, s e [0, l j ],

0, S ^ [0, l j ].

Таким образом, по формуле (13) можно вычислять приближенные

собственные значения прямой спектральной задачи (10)-(12), если заданы на ребрах графа G все функции P jk .

• 3.    Численные эксперименты. Проверку разработанной методики вычисления собственных значений дискретных полуограниченных операторов заданных на геометрических графах проведем на примере молекул ароматических соединений антрацена C ₁₄ H₁₀ . Граф,

моделирующий молекулу антрацена, состоит из четырнадцати вершин ( i₀ =14) и шестнадцати ребер ( j ₀=16) (см. рисунок). Нахождение собственных значений A n и соответствующих им собственных вектор-фунций v _п оператора T при решении спектральных задач (10)-(12) для конечных замкнутых графов с большим количеством вершин вызывает большие аналитические трудности. Поэтому в среде аналитических вычислений MAPLE был написан пакет программ, позволяющих находить эти спектральные характеристики для любых конечных орентированных графов [18].

Кадченко С.И., Ставцева А.В., Рязанова Л.С., Дубровский В.В.

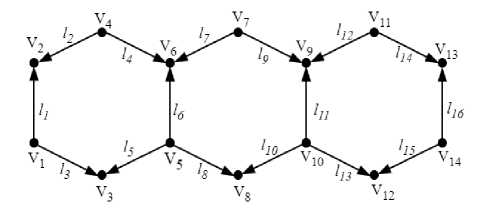
Разбиение ориентированного графа, моделирующего молекулу антроцена на вершины и ребра

Так как длины всех ребер для молекулы антрацена одинаковы, можно считать, что lj = 1 и dj = 1 для всех j = 1, j0 . Используя написанный пакет программ, получили трансцендентное уравнение для нахождения собственных значений I спектральной задачи (10)-(12) 62sin( VI) + 190sin(3 VI) + 384sin(5 VI) + 463sin(7 VI) +

+ 415 sin(9 V I ) + 225 sin(11 V I ) + 81sin(13 V I ) = 0.

Компоненты vj собственных вектор-функций vn спектральной задачи (10)–(12), которые соответствуют собственным значениям I, записываются в виде vjn = In [ j sin (^s ) + 4 cos (^s )] ,                    (15)

где

A = — (8sin( 4i ) + 23sin(3 4i ) + 16sinI) + 9sin(741)), n _an

B₄ = -4(58 + 88cos(2 41 ) + 49cos(4 41 ) + 9cos(6 41 )), b _n

A ₂ =—(26sin( ,ДГ) + 61sin(3 4I ) + 48sin(5 41 ) + 21sin(7 4I )), ⁿ    a _n

B2n =  (16 + 30cos(2^ ) + 15 cos(44!) + 7 cos(6Ц)), bn

A 3 = - ±(8sin(^) + 23sin(3 ДТ_п ) + 16sin(5 41 ) + 9sin(7. Д Т)), n      _an

B3 = — (58 + 88cos(2 ^) + 49cos(4 ^) + 9cos(6 ^)), n   bn                   n                 nn

A ₄ = - —(26sin( JI ) + 61sin(3 41 ) + 48sin(5 J^ ) + 21sin(7 ^I )), ⁿ

B4 =12(16 + 30cos(2 JI) +15 cos(44I) + 7 cos(6^)), n   bn                    n                nn

A 5 = — (41sin( T I T) + 85sin(3 ^^ ) + 80sin(5 ^^ ) + 37sin(7 ^^ ) + 9sin(9 ^I )), ⁿ a_n

B  = -1 (40 + 28 cos(6 VI) + 52 cos(4 Л) + 75 cos(2 ^) + 9 cos(8 .JI)), n   bn                    n                n                nn

A ₆ = — (5sin( JI ) + 9sin(3 41 ) + 16sin(5 41 ) + 13sin(7 41 ) + 9sin(9 41 )), n _{a n}

B 6„ = Г (40 + 28 cos(6 41 ) + 52 cos(4 41 ) + 75 cos(2 41 ) + 9 cos(8 41 )), b_n

A7 = —(93sin(^Xn ) + 212sin(3^Xn ) + 214sin(5JX,) + 124sin(7^Xn ) + 45sin(9^Xn )), n   an

B4 = — (64 + 99 cos(2 X) +127 cos(4 a/X) + 73 cos(6 a/X) +15 cos(8 a/X)), n   bn                     n                   n                  nn

A8 = -— (23sin( ^Xn) + 47sin(3 ,л.) + 48sin(5 7!) + 25sin(7 7!) + 9sin(9 a/X)), na

B8 = — (40 + 75 cos(27X) + 52 cos(4 7X) + 28 cos(6 ^) + 9 cos(8 JX)), n   bn                    n                n                 nn

A = - — (93sin( J! ) + 212sin(3 J^ n ) + 214sin(5 J^ n ) + 124sin(7 JX ) + 45sin(9 J! )),

n

B9 = — (64 + 99cos(2JX) + 127cos(4 7X) + 73cos(6 7X) + 45 cos(8 7X)), n   bn                    n                  n                nn

A ₁₀ = — (217sin( JX ) + 127sin(3 JX ) + 234sin(5 JX n ) + 185sin(7 7 X ) + 87sin(9 JX )), ⁿa

B10 = — (29 + 84 cos(2JX) + 101cos(47X) +107 cos(6JX ) + 60 cos(8 TX + 27 cos(10JX))), n   bn                     n                   n                   n                  nn

A 11 = - —(8sin( a/ X ) + sin(3 JX n ) - 30sin(5 ^) - 63sin(7 ^|X n ) - 30sin() - 51sin(9 JX )), ⁿa

Bn = — (29 + 84cos(2 7X) + 101cos(4 7X) + 107cos(6 JX) + 60cos(8 7X + 27cos(10 7X))), n   bn                   n                 n                  n                nn

A12 = — (103sin( JX) + 291sin(3 J!) + 392sin(5 JX) + 371sin(7 Л) + n an

+ 261sin(9 JX ) + 81sin(11 Jx )),

B2 = —(5 + 45cos(2 JX) + 60cos(4 7X) + 84cos(6 .JX) + 51cos(8 ^ + 27cos(10 ^))), n   bn                  n                n                n                nn

A ₁₃ = - —(34sin( 4X ) + 108sin(3 ^/ X n ) + 132sin(5 J X n ) + 124sin(7 ^X ) + n

+ 69sin(9 .ДГ) + 27sin(11 ^)),

B13 = — (29 + 84cos(2 ^X) + 101cos(4 ^X) + 107cos(6 ^) + 60cos(8 ^X + 27cos(10 ^))), n   bn                   n                 n                  n                nn

A ₁₄ = - —(103sin( 4X ) + 291sin(3 .JX ) + 392sin(5 ^X ) + 371sin(7 ^X ) + ⁿa

+ 216sin(9 4X ) + 81sin(11 ,JX )),

BM = —(5 + 45cos(24X) + 60cos(44X) + 84cos(6 ^X) + 51cos(8 .JX + 27cos(104X))), n   bn                  n                n                n                nn

A ₁₅ = — (105sin( ^X ) + 266sin(3 .JX ) + 482sin(5 ^X ) + 523sin(7 .JX ) + ⁿ   a_n

+ 442sin(9 jXn ) + 225sin(11 Jin )), В _15и =1,

A16 = — (19sin( JXn) +114sin(3 JX) + 286sin(5 JX) + 403sin(7 JX) + n   an

+388sin(9jXnn) + 225sin(11 jXnn) + 81sin(13JXX)), Bi6„ =1, an = 43sin( д/Д) + 154sin(3 Д/) + 320sin(54Д) + 403sin(7 д/Д) + +388 sin(9 д/Д) + 225sin(11 Д/) + 81sin(13 Д/, bn =16 +11sin(2 Д/) + 143sin(4 Д/) + 177sin(6 ДД) + 244sin(8 Д/) + +144sin(10 Д/) + 81sin(12 Д/).

Система {vn}”  ортогональна в смысле скалярного произведения (6). Множители Cj , п1                                                                                                                          jn входящие в (15), находятся из условия нормировки этой системы.

В табл. 1, 2 приведены результаты вычисления первых собственных значений вектор-оператора L, заданного на графе, который моделирует молекулу антрацена. Расчеты были проведены для следующих заданных функций p j ( s j ) (1 <  j <  16, k = 1,2 , s j e [0, l j ]): k

P j =^{0, 1} <  j <  ^16, P 1₂ = s ^{2 + 5,} P 2₂ = s ^{2 + 5} s ⁺ 1, P 3₂ = s ^{2 + 5} s - 1, p 4₂ = ⁵ s ⁺ 1, P 5₂ = ⁵ s - 1,

P 6₂ = ^0, P 7₂ =5 ^{s +} 1, P 8₂ = ⁵ s ^- 1, P 9₂ = s ^{2 + 5} s ⁺ 1, P 10₂ = s ^{2 + 5 s -} 1,

P 11₂ = s ^{2 + 5} s , P 12₂ = s ^{2 + 5} s ⁺ 1, P 13₂ = s ^{2 + 5} s - 1, P 14₂ =⁵ s ⁺ 1, P 15₂ =5 s - 1, P 16₂ =¹⁵ s 2 - ⁹

Таблица 1                                       Таблица 2

п	рп	А п	1 цп - Ап 1
1	1,941823	- 0,233790	2,175613
2	2,341721	2,639681	0,297960
3	2,985317	3,237994	0,252677
4	3,399854	3,402611	0,002757
5	3,735492	4,079347	0,343855
6	4,433908	4,615242	0,181334
7	5,174741	5,566181	0,391440
8	9,639011	9,777037	0,138026
9	12,046596	11,989504	0,057100
10	14,999971	15,078706	0,078740
11	22,637372	22,584269	0,053100
12	26,389451	26,283345	0,106110
13	28,364816	28,264205	0,100610
14	28,927379	29,020026	0,092650
15	30,917058	30,892965	0,024090
16	31,675799	31,728728	0,052930
17	36,423006	36,537131	0,114120
18	41,600790	41,681763	0,080970
19	47,346396	47,400335	0,053940
20	60,803221	60,734402	0,068820

п	А	А п	1 рп - Ап 1
32	133,782235	133,836558	0,054400
33	138,087581	138,073378	0,014200
34	139,363870	139,410644	0,046700
35	149,351679	149,400349	0,048600
36	160,022389	160,057500	0,035100
37	171,268499	171,293752	0,025300
38	196,385492	196,337380	0,048100
39	207,948995	207,929674	0,019300
40	213,591153	213,560590	0,030600
41	215,799666	215,842331	0,042600
42	221,265569	221,252390	0,013200
43	222,830313	222,882445	0,052100
44	235,432590	235,485607	0,053000
45	248,847190	248,889225	0,042000
46	262,838151	262,872782	0,034600
47	293,789481	293,775166	0,014300
48	307,937209	307,962172	0,025000
49	314,826087	314,833452	0,007400
50	317,553092	317,621732	0,068600
51	324,179804	324,204533	0,024700

В табл. 1, 2 под ц _п обозначены собственные значения спектральной задачи (7)-(9), которые вычислены по формулам (13), а ц _п - вычисленные методом Галеркина с использованием скалярного произведения (6).

• 4.    Заключение. Использование написанного в математической среде MAPLE пакета программ для нахождения собственных значений Д _п и соответствующих им собственных вектор-фунций v _п оператора T , при решении прямых спектральных задач (10)-(12), заданных на конечных ориентированных графах, значительно упрощает нахождение собственных значений вектор-оператора L по формулам (13).

Проведенные многочисленные вычислительные эксперименты по вычислению собственных значений оператора L , заданного на графе G , показали высокую вычислительную эффективность разработанной методики.