Альтернансный метод в векторных задачах параметрической оптимизации систем с распределёнными параметрами

В ряде актуальных для приложений ситуаций возникают трактуемые с позиций системного подхода новые, существенно отличающиеся от традиционных постановки задач оптимального управления (ЗОУ) системами с распределёнными параметрами (СРП) в усложнённых условиях векторной формы предъявляемых требований к критериям эффективности, учитываемым ограничениям и выбору управляющих воздействий. Трудности отыскания алгоритмов оптимизации в векторной задаче оптимального управления (ВЗОУ) значительно возрастают по сравнению с их известными скалярными частными случаями. В настоящей работе предлагаются конструктивные методы решения подобных ВЗОУ СРП применительно к типичным для приложений оценкам в равномерной метрике точности приближения конечных состояний СРП к требуемым.

Развиваемый подход базируется на процедуре предварительной параметризации искомых управляющих воздействий с помощью известных условий оптимальности и последующей редукции исходной задачи к специальным модификациям задачи математического программирования с бесконечным числом ограничений (задача полубесконечной оптимизации -ЗПО), разрешаемым альтернансным методом, являющимся развитием теории нелинейных чебышёвских приближений применительно к рассматриваемому кругу ЗПО [1, 2].

1 Модели и методы многокритериальной оптимизации СРП

Оценка эффективности функционирования сложных управляемых систем как правило производится в приложениях по различным показателям качества, чаще всего конфликтующих друг с другом, что приводит к задаче выбора возможных альтернатив для управляющих воздействий в условиях неопределённости целей процесса управления (многокритериальная задача управления - МЗУ). Отбор приемлемых вариантов производится при этом среди эффективных решений (множество Парето), не улучшаемых ни по одному из критериев без ухудшения показателей по какому-либо из остальных.

Традиционные способы редукции исходной МЗУ к однокритериальной свёртке компонентов векторной целевой функции с заданными весовыми коэффициентами приводят к построению множества Парето путём перебора всех допустимых значений таких коэффициентов, вследствие чего возникает самостоятельная проблема оптимального выбора в пределах этого множества единственной альтернативы в условиях значительного числа возможных вариантов [3-6].

Переход путём соответствующей процедуры нормирования к относительным равнозначным оценкам всех составляющих векторного критерия с последующим использованием их минимаксной (или максиминной) свёртки с единичными весовыми коэффициентами позволяет непосредственно получить парето-эффективное решение многокритериальной задачи, которая в итоге сводится после параметризации искомых управляющих воздействий к специальной задаче математического программирования (ЗМП) с учётом всех изначально заданных ограничений [4, 5].

Применительно к СРП формулируемая в итоге ЗМП принципиально усложняется и принимает вид ЗПО с бесконечным числом ограничений в типичных условиях их оценки в равномерной метрике [1, 2].

Для СРП с управляемой функцией состояния Q ( X , t ) , описываемой в пределах односвязной т -мерной пространственной области V э X , 1 <  m <  3, с кусочно-гладкой границей S линейным неоднородным уравнением в частных производных параболического типа с типовыми краевыми условиями и внутренними u_V ( t ) или граничными u_S ( t ) сосредоточенными управляющими воздействиями, МЗУ формулируется в следующем виде:

I _х ^ min ;

u ∈ Ω_Σ

I х = ⁽ I p ⁽ u )) , p = 1, q ; u ^{G {} u v ⁽ t ) , u s ⁽ t ^)} ; Q_z = { u : ^ф х ⁽ u ) <  8^ u G ^[ u min , u max i } ;

Ф_х ( u ) = max Q ( X , t ) - Q .

X ∈ V

Здесь I p ( и ) - частные критерии оптимальности, заданные в типовой форме интегральных функционалов качества, общее число которых равно q >  1; s ₀ - заданная точность равномерного приближения состояния Q ( X , t * ) СРП в конечный момент времени t = t * к требуемому Q ** ( X ) = Q ** = const , и Q ( X , t ) представляется в форме разложения в сходящийся в среднем ряд по собственным функциям ф n (X ) начально-краевой задачи модели СРП ∞

Q ( X , t ) = ^ Q n ( t ) ф _п ( X ) с коэффициентами (временными модами) Q n ( t ) , поведение кото- n = 1

рых моделируется бесконечной системой обыкновенных дифференциальных уравнений, фигурирующей в качестве модального описания СРП в предлагаемых далее процедурах решения МЗУ [7].

Переход от I p к относительным равнозначным оценкам X _p ( и ) приводит к минимаксной свертке МЗУ (1) [4]: *

• (2)        X ( и ) = max X ( и ) ^ min ; X ( и ) = -p^ ;0 <Х ( и ) <  1, p = 1, q ,

pe{1,q} p        иеп^      p         1"p -1p точка оптимума которой и* заведомо принадлежит множеству Парето исходной МЗУ и может рассматриваться в качестве искомого решения задачи (1) [4]. Здесь I*р и Ip - минимальная и «наихудшая» величины I p соответственно в условиях заданных ограничений.

Минимаксная задача (2) эквивалентна обычной однокритериальной задаче t *                                       7^0                                  **

• (3)    I = If X ⁰ dt = Л" ^ min ; — = 0; X p ( и ) = z^{p (} t )". ^Ip <  X ⁰ , d p = f , p ( Q , и ) ; p = U.

t 0               и еПБ   dt       p        Ip -1p с интегральным функционалом качества (4), ограничениями на величину Xp (и), минимизируемым параметром X0 = const, модальным описанием СРП и дополнительными переменными zp(u), p = 1 ,q , вводимыми наряду с Q = (Qn), n = 1,2,..., где f0p (Q,и) - подынтегральные функции критериев Ip (и ).

Распространяемая на такую задачу стандартная процедура принципа максимума Понтрягина, как правило, позволяет найти и *( t ) в форме явной зависимости и ** ( Q *( t ), Т * ( t )) от соответствующих оптимальному процессу векторов Q * и Т * модальных составляющих Q ( X , t ) и сопряжённых переменных Т ( t ) независимо от ограничений на Q ( X , t *) и z_p ( t *) в (1) и (3) [2].                                                 _____

Полученные указанным образом зависимости и ( Q , Т ) во многих случаях непосредственно устанавливают структуру искомых оптимальных алгоритмов и * ( t ) в форме их параметрического описания с точностью до вектора А ( N ) = ( A ^{( N} ) ), i = 1, N , упорядоченной последовательности конечного числа N параметров A ^{( N} ) , А 2 ⁾ ,..., A N ) , непосредственно характеризующих поведение управления и *( t ) в области его определения [1, 2].

Интегрирование уравнений объекта с параметризованным управлением и(А(N), t) приводит в таких случаях к представлению Ip, Xp и конечного состояния Q(X, t*) в виде явных достаточно гладких зависимостей, соответственно, Ip(А(N)), Xp(А(N)) и Q(X, А(N)) отА(N), если считать известными значения I *р и Ip в (2).

Размерность N вектора А ⁽ N ) устанавливается по известным правилам в зависимости от значения s ₀ в (1), либо априори фиксируется возможностями технической реализации А ^{( N} ) -параметризуемых управляющих воздействий [1, 2].

В результате производится точная редукция задачи (3) к ЗПО

(4)	I = Я 0 ( A ( N ) ) ^ min ; A ( N )

(5)             Ф, ( А ^{( N} ’ ) = max Q ( X , А ^{( N} ’ ) - Q “I <  £ ,

X e V

^{( N} )      *               ___

• (6)                 X p ( A ^{( N} ) ) = I^{p ( А} 0 ) * I p <  Я ⁰ , p = 1 , q

IP - Ip на минимум целевой функции (4) конечного числа N переменных Ain), i = 1, N, с бесконечным числом ограничений на величину Q(X, А(N)) для всех X e V, которая отличается от её стандартной формулировки в задачах с одним критерием оптимальности [1,2] дополнительными ограничениями (6) на величину Xp.

Рассматривая вместо (4) критерий оптимальности

I„ = X ( А ⁽ N ) ) ^ min ^{p      p} 1^v      ’     _A( N )

последовательно для всех p 1 = 1, q , получим ряд ЗПО (5), (7), рассмотренного в [1, 2] типового вида, на решениях которых А ^{( N} ) = А ^{[ p 1 ]} , определяемых по схеме альтернансного метода, вычисляются X _p ( А ^{[ p 1 ]} ) V p = 1, q . За решение А ^{( N} ) исходной задачи (4)-(6) принимается А ^{[ p 1]}

*

Г *1                       Г *1

X _p ( А ^{[ p 1]} ) p * * ( А ^{[ p 1]} ) для всех

при таких p 1 = p 1 , для которых выполняются неравенства

• p = 1, q .

Это решение обладает альтернансными свойствами [1, 2], порождающими замкнутую относительно всех искомых параметров оптимального процесса систему равенств (8) в некоторых R точках X о e V .

I Q ( X 0 , A ^{( N} ) ) - Q “I = £ 0 ,       Q ( X ° , A ^{( N} ) ) = 0; X °, e int V , j = 1, R ; v = 1, R 1 ; R 1 < R ;

d X

N , £ 0 >  min s ( A ^{( N} ) ) ;

R =^

N + 1, £ 0 = min £ ( A ^{( N} ) ) ;

min £ ( A ⁽ N ) ) = min maxi Q ( X , A ⁽ N ) ) - Q “I .

A ⁽ N ) L X eV ¹                      U

При наличии дополнительной информации из предметной области о конфигурации зависимостей Q(X, A(N)) на V э X, позволяющей идентифицировать значения X0 и знаки разностей Q(Xj1, А(N)) - Q**, соотношения (8) трансформируются к системе R + R1 уравнений относительно R + Ri неизвестных значений A(N),i = 1, N; min£(A(N)), если £0 = min£(A(N)) и координат X0v, v = 1, R1, точек XOv е{X0 }, решение которой находится известными численными методами и исчерпывает решение исходной задачи МЗУ.

На этом этапе принципиальную роль играют нестандартные процедуры использования в целях получения указанной информации фундаментальных физических характеристик конкретных оптимизируемых процессов, предварительное исследование которых представляет собой отдельную достаточно сложную задачу.

Величины I p в (2) находятся решением по схеме альтернансного метода частных однокритериальных задач оптимизации с заданными ограничениями вида (1) на точность £ ₀p приближения Q_p ( X , t *) к Q “ в условиях £ ₀ <  £ _0p , p = 1, q .

Значения I p могут быть формально определены решениями «обратных» задач на max I_p или установлены, исходя из физических соображений.

По найденному указанным способом вектору Д ⁽ N ) и известным зависимостям A _p ( Д ⁽ N ) ) вычисляется минимальное значение A in целевой функции в (4)

О             О ( N )       О    ⁽ N )                  ⁽ N )

• ⁽⁹⁾               A nin = min ^{A ( Д}   ) = ^{A ( Д} ) = ^max ^ п ^{( Д}   ),

Д ⁽ N )                                     p e { 1 , q } p

«автоматически» обеспечивая тем самым выполнение требований к A _p ( Д ⁽ N ) ) в (4).

Исходная ЗПО значительно упрощается как раз в наиболее характерной для приложений ситуации с минимально достижимой величиной £ ₀ = min £ ( A ( N ) ) в классе Д ⁽ N ) - параметризуемых управлений и сводится в таком случае к задаче достижения этой величины без дополнительных ограничений [1, 2].

Самостоятельный интерес представляют МЗУ СРП в характерных условиях интервальной неопределённости начальных состояний и неизменных во времени параметрических характеристик объекта управления [8]. Подобные МЗУ сводятся по описанной схеме к разрешаемой альтернансным методом ЗПО, отличающейся от детерминированного варианта, во-первых, оценкой точности £ о равномерного приближения конечного состояния СРП к требуемому на расширенном множестве аргументов, включающем кроме пространственных переменных все возможные реализации неопределённых факторов, и, во-вторых, определением частных критериев оптимальности в форме функций максимума на допустимом множестве изменения учитываемых неопределённых величин.

2 Параметрическая оптимизация СРП в задачахс комбинированными требованиями к конечным состояниям объекта

Наряду с ЗОУ, рассматриваемыми в обычных условиях единственного требования к Ф_Е ( и ) вида (1), значительный теоретический и практический интерес представляет их расширенная постановка с одновременно предъявляемыми различными ограничениями на оцениваемые в равномерной метрике конечные состояния объекта, отличающимися друг от друга формами их функционального представления F ( Q ( X , t * )) , видами эталонных распределений по пространственным координатам Q“(X ) и допустимой точностью £ _к приближения Q ( X , t * ) к Q~( X ):

• ⁽¹⁰⁾              Ф^ ( и ) = maxi F ( Q ( X , t *)) - Q ** ( X )| <  £ , k = 1 , w ; w >  1 .

X ∈ V

Подобные ЗОУ СРП возникают, в частности, применительно к техническим объектам с распределёнными параметрами, функционирующим в составе технологических комплексов, взаимосвязи между элементами которых диктуют необходимость перехода к векторному варианту (10).

Так, например, в ЗОУ температурными режимами предварительного нагрева металлических полуфабрикатов в технологических комплексах обработки давлением [9-11] вместе с требованиями к точности равномерного приближения Q ( X , t * ) к Q ** в (1) во многих случаях следует с позиций системного подхода учитывать ограничение на ошибку отклонения Q ( X , t *) от желаемого стационарного состояния объекта [12] на возможном этапе термостатирования перед передачей обрабатываемых изделий к деформирующему оборудованию или(и) дополнительное ограничение на погрешность приближения средней на каждом элементе пространственной области температуры к её заданной величине, обеспечивающей минимальное энергопотребление на стадии пластического формоизменения [9, 10].

В однокритериальном варианте с q = 1 в (1) ЗОУ СРП с комбинированными ограничениями (10) редуцируется после параметризации искомых управлений подобно (4), (5) к ЗПО следующего вида

• (11)             I (А * ^N > Ц m i n;

• (12)              Ф, ( а * ⁿ ' ) = maxi F„QX , А * ^N ' ) ) - Q* ** (X )| < s ; k = L w,w > 1 ,

X eV где w требований (12) непосредственно сводятся к единственной оценке дискретной функции максимума по составляющим Фk в (9), нормируемых с учётом отличающихся значений sk.

Дальнейший переход к одному эквивалентному ограничению в типовой форме оценки непрерывной функции максимума базового варианта альтернансного метода обеспечивается линейной свёрткой всех компонентов дискретной функции максимума с ограниченной суммой весовых коэффициентов, играющих роль искомых переменных в соответствующей задаче линейного программирования (ЗЛП) на максимум этой свёртки. В итоге ЗОУ СРП с комбинированными ограничениями приводится к типовому виду ЗПО со специальной формой единственного ограничения на точность s0 равномерного приближения результирующего состояния объекта к требуемому, рассматриваемого на расширенном множестве аргументов, в число которых наряду с пространственными координатами входят искомые переменные ЗЛП w a = (ak ) e Aw, k = 1, w, изменяющиеся в пределах типового симплекса Aw = {ak > 0, ^ ak = 1} k=1

и заведомо являющиеся координатами вершин многогранника допустимых решений ЗЛП:

• (13)       I ( а ^{( n 1} ) ^ mi™ ; Ф 0 ( А ^{( N} ) ) = max ^T a_t S ⁰-| F _t ( q ( X , А ^N ) ) ) - Q * ( X ) < s ₀,

где в качестве s ₀ может быть выбрана любая величина s_n , ne { 1, w } . Здесь y = ( x , a ), X e V , V 1 = V x A w , a_k = 1, j = 1, w 1 и заведомо при некоторых k = k j e {1, w } получаем a_k = 1, j = 1, w 1 ; 1 <  w 1 <  w , где w 1 >  1 - число активных ограничений в (12).

Конструктивный вычислительный алгоритм решения задачи (13) по схеме альтернансно-го метода, усложняемый необходимостью предварительного выделения w 1 активных ограничений из общего их числа w в (12), приведён в [13].

3    Метод параметрической оптимизации в задачахмногоканального управления системами с распределёнными параметрами

Целый ряд актуальных для приложений ЗОУ СРП формулируется в условиях одновременного воздействия на объект по различным каналам управления [14-16].

Самостоятельный достаточно общий класс задач подобного типа возникает для о >  1 взаимосвязанных СРП [16-25] с использованием управляющих воздействий U ( t )

U ⁽ t ) ё ^{ u m ⁽ t ) ^: u m ⁽ t ) ^{ё {} u Vm ⁽ t ), u Sm ⁽ t ^)}; u m min — u m ⁽ t ) — u m max ;

UVm (t) = (UVm1 X1 = 1 Vm; ; uSm (t) = (uSml X1 = 1 lSm i m = X^ ° > 1} в виде совокупности различных для каждого т-го объекта (m е{1,о}) векторных сосредоточенных внутренних uVm (t) или граничных uSm (t) управляющих воздействий с фиксированным характером их пространственного распределения, где для простоты исключается случай их совместного применения. Частный случай о> 1 в (14) соответствует задаче векторного управления одним объектом.

С помощью аналитических условий оптимальности может быть получено подобно предыдущим задачам параметрическое представление каждой 1 -ой компоненты искомых управлений u_m ( t ) в (14) с точностью до однозначно характеризующего управляющие воздействия   u_m ( t )  оптимальной структуры вектора   A ⁽ l^m ) = ( A ⁽ m ^}), I = 1, 1_m ; 1_m e {l_Vm , 1_Sm };

k = 1, N1m , определённым образом упорядоченной последовательности конечного числа N1m σ lm параметров А^), общее количество которых равно N = ∑∑ N 1m .

m = 1 I = 1

В итоге, аналогично (11), (12) осуществляется редукция исходной ЗОУ к ЗПО следующего вида:

• ⁽¹⁵⁾            I ^{( А} ) ^ min ; max Q m ⁽ X m , ^А ) ^- Qm⁽ X m ) ^— S m , ^m = ^о,

ΔΣ   Xm∈Vm m m        m m     m где А1 = (A(lm)), m = 1, о; I = 1,1m и £m- заданная точность равномерного приближения конечного состояния т-ой управляемой величины Qm (Xm, А) к требуемому Qm*(Xm) в пространственной области Vm изменения пространственных координат X m т-го объекта в системе взаимосвязанных СРП.

Решение задачи (15) может быть получено по схеме альтернансного метода, однако технология его применения существенно усложняется по сравнению с одноканальным управлением увеличенной размерностью вектора Δ^Σ , многовариантным набором правил выбора чисел N_1m в этих условиях; специфическим требованием одинаковой длительности процесса управления для всех компонентов управляющих воздействий, ограничивающим свободу их независимого друг от друга выбора, и необходимостью идентификации конфигураций оптимальных конечных пространственных распределений каждой из управляемых величин в условиях их зависимости от всех внешних воздействий.

4    Оптимальное управление объектом технологической теплофизики

В качестве примера, представляющего самостоятельный интерес, рассмотрим задачу оптимального по быстродействию управления температурными режимами индукционного нагрева металлических заготовок перед последующей обработкой давлением с описанием температурного поля Q(x, t) нагреваемой заготовки цилиндрической формы в зависимости от радиальной координаты х и времени t линейным одномерным неоднородным уравнением теплопроводности в относительных единицах с классическими краевыми условиями третьего рода и внутренним сосредоточенным управляющим воздействием по мощности электромагнитных источников тепла при заданных допустимых пределах её изменения [11].

К результирующему температурному состоянию Q ( x , t ), достигаемому в конечный момент t процесса нагрева, одновременно предъявляются два требования вида (10): равномерного нагрева до заданной температуры Q = const с допустимой погрешностью е 1 при к = 1, F 1 ( Q ( x , t * )) = Q ( x , t * ) в (10) и обеспечения допустимой точности е 2 равномерного приближения средней величины Q _c ( x , t * ) разности Q ( x , t * ) - Q* * к нулю на любом отрезке [0, x], x <  1, вдоль радиуса цилиндра при k = 2,

I F 2 ^{( Q ( x} , t *)) ^{- Q} “ | = Qc ^{( x} , t *)| = ^T j [ Q ( n , t* ) ^{- Q} “ \ddn ^x 0

в (10), исходя из типичных требований к средней температуре деформируемого изделия на всём протяжении последующих операций его пластического формоизменения [9, 10].

Процедура принципа максимума Понтрягина обеспечивает параметризованное представление оптимального по быстродействию управляющего воздействия с точностью до вектора A ⁽ N ) = ( A (N ) ), i = 1, N , конечного числа N параметров A ⁽ N ) , A ⁽ N ) ,..., A ⁽ N ) , в роли которых фигурируют длительности интервалов постоянства искомых управлений релейной формы, попеременно принимающих на отрезке [0, t * ] э t только свои априори фиксируемые предельно допустимые значения [2]. Интегрирование уравнений объекта с параметризованным указанным образом управлением позволяет получить конечное распределение температур и значение критерия оптимальности I = t * в форме явных достаточно гладких зависимостей Q ( x , A N ) ), I ( А ⁽ N ) ) от своих аргументов.

В результате производится точная редукция исходной задачи оптимального быстродействия к ЗПО вида (11), (12) на минимум функции I ( А ⁽ N ) ) конечного числа переменных A^ ) , i = L N :

N

• (17)           I ( A ^N > ) = ^N ⁾ ^ m N n , —

с бесконечным числом ограничений, диктуемых требованиями вида (12) для всех x е [0,1] :

Ф1 ( A ⁽ N ) ) = max Q ( x , A ⁽ N ) ) - Q ** <  е ; x e [ 0 , 1 ] ।                                   ।

(19)              Ф 2 ( A ( N ) ) = max x e [ 0 , 1 ]

x — j[ Q ( n , A ( N ) ) - Q * n dn <  е 2 x 0

Здесь критерий оптимальности I в (17), равный продолжительности процесса нагрева, представляется простой суммой длительностей A ⁽ iN ) интервалов постоянства оптимального управления и * .

Зависимость Q ( x , Д ⁽ N ) ) в (18), (19) определяется известным разложением в ряд по собственным функциям рассматриваемой начально-краевой задачи [11], а условия (18), (19) приводятся к единственному ограничению вида (13) при выборе £ ₀ = £ 1 :

-2т f Q ( n , ^д( N ) ) ^- Q ** ^] п d n ^x 0

• (20)    Ф о ( Д ⁽ N ) ) = max « а 1 Q ( x , Д ⁽ N ) ) - Q **| + а ₂ ^£ y e V 1 ^ I I ^£ 2

  < £ 1 ,

  
  

где функция максимума рассматривается в отличие от (18), (19) на расширенном множестве V 1 элементов y = ( x , а 1 , а ₂), содержащем наряду с пространственными переменными x е [0,1] коэффициенты а 1 , а ₂ >  0 , связанные равенством а 1 + а ₂ = 1 .

Решения Д ⁽ N ) ЗПО (17), (20) могут быть найдены по общей технологии применения аль-тернансного метода, описанной в разделе 2, с использованием дополнительной информации о форме кривой пространственного распределения температуры в конце оптимального по быстродействию процесса индукционного нагрева, устанавливаемой на базе физических закономерностей поведения нестационарных температурных полей с внутренними электромагнитными источниками тепла и позволяющей перейти от замкнутой системы соотношений вида (5) к расчётной системе уравнений, разрешаемой относительно всех искомых неизвестных [11].

На рисунках 1, 2 представлены некоторые результаты решения предлагаемым способом задачи (17)-(19) оптимизации процесса индукционного нагрева перед прессованием цилиндрических слитков из титановых сплавов диаметром 0.54 м на промышленной частоте 50 Гц при максимальной поверхностной плотности нагрева 106 кВт/м ² до температуры Q ** = 1050 ° С.

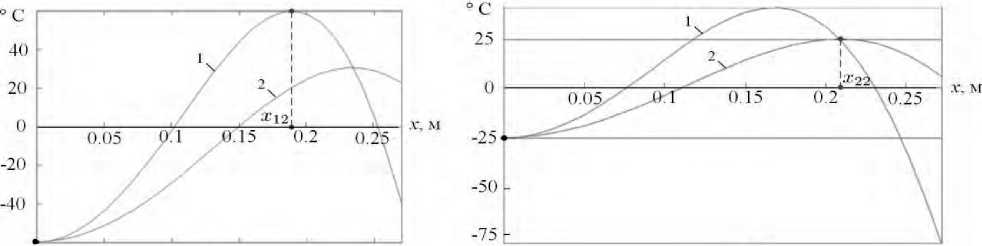
Результирующие распределения температур (1 - для Q(x,Д[k])-Q**, 2 - для Qc(x,Д[к])) в конце оптимального по быстродействию процесса управления с учётом только одного из ограничений (18), (19) при заданных значениях £1 = 60°, £2 = 25° показаны на рисунке 1а ( к = 1, Д^ = 5882c; Д[2] = 605c ) и 1б ( к = 2, Д[12] = 5921c; Д[2] = 883c ), где Д[1] - решение задачи (17), (18), а Д[2]- задачи (17), (19). Как следует из рисунка 1, здесь max|Qc(x,Д[1,)| > £2 и max| Q (x, Д[2]) - Q **| > £1, что свидетельствует о необходимости перехода к решению задачи быстродействия с учётом обоих ограничений, согласно предложенному в [13] вычислительному алгоритму.

а                                                          б

Рисунок 1 - Сравнительный анализ решений задачи оптимального быстродействия с одним ограничением

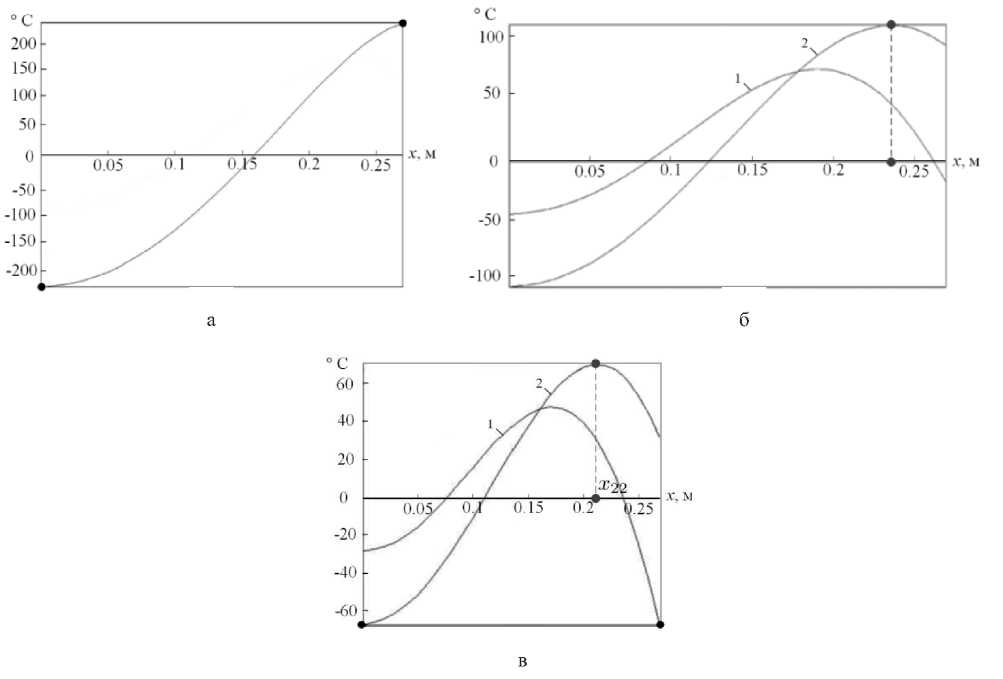
Полученные результаты представлены на рисунке 2 (а - для qQ c ( x , А ⁽¹⁾ при £ — £ 9 = 263 ° ; А 1¹ ) = 6109 c; б - для £ — 105 ° <  £ 2. ; А ⁽ 1^{2 )} = 5983 c , А ⁽ ₂ ^{2 )} = 602 c ; в - для = р* =/'^{(2 )} = 65°      • А^{( 2 )} =5938 с А^{( 2 )}

£     £      £ min           ^' £ 1 ; ^"^1               с , ^д"^х2            c ).

На рисунке 2 (б и в) кривые 1 и 2 иллюстрируют конечные температурные распределения соответственно Q ( x , А ⁽²⁾ ) - Q** и qQ c ( x , А ⁽²⁾ ).

£

Рисунок 2 - Решение задачи оптимального быстродействия с двумя ограничениями q — — — 2 , 4 ^£ 2

Заключение

Разработан конструктивный метод решения широкого круга параметризуемых задач программного оптимального управления системами с распределёнными параметрами в условиях оценки в равномерной метрике целевых множеств управляемой величины, усложняемых векторной формой предъявляемых требований к критериям оптимальности, учитываемым ограничениям на конечное состояние объекта и числу используемых управляющих воздействий. Показано, что на этот круг задач может быть распространён по предлагаемой технологии разработанный ранее авторами для скалярных вариантов специальный альтернансный метод поиска искомых экстремалей, являющийся дальнейшим развитием теории нелинейных чебышёвских приближений.

Работа выполнена при финансовой поддержке РФФИ (проект №18-08-00048).