Alternative to the entropy increase principle

• 2.    Origin of the principles of existence and increase of entropy

• 3.    The basic equation of thermokinetics

• 4.    Non-entropic criteria of evolution and irreversibility

• 5.    From the “thermal death” of the Universe to the entropy circuit in it

• 6.    Conclusion

2.    Origin of the principles of existence and increase of entropy

References

It is known that the theory of heat, barely having arisen, was immediately divided into two independent directions: the theory of heat exchange, the foundation of which was laid by J. Fourier (1822), and thermodynamics, the beginning of which was laid by the equally famous work of S. Carnot (1824) [1]. Both of these works were based on the notion of caloric acid as an indestructible fluid and on the concept of temperature as its potential. However, time as a physical parameter was present only in Fourier [2], which left an imprint on all the subsequent development of 130

these theories. Already in 1822, the work of L. Navier [3] appeared, which marked the beginning of the hydrodynamics of viscous liquids; in 1827, he derived his famous G.Ohm law [4], and in 1855 A. Fick proposed the diffusion equation [5]. These works reflected the kinetics of heat, momentum, charge, substance, etc. transfer processes. The thermodynamics of Carnot [6] and Clausius [7], on the contrary, considered quasi-static (infinitely slow) processes, and the ideas of transfer were alien to it. This for a long time connected thermodynamics with the requirement of reversibility of the studied processes, and the concept of entropy - with the coordinate of heat transfer. The theory of heat transfer, the concept of entropy was still alien.

Both these directions developed independently and after the collapse of the theory of caloric, having no points of contact. Until now, the concept of heat in thermodynamics and the theory of heat transfer remains different. For thermodynamics, this is part of the energy exchange, due solely to the temperature difference between the bodies and not related to the exchange of matter between them. On the contrary, in the theory of heat exchange, heat is considered a part of the internal energy associated with chaotic motion [1].

Such a strange separation of two directions of the same field of macroscopic physics could not overcome the disequilibrium thermodynamics, which is based on the principle of increasing entropy and therefore excludes from consideration the reversible part of real processes [8, 9]. This situation persisted until a unified theory of nonequilibrium processes of heat transfer and transformation was developed, which we called for short thermokinetics [10]. It operates with energy flows and energy carriers, and proceeds from the formulation of the energy conservation law in the form proposed by N. Umov [11], which allowed the synthesis of thermodynamics and heat transfer theory. The approach from these positions allows one to reveal the reasons why “the question of the physical basis of the law of monotonous increase in entropy remains… open” [12] and eliminate the “glaring contradiction of thermodynamics with the theory of biological evolution” [13].

The founder of equilibrium thermodynamics R. Clausius based thermodynamics on the basis of the principle of equivalence of heat Q and W. At the same time, he considered them to be the only two possible ways of energy exchange between an equilibrium system and the environment [7]. In this regard, Clausius was faced with the task of finding the coordinates of heat transfer, that is, a parameter that necessarily changes when heat is applied Q and remains unchanged in adiabatic processesx. Clausius solved it by breaking an arbitrary cycle of a heat engine alongside isotherms and adiabats into an infinite number of elementary Carnot cycles with temperatures of heat supply and removal Т’, Т" элемент and elementary amounts of supplied and removed heat dQ ’ and dQ". The thermal efficiency of an elementary Carnot cycle ntк = 1 — dQ"/dQ ’ — 1 -Т"/ Т’. In this case, the sum of the so-called “reduced heats” dQ/T in an arbitrary circular process vanishes and therefore represents the total differential of a certain state function S, for which f dQ/ Т = f dS = 0,                              (1)

Hence follows the analytical expression of the elementary heat of the equilibrium process:

đQ = ТdS                                      (2)

According to (2), in equilibrium (reversible) processes, the parameter S increases with the supply of heat Q and decreases with its removal ( đQ <  0), which is a necessary and sufficient sign of the presence of equilibrium heat exchange [7]. However, soon R. Clausius discovered that in irreversible processes, expression (2) becomes the inequality đQ <  ТdS . If we assume as a matter of course that the thermal efficiency n t of any irreversible heat engine n t is less than in the ideal Carnot cycle n t ^к at the same heat supply and heat removal temperatures Т ’ and Т ", then the inequality arises:

n t = 1 - dQ "/ dQ ’ < n t ^к — 1 - Т "/ Т ’ . (3)

In this case, dQ ’/ Т ’< dQ "/ Т ", that is, the sum of reduced heats dQ / Т in the cycle of an irreversible machine is less than in a reversible one, where f dQ / Т — f dS = 0:

f 8 Q / Т < 0. (4)

Thus, in adiabatically isolated systems (where đQ = 0), the entropy increases when any irreversible processes occur in it :

dS >  dQ / Т , или dS из > 0, (5)

Not seeing the limitations of this evidence, R. Clausius not only elevated him to the rank of the 2nd law of thermodynamics but also extrapolated to the entire Universe. Such an absolutization of the principle of increasing entropy was expressed most vividly in his catch phrase: “ The energy of the Universe is unchanged. The entropy of the universe is increasing ”[7].

The conclusion that followed about the inevitable "thermal death" of the Universe gave rise to the ongoing discussions and numerous attempts to improve or disprove the evidence given by R. Clausius of this principle. Within the framework of this article, it is impossible to reproduce even parts of the evidence proposed by different researchers on the insolvency of this principle. Therefore, let us refer to the conclusion of the well-known physicist-thermodynamics of Putilov, who gave their most complete analysis: “We don’t find classical and later works on thermodynamics ... a perfectly rigorous justification of thermodynamic inequalities ... Many authors were inclined to consider an incorrigible logical flaw in this part of thermodynamics "[14].

Moreover, it can be shown that such evidence does not exist at all in the framework of equilibrium thermodynamics. Consider for this a fairly general case of a polyvariant system, the state and internal energy of which U is characterized by entropy S , volume V , charge 3 , polarization D , magnetization M , momentum P k of the internal (diffusion) movement of the k -th components of the system and their moments L k , i.e. U = U ( S , V , З , D k , M k , Р k , L k ). Considering the entropy S as an inverse function of these variables S =S ( U, V З , D k , M k , Р k , L k ), we find that in isolated systems ( U, V З , D k , M k , Р k , L k = const) the entropy S iz remains unchanged, like all its arguments [15]:

S из = S ( U , V , З , D k , M k , Р k , L k ) = const. (6)

From a physical point of view, this conclusion is fairly obvious: if the state of a system is described only by conserved parameters, then its entropy as a function of these variables in isolated systems cannot change. This conclusion applies also to L. Boltzmann's statistical-mechanical entropy, which he interprets as a measure of the thermodynamic probability of the state Ω of the form [16]:

S = k ln Ω , (7) where k is a constant, later named after him.

The Boltzmann entropy has the advantage that it can decrease in adiabatically isolated systems as it is ordered. However, it also characterizes the change in the state of the system only as a whole, without detailing them and not indicating the reasons for irreversibility. In addition, the probabilistic interpretation of entropy as a measure of "chaos" indicates only the direction of the process, not allowing to calculate the value caused by the irreversibility of the loss of system performance.

3.    The basic equation of thermokinetics

To avoid any new hypotheses and postulates in the foundations of thermokinetics, we apply a more general deductive approach to finding its basic equation [17]. In this case, we will apply a strictly logical-mathematical method for its justification, which will make transparent those assumptions that were used in this process.

Consider for this purpose the combined equation of the 1st and 2nd principles of the equilibrium thermodynamics of open systems in the form of the Gibbs relation [18]:

dU = TdS - pdV + Σ k µ k dN k , (8) where U , S , V и N k are the internal energy, entropy, volume and number of moles of the k -th component of the system; T , p , µ k is the absolute temperature, its pressure, and chemical potential.

For brevity, further calculations will present this relation in a compact form using the concepts of generalized potentials ѱ i and generalized coordinates Θ i of any i -th process of equilibrium energy exchange of the system with the environment [19]:

dU = Σ i ѱ i d Θ i . (9)

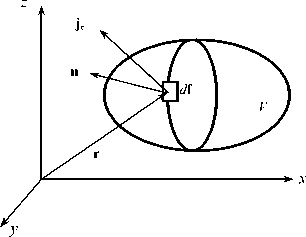
Fig. 1. The flow of energy across system boundaries.

In the equilibrium systems to which this equation belongs, the change in any of the parameters Θi as a quantitative measure of the ith energy carrier is solely due to its transfer across the system’s boundaries. This allows us to express their change in time t by a well-known expression: d Θ i / dt = – ∫ j i · d f ,                                               (10)

where j i = ρ i υ i is the energy flux density Θ i through the vector element d f of the closed system surface in the direction of the outward normal n (Fig. 1); υ i - the speed of its transfer.

Substituting (3) into (2), we have:

dU / dt = – Σ i ѱ i ∫ j i · d f .                                          (11)

Since the generalized potentials ѱ i are the same at all points of the equilibrium system, they can be entered under the sign of the integral: dU/dt = – Σ i ∫ψ i j i ^e d f ,                                          (12)

The value ψiji is the i – th component of the energy flux density ju = Σiψiji through the df element of the system surface (Fig. 1). Passing in (12) on the basis of the Gauss – Ostrogradsky theorem from f the surface integral ∫ψijidf to the integral ∫∇⋅(ψiji)dV over the volume of system V, we arrive at a generalized expression of the energy conservation law for an arbitrary region of the continuum proposed by N. Umov in 1873 [11 ]

dU/dt = – ∫ ∇⋅ j u dV (13)

Representing the divergence ∇⋅ j u = Σ i ∇⋅ (ψ i j i ) as the sum of two terms Σ i ψ i ∇⋅ j i + Σ i j i ∇ ψ i , we find:

dU/dt = – Σ i ∫ψ i ∇⋅ j i dV + Σ i ∫ x i · j i dV , (14) where x i ≡ – ∇ ψ i is a quantity called in the thermodynamics of irreversible processes (TIP) “thermodynamic force in its energy representation” [19].

The members of the first sum in this expression contain the divergence of the energy flow j i across the system’s boundaries and therefore characterize that part of the energy exchange that is associated with external sources of parameters Θ i = ∫ρ i dV , including the entropy S and its density ρ s . This type of energy exchange is referred to in thermokinetics for short as energy transfer since it is not associated with energy conversion. Such are heat exchange, mass transfer, diffusion of k -x substances, exchange of space occupied by the system (its expansion or compression under conditions of equal pressure with the environment), etc. When such processes are quasi-static (infinitely slow), they do not disturb the equilibrium in the system, which and makes them the object of study of classical thermodynamics.

The processes described by the members of the 2nd sum (7) have a different character. These processes, even being quasistatic, redistribute the energy carrier Θ i = ∫ρ i dV over the volume of the system V under the action of force x i , thus causing its center to shift with the speed υ i = d r i /dt . In this case, an internal work x i ∙d r i is performed, which characterizes the process of polarization of the system in its most general understanding, i.e. transformation of the i -th form of energy into some j -th of its form. This process in thermokinetics is called energy conversion .

If we now take out the integral value in (14) some average value некотороеi of potential Ψ i , velocity υ i and gradient ∇ ψ i and apply the same Gauss – Ostrogradsky theorem, we can give it a form describing the behavior of a nonequilibrium system as a whole ^: (here the rule of signs for heat and work accepted in thermodynamics is preserved: the heat brought to the system and the work done by it are considered positive)

dU/dt = Σ i Ψ i d Θ i / dt – Σ i X i · J i , (15) where J i = Θ i υ _i = ∫ j i dV is the total flow of energy carrier Θ i in a heterogeneous system (having the meaning of its impulse); X i = J i ^-1 ∫ x i · j i dV is the average value of the thermodynamic force.

Equation (15) is fundamentally different from (2) by explicitly taking into account the disequilibrium of the systems under study and the speed of real processes with the help of intensive Xi and extensive Zi = ΘiRi parameters of spatial inhomogeneity. With this approach, the thermodynamic forces Xi and the fluxes Ji are found directly as derivatives of the system energy U according to these parameters Xi = - (∂U/∂Zi) and like a derivatives of them in time Ji = dZi/dt. This frees up the need to attract a number of other disciplines to find and build on their basis the cumbersome balance equations of entropy, energy, mass, charge, momentum, etc. [19]. This eliminates the characteristic for TIP arbitrariness in dividing the rate of increase in entropy dS/dt into factors Ji and Xi, making it difficult to understand their meaning and affecting some of the results of its application.

It is easy to see that for Xi, Zi = 0 and Ψi = ψi, equation (15) takes the form (8). This means that the energy of non-equilibrium systems as a function of their state in the case under consideration has the form U = U(Θi, Ri). The latter testifies to the failure of the local equilibrium hypothesis, according to which the state of the elements of the nonequilibrium continuum is characterized by the same set of variables as in equilibrium (despite taking into account the presence of forces Xi in them). In this case, the total differential dUi of any i-th (partial) energy Ui can be represented as the sum of 2 terms dUi = Ψi dΘi + Θi dΨi, (16) the first of which characterizes the increment of energy Ui due to its transfer across the system’s borders, and the second due to the transformation of its other, jth forms. Thus, any partial energy Ui is expressed by the product of the intense Ψi and extensive measure Θi. If the system is homogeneous (Ψi ≡ ψi), then Ui = ψiΘi. Such are, in particular, the pressure p and the volume V for the internal energy of the elastic deformation of the gas or the chemical potential µk and the number of moles Nk of the kth component of the equilibrium system. The internal heat energy Uq = TS , where T , S is the average temperature of the system and its entropy, which in equilibrium systems is identical to the Helmholtz “bound energy” Uq = TS, does not constitute an exception. This is directly related to the principles of the existence and increase of entropy.

4.    Non-entropic criteria of evolution and irreversibility

From the standpoint of thermokinetics, let us consider the problem of justifying the existence of entropy, which a number of researchers [20, 21] quite reasonably separated from the principle of its growth in irreversible processes. It is easy to notice that the internal heat energy Uq is equal to the quantity, which founder of equilibrium thermodynamics R. Clausius “full body heat,” meaning under it the sum of the heat Q and body heat Q9 supplied to the body as a result of the dissipative nature of the “work of disgregation”. Such an understanding of body heat has developed historically in connection with considering it along with such phenomena as light, sound, electricity, magnetism. It has been preserved despite hot discussions in the concept of the body heat capacity, in the law of thermal conductivity of Fourier [2], as well as in the definition of the heat exchange process [1].

In non-equilibrium systems, such an understanding of heat is dictated by the existence of thermal effects not related to heat exchange and caused by energy dissipation (friction, high-frequency or induction heating, chemical transformations). Only in equilibrium systems, where such effects are absent, does the heat turn out to be associated exclusively with the heat exchange process and becomes a quantitative measure of this process. Given this duality in the understanding of heat, thermokinetics distinguishes between “body heat” and “process heat”, which are respectively a function of state and a function of the process, and to avoid confusion, denotes the first through U q and the second through Q .

In this case, the existence of the entropy of a thermally inhomogeneous system S = U q / T as a quotient of dividing one system parameter ( U q ) by another ( T ) is no longer in doubt. This frees us from the need to look for ways to prove the fact of the existence of entropy in thermally inhomogeneous media, which even for equilibrium systems look very cumbersome and not obvious [22].

Further, according to (7), the term ∫ Т ∇⋅ j is dV = T dS/dt characterizes the increase in entropy solely due to its flow through the system’s boundaries, i.e. due to heat exchange, the ratio

đQ = T dS (17) gives an accurate expression of heat in the processes of non-equilibrium heat transfer, not turning into inequality for irreversible processes. This is how the problem of thermodynamic inequalities is solved, which sharply limited the range of applicability of classical thermodynamics.

At the same time, the physical meaning of this parameter is also exposed. Comparing (17) with a similar expression of the elementary work of accelerating a system of k -th bodies đW = = Σ k υ _k ∙ d J k , where υ _k , J k is the average speed and impulse of their ordered movement expressed in the same analytical form:

đQ = T dS ; đW = Σ k υ _k ∙ d J k , (18)

It follows from (9), that the entropy S plays in relation to the thermal energy U q the same role as the impulse J k in relation to the kinetic energy of the flow Е k . In other words, entropy is a “ thermoimpulse ”, i. e., a pulse of thermal motion of particles that has lost its vector nature due to the randomness of this motion.

It is quite natural that the thermal impulse S increases both as a result of heat supply đQ from the outside and as a result of the transformation of ordered forms of energy into a disordered đQ ^∂ in a nonequilibrium system, i.e.

dU q = đQ + đQ ^∂ = T dS + Sd T (19)

It is easy to see that multiplying and dividing the Sd T term by υ _s it can be expressed in the form X s ∙ J s , which characterizes the source of entropy in the thermodynamics of irreversible processes [9], where X s = ∇ Т is the driving force of the heat conduction process; J s = d Z s /dt = S υ _s is the entropy flow.

From (19) it also follows that the heat of dissipation

đQ ^∂ = Sd T (20) is expressed in reality by an increase in the average temperature of the system, and not by an increase in its entropy S .

This has been convincingly shown in a series of experiments by L. Brovkin (1960, 1964) [23]. In these experiments, a sensitive element of a resistance thermometer was laid into the gap of a tightly packed roll of paper, cardboard, rubber tape and other sheet materials. Then the roll was subjected to uneven heating from an external heat source, after which a spontaneous process of thermal relaxation occurred in it. At the same time, a change in the resistance of such a “dispersed” thermometer was recorded. Surprising in these experiments was the fact that in all the tested materials there was a significant (reaching 17%) rise in the average integral body temperature. It lasted for tens of minutes until the decrease in temperature due to cooling of an insufficiently insulated roll began to prevail. At that time, this phenomenon called the “growth effect of the measured heat content,” was not satisfactorily explained.

Meanwhile, it directly follows from relation (20) as the result of the transition of the ordered part of the thermal energy to the unordered one. A good example of such dissipation of thermal energy is thermal relaxation, which leads to equalization of temperature in different parts of the system (Хq → 0) and to the disappearance of the “driving force of heat” in the theory of thermal machines by S. Carnot [3]. Thus, in thermal energy one should distinguish an ordered part capable of dissipation, and not relate it entirely to the chaotic form of motion. This dissipation is expressed by the Sd T member. The presence of this term reveals the incorrectness of the division of the total entropy differential dS into the components dеS and diS proposed by I. Prigogine, which change accordingly when heat is supplied from outside đQ = ТdеS and when internal sources of entropy diS appear due to dissipation đQ∂ = ТdiS [24]:

dU q = dQ + dQ ⁹ = Td e S + Td i S . (21)

For some reason, such a decomposition of the independent variable into parts has not caused experts' objections, although it goes beyond the framework of mathematics. In the same way, we could break the differentials of other independent parameters Θ i , thereby depriving them of the conservation properties (the latter, as is known, is determined precisely by the form of their balance equation, that is, the presence or absence of internal sources in it [16]).

It is possible to show that internal sources are available not for energy carriers Θ i and for the partial energy of U i which can change not only owing to its supply or branch through system borders but also owing to internal transformations of some forms of energy into others. To show it, we will write down (15) for isolated systems ( dU/dt = 0 ) in a look:

dU/dt = Σ i d (Ψ i Θ i )/ dt – Σ i Θ i d Ψ i / dt – Σ i X i · J i = 0, (22) Since dU/dt = Σ i dU i /dt= Σ i d (Ψ i Θ i )/ dt , in non-equilibrium systems

Σ i Θ i d Ψ i / dt = – Σ i X i · J i . (23)

In equilibrium systems ( X i = 0), this expression transforms into the generalized Gibbs – Duhem relation Σ i Θ i d Ψ i = 0, as one would expect [18]. Thus, expression (23) allows us to distinguish the equilibrium part U = Σ i Ψ i Θ i of the internal energy of the system U . The rest (non-equilibrium) part U - U generalizes the concept of the Helmholtz free energy. It characterizes the performance of the system as a whole and each form of its partial energy U .

d U j = - S i X i • d Z i ; d U i = - X i • d Z i . (24)

In the particular case when internal sources are only in entropy, that is, ΣiΘidΨi/dt = -ТdiS = Sd T , equality (23) goes into the well-known expression of the dissipative function of TIP ТdiS = Σi Xi·Ji. However, internal sources are available not only for heat but also for any other forms of partial energy of a polyvariant system. This is confirmed by a number of experimental facts indicating that dissipation does not boil down to thermal effects. It is known, for example, that when cutting metals, the amount of heat generated by friction Q∂ is often less than the work expended because part of the energy expended goes into the internal energy of the chip. This fact is confirmed experimentally by the difference between the isothermal heats of dissolution of the initial and deformed material. The same is observed in the processes of crushing of bodies, in which, along with the thermal energy, the surface energy of the powder increases.

In technology, both of these effects are taken into account by introducing a “heat output coefficient” smaller than one. Also known is the effect of increasing temperature in the flow part of steam and gas turbines due to friction, which is taken into account by the “heat recovery coefficient”. The numbers of moles N k of k -x substances of chemical reaction products, strain tensors of plastic materials, etc. behave in a similar way. An “indirect impact” of bodies is no exception, as a result of which the momentum of the translational motion of bodies decreases and the amount of rotational movement increases. From this point of view, the very idea of Clausius to describe all the processes of dissipation by the parameters of only one (thermal) degree of freedom looks at least strange. This tacit assumption made entropy a scapegoat for any irreversible state changes, i.e., a measure of “any and all” irreversibility. The costs of this indiscretion are still felt [15].

Thus, thermokinetics reveals the fundamental inconsistency of the principle of increasing entropy in isolated systems, which is considered to be almost the main expression of the 2nd law of thermodynamics. In this regard, the need to find non-entropic criteria of evolution and irreversibility becomes obvious. Thermokinetics allows to solve this problem due to the introduction of its nonequilibrium parameters (force X i , moment Z i and displacement vector R i ) Any of these variables characterizing the removal of the i -th degree of freedom of the system from the state of equilibrium (its evolution), while the decrease - involution (degradation) [25]:

d X i , d Z i , d R i > 0 (evolution); d X i , d Z i , d R i < 0 (involution). (25)

The same parameters allow you to find the loss of performance caused by the relaxation of the system for any degree of its freedom and the system as a whole:

d U i = - X i • d Z i < 0; d U = - S i X i • d Z i < 0, (26) as well as the power of energy dissipation processes:

d U i / dt = - X i • J i ; d U / dt = - S i X i • J i . (27)

The principle of increasing entropy, which is the cause of most paralogism of thermodynamics [15], becomes superfluous. All this testifies to the need to reformulate the 2nd law of thermodynamics with the exception of the mention of entropy. For example, the following statement is quite acceptable: “Any irreversible processes in thermodynamic systems lead to the transformation of ordered forms of its energy into unordered and loss of its efficiency”. This formulation is not only more “physical” but also applicable to open non-isolated systems, that is, it is more general.

5.    From the “thermal death” of the Universe to the entropy circuit in it

The principle of increasing entropy imposes a "time arrow" on the Universe and prophesies inevitable death to it. Meanwhile, the fact that thermal equilibrium did not occur in it for at least 13–14 billion years of its existence1) allows us to conclude that it develops, bypassing the state of equilibrium. This is explained by the fact that, according to observational astronomy, only 4.9% of the substance of the Universe is visible, while the rest of it is not involved in electromagnetic interactions and therefore is not observable [26]. The existence of two phases of a single material environment, which, for brevity, we call baryon (structured) and nonbarion (non-structured), puts on the agenda the study of the features of their mutual transformation. The concept, which the author adheres to [27], is based on the recognition of the existence of a “hidden mass” of the Universe, which is compressed by the forces of condensation and condenses into baryon (ordinary, observable) matter consisting of protons, neutrons, electrons, etc. elementary particles . The latter, with further compaction, forms all types of celestial bodies, uniting into atoms, molecules, gas-dust clouds, small and large celestial bodies, and their clusters.

Moreover, in addition to the gravitational form of energy, it acquires its other forms (thermal, electromagnetic, chemical, etc.). The oscillations of the material carriers of these forms of energy generate radiation with a spectrum that differs from the background, which makes the baryonic matter of the Universe observable [28]. As celestial bodies condense, accompanied by their heating, the internal stresses in them increase and at a certain stage of evolution, they begin to exceed the compressive forces. Then comes the so-called "supernova explosion", turning into a "big gap" of atomic and nuclear structures. As a result of these destructive processes, a part of the baryon substance returns to its original form.

This process also affects entropy, since, with the disappearance of baryonic matter as such, its internal thermal energy disappears, along with entropy as its extensive measure. If we consider it as a function of the absolute temperature T and the volume V of the Universe as a whole, that is, S = S ( Т , V ), then its total differential has the form:

dS = ( д S/ д T) v dT + ( д S/ д V) т dV (25)

The first term of this expression is easily converted to the form С v dlnT , where C v = ( d U/ д Т) v is the isochoric heat capacity of the baryon part of the matter of the Universe. With a “supernova explosion,” accompanied by a sharp increase in its luminosity and a subsequent decrease in temperature, this term is negative. In closed systems, the resulting decrease in entropy would be partially compensated by the second term, which characterizes the increase in entropy due to its expansion. However, an explosion does not result in the expansion of a “supernova”, but the scattering of its substance with an increase in the kinetic energy of the “fragments”. Therefore, in the process of transformation of a baryon substance into a non-baryon, its entropy decreases to zero, no matter what level it reaches before. Thus, the question of the “thermal death” of the Universe is finally solved.

From this point of view, one has to admit that in the Universe at the same time, the oppositely directed processes of evolution in non-barion and in involution occur in the baryon phase of its matter (or vice versa). This reflects their dialectical nature and excludes the possibility of talking about the "arrow of time" for the universe as a whole.

6.    Conclusion

emergence of thermodynamic inequalities for irreversible processes and reveals the fallacy of the principle of increasing entropy.