Альтернативный метод построения корреляционных моделей колебательных процессов

Автор: Ш. Б. Очилов, О. К. Акрамова, Н. Н. Расулова

Журнал: Informatics. Economics. Management - Информатика. Экономика. Управление.

Рубрика: Системный анализ, управление и обработка информации

Статья в выпуске: 4 (1), 2025 года.

Бесплатный доступ

В данной статье изучаются экономические процессы, имеющие корреляционную зависимости, которые меняются с течением времени по гармоническому закону, а также предлагается способ нахождения периода, фазы и частоты колебания процессов. В результате исследований в статье предложен метод определения коэффициентов А и В в гармонической функции. Выполнено сопоставление реальных и модельных данных. Отмечается, что колебательные процессы урожайности сельскохозяйственных культур рассмотрены в научных работах российских ученых, которыми была установлена закономерность колебания урожайности зерновых культур. Предлагается усовершенствованная методика по определению циклов урожайности хлопчатника, которая в отличие от ранее предложенных подходов, посвяшенных определению циклов колебаний урожайности сельскохозяйственных культур, когда циклы определяются при помощи сопоставления большого количества информации за длительный период времени, позволяет определить цикличность процесса, имея даже минимальное количество наблюдений. Приведены результаты расчётов и данные, на основе которых определяется существование циклов колебания урожайности хлопчатника на примере Бухарской области Республики Узбекистана. Методика апробирована на основе конкретного примера, который подтвердил ее практическую пригодность для решения поставленной задачи.

Еще

Дифференциальное уравнение, конечные разности, период колебания, частота колебания, гармонические функции, цикличность колебания урожайности сельскохозяйственных культур, фаза колебания

Короткий адрес: https://sciup.org/14132659

IDR: 14132659 | DOI: 10.47813/2782-5280-2025-4-1-2001-2009

Текст статьи Альтернативный метод построения корреляционных моделей колебательных процессов

DOI:

Многие процессы в природе происходят на основе колебательных законов. По результатам экспериментов легко определяются основные характеристики, такие как период колебания, частота, фаза колебания и амплитуда, если зависимости являются функциональными. Например, колебания электромагнитных волн, колебания математического маятника. Но когда изучаются процессы, имеющие корреляционные зависимости, задача усложняется, так как требуется нахождение периода колебания, амплитуды и других показателей. При этом необходимо изучить и сопоставить большие объемы данных за длительный период.

В этой работе сделана попытка ответить на следующие вопросы:

• Возможно ли установить, что процесс у i =f(x i ) является гармоническим, если известны результаты экспериментов над процессом Т в точках х i и у i ? Имеется ли некоторый математический критерий проверки

правильности этого утверждения?

• Как определить способ нахождения периода колебания, частоты и фазы колебания?
• Как можно определить коэффициенты А и В, если в результате исследования получена гармоническая функция:

у = Asin(ыx) + Вcos(ыx)?

MATEРИАЛЫ И МЕТОДЫ

При решении практических задач у исследователей часто возникает вопрос, не является ли данный процесс колебательным процессом? Этот вопрос возникает в ряде случаев, таких как: изучение урожайности сельскохозяйственных культур, изучение колебания спроса на товары и услуги в зависимости от сезона, изучение периодичности возникновения землетрясений в сейсмоактивных зонах.

Колебательные процессы урожайности сельскохозяйственных культур рассмотрены в научных работах российских ученых, в которых установлена закономерность колебания урожайности зерновых культур [1-3]. На основе изучения длительных временных рядов авторами было установлено существование некоторого цикла колебаний урожайности, а также установлена закономерность этого процесса [4, 5]. Также в журнале «Хлопководство» было опубликовано несколько статей, в которых была

сделана попытка доказать существование цикличности колебания урожайности во всех хлопкосеющих республиках бывшего Советского Союза. Также было доказано, что эти закономерности действуют и для других сельскохозяйственных культур. Для доказательства того, что тот или иной изучаемый процесс является циклическим процессом, необходимо проанализировать огромное количество статистических данных, проверить их на синхронность, сопоставить графики этих явлений и многое другое [6, 7].

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Возникает вопрос, возможно ли определить, что изучаемый процесс является колебательным (гармоническим) процессом, если известны результаты наблюдения в ограниченных точках? Для этого имеется конечное число точек х i и y i , где i = 1,N. Также необходима математическая разработка критерия, при выполнении которого функция y i = f(x_i) будет точно гармонической, а никакой-то другой.

Предположим, что у нас имеется функция у = f(x) и эта функция гармоническая:

у = Asin—+ В cos—.

J т т

Для определения критерия производные — и ^^ :

dx dx2

dy _д 2л 2nx

dx Т

—

-а(—)2 sin —-

ТТ

$ 2л . 2лх

Т Т

b(—)²cos — .

ТТ

вычисляем

d2y dx2

С учетом того, что у =A sin^^+Bcos 2^ , имеем

^= - (—)2 (Asin—+ В cos—) или — =

dx2 Т Т Т dt2

-^гу. Л

Другими словами, ^^ = у" = -ы2у, где ы = 2^. Здесь T является периодом колебаний, а 1-частотой колебания рассматриваемого процесса. Отсюда следует, что у"

— = -ы2 = const. (1)

Условие (1) и является критерием гармоничности процесса у = f(x).

Таким образом, если для процесса у = f(x) отношение — постоянно является константой, У

то этот процесс является гармоническим

процессом.

Так как мы не имеем конкретной функции процесса y_t = f (х ^ ), а имеем только результаты наблюдения в некоторых точках x i и y i , где i = -з— dy d²y 1,N , то постараемся заменить — и — конечными разностями, которые выражаются через x_i и y i , i = 1, N.

имеем

; ^ j- у".

Если у = f(x) непрерывная функция и имеет непрерывные производные 1-го и 2-го порядка, то из определения производной у ' = f'(х₀)

Поэтому производные приближенно можно заменить конечными разностями:

' _ dy Ау „ _ d2y А2у у dx Ах , у dx2 Ах2 .

lim

Ах—О

у(х0 + Ах) - у(хр) Ах

Ау ,

= limbA-^ (Хо) =У Ах-0 Дх

имеем

^у ( ^{Хо+Ах)-у} ( ^Хо) ^ _(Жо ) = у, или АУ ^ f '(х о ) = у,;

Аж ^{J у} Ах ^J ^{у ;}

На основе этого, наш критерий цикличности функции формулируется в следующем виде: если известны результаты эксперимента х i и y i , то необходимым условием цикличности процесса является выполнение условия

А2у

— /у = const.

Ах2

По определению производной второго порядка у '' = f"(x o )

lim

Ах—О

у'(хр + Ах) -у'(хр) Ах

= у''

lim w = f''(x0)Ах-о Ах2 0

Вышеуказанный критерий можно рассмотреть на следующем конкретном примере. При этом А2у условие ^т; /у =const играет важную роль при правильном выборе функции у = f(x).

Таблица 1. Совпадение значений гармонический функции Y 1 и прямой линии в Y 2 в определенных интервалах значения «х».

х	у 1 = 3sin(23,14х/5)	у 2 = 2,8591x + 0,2151	у 1 - у 2
0,035	0,131837528	0,3151685	0,183331
0,07	0,263420324	0,415237	0,151817
0,105	0,394494146	0,5153055	0,120811
0,14	0,524805739	0,615374	0,090568
0,175	0,654103318	0,7154425	0,061339
0,21	0,782137057	0,815511	0,033374
0,245	0,908659575	0,9155795	0,00692
0,28	1,033426407	1,015648	-0,01778
0,315	1,156196483	1,1157165	-0,04048
0,35	1,276732591	1,215785	-0,06095
0,385	1,394801834	1,3158535	-0,07895
0,42	1,510176082	1,415922	-0,09425
0,455	1,622632412	1,5159905	-0,10664
0,49	1,73195354	1,616059	-0,11589
0,525	1,837928239	1,7161275	-0,1218
0,56	1,940351747	1,816196	-0,12416
0,595	2,039026165	1,9162645	-0,12276
0,63	2,133760837	2,016333	-0,11743
0,665	2,224372719	2,1164015	-0,10797
0,7	2,310686734	2,21647	-0,09422
0,735	2,392536109	2,3165385	-0,076
0,77	2,469762696	2,416607	-0,05316
0,805	2,542217281	2,5166755	-0,02554
0,84	2,609759868	2,616744	0,006984
0,875	2,672259955	2,7168125	0,044553
0,91	2,729596781	2,816881	0,087284
0,945	2,78165956	2,9169495	0,13529
0,98	2,828347698	3,017018	0,18867
1,015	2,869570988	3,1170865	0,247516

В таблице 1 приведены данные эксперимента, связывающие х i и y i . На первый взгляд кажется, что это обычная линейная связь у =а₀+йх между х и у. Обработка данных осуществлена с помощью традиционных методов и получен следующий результат: у₂ = 2,8591х + 1,2151. При этом коэффициент корреляции r = 0,98, а также разность между фактическами и

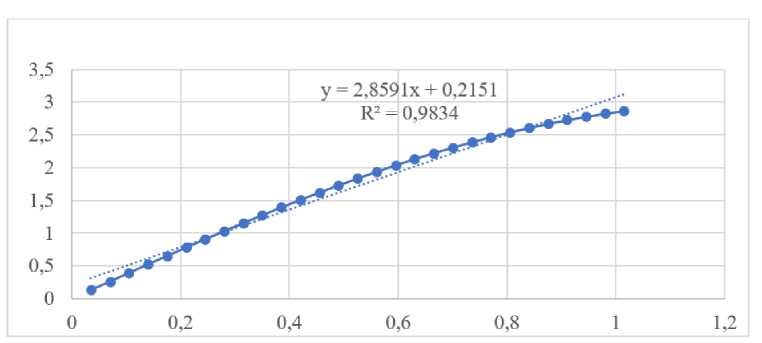
Рисунок 1. Сопоставление реальных и модельных значений.

расчетными значениями |у ф -у_р|~0. Но на самом деле это не так. Приведенные данные являются значениями функции у 1 = 3sin(1,256x). Если на графике рассмотреть значения функции у 2 =2,8591х+0,2151 и значения у 1 = 3sin(1,256x) (рис. 1), то можно увидеть, что они практически не отличаются.

Это и является основной причиной наших исследований. Другими словами, необходимо найти математическое утверждение, которое дает четкий ответ на вопрос о форме связи между

Поэтому наша функция выглядит следующим

образом: y = 3,5sin(1,1х) =

3,5sin(Sx).

Для

данными х i и гармоническая

yi: линейная у = а0+bх или у /sin —+B cos—. Т Т

проверки пригодности модели и для доказательства состоятельности предлагаемого метода сопоставлены расчетные и реальные данные.

Необходимое условие, обеспечивающее существование гармонической зависимости между х i и y i , было изложено в формуле (1). Для проверки правильности нашей теории рассмотрим пример, который приведен в таблице 2.

В седьмом столбце этой таблицы подсчитаны значения конечной разности II порядка ~уг /у и вычислено их среднее значение -1,13= -w², отсюда w = V1,13 = 1,06. Так как w² = (у) = А²У

-^2- / y _t, то в этом случае можно найти период колебания Т:

2тт 6,28

Т = — =jy =5,7сек; и w = 1,1r/c.

Амплитуда колебания процесса А находится следующим образом yt = Asin(1,1x).

Из таблицы 2 при х=0,63 имеем 2,1337 = Asin(1,1 * 0,63) и отсюда находим, что A=3,5.

В Таблице 2 значения х i с равным шагом отставания 0,035 и поэтому Ax i =Ax=0,035, Ах² = Ах² = 0,01225. В таблице 2 приведены результаты расчёта средних значений |у р — У ф | = 0,0845.

Таким образом мы можем сделать следующие выводы:

Если известны результаты экспериментов, т.е. значения x i и y i , i = 1,N, то можно определить, является ли зависимость у = /(х) гармонической или нет.

Для определения гармоничности функции у = А²у

/(х) вычисляем конечную разность ^у; и ее отношение к у: если —^/y = cont = w2 то

Ах² изучаемая зависимость является гармонической, т.е. имеет вид

у = /sin—+ BCOS—.

ТТ

Таблица 2. Сопоставление реальных и модельных данных функции y=3,5sin ( |^ x ) .

х	Y	∆y	∆y/ω∆x	∆²y	∆²y/ω∆x²	(∆²y/ω ∆x²)/y	Yp	Y ф -Yр
0,0350	0,1318	0,1316	2,9932	-0,0116	-0,2634	-1,9977	0,1347	0,0029
0,0700	0,2634	0,1311	2,9817	-0,0173	-0,3944	-1,4973	0,2692	0,0058
0,1050	0,3945	0,1303	2,9643	-0,0231	-0,5247	-1,3301	0,4034	0,0089
0,1400	0,5248	0,1293	2,9413	-0,0287	-0,6540	-1,2462	0,5369	0,0121
0,1750	0,6541	0,1280	2,9125	-0,0344	-0,7820	-1,1955	0,6696	0,0155
0,2100	0,7821	0,1265	2,8781	-0,0399	-0,9085	-1,1616	0,8013	0,0192
0,2450	0,9087	0,1248	2,8382	-0,0454	-1,0333	-1,1371	0,9319	0,0232
0,2800	1,0334	0,1228	2,7928	-0,0508	-1,1560	-1,1186	1,0610	0,0276
0,3150	1,1562	0,1205	2,7419	-0,0561	-1,2765	-1,1041	1,1886	0,0324
0,3500	1,2767	0,1181	2,6858	-0,0613	-1,3946	-1,0923	1,3145	0,0377
0,3850	1,3948	0,1154	2,6245	-0,0664	-1,5099	-1,0825	1,4383	0,0435
0,4200	1,5102	0,1125	2,5582	-0,0713	-1,6224	-1,0743	1,5601	0,0499
0,4550	1,6226	0,1093	2,4868	-0,0761	-1,7317	-1,0672	1,6795	0,0569
0,4900	1,7320	0,1060	2,4107	-0,0808	-1,8376	-1,0610	1,7965	0,0645
0,5250	1,8379	0,1024	2,3299	-0,0853	-1,9400	-1,0556	1,9108	0,0728
0,5600	1,9404	0,0987	2,2446	-0,0896	-2,0387	-1,0507	2,0222	0,0819
0,5950	2,0390	0,0947	2,1550	-0,0938	-2,1334	-1,0463	2,1307	0,0916
0,6300	2,1338	0,0906	2,0612	-0,0978	-2,2240	-1,0423	2,2360	0,1022
0,6650	2,2244	0,0863	1,9635	-0,1016	-2,3103	-1,0386	2,3380	0,1136
0,7000	2,3107	0,0818	1,8619	-0,1052	-2,3922	-1,0353	2,4365	0,1258
0,7350	2,3925	0,0772	1,7567	-0,1086	-2,4694	-1,0321	2,5314	0,1388
0,7700	2,4698	0,0725	1,6482	-0,1117	-2,5418	-1,0292	2,6225	0,1528
0,8050	2,5422	0,0675	1,5365	-0,1147	-2,6093	-1,0264	2,7098	0,1676
0,8400	2,6098	0,0625	1,4217	-0,1175	-2,6718	-1,0238	2,7931	0,1833
0,8750	2,6723	0,0573	1,3043	-0,1200	-2,7292	-1,0213	2,8722	0,1999
0,9100	2,7296	0,0521	1,1843	-0,1223	-2,7812	-1,0189	2,9470	0,2174
0,9450	2,7817	0,0467	1,0621	-0,1243	-2,8279	-1,0166	3,0175	0,2359
0,9800	2,8283	0,0412	0,9377
1,0150	2,8696

Одним из достоинств этого метода является то, что, зная только значения х_i и y i , i = 1,N , мы можем определить и период колебания Т, и амплитуду колебания А и В;

Амплитуда А и В определяется на основе решения дифференциального уравнения второго порядка, имеющего вид у" = -ш²у. При этом характеристическое уравнение к²= - ω имеет мнимое решение. Поэтому общее решение дифференциального уравнения имеет вид у =AsinVwt + Bcos^Mt.

Коэффициенты этой функции определяются на основе начальных условий у(х₀) = у₀ ,у'(х 0 ) = у 0 . Исходя из этих начальных условий получим систему из двух уравнений с двумя неизвестными, решив которую находим коэффициенты А и B.

Для проверки этой теории на практике рассмотрим конкретные данные об урожайности хлопчатника в период 1991-2023 гг. на примере Бухарской области Республики Узбекистан.

Ещё в конце XX века М.А. Абдуллаева доказала существование цикличности урожайности хлопчатника, результаты которых были опубликованы в 1982-1984 годах в журнале «Хлопководство». Автором был предложен график урожайности на длительной период на основе определенной цикличности.

Основываясь на этом доказательстве, нами предлагается усовершенствованная методика по определению этих циклов.

При этом Д^ = 1.

Таблица 3. Таблица расчетов для определения циклов колебания урожайности хлопчатника на примере Бухарской области Республики Узбекистан.

t	у i	k i =y i -25,8	ДК △ t ;	△ ²к ; △ t ?	△ ²к_; , ---5-/fci = w ? △ t ?
1.	34,00	8,20	-2,00000	4,90000	0,59756
2.	32,00	6,20	2,90000	-5,60000	-0,90323
3.	34,90	9,10	-2,70000	3,90000	0,42857
4.	32,20	6,40	1,20000	-6,00000	-0,93750
5.	33,40	7,60	-4,80000	5,50000	0,72368
6.	28,60	2,80	0,70000	-0,50000	-0,17857
7.	29,30	3,50	0,20000	1,60000	0,45714
8.	29,50	3,70	1,80000	-5,80000	-1,56757
9.	31,30	5,50	-4,00000	3,80000	0,69091
10.	27,30	1,50	-0,20000	1,30000	0,86667
11.	27,10	1,30	1,10000	0,00000	0,00000
12.	28,20	2,40	1,10000	0,20000	0,08333
13.	29,30	3,50	1,30000	-1,00226	-0,28636
14.	30,60	4,80	0,29774	-1,77444	-0,36968
15.	30,90	5,10	-1,47670	2,34451	0,45991
16.	29,42	3,62	0,86780	-5,35104	-1,47777
17.	30,29	4,49	-4,48324	7,27765	1,62128
18.	25,81	0,01	2,79441	-0,40895	0,00000
19.	28,60	2,80	2,38546	-0,77092	-0,27533
20.	30,99	5,19	1,61454	-2,71454	-0,52349
21.	32,60	6,80	-1,10000	1,00000	0,14706
22.	31,50	5,70	-0,10000	0,00000	0,00000
23.	31,40	5,60	-0,10000	1,40000	0,25000
24.	31,30	5,50	1,30000	-3,70000	-0,67273
25.	32,60	6,80	-2,40000	1,50000	0,22059
26.	30,20	4,40	-0,90000	-0,10000	-0,02273
27.	29,30	3,50	-1,00000	2,80000	0,80000
28.	28,30	2,50	1,80000	-4,20000	-1,68000
29.	30,10	4,30	-2,40000	11,30000	2,62791
30.	27,70	1,90	8,90000	-17,90000	-9,42105
31.	36,60	10,80	-9,00000
32.	27,60	1,80
				средний	-0,27805
				ω	0,52730
				Т	11,90963

В таблице 3 приведены результаты расчётов и данные, на основе которых определяется существование циклов колебания урожайности хлопчатника на примере Бухарской области Республики Узбекистана. Во втором столбце приведены данные об урожайности хлопчатника в период 1991-2023 гг. В третьем столбце осуществлено нормирование данных к i =y i ̶ y min = y i ̶ 25,8. В четвертом и в пятом столбцах

- „ . — _ дк; д2к отражены данные — и -—.■ . И в последнем столбце приведено значение ы2 = △К_ /у. в таблице 3 в 85 процентах данные по модулю всегда меньше единицы. Поэтому в качестве |ш21 берем их среднее значение: |ш2| = 0,27805 и О) 0,5273. Так как у = ы, в этом случае находим, 2л- 6,28

что Т = — = _{Q S273} = 11,9.

В работах, посвяшенных определению циклов колебаний урожайности сельскохозяйственных культур, циклы определяются при помощи сопоставления большого количества информации за длительный период времени. Но при помощи предлагаемого метода можно быстро определить цикличность процесса, имея даже минимальное количество наблюдений. Можно также определить период Т и амплитуду колебаний А.

На основе простых математических расчётов можно определить амплитуды колебания. Как известно А и В определяются с учётом начальных условий. Поэтому мы имеем:

( у = Asinat + Bcosat ly' = Aasinat - Bacosat

На основе начальных условий имеем:

( 8 = 0,48А + 0,88 B

{-2 = 0,52 * 0,88A - 0,52 * 0,48 B

(-2 = 0,45A - 0,23B

{ 8 = 0,48A + 0,88B

(-4,44 =A- 0,5B {16,6 = A +1,83 B

21,04 = 0 + 2,33B

B=9

A=-4,44+0,5B=-4,44+4,5≈0 значит B=9; А=0. Из этого следует y=9cos 0,51t

Поэтому колебательный процесс имеет следующий вид: y = f(t)+E(t), где f(t) показывает общую тенденцию роста урожайности, а E(t) ̶ воздествие внешней среды (шум). В нашем случае Е (t) = Acos 2^ = 4,4cos^^; f(t)=0.0122t2 - 0.4328t+33,246 и поэтому y=0.0122t2 -0.4328t+33,246+9cos— .

, 12

Таблица 4. Сопоставление фактических и расчётных значений урожайности хлопчатника с учётом цикличности КОЛЕБАНИЙ .

Год	1991	1992	1993	1994	1995	1996	1997	1998	1999	2000	2001
Y ф	34,0	32,0	34,9	32,2	33,4	28,6	29,3	29,5	31,3	27,3	27,1
Yр	34,747	31,3	33,9	30,6	33,2	29,9	32,6	29,3	32,1	28,8	31,6
Y ф - Yр	-0,7	0,7	1,0	1,6	0,2	-1,3	-3,3	0,2	-0,8	-1,5	-4,5

Год	2002	2003	2004	2005	2006	2007	2008	2009	2010	2011
Y ф	28,2	29,3	30,6	30,9	29,4	30,3	25,8	28,6	31,0	32,6
Yр	28,5	31,3	28,2	31,1	28	30,9	27,9	30,9	27,9	31
Y ф - Yр	-0,3	-2,0	2,4	-0,2	1,4	-0,7	-2,1	-2,3	3,1	1,6

Год	2012	2013	2014	2015	2016	2017	2018	2019	2020	2021	2022	2023
Y ф	31,5	31,4	31,3	32,6	30,2	29,3	28,3	30,1	27,7	33,7	36,6	27,6
Yр	28	31,1	28,2	31,4	28,5	31,7	28,9	32,2	29,5	32,7	30	33,4
Y ф - Yр	3,5	0,3	3,1	1,2	1,7	-2,4	-0,6	-2,1	-1,8	1,0	6,6	-5,8

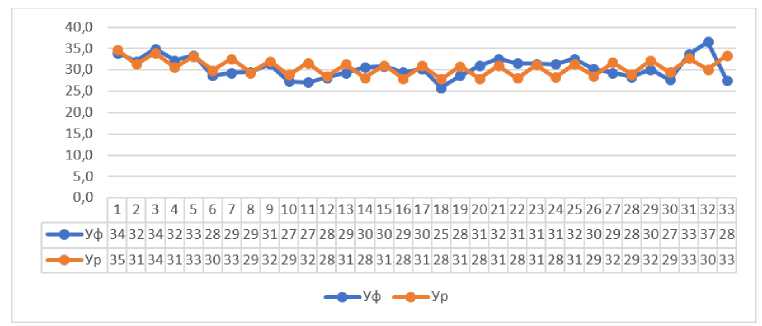
Рисунок 2. Графическое сопостовление фактических и расчетних значений урожайности хлопчатника в Бухарской области.

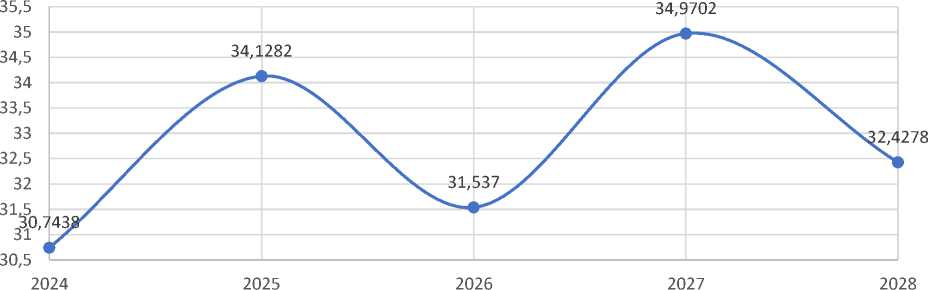
Рисунок 3. Графический прогноз урожайности хлопчатника с учётом колебаний.

Фактические и расчетные значения урожайности хлопчатника рассмотрены на графиках, представленных на рисунках 2 и 3.

Отсюда видно, что цикличность при прогнозировании обеспечивает надёжный результат.

ЗАКЛЮЧЕНИЕ

Таким образом в данной статье получены следующие результаты:

Если имеются экспериментальные данные, характеризующие состояние объекта в точках xi в виде yi, то можно определить, что этот процесс является гармоническим или не гармоническим. Необходимым условием гармоничности является: —^ /у = —а2 = ±A. Если, А > 0, то

△ %²

процесс является колебательным процессом.

Когда известно значение ш = 2^ , то автоматически определяется период колебания Т = — и частота колебания у = 1.

ш ⁷ Т

Если А < 0, то общим решением уравнения и искомой зависимости является гармоническая функция: у = Asin^ax + Bcos^wx.

При А>0 этот процесс не является гармоническим, а имеет следующий вид: у = Ae^x + Ве^-Х .

В любом случае коэффициенты А и В гармонической функции определяются на основе начальных условий y(x₀) = у₀ иу'(х₀) = у 0 . При этом решается система из двух уравнений с двумя неизвестными и определяются коэффициенты А и В.

Метод апробирован на основе конкретного примера, в результате которого получена пригодность излагаемого алгоритма для решения поставленной задачи.

Статья