Амплитудно-фазовое распределение для формирования частотно-независимых пеленгационных характеристик в линейных антенных решетках

Для ряда направлений применения антенных систем широкополосных радиоэлектронных комплексов требуется формирование частотно-независимых характеристик направленности и, в частности, частотно-независимых пеленгационных характеристик (ПХ). Формирование частотно-независимых ПХ позволяет значительно упростить построение широкополосных радиопеленгаторов [1–3], когда во всей полосе рабочих частот поддерживается постоянным пересечение парциальных диаграмм направленности (ДН) на уровне минус 3…4 дБ. Такая задача является актуальной для радиопеленгаторов с различными антенными системами, включая и линейные антенные решетки (АР).

Для определения частотной зависимости амплитудно-фазового распределения (АФР) в раскрыве АР, обеспечивающего формирование частотно-независимых ПХ, могут использоваться методы амплитудно-фазового синтеза [4–6]. Однако получаемые при этом решения приводят к сложным, зачастую нереализуемым АФР в раскрыве антенны. В то же время для практики актуальным является построение антенн, которые бы обеспечивали формирование частотно-независимых ПХ при неизменном от частоты амплитудном распределении в раскрыве линейной АР, а частотную зависимость имело бы только фазовое распределение.

Цель работы – изучить основные закономерности выбора параметров АФР для формирования частотно-независимых ПХ линейных АР при независимом от частоты амплитудном и изменяющемся с частотой фазовом распределении в раскрыве.

Результаты работ [1–3; 7] показывают, что эффект стабилизации ПХ линейного или прямоугольного раскрыва в широкой полосе частот ∆F непосредственно связан с формированием частотно-независимых парциальных ДН и может быть достигнут при выполнении следующих условий:

– в раскрыве должно быть сформировано независимое от частоты спадающее амплитудное распределение;

– должно быть введено соответствующее дополнительное частотно-зависимое четное (обычно квадратичное) фазовое распределение, при котором убывание ширины ДН с ростом частоты компенсируется возрастанием расфазировки раскрыва. Под расфазировкой раскрыва АР будем понимать величину разности фаз возбуждения центральных и крайних излучателей, задаваемых дополнительным фазовым распределением.

Однако как с теоретической, так и с практической точек зрения представляет интерес уточнение АФР, обеспечивающего частотную стабилизацию ПХ. При этом для исследования основных закономерностей, связанных с выбором АФР, как правило, достаточно рассмотреть случай линейных АР.

Рассмотрим линейную АР, геометрия которой показана на рис. 1.

Представим АФР линейной N -элементной АР длиной L следующим образом:

A (xn, f ) = to

= 2 ( ^Вт^ХПm ) exp { — i [ x n sin ° 0 + ^{АФ (} f ) ^ХП ] } ’ m = 0

yA

1     2     3 n n + 1 n + 2 N

Рис. 1. Геометрия линейной АР где Bm – частотно-независимые коэффициенты разложения, определяющие амплитудное распределение в линейной АР; xn е[-L2, L2] - координата n-го излучателя в линейной АР; АФ(f) -функция, определяющая частотную зависимость дополнительной расфазировки раскрыва; 9о -требуемое угловое положение главного максимума ДН.

Частотную зависимость расфазировки АФ ( f ) представим следующим соотношением

АФ ( f ) -l ⁵^ ( f — f , ) | Р .                  (2)

l ^{A F}              J

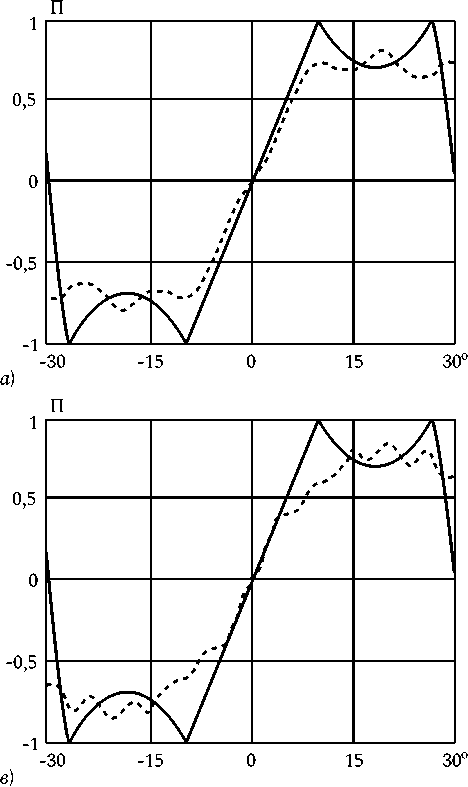
Рис. 2. Сравнение пеленгационных характеристик на частоте 2 f ^ ( а ); 3 f ^ ( б ) и 4 f ^ ( в ) с пеленгационной характеристикой на частоте f ^ (сплошная линия на полях а, б, в ) и частотная зависимость их отклонения в полосе частот ( г ) для амплитудного распределения с параметрами B ₀ = 0, Б ^ =-П21 4

в котором Ф о и Ф 1 - величина расфазировки раскрыва на крайних частотах f 3 и f 3 + A F соответственно. С учетом представления АФР в виде (1) соотношение для ДН решетки может быть записано в виде [4–6]

N да

F (0, f Ь(0)££( ВтхП m )х n=1 m=0                                 (3)

х exp{-i[k(f)xn (sin0- sin 00) + АФ(f)x2]|, где ц(0) — ДН излучателя; k(f) - волновое число.

На основе соотношения (3) ПХ линейной АР может быть представлена соотношением n ( 0 , f ) = ^F ^f ) — ^F j^ f ) .          (4)

'    ' F ( e+e „ , f ) + F ( e-e „ , f )

Параметром, определяющим частотную независимость ПХ, является интегральное среднеквадратическое отклонение (СКО) ПХ в полосе частот от ПХ на нижней частоте, которое определяется следующим выражением

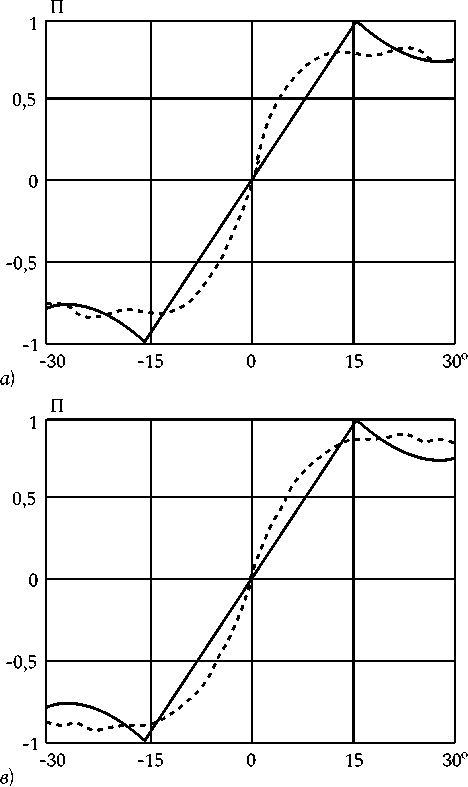
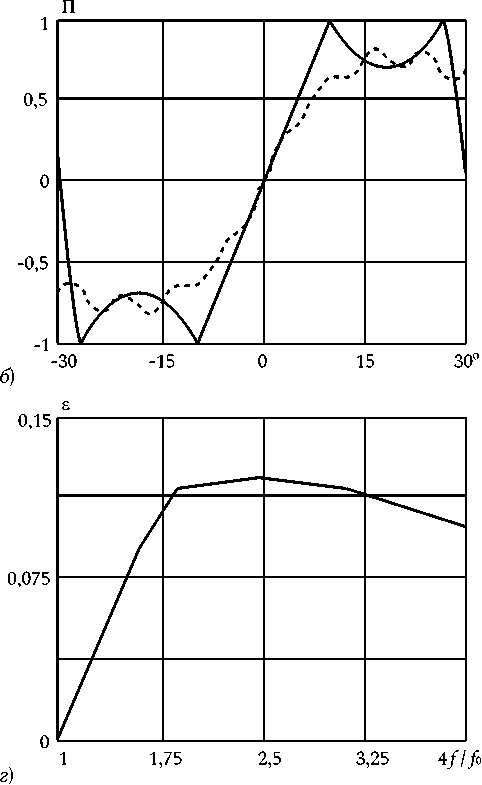
Рис. 3. Сравнение пеленгационных характеристик на частоте 2 f 3 ( а ); 3 f 3 ( б) и 4 f ₃ ( в ) с пеленгационной характеристикой на частоте f 3 (сплошная линия на полях а, б, в ) и частотная зависимость их отклонения в полосе частот ( г ) для амплитудного распределения с параметрами В о = 0, B i =-n²^ 2

Н^П ( ^{0 ,} f -Р)Г ( ^А f )^{- 1} I |^П ( ^{0 ,} f ) — ^П ( ^{0 ,} f =Р)| ² df . ^{(5) А f}

Результаты исследований возможности формирования частотно-независимой ПХ для 45-элементной АР в полосе частот с перекрытием 4:1 ( A F = 3 f о ) для различных параметров амплитудного распределения приведены на рис. 2 и 3, при этом частотная зависимость расфазировки взята в 0,8

виде АФ ( f ) = ( 3 л ( f/f 0 - 1 ) } .

На рис. 2 (поля с индексами а - в ) приведены расчетные ПХ для амплитудного распределения с параметрами В о = 0, B i = -п ²^4 с высоким уровнем возбуждения крайних излучателей АР. Сплошной линией показаны ПХ на частоте f ₀, штриховой линией - ПХ на частотах 2 f 3 , 3 f 3 и 4 f 3 соответственно. Из приведенных на рис. 2 зависимостей следует, что при повышении частоты происходит искажение ПХ. Однако максимальное в соответствии с выражением (5) искажение ПХ для этого

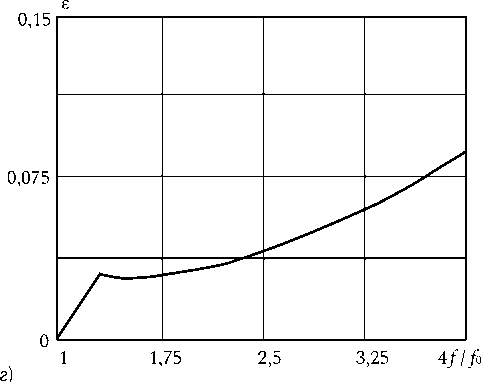
амплитудного распределения наблюдается вблизи середины полосы частот (рис. 2, г ).

На рис. 3 приведены результаты аналогичных исследований для случая существенно спадающего амплитудного распределения в раскрыве АР с параметрами B 0 = 0, B i = -л²/ 2. Переход к более спадающему амплитудному распределению позволяет, как следует из результатов, представленных на рис. 3, а – в при той же расфазировке в раскрыве АР снизить частотную зависимость ПХ. При этом характер частотной зависимости степени искажения ПХ, показанный на рис. 3, г существенно изменяется по сравнению с предыдущим случаем.

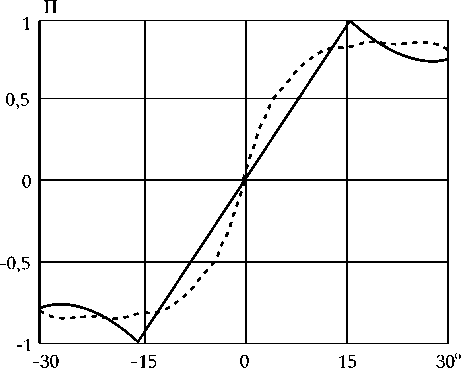
На рис. 4 для случая 45-элементной АР с амплитудным распределением B о = 0, B i = -л²/ 2 приведены результаты исследований изменения ПХ в полосе частот в зависимости от параметра p в выражении для частотной зависимости расфазировки раскрыва АР (2). Сплошной линией показаны ПХ на частоте f ₀, штриховой линией – ПХ на частоте 2 f ₀ , штрих-пунктирной линией – ПХ на частоте 3 f ₀, точками показаны ПХ на частоте 4 f ₀.

Приведенные на рис. 4 зависимости ПХ показывают, что при спадающем амплитудном распределении возможен выбор параметров частотно-зависимого фазового распределения в раскрыве АР, при котором в широкой полосе частот формируется практическая независимая ПХ.

Таким образом, можно отметить, что формирование частотно-независимых ПХ в широкой полосе частот возможно на основе следующих принципов:

– амплитудное распределение в раскрыве является частотно-независимым;

– изменение дополнительного фазового распределения в раскрыве АР от частоты имеет характер, близкий к линейному;

– частотная зависимость отклонения ПХ определяется параметрами амплитудного распределения, требования к которому могут обуславливаться различными факторами, при этом введение существенно спадающего амплитудного распределения способствует снижению интегрального СКО ПХ в полосе частот;

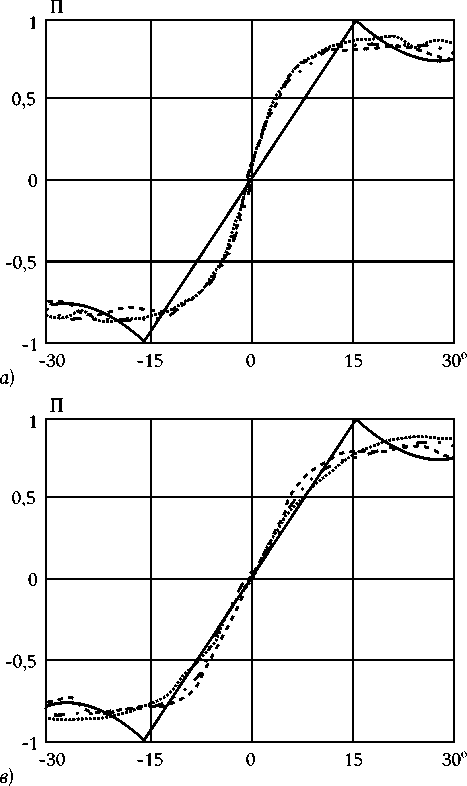
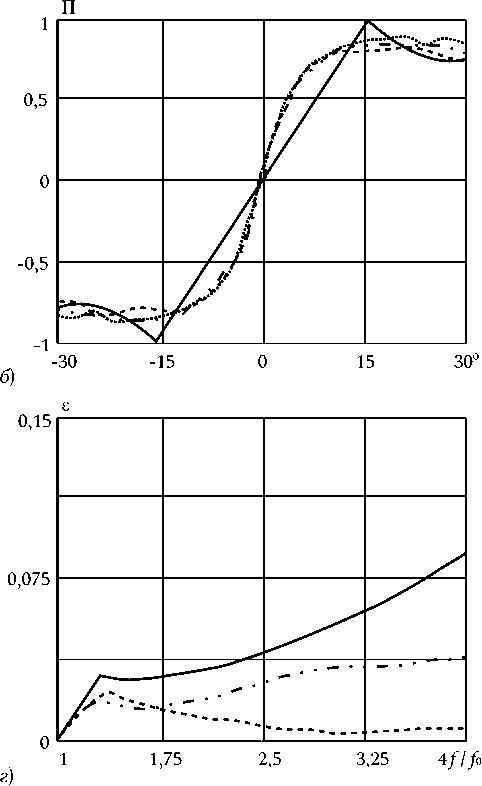
Рис. 4. Пеленгационные характеристики ( а - p = 0,8; б - p = 0,85; в - p = 0,9) и частотная зависимость их отклонения ( г ): сплошная линия p = 0,8; штриховая линия p = 0,85; штрих-пунктирная линия p = 0,9

– изменение закона расфазировки поля в рас- Учет выявленных закономерностей позволяет крыве решетки приводит к изменению характера  уточнить характеристики и сократить время раз- частотной зависимости отклонения ПХ.           работки частотно-независимых пеленгационных антенных решеток.