Амплитудно-инициируемая открытая петля гистерезиса затухания р-волны в песчанике: экспериментальное исследование

Введение и постановка проблемы

Новые фундаментальные знания в физике деформирования горных пород могут быть использованы для повышения геологической эффективности сейсмических и акустических методов исследования. Для этого требуется глубокое изучение механизма деформации при распространении и затухании упругих волн, который действует на микро/нано-уровне. Малоизвестное в геофизике свойство микропластичности горных пород может проявляться даже при малых деформациях. Сейсмические и акустические методы используют диапазон динамических малых и очень малых деформаций. Динамические процессы на больших и умеренных деформациях хорошо изучены. С появлением новых знаний о нелинейности интерес к области малых деформаций в сейсмике увеличился [1–6].

Следует отметить, что была предложена модель мезоскопической упругости (mesoscopic elasticity), которая объясняет механизм нелинейности горных пород. Новые инструменты, такие как нелинейная резонансная ультразвуковая спектроскопия, используются для выявления сложного поведения горных пород и других материалов. Имеются экспериментальные данные, что вязко-упруго-пластические модели наиболее реалистично отражают сложные деформации в горных породах по сравнению с традиционными моделями. Это существенное продвижение в расширении границ действия неупругих процессов и перспектива практического применения новых знаний [7, 8].

Теоретико-экспериментальные исследования в сейсмике и других областях физики твердого тела и материаловедения совершенствуют классическую вязкоупругую модель стандартного линейного тела, которая хорошо описывает дисперсию, релаксацию и связанные с нею неупругие процессы [9–12]. Экспериментальные результаты сравнивались с предсказаниями скорости волны и затухания, полученными с использованием модели Био (струйного течения) и других моделей. Однако эти модели не учитывают эффекта амплитудной зависимости скоростей волн и затухания, который обнаружен современными исследованиями [13, 14]. Лабораторные эксперименты на образцах твердых осадочных пород, извлеченных с больших глубин, подтверждают наличие амплитудного эффекта. Поведение динамических параметров сейсмических и акустических волн при распространении в различных средах является сложным и пока мало изучено.

С изменением величины амплитуды сигнала наблюдается как увеличение, так уменьшение скорости волны и затухания. Уменьшение или увеличение модуля упругости происходит в соответствии с кривизной соотношения напряжение–деформация. Такое нестандартное поведение различных твердых тел, в том числе и горного материала, обусловлено совместным действием упругой и микропластиче-ской деформации [15–19]. В статическом режиме напряжения на диаграмме «напряжение–деформация» эффект амплитуды деформации представлен в виде «стресс–плато» и «стресс–падение». В динамическом режиме (распространение волн) влияние амплитудного эффекта можно видеть на форме волны в виде кратковременных стресс–плато и падения. Микропластичность пород допускает такое нерегулярное кратковременное «включение» процесса пластичности с одновременным действием упругой деформации, чему имеются теоретические подтверждения [20, 21]. В этой статье представлены результаты исследования амплитудно-зависимого гистерезиса затухания продольной волны в песчанике.

2022;7(1):30–36

Методики исследования и фактический материал

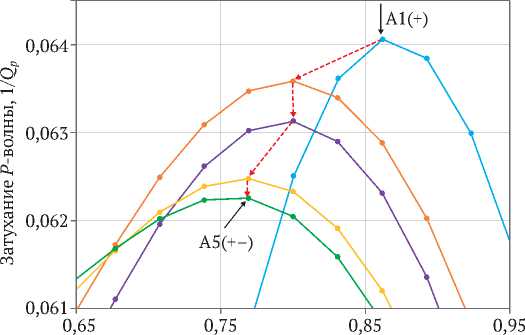
Частота, МГц

—•—A1(+) —•—A2(+) —•— A3(+) —•— A4(+) -•—A5(+–)

Рис. 1. Частотная зависимость затухания P -волны в песчанике на пяти восходящих значениях амплитуды деформации

Образец мелкозернистого песчаника изготовлен из керна, взятого с глубины 2532 м, плотность песчаника – 2,42 г/см³, содержание мелкозернистой песчаной фракции составляет 85 %, фракции алевролита – 15 %, общая пористость – 13 %. Эксперимент проводился при гидростатическом давлении 20 МПа при комнатной температуре. Образцы цилиндрической формы имеют следующие размеры: 40 мм в диаметре и 16 мм в длину. В эксперименте использовалась стандартная установка в виде трехслойной модели [22, 23]. Первый и третий слои обеспечивают идентичное отражение волны на границах раздела. Первый слой играет роль линии задержки, а третий слой – акустической нагрузки. Образец породы находится между этими слоями. Возбуждение и прием акустических сигналов обеспечивают пьезокерамические датчики на частоте ~ 1 МГц, которые поляризованы на продольную волну Декремент затухания 1/ Q_p вычисляется с использованием стандартных соотношений [24, 25]. Измерение декремента затухания волны проводилось в замкнутом амплитудном цикле на восходящем и нисходящем курсе, где A _min = A ₁ → A ₂ → … → A ₅ = A _max → … → A ₁ = A _min . На рисунках увеличение амплитуды помечено знаком ( + ), а ее уменьшение – (–). Величины относительной деформации амплитуд импульса следующие: ε 1 ≈ 0,5 × 10^–6, ε 2 ≈ 1,0 × 10^–6, ε 3 ≈ 1,3 × 10^–6, ε 4 ≈ 1,7 × 10^–6 и ε ₅ ≈ 2,0 × 10^–6. Скорость продольной волны в твердом песчанике составляет 4330 м/c. Повышение помехоустойчивости обеспечивает регистрация с накоплением сигнала.

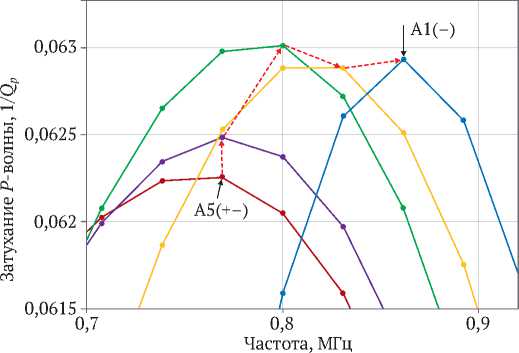
—•—A5(+–) —•— A5(–) —•—A3(–)   A2(–) -•—A1(–)

Рис. 2. Частотная зависимость затухания P -волны в песчанике на пяти нисходящих значениях амплитуды деформации

Результаты исследований

Частотная зависимость затухания Р -волны для восходящей и нисходящей амплитуд представлена соответственно на рис. 1 и 2. Затухание волны на всех амплитудах имеет вид релаксационного пика. С увеличением амплитуды сигнала величина затухания уменьшается, пик сдвигается в сторону низких частот, см. рис. 1. Нелинейный сдвиг пика затухания показан красными стрелками. На нисходящем амплитудном курсе величина затухания в пике слабо повышается, но не возвращается к исходному значению (красные стрелки на рис. 2). Амплитудная зависимость затухания продольной волны в песчанике на восходящих и нисходящих амплитудах деформации представлена на рис. 3. Здесь показана сравнительная картина поведения затухания волны для трех вариантов скорости волны. Во всех случаях затухание волны в зависимости от амплитуды деформации имеет форму петли гистерезиса открытого типа. Первый вариант имеет место в нашем эксперименте, где скорость волны для всех амплитуд постоянная – 4330 м/c. Остальные варианты – продукт простого моделирования. Второй вариант: линейное увеличение скорости волны на каждой амплитуде: А1(+) = 4350, 4360,4370,4380, А5(+) = 4390 м/с и затем обратное уменьшение по тем же величинам скорости, где (А1(-) = А1(+)). Третий вариант: линейное уменьшение скорости волны от А1(-) до А5(-) (4300, 4290, 4280, 4270, 4260 м/с) и обратное

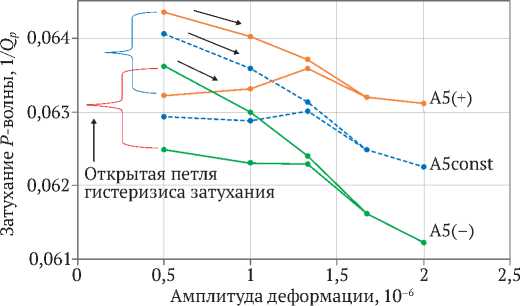
--♦-• –1/ Q p – V = const    —е— 1/ Q p модель V p (+)

—•— 1/ Q p модель V p (–)

Рис. 3. Зависимость затухания P -волны в песчанике от амплитуды деформации на восходящем и нисходящем курсе

2022;7(1):30–36

адекватное возвращение. Изменение величины скорости волны происходит в линейном режиме, которое не превышает величины 0,92 %. На максимальной амплитуде сигнала уменьшение затухания волны составляет: для постоянной скорости волны – 2,83 %, для возрастающей скорости – 1,93 % и на уменьшающейся скорости – 3,77 %. При постоянной скорости волны относительная величина незамкнутой части петли гистерезиса затухания составляет 62,63 %, при увеличении скорости волны – 91,58 % и при ее уменьшении – 47,01 %.

Фрагменты формы волны на амплитудах А1(+), А1(-) и А2(+), А2(-) в крупномасштабном отображении представлены на рис. 4. Это участок фронта волны, на котором можно видеть проявления нестандартного характера в виде микропластичности. Это – амплитудные плато, протяженность которых

составляет от одного до нескольких квантов времени t _квант , локальное падение амплитуды и эффект амплитудного микрогистерезиса. Максимум фронта волны на амплитудах А1(+), А1(-) и А2(+), А2(-) точно совпадают по времени 31,3425 мкс (красные стрелки на рис. 4). Минимум провала на фронте волны для тех же самых двух пар амплитуд располагается на одинаковом времени 31,765 мкс (красная штриховая линия на рис. 4). На фронте импульса присутствуют локальные петли амплитудного гистерезиса протяженностью в несколько квантов времени. Фрагменты формы волны на амплитудах А3(+), А3(-) и А4(+), А4(-) показаны на рис. 5. Здесь также присутствуют вышеописанные признаки микропластичности. Максимум и минимум в последней фазе импульса (31,3425 и 31,765 мкс) расположены на том же самом времени, что и в предыдущем случае.

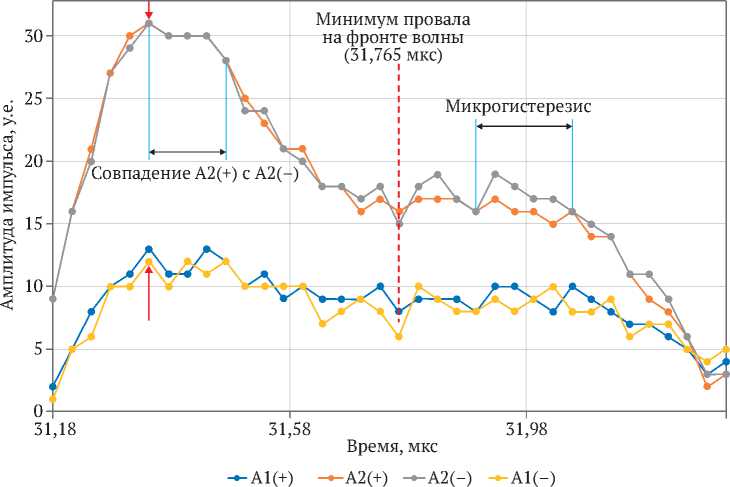
Рис. 4. Фрагменты формы волны на амплитудах A1(+-) и А2(+-) в крупномасштабном отображении

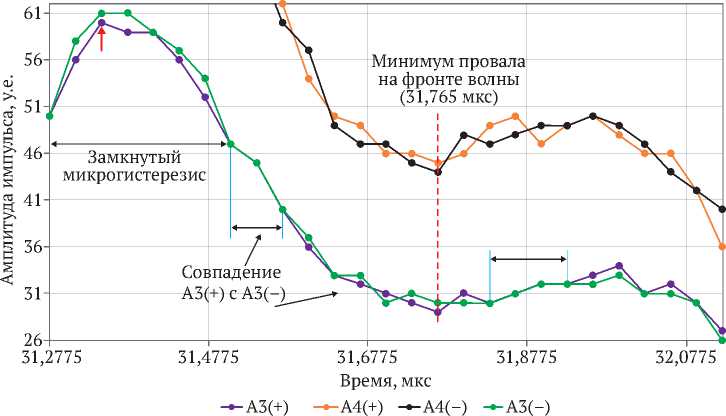
Рис. 5. Фрагменты формы волны на амплитудах A3(+-) и А4(+-) в крупномасштабном отображении

2022;7(1):30–36

Обсуждение результатов

Проведенное исследование показывает, что влияние амплитуды деформации и девиации скорости волны на параметры затухания волны в песчанике имеет необычный характер. При изменении величины амплитуды по замкнутому циклу кривая затухания волны 1/ Q_peak ( A_{n - i} ) имеет форму незамкнутого амплитудно-зависимого гистерезиса. Это требует пояснения механизма деформации в рамках физики деформирования горных пород и физики твердого тела. Незамкнутый гистерезис при распространении акустической P -волны указывает на возможность действия механизма нестандартной неупругости в песчанике. Наиболее вероятное объяснение этого эффекта дает механизм микропластичности горных пород. Микро-пластическая деформация сложным образом зависит от уровня деформации (величины прикладываемого механического воздействия). Затухание и скорость волны сложным образом зависят от уровня динамической деформации в песчанике. Малозначимое изменение (от 0,23 до 0,9 %) скорости продольной волны в амплитудном цикле вызывает более значительное изменение величины затухания – на 3 %. Новейшие исследования, проведенные на образцах горных пород с использованием высокоточной лазерной допплеровской интерферометрии, показывают, что изменение скорости волны за счет амплитуды достигает 5 % [26, 27].

Заключение

Анализ экспериментальных данных и пробное моделирование показывают сложный характер поведения затухания волны в зависимости от величины амплитуды и девиации скорости волны. В диапазоне частот 0,5–1,4 МГц затухание волны имеет форму релаксационного пика. Изменение величины амплитуды в замкнутом цикле (увеличение = уменьшение) приводит к сдвигу пика затухания в координатах «затухание –частота». Максимальное изменение величины затухания в пике за счет амплитудного фактора (в диапазоне деформации (0,5–2,0)10-6) достигает 3 %. Совместное действие амплитудного фактора и небольшого отклонения скорости волны (в диапазоне от 0,23 до 0,93 %) приводит к увеличению затухания в пике до ~ 4 %. Обнаруженная в эксперименте открытая петля гистерезиса затухания волны имеет место как при постоянной скорости волны, так и при переменной (амплитудно-зависимой) скорости. Относительная величина открытого гистерезиса существенно зависит от величины амплитуды деформации и девиации скорости волны. Проявления микропластичности, зарегистрированные в эксперименте, могут быть расценены как причина эффекта незамкнутого гистерезиса затухания волны в песчанике.

2022;7(1):30–36

2022;7(1):30–36