An analysis of the Avalos-Triggiani problem for the linear Oskolkov system of non-zero order and a system of wave equations

Let Q be a bounded domain in R n ,n = 2, 3, with sufficiently smooth boundary dQ. Let u = col(u 1 , u ₂ ,..., u n ) be a n— dimensional velocity vector n = 2, 3 , the scalar function p be a pressure, and the vector w = col(w 1 .w ₂ ,..., w _n ) be a vector of displacement of a body, which occupies the domain Q s , and is immersed in a fluid occupying the domain Q f . Therefore, Q = Q s U Q f , Q s П Q f = dQ s = r s is the common boundary of Q s , and Q f . Let us denote the outer boundary of Q f by r f (see Fig).

Our goal is to investigate the Avalos–Triggiani problem [1, 2] for the case when the fluid in Q f is an incompressible viscoelastic Kelvin-Voigt fluid of the nonzero-order [3]. The considered mathematical model is determined by the system

K

(1 — kV ² )u _t — ^ V ² u — ^ e l V ² w l + V p = 0    V (t, x) G (0, T] x Q f = Q Tf ,   (1)

l=1

∂wl —— = u + ai W1,   ai G R-, ∂t в1 G R+,    l = 1, K,    V(t,x) G QTf, (2) V • u = 0, V(t,x) G QTf, (3) wtt — V2w + w = 0 V(t, x) G (0, T] x Qs = Qts (4) with the boundary value conditions ulrf = 0,       V(t,x) G (0,T] x rf = rTf,                      (5)

w i | r f	= 0,        V (t, x) G r Tf ,	(6)
u = W t ,	V (t,x) G (0,T] x r s = r Ts ,	(7)

-      = p^{v      v (}t,^{x) e r} Ts                          (8)

and the initial value condition

(w(0, • ), W t (0, • ), w i (0, • ),..., w k (0, • ),u(0, • )) = (w o , w i , w io ,..., w k o ,u o ) e H , (9) where H = (H 1 (Q _s )) n x (L 2 (Q _s )) ⁿ x H 1 x ... x H _K x H f and H l = (L ² (Q _s )) ⁿ , l = TT" K, H f = { f e (L 2 (Q f )) ⁿ : V- f = 0 in Q f and [f • v] | r _f = 0 } .

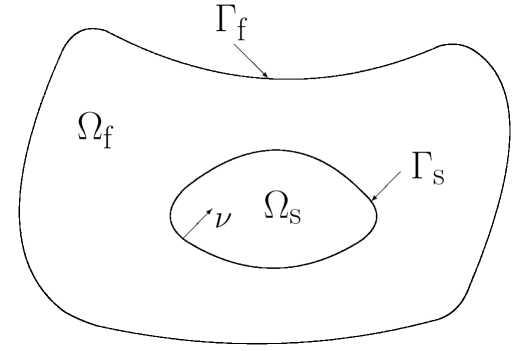
Fig. Physical model

In system (1), the parameters κ and µ characterize the elastic and viscous properties of the fluid, respectively, the parameters e l , l = 1, K determine the time of pressure retardation (delay), v is a unit normal vector. In the case of K = 0, к = 0 , problem (1) -(8) was investigated in [1,2], and for K = 0, к = 0 in [4], [5]. The case of K = 0, к = 0 is investigated for the first time.

1. Reduction to the Cauchy Problem

Following [1,2], we assume that p(t) satisfies the following elliptic problem:

Ap = 0 in QTf, ∂u ∂w p = dV •v - dV •v on Гт',                        (10)

∂p

— = Au • v   on   r _Tf .

∂ν

Then the pressure p can be represented as follows:

p^(t) = D s ^{{ (d}dVt⁾ • ^v - ^dwVt⁾ • ^v) _r ^{} +} N f ^((Au(t) • ^v) r _Tf )    ^{in    Q} Tf ;

where the Dirichlet map D s is defined by the relations

f Ah = 0 in Qf, h = Ds(g) О < h= ∂h g on rs, =0 on rf, ∂ν and the Neumann map Nf is defined by the relations

	f Ah = 0	in	Q f ,
h = N f (g ) ^ s	h =0 ∂h	on	r s ,
	< dV = g	on	r f

Then original system (1) – (4), which describes the interaction of the fluid and the body immersed in the fluid, takes the form

K

(1 - KV2)ut - ^V2u - ^ в1 V2wi - G1W - G2U = 0   V(t,x) G ^Tf,(11)

l =1

dW = u + aiwi,   ai G R-,   в1 G R+,   l = 1?X

V- u = 0, wtt - V2w + w = 0 V(t, x) G QTs(14)

with the boundary value conditions u|rf = 0, V(t,x) G Гт,, wl Ipf = 0       V(t,x) G rTf, u = Wt,       V(t,x) G rTs, where

G i w = V{D s { ( 5^ • v) _r }} in   Q t, ,

G 2 u = -V{ D s { ( ^ddtl • v) _r^ } + N , ((^u(t) • v) _F Tf ) }    in    П т, .

Let us rewrite the problem (11) – (17), in which pressure is excluded, in the form of an abstract Cauchy problem:

Lv) = Mv, v(0) = v ₀ , where the operators L and M are defined by the matrices

I		O	O	O	... O	O
	O	I	O	O	... O	O
	O	O	I	O	... O	O
L :=	O .	O .	O .	I .	... O ..	O .
	. . O	. . O	. . O	. . O	.. .. ... I	. . O
	O	O	O	O	... O	A κ	/

	O	I	O	O	... O	O
M : =	A - O O .	IO O O .	O α 1 O .	O O α 2 .	... O ... O ... O ..	O I I .	.
Here v = col(w, w t , w 1 , is clear out of the conte	.      ..      .     .      .         . .                       .                   .                        .                         ..                                   . O   O   O    O   . . .  α K       I G i    O e i A в 2 А ... в к A vA + G 2 ) w 2 ,..., w K , u), A K = 1 — kV 2 , I is a unit op xt. We study the problem (18) using the results						erator. Its domain obtained in [6–9].

Lemma 1. Let к E R , ^ E R + , the operators L and M be linear continuous operators from G to H ( L,M E L( G , H ) ), then there exists L ^{- 1} E L( H ). Here the space G = (H 2 (^ _s )) n x (H 2 (Q s )) n x9 1 x ... x9 K x9 _f , where 9 l = (H 2M )) n , l = TT K 9 _f is closure according to the norm of the space (H 2 (fi s )) n that is the space of infinitely differentiable solenoidal functions such that (15) – (17) are fulfilled.

Theorem 1. For any к E R, ^ E R + and v ₀ E G , there is the unique solution to the problem (18) v E C ^ ((0,T ], G )

In conclusion, we note that we intend to develop our research in the direction indicated in [10–12].

Acknowledgements. The work was carried out within the framework of solving problems for the development of the laboratory of Differential Equations and Mathematical Physics of Yaroslav-the-Wise Novgorod State University. The authors express their gratitude to Professor G.A. Sviridyuk for his attention to the work and discussion of the results.