An Analysis of the Effect of Communication for Multi-agent Planning in a Grid World Domain

Published Online May 2012 in MECS DOI: 10.5815/ijisa.2012.05.02

Research in multi-agent systems have led to its applicability in varied real world scenarios such as ecommerce [1], supply chain management [2], robotics [3], and also developing complex game application [4].It is widely being advocated for use in networking and mobile technologies, to achieve automatic and dynamic load balancing, high scalability, and self-healing networks. Such systems are becoming increasingly important as they draw together a number of important trends in modern technology [5].

A multi-agent system (MAS) consists of a collection of loosely-coupled interacting autonomous agents working in an environment. Here agents are usually software agents and can perform actions, have some computational abilities, and may communicate with each other. Multi-agent systems support modularization i.e., a large complex problem is handled by developing a number of functionally specific and

• II.    Agent Communication

The information exchange between agents is termed as communication between agents. Communication improves the behavior of agents and discourages any regard to other agent’s internal structure. The communication between agents may be peer to peer, broadcast or mediated. In recent years several techniques evolved for the communication between agents. Some of these include Blackboard system [8], message passing via communication standards like knowledge query manipulation language (KQML) [9], and FIPA-ACL [10]. Blackboard system is an indirect approach of communication between agents. In this technique there is a common blackboard which is shared between all agents. For peer to peer communication KQML and FIPA-ACL are two most popular languages. Since these languages are wrapper languages and have high level of abstraction they can be extended depending on the need of particular system [11]. Therefore in most of cases either these languages are extended according to need of application or engineers develop communication techniques suited for a particular application. In this paper we used a shared variable for agent communication. In our work the agents are collaborative in nature.

Figure1. Conceptual model for communication

• A.    Grid World Domain

In our work we used a two dimensional grid world domain that consists of cells arranged in a matrix. Some cells may be obstacles, represented by gray color in the figure shown below.

The size of the grid is 6X6. Cell that are darken in the figure are obstacles. No cell can be occupied by two or more agents simultaneously. Since in a multi-agent system the knowledge of an agent is limited and restricted to only local information, it only knows the information of its adjacent cells. The task of an agent is to reach the given goal state.

In this domain an agent can perform 4 actions, namely MOVE_LEFT, MOVE_RIGHT, MOVE_UP, and MOVE_DOWN. For example, after performing the action MOVE_DOWN, the agent moves one cell below the current cell. When all agents achieve their goal state then we says that the multi-agent system has achieved the goal, otherwise it is said to be failure.

• III .Architecture used for Communication

Communication is done using a shared variable. When an agent takes an action it updates its information in shared variable (communication module) and the other agent may retrieve the information from the communication module. The architecture of overall simulation system is shown below. The architecture of system consists of the following modules.

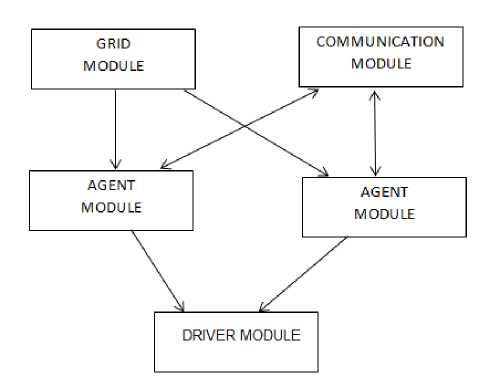
Figure3. Architecture of simulation system

• A.    Grid module

This module is used to design the grid world system on to which the multi-agent system is simulated.

• B.    Communication module

This module is used for communication between agents. In this communication module the agents share the information through the share variable. Agent interacts indirectly via the shared variable by broadcasting their current state.

• C.    Agent module

This module is used to describe the actions of the agents.

• D.    Driver module

This is used to run the program.

• IV .Theoretical Framework

A. Notations i, j: agents sj,curr: the current state of agent j sj, next: the next state of agent j

P: probability

Given the current state of the agents, the probability that the agents move to the next states is given as:

Z i,j(without-info-sharing) = P([s i,next , s j, next ] | [ s i,curr , s j,curr ])

= P(s_i,next | s_i,curr) . P(s j _{, next} | s j _,curr )    (1)

Since i and j are acting independently (i.e., there is no information sharing).

Theorem 1. Z i,j(with-info-sharing)

≥ Z i,j(without-info-sharing )

Proof: Consider a term t in Z i,j(with-info-sharing) and the corresponding term t ^′ in Z i,j(without-info-sharing) . Since the agents are communicating so P(s i,next | s i,curr ).

P(s j _{, next} | s j _,curr ) is more. Thus t ≥ t ^′ . Now Z_i j is the product of all the terms.

Since each term t ≥ t ^′ , so the product of the term in communication is also greater then equal to the product of term without communication. Hence the result.

We illustrate the above result by taking an example of the grid world structure in figure 2.

Let the initial position of agent i and j be (0, 2) and (2, 0) respectively. The final positions of the agents i and j are (4, 2), (2, 4) respectively.

Now, without information sharing between agents in the given grid world domain of figure 2, we find the individual probability values as follows. The probability of agent i taking first step from the initial position is ½ since there is available only two choices. Similarly for all the other steps to the goal state the probability values are 1, 1/3, and 1. For the agent j the probability values are 1/3 , 1, 1/3, 1.

Thus,

Z i,j(without-info-sharing) = P(s i,next | s i,curr ) . P (s j, next | s j,curr ) at each step is 1/2x1/3, 1x1, 1/3x1/3, 1x1.

Now with information sharing the probability of agent i for each step will be ½, 1, ½, and 1. The probability of agent j for each step will be 1/3, 1,1,1.

Proof: let us denote the LHS by A and the RHS by B

Thus A = Π ∀j Π ∀i Z i j (with info sharing)

B = Π ∀j Π ∀i Z i j (without info sharing)

By Theorem 1

we have Zi,j (with-info-sharing) ≥ Z i,j(without-info-sharing)

Thus the product of the terms for Zi,j(with-info-sharing)  is more than that for Zi,j(without-info-sharing)

Hence A ≥ B

For the example considered, by substituting the vales obtained before, we get

A = Π ∀j Π ∀i Z i j (with info sharing)

= 1/6x1x1/9x1

= 1/54

B = Π ∀j Π ∀i Z i j (without info sharing)

= (1/6x1x1/2x1)

= 1/12

We can see that A ≥ B.

Theorem 3: Expected time of convergence with information sharing (E _inf_o-sharing ) ≤ Expected time of convergence without information sharing (E _without-inf_o-sharing ).

Proof: Let m be the number of steps (transitions) for convergence. Expected convergence time = search time × number of free cells. Now search time depends on the local information available. Moreover,

Search time (with information sharing) ≤ search time (without information sharing). Therefore, E info-sharing ≤ E without-info-sharing .

Thus,

Z i,j(with-info-sharing)   = P(s i,next | s i,curr ) . P (s j, next | s j,curr )

at each step is 1/2x1/3, 1x1, 1/2x1, 1x1. We can see that that the value of each term in this case is more than the corresponding term in the previous case. Thus,

Z i,j(with-info-sharing)   ≥ Z i,j(without-info-sharing) .

• B.    Definition

Chain Probability: let s1, s2,….,sr,sg be a sequence of states that an agent makes. Where s1 is the initial state and sg is the final (goal) state. We call the probability of moving from s1 to sg via the sequence as the chain probability, de noted as P(s1,s2,….,sr,sg ). Now,

P(s1,s2,….,sr,sg ) = P(s1) . P(s2|s1)………P(sg|sr)

Theorem 2. Chain probability (with sharing) ≥ chain probability (without sharing)

• V. Experiments And Results

The purpose of our experiments is to demonstrate the importance of communication in a multi-agent system. For this we used the grid world domain in which two agents are acting together to achieve their goal. The experiments were carried out on a 2.26 GHz Intel Pentium machine with 2 GB RAM. The programs are written in C++ and executed on Windows7. We used the convention of naming each cell of the grid as a coordinate starting from 0 to 6 from left to right and top to bottom.

Abbreviations:

IA:-Initial position of agent A.

IB:-Initial position of agent B.

FA:-Final position of agent A.

FB:-Final position of agent B.

N:-Number of steps taken by agent to move from IA to FA.

ET:-Time taken by CPU to perform the simulation (in milliseconds).

NA: - Number of steps taken by Agent A to reach the goal position.

NB: - Number of steps has taken by Agent B to reach the goal position.

N_max = maximum (NA, NB)

• A.    Single agent system without communication

For a single agent in the grid world domain the experimental results for the different initial-final states are given in Table 1 and figure 4.

TABLE1. EXPERIMENT RESULTS WITH DIFFERENT CASES

Sr. no.	IA	FA	N	ET
1	2,4	3,4	1	0.009
2	0,2	2,2	2	0.015
3	0,4	4,4	4	0.032
4	2,2	3,5	4	0.032
5	1,5	4,3	5	0.046
6	1,0	5,1	7	0.078
7	0,0	5,2	7	0.078
8	4,4	1,0	7	0.078
9	1,5	5,1	8	0.093
10	0,5	5,0	10	0.109

On performing this experiment the path chosen by agent is shown below. And no. of steps taken by agent is 10. And the average time taken by agent to reach up to desire state was 0.109 msec.

Similarly number of experiment is performed by taking different position [Initial state] and goal state of agent. Since there is only single agent and if there is certainly a path is available between initial position and final position then there is no need of implementing communication model.

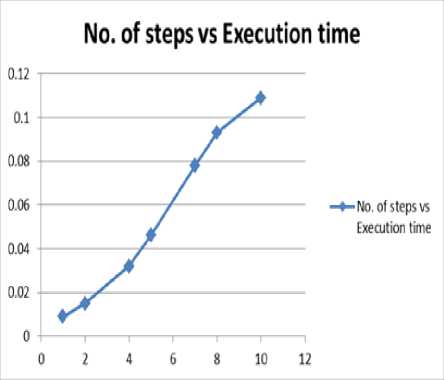
Figure4. No. of steps VS Execution time

• B.    Two agent system without communication

1) No U-turn is allowed

TABLE 2. TWO AGENT SYSTEM (no communication)

sr. no.	IA	FA	IB	FB	NA	NB	N-max	ET
1	2,4	3,4	2,2	4,2	1	2	2	0.047
2	0,2	2,2	0,4	3,4	2	3	3	0.063
3	0,4	4,4	0,0	2,3	4	5	5	0.109
4	1,0	5,1	0,5	5,5	5	7	7	0.172
5	0,0	5,5	0,5	5,0	10	10	10	0.234
6	0,0	5,0	0,2	5,2	5	5	5	0.108
7	2,2	4,5	0,1	5,2	5	6	6	0.136
8	2,0	5,0	0,0	5,5	3	10	10	0.234
9	3,2	4,5	2,3	4,2	4	3	4	0.084
10	4,0	2,2	0,4	4,4	4	4	4	0.087

For two agents in the grid world domain the experimental results for the different initial-final states are given in Table 2 and figures 5, 6.

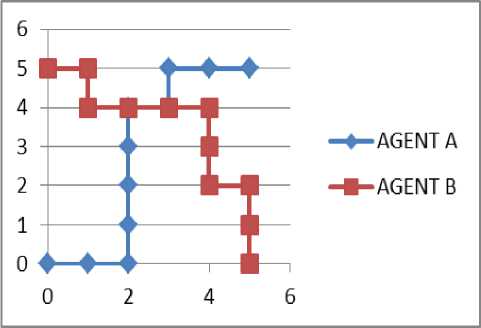
Figure5. A graph representation of movement of agent A and Agent B

we find that A has achieved its goal state but B has got stuck at the cell (5, 5).

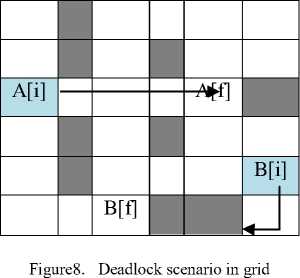
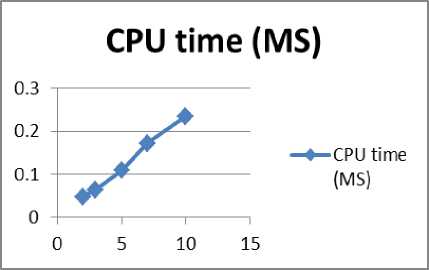
Figure6. No. of steps VS CPU time(ms)

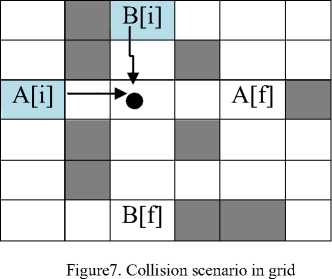
• a) Collision

We have observed that some situations there are collision of the agents. For instance, suppose that the agents are at initial positions (0, 2) and (2, 0); the corresponding final states of the agents are (4, 2) and (2, 4). This is shown in figure 7.

• 2)    U-turn is allowed

We have found that in this case deadlock cannot arise. However collision may still occur. An example situation is shown in the figure where the agent A now being able to take an U-turn prevents the deadlock.

The following Table 3 corresponds to situations where deadlock occurs. Table 4 corresponds to situations where no deadlock occurs.

b) Deadlock

There may be the possibility of a deadlock. This arises when any one agent get stuck somewhere, unable to make any further move, even though the other agent has achieved its goal. For instance, suppose that the initial position of agent A and B are (0, 0) and (4, 5) respectively and the goal state of the agents A and B are (5, 0) and (5, 2) respectively. At some point of execution

TABLE3. EXPERIMENTS AND RESULTS WITH DIFFERENT CASES FOR TWO AGENT SYSTEM

Sr no.	Agent A (initial position),(final position)	Agent B (initial position),(final position)	No. of steps taken (without U turn)	Result
1.	(1,0),(0,2)	(0,5),(5,0)	2	Agent A blocked
2.	(0,0),(4,4)	(4,5),(5,2)	1	Agent B blocked
3.	(1,0),(5,0)	(5,0),(0,0)	2	Agent A & B blocked
4.	(0,3),(3,0)	(2,2),(0,3)	1	Agent A&B blocked

• a)    Results with U-turn

TABLE4. EXPERIMENTS AND RESULTS WITH DIFFERENT CASES FOR TWO AGENT SYSTEM (with U-turn)

Sr no.	Agent A (initial position) ,(final position)	Agent B (initial position) ,(final position)	No. of steps taken (with U turn)	Min No. of steps need ed	Exec ution time	Result
1.	(1,0), (0,2)	(0,5), (5,0)	10	10	0.245	successful
2.	(0,0), (5,0)	(4,5), (5,2)	6	5	0.162	successful
3.	(2,0), (5,0)	(5,0), (0,0)	10	5	0.251	successful
4.	(0,3), (3,0)	(2,2), (0,3)	10	6	0.248	successful
5.	(2,4), (3,4)	(2,2), (4,2)	2	2	0.062	Successful
6.	(1,0), (5,1)	(0,5), (5,5)	7	7	0.184	Successful
7.	(2,2), (4,5)	(0,1), (5,2)	6	6	0.158	Successful
8.	(3,2), (4,5)	(2,3), (4,2)	5	5	0.124	Successful
9.	(4,0), (2,2)	(0,4), (4,4)	4	4	0.103	Successful
10.	(0,0), (5,5)	(0,5), (5,0)	10	10	0.252	Successful
11.	(0,2), (4,2)	(2,0), (2,4)	-	-	-	Collision

• b)    Analysis of result:

The above results can be summarized in Table 5.

TABLE5. ANALYSIS OF RESULTS

	COLLSION	DEADLOCK
Without Communication (no U turn )	Yes	Yes
Without Communication (U turn )	Yes	No

• C.    Two agent system with communication model

In a two agent system with communication, each agent communicates their current position and the next position that will arise for some action. Here next position indicates the intention of the agent to move to this position but it does not mean that the agent has actually moved to this position.

Before taking an action every agents will check the “other’s next position”. If the “other’s next position” is the same as “its next position” then they will look at a signal variable. Otherwise it takes the action according to local information available.

The purpose of the signal variable is to give a signal to the agents so that they can cross without any collision. The variable is a tuple (a, b) that can either be (1, 0) or (0, 1). For instance, (1, 0) means agent A is waiting; (0, 1) means agent B is waiting.

After taking the actions, the agents update the shared variable indicating the current position and next position.

In Table 6 the experimental results with communication are given. Now with communication there cannot be deadlock or collision. This is summarized in Table 7.

TABLE6. TWO AGENTS WITH COMMUNICATION

Sr. no.	IA	FA	IB	FB	N	ET
1	2,0	2,4	0,2	4,2	5	0.133
2	2,1	3,5	0,5	4,4	6	0.167
3.	0,4	4,4	0,0	2,3	5	0.141
4	1,0	5,1	0,5	5,5	7	0.186
5	0,0	5,5	0,5	5,0	10	0.264
6	0,0	5,0	0,2	5,2	5	0.137
7	2,2	4,5	0,1	5,2	6	0.158
8	2,0	5,0	0,0	5,5	10	0.265
9	3,2	4,5	2,3	4,2	5	0.138
10	4,0	2,2	0,4	4,4	4	0.118

Consider row 1 of Table 7. This result suggests that now with communication there is no collision; previously when there was no communication, collision occurred (refer to the last row of Table 4).

TABLE7. ANALYSIS OF RESULTS

	COLLSION	DEADLOCK
Without Communication (U turn)	Yes	No
Using communication	No	No

VI.Related Work

In this section we briefly report some works in a grid world domain for multi-agent planning. A continual planning technique is developed and implemented for the grid world in [12]. Our method is not based on continual planning.

Another similar domain based on a grid world is the packet world environment—that consists of a number of agents, packets, and baskets occupying different cells of a grid. The task of the agents is to cooperate among each other to pick up the packets and place them in the

Baskets In [13] a cooperative multi-agent system for solving the packet world problem is proposed.

In [14] Packet-World domain is considered. It consists of a number of differently colored packets that are scattered over a rectangular grid. The task of the agents is to cooperate among themselves to place these packets in the corresponding colored destination (cell). Architecture for such a multi-agent setting is suggested in [14].

• VII. Conclusion and Future work

In this paper we considered the problem of multiagent planning in a grid world domain. Our experimental results demonstrate the importance of communication in a multi-agent setting. As part of our future and ongoing work we would like to study similar grid world domains of different sizes and structures. We would also like to analyze the behavior of several agents in such domains.