An analysis of the Intelligent Predictive String Search Algorithm: A Probabilistic Approach
Автор: Dipendra Gurung, Udit Kr. Chakraborty, Pratikshya Sharma
Журнал: International Journal of Information Technology and Computer Science(IJITCS) @ijitcs
Статья в выпуске: 2 Vol. 9, 2017 года.
Бесплатный доступ
Due to the huge surge of digital information and the task of mining valuable information from huge amount of data, text processing tasks like string search has gained importance. Earlier techniques for text processing relied on following some predetermined sequence of steps or some hard coded rules. However, these techniques might soon prove to be inefficient as the amount of data generated by modern computer systems in increasing more and more. One solution to this problem lies in the development of intelligent algorithms that incorporate a certain degree of intelligence and unlike traditional algorithm are able to cope up with changing scenarios. This paper presents a string searching algorithm that incorporates a certain degree of intelligence to search for a string in a text. In the search of a string, the algorithm relies on a chance process and a certain probability at each step. An analysis of the algorithm based on the approach suggested by A. A. Markov is also presented in the paper. The expected number of average comparisons required for searching a string in a text is computed. Based on the varieties of applications that are coming up in the area of text processing and the related fields, this new algorithm aims to find its use.
String matching, Probabilistic analysis, Markov chain, State diagram
Короткий адрес: https://sciup.org/15012621
IDR: 15012621
Текст научной статьи An analysis of the Intelligent Predictive String Search Algorithm: A Probabilistic Approach
Published Online February 2017 in MECS DOI: 10.5815/ijitcs.2017.02.08
A lot of digital information is present in the form of text. This makes text processing tasks like string searching carry a lot of importance. It plays a significant role in a number of applications that include text editing, spell checking and correction. Moreover as a result of huge amount of information generated by modern systems and a similar volume of research data generated, the importance of tasks like string searching has only become two fold. Some recent areas in which string searching is important include sentiment analysis, text summarization and information retrieval systems. It also has a lot of significance in the areas of bioinformatics and bigdata.
A string search algorithm takes a text and a pattern, as the inputs and finds the first or all the occurrences of the pattern. Throughout this paper T is a text of length n and P is a pattern of length m such that m << n.
The most fundamental method of searching for a string in a text is to compare each character of the pattern and the text starting from the first and sliding the pattern by one position towards the right every time a mismatch occurs. This approach is known as the brute force method. Several other algorithms exist that have their own advantages and shortcomings based on the type of the text and the pattern. Some notable algorithms are the Boyer Moore algorithm, Horspool algorithm, KMP algorithm. Most of the algorithms work in two phases i.e. the pre-processing phase and the matching phase. During the pre-processing phase the pattern is processed and the data gained is used in the matching phase to shift the pattern in case of a mismatch.
The mentioned algorithms and their refinements have been use in systems and some have proven to be particularly efficient. However, with the advent of high-throughput systems, biologists, physicists, scientists and other researchers are joining the big-data club, and are starting to grapple with massive data sets, encountering challenges with extracting meaningful information and handling, processing and storing them. Although all the information eventually comes down to a collection of text, it is the variety and the amount of information that might prove to a bottleneck for the existing algorithms, that rely on hard coded rules and predetermined steps.
Much of modern research in the computer science domain is being focused on the development of intelligent algorithms that employ intelligent decision making to solve problems more efficiently. This paper presents a string search algorithm that does not require pre-processing like the existing algorithms and incorporates a certain degree of intelligent decision making while searching for a string. The algorithm uses predictions based only on the features of the text and finds the first occurrence of a pattern in a text. The paper also presents an analysis of the algorithm. A simple probabilistic approach has been taken to analyse the performance of the algorithm. Several factors determine the performance of a string search algorithm; however in this paper only the number of character comparisons made is taken into consideration to analyse the performance.
During the search of a string, comparison of a character provides vital information in determining the next step, which may be a next comparison or a shift of the pattern based on a match or a mismatch, which in turn affects the overall performance of the algorithm. The total number of character comparisons made thus proves to be an effective metric in analysing the performance of a string search algorithm. The analysis is based on a Markov chain approach to determine the average number of flips of a coin required to obtain consecutive heads.
The rest of the paper is organized as follows. Section II presents a description of some of the existing string searching algorithm. Section III presents a description of the Intelligent Predictive String Search Algorithm. Section IV illustrates the algorithm with some examples. Section V describes probabilistic analysis and Markov chain. Section VI presents an analysis of the algorithm based on the Markov Chain approach and finally the paper is concluded in Section VII.
-
II. Related Work
-
A. Boyer Moore Algorithm
The Boyer Moore algorithm is considered to be an efficient algorithm and is extensively used. All the algorithms prior to it attempted to find a pattern in a string by examining the leftmost character. Boyer and Moore believed that more information could be gained by beginning the comparison from the end of the pattern instead of the beginning [12]. This information often allows the pattern to proceed in large jumps through the text being searched [1]. The algorithm uses the bad character heuristic and the good suffix heuristic to determine the pattern shift in case of mismatch of a pattern character.
During the matching phase if there is a mismatch between the text character T[i] and the pattern character P[j] and if T[i] does not occur anywhere else in the pattern, then the pattern can be shifted completely by m positions towards the right. If T[i] is present in the pattern then the pattern is shifted until an occurrence of T[i] in the pattern gets aligned with T[i] of the text. This is the bad character heuristic.
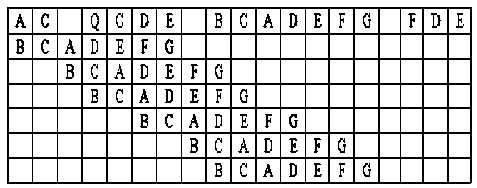
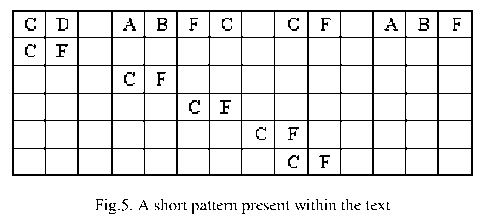
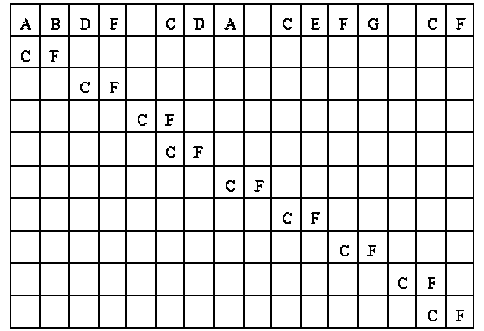
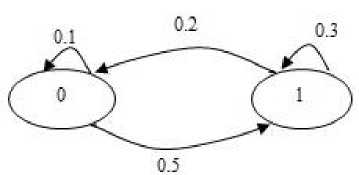
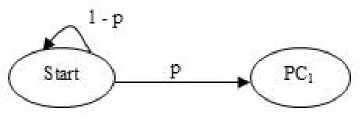
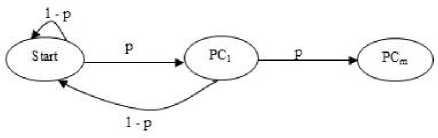
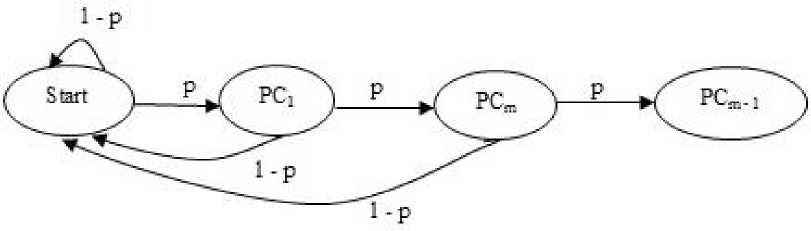
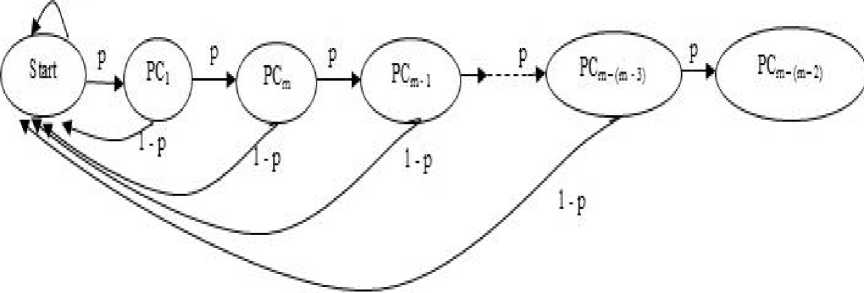
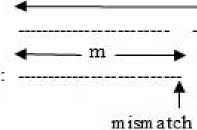
The second type of shift is guided by a successful match of the last k>0 characters of the pattern, P[j...m] and corresponding characters, T[i...(i+k)] of the text. P[j…m] is referred to as the suffix of size k of the pattern and is denoted as suff(k). If there is no occurrence of suff(k) in the pattern then it is shifted by its entire length. However if there exists a prefix (beginning part of the pattern) of size l The Boyer Moore algorithm has the property that the longer the pattern is, the faster it performs. However the algorithm suffers from the phenomenon that it tends to work inefficiently on small alphabets like DNA. The skip distance tends to stop growing with the pattern length because substrings re-occur frequently [15]. Also, the pre-processing for the good suffix heuristic is difficult to understand and implement [16]. Furthermore, it suffers from the need for very large tables or state machines and thus requires extra space [15]. It also requires extra time for processing the pattern. B. Horspool Algorithm The good suffix heuristic of the Boyer Moore algorithm is complicated and difficult to implement, Horspool suggested a refinement that uses only the bad character heuristic while achieving performance similar to that of the Boyer-Moore algorithm. The Boyer Moore algorithm uses the bad character of the text that caused a mismatch to determine the pattern shift distance. On the contrary Horspool’s bad character heuristic uses the rightmost character of the current text window. During the matching phase, if T[i] and P[j] do not match and T[l] is the rightmost character of the current text window then the pattern is inspected to find the rightmost occurrence of T[l] in it. If no occurrence of T[l] exists in P, the pattern is shifted completely by its length m, otherwise the pattern is shifted until T[l] gets aligned to its rightmost occurrence in P. Like the Boyer Moore algorithm, the Horspool algorithm gets faster for longer patterns. However as it uses only the bad character heuristic, it has a poorer worst case performance [17]. C. KMP Algorithm The Knuth Morris Pratt or the KMP algorithm begins the comparison from the leftmost character of the pattern. The following example explains the algorithm. 0 1 2 3 4 5 6 7 8 A В С А В С А В D A В С А В D А В С А В D Fig.1. KMP Algorithm [16] At the first attempt the characters through position 0-4 or the prefix ABCAB of the pattern have matched. Comparison C-D at position 5 yields a mismatch. In order to determine the shift of the pattern let us define the term border. A border of a string is a substring that is both proper prefix and proper suffix of the string. In the above example the border of the matching prefix ABCAB is AB. The width of the prefix and its border is 5 and 2 respectively. The shift distance is determined by the difference between the width of the matching prefix and its border, which is 3 [16]. The pattern is shifted by three positions towards the right. This shift aligns the pattern with its occurrence in the text. The KMP algorithm works efficiently on short patterns. However the performance of the KMP algorithm degrades for longer patterns as the possibility of character mismatch increases. As observed, all of the algorithms discussed rely on pre-processing the pattern and using the pre-computed values for searching a string. The predictive algorithm does not require pre-processing the pattern. It attempts to be more efficient and find application in areas in which the existing algorithms fail to perform. III. The Algorithm Let us consider that the leftmost characters of the pattern P and the text T are aligned. Also, let us make the assumption that the text consists of words separated by a blank space and the search is made for complete words and not their substrings. The following two observations can be made on examining the first character char1 of the text. If char1 is a blank space, then it is certain that the occurrence of pattern does not start at this position in the text. However the next position might be a possible beginning of the pattern. If char1 is different from the corresponding character of the pattern, then there are two possibilities. The next character might be another character of the same word or it might be a blank. If the first case arises then the pattern can be shifted by one position towards the right whereas if the second case arises the pattern can be shifted by two positions. Assuming the first character of the pattern match with that of the text, the mth character charm of the text is inspected. The following observations can be made. If charm is a blank space, it becomes certain that the pattern does not occur at the current alignment as clearly the text string is shorter than the pattern. If charm is different from the corresponding pattern character, then the next character of text is examined. The following lists the observations that can be made on examining the next text character. If the next character is a blank space, then the current word aligned is equal in length with the pattern and as charm is different from the corresponding pattern character, it is certain that the pattern does not occur at the current position. Hence it would be safe to slide the pattern by m positions towards the right. However, if the next character is not a blank space, a shift is made by two positions. As seen from the observations made, useful information can be gained by a simple examination of the text and using the same, the pattern shift distance can also be calculated. Base on the observations made earlier, two rules can be formulated to determine a shift of the pattern in case of a character mismatch. The two rules are named as the Alphabet-Blank mismatch rule and the AlphabetAlphabet mismatch rule. The algorithm has been designed to find the first occurrence of a pattern in a given text and as mentioned earlier the algorithm works in just a single phase i.e. the matching phase unlike other existing algorithms that work in two phases i.e. the preprocessing phase and the matching phase. Each character comparison is based on a chance process which may either lead to a match or mismatch. In case of a mismatch, the shift distance is predictively determined based on the type of mismatch. Fig.2. Schematic diagram for the algorithm Fig. 2. illustrates an instance of the algorithm. At the beginning, the leftmost ends of the text and the pattern are aligned. At each alignment of the pattern, the algorithm works on the portion of the text with size equal to the length of the pattern. This is known as the text window. The comparison starts with the leftmost character of the pattern and the text. If a match is found the rightmost character of the pattern is compared with the rightmost character of the current window. If this leads to a match, the remaining characters are compared from right to left. The two rules described earlier are applicable only when there is a mismatch of the leftmost or the rightmost character of the pattern. In case of mismatch at any other position the pattern is shifted by its entire length. The following describes the steps of the algorithm Algorithm_predictive_search(T,P) 1: Align T and P 2: Repeat steps 3 to 5 until a match is found or until the end of T is reached. 3: Compare P[0] and T[i] 4: if mismatch a: Alphabet-blank Re align P[0] to T[i+1] b: Alphabet-alphabet Re align P[0] to T[i+2] 5: if match compare P[m] to T[i+m] a: if match Compare remaining characters from right to left b: if mismatch 1: Alphabet-blank Re align P[0] to T[i+(m-1)+1] 2: Alphabet-alphabet a: if T[i+(m+1)] is blank Realign P[0] to T[i+(m-1)+2] b: else Realign P[0] to T[i+2] Line 4 handles a mismatch of the leftmost character of the pattern. If i is the position of mismatch in the text then in case of an alphabet-blank mismatch the leftmost character of the pattern is aligned to (i + 1)th character of the text and the (i + 2)th character in case of an alphabetalphabet mismatch. Line 5 handles a mismatch of the rightmost character of the pattern. In case of an alphabetblank mismatch, the pattern is shifted by its length to make an alignment with the (i + m)th character of the text. In case of an alphabet-alphabet mismatch, the next position is checked for a blank space. If it is a blank space, the pattern is shifted such that the leftmost character is aligned with the (i + m + 1)th character of the text, else the pattern is shifted to the (i + 2)th position. IV. Example The following examples illustrate the algorithm for different cases, namely, when the pattern is present at different locations in the text, for different lengths of the pattern and for different categories of mismatch. в в с А А В В с А А В в с А А В В с А А в В С А А В В С А А В Fig.3. Pattern search using the algorithm In the above example an average length pattern BCAAB is present at the end of the text. The algorithm directly begins with the matching by aligning the pattern BCAAB and the text. The leftmost comparison B-B yields a match. Hence the rightmost character of the pattern and the corresponding character of the current window are tried for a match. As this leads to an alphabet-blank mismatch, the pattern is shifted by its length. At the next alignment, the comparison A-B causes an alphabet-alphabet mismatch. As a result the pattern is shifted by two positions. The next comparison causes an alphabet-blank mismatch and thus a shift of one position is made. This shift aligns the pattern with its occurrence in the text as seen in the figure. The number of comparisons made is nine. The above example gives an insight into the average case performance of the algorithm as it illustrates the general cases of mismatch that occur during comparison of characters and the resulting pattern shift that take place. As seen from Fig. 3, an alphabet-blank mismatch is encountered at the rightmost position of the pattern and the resulting shift of the pattern made, which is one of the best possible shift. The example also shows an alphabetalphabet mismatch which is the most common type of mismatch that occurs. It also shows an alphabet-blank mismatch at the leftmost position which results in a shift of one position. The next example illustrates the performance of the algorithm when searching for a normal length pattern present within the text. Fig.4. An average length pattern present within the text The first comparison A-B leads to an alphabet-alphabet mismatch. As a result the pattern is shifted by two positions. The next causes an alphabet-blank mismatch and hence a shift of one position is made. The next comparison Q-B causes an alphabet-alphabet mismatch and so does the following comparison. The pattern is finally aligned with its occurrence in the text as a result of the shift made due to an alphabet-blank mismatch. The total number of comparisons made is twelve. In the example shown in Fig. 4, it can be observed that no more than shifts of two positions are made. This is because the leftmost comparison always leads to an alphabet-alphabet mismatch resulting in a shift of just two places. If such a situation arises then the algorithm enters its worst case. Moreover, the situation becomes even worse if the pattern is located at the end of the text or is not present at all. The next examples depict the performance of the algorithm for short length patterns present at different locations in the text. Experimental results have shown that the algorithm is able to achieve performance comparable to that of the Boyer Moore algorithm. Moreover, it is important to note that this performance is achieved without the pattern being preprocessed as in case of the Boyer Moore algorithm. Taking into consideration the text and the pattern used in Fig. 5, the following illustrates the performance of the Boyer Moore algorithm. In the above example a short pattern, CF is present within the text. The first comparison C-C leads to a match. Therefore the next comparison D-F is made. It causes an alphabet-alphabet mismatch and as it is the rightmost comparison, the next character of the text is inspected. Since it is a blank space, the pattern is shifted by its length plus one which brings it to the next alignment as shown in Fig. 5. The number of comparisons made up to this stage is two. The next comparison A-C causes an alphabet-alphabet mismatch and as a result the pattern is shifted by two positions. Similar is the case for the next comparison F-C. The following comparison causes an alphabet-blank mismatch and as it is the leftmost comparison, the pattern is shifted by one position. This shift aligns the pattern with its occurrence in the text. The total number of comparisons made is seven. In the following example the pattern CF is present at the end of the text. Fig.6. A short pattern present at the end of the text The first comparison A-C causes an alphabet-alphabet mismatch leading to a shift of two positions and so does the next comparison D-C. The next comparison causes an alphabet-blank mismatch causing a shift of one position. The next comparison C-C leads to a match whereas the next comparison D-F causes a mismatch, leading the pattern to be shifted by two positions. The next comparison A-C also results is a shift of two positions. The following comparison C-C leads to a match but the next comparison E-F causes a mismatch, which results in the pattern being shifted by its length. The next comparison F-C leads to a mismatch resulting in a shift of two positions. As the next comparison leads to an alphabet-blank mismatch a shift of one position is made. This shift aligns the pattern with its occurrence in the text. The total number of comparisons made is twelve. с D А В F С С F А В F с F С F С F С F С F Fig.7. Pattern search using Boyer Moore algorithm The first comparison D-F causes a mismatch. As D does not occur anywhere in the pattern, it is shifted by its length. The next comparison A-F also causes a mismatch and since A is not present in the pattern, it is shifted by its length. The next comparison F-F however causes a match. However the comparison of the preceding characters B-C causes a mismatch. As a result the pattern is shifted by its length. The next comparison causes a mismatch and as a blank space is not present in the text; the pattern is shifted by its length. This shift aligns the pattern with its occurrence in the text. The total number of comparisons made is seven. It was observed in Fig. 5, that the total number of comparisons made by the Predictive algorithm was also seven. It has been particularly observed that for shorter patterns the performance achieved by the Predictive algorithm is comparable to that of the Boyer Moore algorithm. The following table shows a comparison of the predictive algorithm with the Boyer Moore and the KMP algorithm. The comparisons are made on the basis of the number of character comparisons each algorithm makes for searching each word of the text A TEST OF THE PROPOSED ALGORITHM. Table 1. Comparison of the proposed algorithm with KMP and Boyer Moore algorithm Pattern Number of comparisons Boyer Moore KMP Intelligent Predictive A 1 1 1 TEST 5 6 5 OF 6 9 6 THE 7 15 10 PROPOSED 11 22 16 ALGORITHM 12 33 18 As seen from the table the Intelligent Predictive algorithm achieves performance comparable to that of the Boyer Moore algorithm and better than that of the KMP algorithm. V. Probabilistic Analysis and Markov Chain A probabilistic algorithm is an algorithm where the result or the way the result is obtained depends on chance. Some algorithms are by nature stochastic whereas in other cases the problem to be solved is deterministic but can be transformed into a stochastic one and solved by applying a probabilistic algorithm [14]. Probabilistic analysis is the use of probability in the analysis of problems [11]. A probabilistic analysis is performed using knowledge regarding the distribution of inputs or making assumptions regarding the same. Therefore, in the process averaging the performance over all possible inputs. Markov chain was introduced in 1906 by Andrei Andreyevich Markov. It is a stochastic and a type of a chance process in which the next step depends only on the current state. The steps preceding the current one do not have an impact on the next state. A Markov chain is characterized by a set of states and transition probabilities between the states. Markov chain can be formally defined as a sequence of n finite or countably finite trials. At each trial a probabilistic experiment is performed. The outcome of the experiment determines the state of the system at that time. The states are mutually exclusive, exhaustive and finite. Let X be an event that denotes the state of the system after each trial, then Xn = k, is an event that denotes the state k of the system at time n [1]. Xn is a random variable and has a probability distribution {ЯХ = Л).Л = О,1, 2,..}. (1) The Markov property states that the probability of moving to the next state depends only on the present states and not on the previous states. Р(Хп = л Xi = 1, X; = 2, X = 3..... Л**./ = п-1) = Р(Х, = н\Х^=П-1) In other words, the events X1 through Xn-2 have no influence on the event Xn. Only the event Xn-1 makes an influence on the event Xn. The system makes a transition from state i to j with the probability Pij = P(Xj = xj | Xi = xi ), known as the state transition probability. The transition probabilities form a transition probability matrix [5]. Given a transition matrix, Fig.8. Markov Chain Example A Markov chain for the same can be represented by a sequence of directed graphs where the edges are labeled by probabilities of transition from one state to another. VI. Analysis Given a text and a pattern, the problem of string searching is deterministic in nature as a string search algorithm will always make the same number of comparisons and will always produce the same result. In order to analyse its performance using the Markovian approach, the problem of string searching can be transformed into a stochastic one by making the following assumption. Let the comparison of pattern and text characters be an experiment € and X be an event such that the characters match. Let us suppose P(X) = p, then P(X’) = 1 – p, is the probability that a mismatch occurs. The sample space consists of sequences {x1, x2, …., xm} where each x is X or X’ depending on whether a match or mismatch occurred. For each alignment of the pattern, until a match is found, there will be k 2,;=л + m. The aim of the analysis is to determine the average number of comparisons that is needed to find the first occurrence of a pattern in a text. The matching phase begins by aligning the leftmost ends of the pattern and the text and comparing the characters for a match. The comparison stops only when all the characters of the pattern match with that of the text. A simple approach to determine the average number of comparisons required to find a match of the pattern can be made by assuming the problem of pattern matching to be similar to that of a coin tossing experiment of obtaining consecutive heads, each match denoting a head and a mismatch denoting a tail. The coin flipping experiment restarts each time a tail is obtained. Similarly, the algorithm realigns the pattern and restarts the comparison of characters of the pattern whenever a mismatch occurs. During the matching phase of the algorithm, if a match has occurred, then the next character is inspected for a match. Any prior mismatch will not cause the pattern to be shifted in this case nor does a prior match influence the next comparison. Similarly if a mismatch has occurred, the pattern is shifted based on the two shift rules and the matching restarts with the leftmost character of the pattern. No prior match will cause the next character to be inspected for a match nor will a previous mismatch have an influence on the shift of the pattern. Moreover, at each step during the matching phase a prediction is made and either a comparison or shift is made based on a certain probability. The comparison of characters of the text and the pattern form a chain of linked events which satisfy the Markov property. In the coin tossing experiment the average number of coin flips required to obtain consecutive heads is determined by first computing the average number of flips required to obtain one head. This result is then used to determine the same for two consecutive heads. Similarly, the result is used to obtain the value for three consecutive heads and so on and so forth. A similar approach is used to determine the average number of comparisons for finding a match of a pattern. The number of comparisons made would also depend on the features of the text like the frequency of occurrence of characters. However in this analysis the same has not been taken into consideration. Given a pattern of length m and a random text, this analysis tries to determine the performance of the algorithm in the worst possible case. A worst case arises when at each alignment of the pattern, (m – 1) characters of the pattern match whereas the last comparison causes a mismatch. Such a case would cause a large number of comparisons to be made if the pattern is located at the end of the text or is not present at all. To begin with the analysis the following assumption is made. Let the states of the Markov chain correspond to the characters of the pattern. For the ith pattern character, the state is denoted as PCi ( 1 ≤ i ≤ m ). Let C1 denote the average number of comparisons required to get a match of the first character of the pattern. Fig.9. Comparison of first character [13] As depicted in Fig. 9 above, if the comparison leads to a mismatch, which has the probability (1 – p), the pattern is shifted and the comparison is restarted. In this process, one comparison is wasted and the number of comparisons yet to be made is still C1. Thus, this gives (1 – p)(1 + C1), whereas if a match is found, the probability is p and the number of comparisons made is 1. This gives p.1. The expected number of comparisons is, Ci = (i-p)O + Ci)+p.i (5) On simplifying the above equation, i C1 = p On getting a match of the first character, the last character of the pattern is inspected for a match. The following figure depicts the comparisons. Fig.10. Comparison of the first and mth characters of the pattern [13] Let C2 denote the average number of comparisons required to find a match of the first and the last character of the pattern. As depicted in the Fig. 10, if this comparison leads to a mismatch, the pattern is shifted according to the shift rules and the comparison restarts and as a result two comparisons are wasted, one for the comparison of the last pattern character and the other for the first character, although the first comparison had led to a match. At this stage, the number of comparisons to be made is still C2. This gives p(1 – p)(2 + C2). On the other hand, if the last character matches, the goal is accomplished in two comparisons. This gives p2.2. Furthermore, if the first comparison is wasted on a mismatch, it will cause (1 – p)(1 + C2) to be added to the total number of comparisons to be made. The expected number of average comparisons is, Cl =(/-/>)(/ + C;) +p(l -p)(2 + Cj) + p1.2 (7) On simplifying the equation, C2 = Similarly C3, the expected number of average comparisons required to find the match of the first, mth and (m – 1)th characters can be determined. Fig. 11. depicts this case. Fig.11. Comparison of the first, mth and (m – 1)th characters [13] Lp Fig.12. Comparison of all characters of the pattern [13] C3 is represented by the following equation, Cj = (1 -p)(l + CjJ + p((l -p)(2 + Сз) + p20-p9g + c3)+p5 (9) On simplifying, C3 = A similar approach can be used to determine the average number of comparisons required to find a match of the pattern. Fig. 12 depicts the case. Cm, the average number of comparisons required to find a match of the pattern is, C™ = (1-p)d + Cm) +pG -p)G + Cm) + p^G -p) (3 + Cm) + .... + p^U-p)^ + Cm) + p"-m c m The result is, c m or Observation 1: Fig. 12 represents a possible worst case scenario in which all but the last character of the pattern match for every alignment of the pattern. Such a situation would rarely occur but in case it occurs and moreover if the pattern is present at the end of the text or not present at all, a large number of comparisons would be made. In fact, all the characters of the text would be scanned. The number of comparisons that would be made in this case is represented by (14). However, it is important to note that the above observation is without taking into consideration the length of the text because as mentioned earlier the analysis is based on the coin flipping experiment of obtaining consecutive heads. Also, the value of p depends on the frequency of occurrence of English characters, which varies with characters. It would also not be incorrect to state that Fig. 12 represents a possible average case in which the pattern is present somewhere within the text and less than (m – 1) characters of the text are scanned at every alignment of the pattern until a match is found. However (14) depicts the worst possible case and moreover it would not be possible to perform the average case analysis without considering the length of the text. Observation 2: Generally, given a text containing words separated by a blank space, the algorithm makes a skip of two places when an alphabet-alphabet mismatch occurs. Also in case the last character of the pattern coincides with a blank space, the pattern is shifted by its entire length. Hence on an average the number of comparisons made before an occurrence of a pattern is found would be approximately close to (n/2). The shift of one made due to an alphabetblank mismatch is compensated by a shift of m places when the last character of the pattern coincides with a blank space. Moreover, the number of blank spaces in any text is comparatively less than the number of characters. This also justifies the observation. Observation 3: The best case occurs when the rightmost character of the pattern collides with a blank space in the text every time. Fig. 13 depicts such a case. For every alignment the leftmost character of the pattern matches with the corresponding character of the text whereas the rightmost character coincides with a blank space. In such a case the pattern is shifted by m positions every time. As a result the number of comparisons made is close to (n/m). Text: Iм alignment n 2nd alignment: -------~ mismatch 3rd alignment: -------^ mismatch 4Л alignment: ------ Pattern match Fig.13. Best case of the algorithm VII. Conclusion This paper presented an algorithm that incorporates the concept of predictive decision making, which is new to string matching in comparison to other areas of computer science. As the algorithm is based on a chance process a simple probabilistic approach was taken to determine the number of character comparisons made in the worst possible case. A Markovian approach was followed as the mechanism of character comparisons satisfied the Markov property. It was also seen that the performance of the algorithm is comparable to that of the Boyer Moore algorithm particularly for shorter patterns and better than that of the Knuth Morris Pratt algorithm. However the analysis was done without taking into consideration the length of the text. As a result the analysis could not be extended to the average case of the algorithm. Elaborating on the concept of predictive decision making to enable search of substrings in a text and the probabilistic analysis of the algorithm in the average case has been left for further research.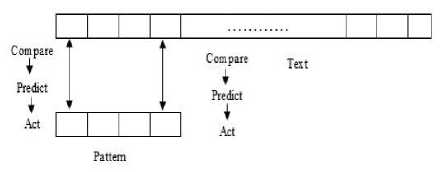
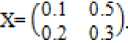
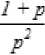
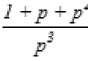
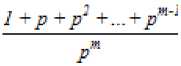
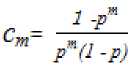
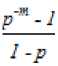
Список литературы An analysis of the Intelligent Predictive String Search Algorithm: A Probabilistic Approach
- Boyer, R. S.; Moore, J. S. A fast string searching algorithm. Commun. ACM 20, pp. 762-772, 1977.
- Donald E. Knuth, James H. Morris, Vaughan R. Pratt, Fast Pattern Matching In Strings in: Siam, Vol. 6, No. 2, pp. 323-350, June 1977.
- R. Nigel horspool, Practical fast searching in strings in: Software-Practice and Experience, vol. 10, pp. 501-506, 1980.
- Timo Raita, Tuning The Boyer-Moore-Horspool String Searching Algorithm in: Software-Practice And Experience, Vol. 22(10), pp. 879-884, October 1992.
- Gleb Gribakin, Probability and Distribution Theory, Chapter 4 Markov Chains, 110SOR201, 2002.
- Nimisha Singla, Deepak Garg, String Matching Algorithms and their Applicability in various Applications in: International Journal of Soft Computing and Engineering (IJSCE) ISSN: 2231-2307, Volume-I, Issue-6, pp.156-161, January 2012.
- Emma Haddi, Xiaohui Liu, Yong Shi, The Role of Text Pre-processing in Sentiment Analysis: International Conference on Information Technology and Quantitative Management, pp. 234-231, 2013.
- Vivien Marx, Biology: The big challenges of big data, Nature 498, doi:10.1038/498255a, pp. 255–260, June 2013.
- Dipendra Gurung, Udit Kr. Chakraborty, Pratikshya Sharma, Intelligent Predictive String Search algorithm: Proceedings of International Conference on Communication, Computing and Virtualization (ICCCV) 2016, Elsevier Procedia Computer Science, Volume 79, 2016, Pages 161–169.
- Olaronke G. Iroju, Janet O. Olaleke, "A Systematic Review of Natural Language Processing in Healthcare", I.J. Information Technology and Computer Science, 2015, 08, pp. 44-50.
- Anany Levitin: Introduction to The Design and Analysis of Algorithms, 2nd edition, ISBN: 9780321358288, published by Pearson Education, Inc., 2007.
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein, Introduction to Algorithms, third edition, MIT press.
- Suranga Hettiariachchi, Wesley Kerr: Boyer-Moore String Matching algorithm, Technical paper downloaded from http://cs.eou.edu/CSMM/surangah/research/boyer/boy.pdf
- https://www.cs.cornell.edu/~ginsparg/physics/info295/mh.pdf
- Probabilistic algorithms, Spring 2001 course, http://users.abo.fi/atorn/ProbAlg/Abstract.html
- http://www.cs.utexas.edu/~moore/best-ideas/string-searching/index.html
- http://www.inf.fh-flensburg.de/lang/algorithmen/pattern/ indexen.htm
- http://www.boost.org/doc/libs/1_54_0/libs/algorithm/doc/html/the_boost_algorithm_library/ Searching/BoyerMooreHorspool.html


