An Approach for Test Case Prioritization Based on Three Factors

Published Online March 2015 in MECS

The process of software testing is very important and necessary during the development of software. The main goal of software testing is to detect errors and to provide confidence that the software is free from errors. Software testing occurs in almost all phases of the software development life cycle (SDLC) such as from requirement phase to maintenance phase. In requirement gathering and analysis phase, software requirements are validated to ensure that they are feasible or not. In the design phase, software design is validated to ensure that it is built according to specification, in implementation phase software is tested to ensure that it performs its function according to intended software and so on. A variety of testing techniques are available to test the software product. Some techniques are used to check the overall functionalities of system, some are used to check the internal structure of the code. Regression testing is a type of software testing, aims to validate enhanced software, and it confirms that all the modifications done on software are correct. It occurs at maintenance level, and it is an expensive activity, yet it is necessary also. As the software evolves, there is a need to carry out regression testing, new test cases are generated and added to the test suite as a result of this regression testing’s cost rises. To re-execute all test cases of the entire test suite is the easiest and simplest strategy of regression testing, but due to certain constraints (time and resources), it is inefficient to implement this. For example, to execute all test cases of test suite for a product having approximately 20,000 lines of code, consumes seven weeks [1]. Therefore, it is necessary to discover the techniques with the goal of increasing the regression testing’s effectiveness, by arranging test cases of test suites according to some objective criteria.

The Test case prioritization techniques [2] intend to arrange test cases for regression testing in such a manner, with the goal of amplifying some criteria. Rothermel et al. [1] and Elbaum et al. [3] proposed a variety of test case prioritization techniques to the boost fault detection rate. Test case prioritization can address to boost a diversity of objective functions such as rate of fault detection, rate of detection of high-risk faults, likelihood of revealing regression errors, coverage of coverable code, and confidence in the reliability of the system under test [1]. Numerous techniques have been investigated to arrange test cases for regression testing, with an attempt to test modified software, nine different test case prioritization techniques have been explained by Rothermel et al. [1]. We have presented an approach for prioritizing regression test cases on the basis of three factors which are rate of fault detection (RFT), percentage of fault detected (PFD) and risk detection ability (RDA). RFT is defined as the average number of defects found per minute by a test case [6]. PFD is the percentage of fault detected by a test case. RDA is defined as the ability of test case to detect severe faults per unit time. For every test case all these three factors are computed, then test case ranking (TCR) is calculated for every test case by adding the value of these factors. For prioritization, we are scheduling the test cases in decreasing order of TCR value. And hence, we obtained the prioritized order of test cases. We have also compared our approach with other prioritization approaches and also with previous work [6] by calculating APFD for every technique.

The paper is organized as follows: section 2 discusses the related work, section 3 describes the proposed work, section 4 presents an experimental analysis, section 5 discusses the comparison of the proposed approach with other prioritization techniques and section 6 concludes the paper.

• II.    Related Work

This section discusses the test case prioritization problem as given by Elbaum et al. [3] and literature Survey.

• A.    Test Case Prioritization Problem

Test case prioritization intends to order test cases for regression testing in such a manner that test cases with higher priority executes earlier than those with lower priority, according to some performance criteria. The problem of Test Case Prioritization described in [3] as follows.

It is given that, T be the test suite, PT is the set of permutations of T and f is a function from PT to real numbers. The problem is to find T' which belongs to PT, such that, for every T", T" belongs to PT and (T" ≠T')

[f (T') ≥f (T")]

In the above definition, PT denotes the set of all possible prioritization or order of T, f is the function which is applied to any such order, and returns an award value for it.

• B.    Literatutre Survey

To maximize the regression testing’s effectiveness, researchers have investigated various metrics and techniques for prioritizing regression test cases, in recent years. Rothermel et al. [1], Elbaum et al. [3] and Malishevsky et al. [5] investigated various techniques for test case prioritization. Rothermel et al. [1] discussed numerous test case prioritization techniques and each technique was empirically evaluated for their ability to boost the rate of fault detection. It can be defined as how rapidly faults are found by test cases during the testing phase. The result of their study was that prioritization techniques can boost the rate of fault detection of test suite and this result also exists for a least expensive technique, the results reflects tradeoffs between various prioritization techniques.

Rothermel et al. [1] and Elbaum et al. [3] proposed a APFD (average percentage of fault detected) metric, for measuring fault detection rate as a means of objective criteria, prioritization techniques such as total statement coverage and additional statement coverage, function coverage, additional function coverage, FEP coverage have discussed to improve the rate of fault detection. APFD metric and these techniques consider that the costs of all test cases and defects severities are same. Elbaum et al. [4] and Malishevsky et al. [5] investigated a new metric APFD which includes fluctuating test case costs and fault severities into test case prioritization, to overcome APFD metric. Kavitha et al. [6] proposed a test case prioritization approach, which consider two factors: rate of fault detection (average number of defects found per minute by a test case) and fault impact. Testing efficacy could be progressed by emphasizing on test cases which detect greater percentage of severe faults. Thus, severity value was allocated to every fault depending on the fault’s impact on software.

Jeffrey and Gupta proposed an approach that used relevant slices to prioritize test cases [7]. Qu et al. [8] proposed an approach to prioritize test cases in black box environment. Korel et al. [9, 10] presented a model based technique that used information about the system model and its behavior for test case prioritization. Zhang et al [11] proposed technique based on changing priorities of testing requirements and test case costs to prioritize test cases. Kavitha et al. [14] proposed an approach for test case prioritization based on software requirement specification with the aim to increase the rate of detection of severe faults and to increase customer’s satisfaction by providing quality products. Their approach used three factors which are changes in requirement, customer’s priority and implementation complexity to prioritize test cases. Maheswari et al. [15] proposed a hamming distanced based approach to prioritized test cases. Faults revealed by test cases can be represented in binary form. For two strings with equal length, hamming distance can be defined as the number of positions at which corresponding symbols mismatched. Kayes [16] proposed a new metric and an approach for test case prioritization, the metric was used for evaluating rate of fault dependency. It can be defined as how rapidly dependency observed among faults. This new metric was used to determine the effectiveness of the proposed prioritized order and compare it with non prioritized order.

Various algorithms such as search algorithms and metaheuristic algorithms are also used to solve test case prioritization problem. Singh et al. [17] used ant colony optimization(ACO) algorithm to solve test case prioritization problem in a time constraint environment. ACO is an optimization algorithm that has been inspired from the behaviour of real ants while searching for food. The proposed approach was compared with other techniques by computing the average percentage of fault detected (APFD) for each. And it was concluded that APFD percentage of proposed techniques was equal to optimal ordering. Li et al [18] applied various algorithms such as greedy algorithm, additional greedy algorithm, 2-optimal algorithm, hill climbing and genetic algorithm to prioritize test cases and the results was that the genetic approach performed better.

Hla et al. [19] applied particle swarm optimization (PSO) algorithm to solve test case prioritization problem, by adjusting test cases to best position based on changes in software unit. PSO is a swarm intelligence based optimization algorithm, which search the best positions of objects from the search space. For the test case prioritization problem, the proposed algorithm finds the best positions of test cases on the basis of altered software parts, and prioritized test cases, according to new best order such that the test cases with higher new priority execute first. The conclusion drawn from the application of PSO algorithm to prioritize test cases was that it was effective and efficient to order test cases according to their new best positions. Li et al. [26] performed a simulation experiment to solve the problem of test case prioritization by applying five search algorithms, such as Total Greedy algorithm, 2- Optimal Greedy algorithm, additional Greedy algorithm, Hill Climbing, Genetic algorithm. They compared the performance of these algorithm, the goal of the study was to have detailed research or investigation, and to obtained generalized results.

Sabharwal et al. [20] presented an approach based on genetic algorithm for test case prioritization in the static testing environment. Mala et al. [21] used artificial bee colony optimization algorithm to prioritize test. They compared artificial bee colony optimization with ant colony optimization in test suite optimization and concluded that, artificial bee colony based approach has various advantages over an ant colony optimization based optimization. Huang et al. [22] proposed cost-cognizant approach to prioritized test cases on the basis of using historical data with genetic algorithm. Souza [25] designed a constrained PSO algorithm to solve the problem of test case selection. They considered requirement coverage and execution effort of test cases, the execution effort taken as a constraint in the search, and requirement coverage treated as fitness function. Binary Constrained PSO (BCPSO) and BCPSO integrated with forward selection (FS), BCPSO-FS were implemented, and both of these algorithm outperformed random search approach.

Sherriff et al. [23] proposed an approach for regression test case prioritization based on to figure out the impact of modification and by collecting software modification records and examining them through singular value decomposition. The approach produced clusters of files which tend to modify together historically and these clusters merged with test cases information that resulted in a matrix which was multiplied by a vector indicating a system change for test case prioritization. Alsmadi and Alda [24] proposed various approaches for test case selection to perform regression testing of web services. Test case selection aims to select a subset of test cases from test suite according to some performance criteria or some objective function. They suggested two proposals, the first is to build a pre-test execution component, which have the ability to evaluate generated test cases and optimize the selection for execution, from these generated test cases.

• III.    Proposed Approach

We proposed an approach to solve the test case prioritization problem based on three factors, which are rate of fault detection, percentage of fault detected and risk detection ability. For each of the test case in the test suite, all the three factors are calculated, then test case ranking is computed for every test case by adding these factors. For prioritization, test cases are arranged in decreasing order of test case ranking value. Test cases are arranged in such a way that those with greater test case ranking values executes earlier. Fig.1. represent the diagrammatic representation of the proposed approach. In this section the factors taken for prioritization and proposed prioritization technique are described.

• A.    Factors Taken For Proposed Approach

We consider three factors for proposed prioritization technique. These factors are discussed as follows.

• •    Rate of Fault Detection

The rate of fault detection (RFT) is defined as the average number of defects found per minute by a test case [6]. For test case T j , RFT j have been computed using number of defects found by T j and the time needed by T j to detect those defects. Kavitha et al. [6] express the equation as follows.

N

RFT j = —j— x 10 time _j

Where N j is Number of faults detected by test case T j and time j refers to the time taken by test case T j _.

• •    Percentage of Fault Detected

The percentage of fault detected (PFD) for test case T j can be computed by using number of faults found by test case T j and total number of faults, expressed as follows.

PFD

r N a

i N j

x 10

Where N j is the number of faults detected by test case T j and N refers to the total number of faults. To calculate percentage of fault detected, instead of multiplying by 100, we are multiplying by 10, to make the calculation easy.

• •    Risk Detection Ability

It can be defined as the ability of test case to detect severe faults per unit time. Testing efficacy could be progressed by emphasizing on test cases which detect greater percentage of severe faults. We presented an approach for prioritizing regression test cases by associating them with defect severity. The term severity is defined as time needed to pinpoint and rectify a fault, or the factors consider by practitioners are harm to persons or property, expense of ruined business and so on [4]. Thus, severity value was allocated to every fault depending on the fault’s impact on software. To every fault a severity value has been allocated based on a 10 point scale in [6] expressed as follows.

Very High Severe: SV of 10

High Severe: SV of 8

Medium Severe: SV of 6

Less Severe: SV of 4

Least Severe: SV of 2.

Kavitha et al [6] discussed the severity value (S j ) for test case T j which can be expressed as equation (3), here t denote the number of faults detected by the test case T j.

t

Sj =z SV k=1

For test case T j , RDA j have been computed using severity value S j , N j is the number of defects found by T j , and time j is the time needed by T j to find those defects. The equation for RDA can be expressed as follows.

(S,xN,) rda = 12—a time

• •    Test Case Ranking

Test case Ranking is the summation of the three factors which are RFT, PFD and RDA. For test case T j , Test case ranking (TCR j ) can be calculated by the equation given below-

TCR = RFTj + PFDj + RDA          (5)

For execution, test cases are arranged in decreasing order of TCR. Test cases are ordered in such a manner, that those with greater TCR value executes earlier.

• B.    Proposed test Case Prioritization Approach

The proposed prioritization technique expressed as follows.

Input: Test suite T, and test case ranking (TCR) for every test case are inputs of the algorithm.

Output: Prioritized order of test cases.

Algorithm:

• 1.    Begin

• 2.    Set T’ empty

• 3.    For each test case T j ε T do

• 4.    Calculate test case ranking using equation (5)

• 5.    end for

• 6.    Sort T according to descending order of TCR value

• 7.    Let T’ be T

• 8.    end

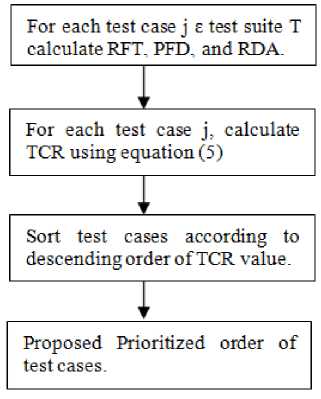
Fig. 1. Diagrammatic representation of proposed Approach

• IV.    Experiment and Analysis

For experimentation and analysis, we considered the same test suite as used in Kavitha et al. [6], they conducted an experiment to perform testing on two projects by inserting 10 faults with different severities in both projects, and finally time required by every test case to detect faults have noted by them. Table 1 represents the sample data, table 2 represents the number of faults detected by every test case, the time required to detect faults, and severity value of faults for every test case [6].

Table 1. Test case along with faults, here ‘*’ represents a corresponding fault is detected by the test case

Test Cases/ Faults	T1	T2	T3	T4	T5	T6	T7	T8	T9	T10
F1								*	*
F2		*	*		*
F3				*		*				*
F4		*	*
F5								*
F6								*	*
F7				*	*		*
F8	*					*
F9				*		*				*
F10	*							*

Table 2. Number of faults detected by every test case, the time required to detect faults, and severity value of faults for every test case

Test cases	No. of faults detected	Time	Severity
T1	2	9	6
T2	2	8	6
T3	2	14	6
T4	3	9	10
T5	2	12	8
T6	3	14	10
T7	1	11	4
T8	4	10	20
T9	2	10	12
T10	2	13	6

The values of rate of fault detection (RFT), percentage of fault detected (PFD) and risk detection ability (RDA) for test cases T1..T10 is calculated by using equation (1), equation (2) and equation (4) respectively. Table 3 represents the values for all three factors which are RFT, PFD, RDA for test case T1..T10 respectively.

Table 3. RFT, PFD, RDA for test cases T1..T10

Test cases	RFT	PFD	RDA
T1	2.22	2	1.33
T2	2.5	2	1.5
T3	1.428	2	0.857
T4	3.33	3	3.333
T5	1.66	2	1.333
T6	2.142	3	2.142
T7	0.9	1	0.3636
T8	4.0	4	8
T9	2.0	2	2.4
T10	1.538	2	0.923

For test cases, T1..T10, TCR value computed from equation (5) as given below. Table 4 shows test case ranking for each test case.

Table 4. Test case ranking for T1..T10 respectively

Test cases	Test case ranking TCR=RFT+PFD+RDA
T1	5.55
T2	6
T3	4.285
T4	9.66
T5	4.993
T6	7.284
T7	2.263
T8	16
T9	6.4
T10	4.461

For execution, test cases are arranged in decreasing order of TCR. Test cases are ordered in such a manner, that those with greater TCR value executes earlier. Hence, the prioritized order for test cases is: T8,T4,T6,T9,T2,T1,T5,T10,T3,T7.

The proposed approach is compared with different prioritization techniques such as no prioritization, reverse prioritization, random prioritization, and also with previous work of kavitha et al [6]. These approaches are compared by computing APFD (average percentage of fault detected) for each technique.

• A.    Comparison with previous work of kavitha et al.[6]

In this section, the proposed prioritized order is compared with previous work of kavitha et al [6]. Table 5 represents proposed order of test cases and the prioritized order proposed by kavitha et al [6] for the same set of test cases. APFD percentage for Kavitha et al. [6] is represented in Fig. 4.

Table 5. Test cases ordering for proposed approach and previous work [6].

Proposed order	Prioritized order in [6]
T8	T8
T4	T4
T6	T9
T9	T6
T2	T5
T1	T2
T5	T1
T10	T10
T3	T3
T7	T7

• B.    Comparison with other Prioritization Techniques

In this section, the proposed approach is compared with other prioritization techniques such as random prioritization, no prioritization, reverse prioritization. In random prioritization techniques, test cases are arranged in a random manner, in non-prioritized order test cases are arranged in the same way they are generated, in reverse prioritization, test cases are arranged in reverse way of, they are generated. Table 6 represents ordering of test cases for different prioritization techniques.

V. comparison

To quantify the aim to increase the rate of fault detection of the test suite, an APFD metric is used [1, 3, 13]. The APFD is calculated by taking the weighted average of the number of faults detected during the execution of the test suite. Let the test suite T is under evaluation, with n number of test cases. Let the number of faults contained in the program P is m. TFi be the position of first test case in test suite T that expose fault i. The formula for APFD is as follows.

APFD = 1

TF 1 + TF 2 + .. + TF m W 1

m x n       I ( 2 x n

The formula for APFD indicates that prior information about faults should be available for computation of APFD.

Table 6. Test cases ordering according to no prioritization, random, reverse and proposed prioritization techniques

No order	Random order	Reverse order	Proposed order
T1	T2	T10	T8
T2	T4	T9	T4
T3	T5	T8	T6
T4	T1	T7	T9
T5	T10	T6	T2
T6	T7	T5	T1
T7	T8	T4	T5
T8	T3	T3	T10
T9	T6	T2	T3
T10	T9	T1	T7

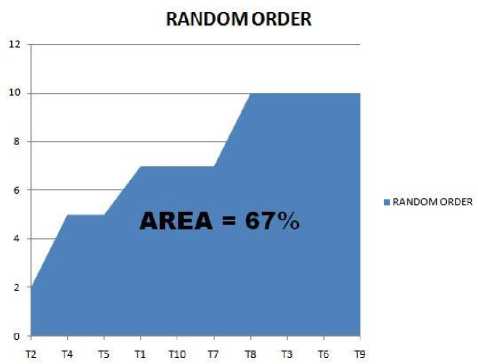
Fig. 2. APFD percentage for random prioritization

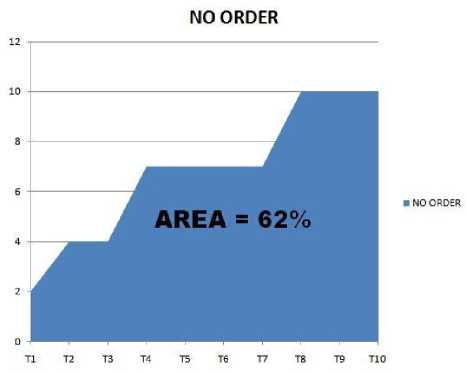
Fig. 5. APFD percentage for no order

The APFD percentage for random order, reverse order, previous work [6], no order and proposed order is represented in Fig. (2-6) respectively.

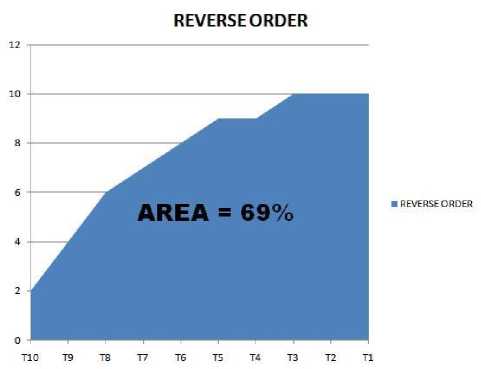
Fig. 3. APFD percentage for reverse prioritization

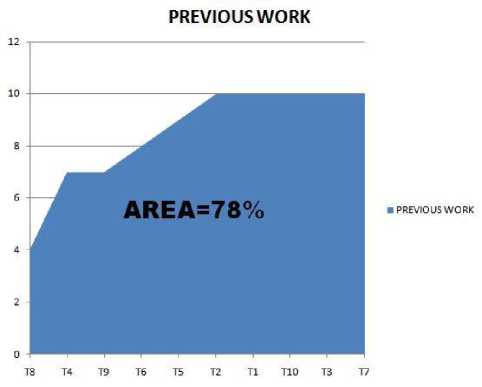
Fig. 4. APFD percentage for previous work[6]

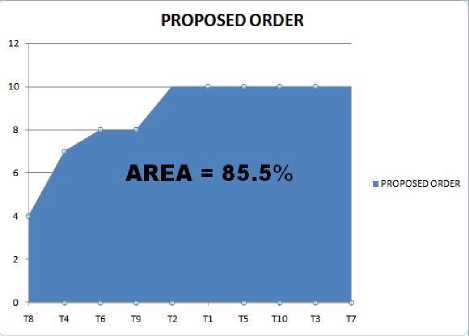
Fig. 6. APFD percentage for proposed order

• C.    Analysis

The APFD percentage for no prioritization, random prioritization, reverse prioritization, previous work [6] and proposed order represented in Table 7. The APFD percentage for proposed approach is greater than other approaches. And it can be concluded from table 7 that proposed approach outperformed other prioritization techniques, and it is a better approach.

Table 7. APFD % for no prioritization, random, reverse, previous work [6] and proposed prioritization techniques

Prioritization Technique	APFD %
No order	62
Random order	67
Reverse order	69
Previous work [6]	78
Proposed order	85.5

• VI. Conclusion

In this paper, an algorithm to prioritize test cases based on three factors which are rate of fault detection [6], percentage of fault detected and risk detection ability is proposed. Testing efficacy could be progressed by emphasizing on test cases which detect greater percentage of severe faults. For every test case all the three factors are calculated and test case ranking is computed by adding these factors for each test case. To solve the problem of test case prioritization we prioritize test cases, according to decreasing order of test case ranking value, and we obtain the prioritized order of test cases. The proposed approach is compared with different prioritization techniques such as no ordering, reverse prioritization, random prioritization, and also with previous work of kavitha et al. [6], using APFD metric. The APFD is calculated by taking the weighted average of the number of faults detected during the execution of the test suite. The results represent that proposed approach outperformed all approaches mentioned above.