An approach for the generation of higher order mutants using genetic algorithms

Published Online January 2018 in MECS

Software testing is a process that aims at making sure that a software realizes the needed requirements such as dependability and functionality as well as exhibiting high quality. A main challenge in software testing is increasing the process effectiveness within the given time and money constraints.

Mutation Testing is a white-box fault-based testing technique that works by introducing faults in a program in order to measure the adequacy of the test suite [1-2]. Empirical studies show that mutation testing is more effective in finding faults compared with other testing approaches [3-4]. The effectiveness of the test suites is measured by their ability to find the seeded faults, this is called Mutation Score (MS), or mutation adequacy [1-2], [5-6] which is computed using the equation given in (1).

=

# Killed Mutants

# Generated Mutants

∗ 100%

A test suite is run against all faulty versions of the program with the aim of detecting the seeded faults. The modified versions of the program that contain seeded faults are called mutants. If a fault is detected by any test case in the test suite; the mutant is said to be killed. When a fault is not detected by any test case in the test suite; the mutant is said to be alive, which suggest improving the test suite by adding more test cases to kill these mutants. However, a large percentage of alive mutants cannot be killed by any test case because they produce the same output as the original program. These mutants are called equivalent mutants and need to be identified and eliminated if possible. Budd and Angluin [9] proved that detecting equivalent mutants is an undecidable problem.

Many approaches were proposed to solve the problem of equivalent mutants including: compiler optimizations techniques [12], [13], approaches using mathematical constraints to automatically detect equivalent mutants [14], [15], using program slicing to assist in the detection of equivalent mutants [16], selective mutation [17], examining the impact of equivalent mutants on coverage [18], examining changes in coverage to distinguish equivalent mutants [19], and co-evolutionary search techniques [20].

Another problem of mutation testing is that in order to improve the effectiveness of a test suite, a large number of mutants needs to be generated. This requires more effort in terms of time and resources to execute these mutants which increases the execution time required to run the test suite against the generated mutants. Many approaches were proposed to solve this mutation problem including: selective mutation [17], weak mutation [21], mutant sampling approach [22], [23], using clustering algorithms to choose a subset of mutants [24], and strong nutation [25].

A promising technique to overcome the mutation testing problems is higher order mutation. Higher Order mutation testing is a mutation testing technique in which a mutant contains more than one fault. A number of studies (e.g., [26-33]) shows that higher order mutation supports solving the two problems of mutation testing, that is, help in reducing the number of generated mutants and reducing the number of equivalent mutants.

The main purpose of this paper is to present an approach for solving the problem of the large number of higher order mutants, and to reduce the number of equivalent mutants. The first problem is targeted by generating higher order mutants that are harder to kill. A hard to kill mutant is measured as a ratio of test cases that kill a higher order mutant to the whole number of test cases. A mutant that is harder to kill is also less likely to be an equivalent mutant, this is because higher order mutants include more than one fault. Therefore, the proposed approach can be used to reduce the number of equivalent mutants.

The proposed approach uses a genetic algorithm [35] for generating higher order mutants. Several studies had used genetic algorithms to generate higher order mutants, and the results they obtained are promising (e.g., [27-29]). In order to apply the proposed approach, a software tool has been implemented with Java called HOMJava (Higher Order Mutation for Java). HOMJava is an extension of a tool called muJava [36], which is a well-known tool generating first order mutants and executing tests against mutants.

The rest of the paper is organized as follows: Section 2 presents a background on higher order mutation testing, muJava, and Genetic Algorithms. Section 3 presents related work Section 4 presents the proposed approach. Section 5 presents the HOMJava tool implementation. Section 6 presents the experimental setup and the results of the experiment. Section 7 presents the conclusions and outlines future work.

• II.    Background

This section presents important terms and concepts related to the higher order mutation testing and necessary software testing terms that are used throughout this paper.

• A.    Higher Order Mutation Testing

Mutation testing is performed on a copy of the program by injecting the program with a single fault. The faulty version of the program is called mutant. Table 1 shows an example of an original program and a mutant.

Table 1. An original program and mutants

Program Version	Source Code
Original Program	int sum (int x , int y ){ return x+y ; }
Mutant	int sum (int x , int y ){ return x/y ; }
Equivalent Mutant	int sum (int x , int y ){ return x+y++ ; }

Equivalent mutant is a mutant that produces the same output as the original program, therefore, the fault that is seeded in the mutant cannot be detected by the test suite. A study by Schuler et al. [19] show that, on average, it takes about 15 minutes to manually detect a single mutant. An example of equivalent mutant is shown in Table 1.

In higher order mutation testing, instead of injecting single fault in a mutant, two or more faults are injected. The order of mutant represents the number of injected faults, that is, a mutant with two faults is a second order mutant; a mutant with three faults is a third order mutant. Table 2 shows an example of a higher order mutant with two faults, i.e. a second order mutant.

Table 2. An Example of Higher Order Mutant

Program Version	Source Code
Original Program	double average (int x , int y ){ double sum, avg ; sum=x+y; avg=sum/2 return avg ; }
Higher Order Mutant 1	double average (int x , int y ){ double sum, avg ; sum=x-y; avg=sum*2 return avg ; }

• B.    muJava

muJava [36] is a well-known Java tool for mutation testing developed by the Korean Advanced Institute of Science and Technology in South Korea and George Mason University in the United States muJava uses two techniques: Mutant Schemata Generation (MSG) [37] and bytecode translation. MSG is used for the process of generating a mutants that is called a meta-mutant, this meta-mutant is created at the source code level, and it is created so that it represents more than one mutant. While Bytecode translation is a technique for the modification and inspection of Java bytecode [36].

There are three main functions of muJava: the first function is generating mutants (first order mutants), the second function is analyzing mutants, and the third function is running test cases that the user provides against mutants. muJava uses the JDK class com.sun.tools.javac.Main for the compilation of mutants.

muJava has a Graphical User Interface (GUI) that consists of an interface for generating mutants, an interface for analyzing mutants, an interface for running test cases, and an interface for showing results of running test cases in terms of mutation score.

• C.    Genetic Algorithm

A genetic algorithm (GA) is based on theorem of natural evolution, it uses the evolution as a way to solve optimization problems in search space. Genetic algorithms were first introduced by John Holland [35].

The idea of genetic algorithms is to use techniques inspired from natural evolution including: selection, crossover and mutation to generate solutions to optimization problems. The algorithm starts with a population of candidate solutions, also called individuals.

Initial population is randomly generated.

The algorithm works through performing a number of iteration, after each iteration, the population evolves by having more fit solutions. In each iteration, a fitness function is evaluated for each individual. The optimization problem being solved has an objective function, which also has a value, the value is the fitness of each individual. As each generation rises, the fitness is increased and the more fit individuals are selected from the current population after a number of techniques such as crossover and mutation are applied. The process then repeats until a maximum number of generations has been reached or until a predefined stopping criterion is met.

Selection is applied to the population where a proportion of the current population is selected to form the new generation, the selection is based on the fitness of each individual, where the more fit individuals are more likely to be selected. After selection, the algorithm produces the next generation via the application of crossover on the selected individuals. Crossover is done by choosing two parent individuals from those selected and then they are combined to form a child (new individual), the child shares properties of the two parents depending on where the crossover occurs.

• III.    Related Work

This section presents a review of the related work on higher order mutation testing. Jia and Harman [27] proposed the concept of subsuming higher order mutants, which are mutants that are harder to kill than mutants that were used to create them. They used search based optimization techniques to achieve the task of finding subsuming HOMs for 10 C programs. Their results showed that such mutants existed for the studied programs.

Omar and Ghosh [29] proposed four approaches for generating higher order mutants for AspectJ programs, with a tool that automates these approaches and creates HOMs. AspectJ faults are classified according to where they occur, that is, faults that can occur in base classes, aspects, or in the interaction between the base classes and aspects. The four approaches proposed are based on aspect oriented programming fault models presented in

[33], [39-40].

Wedyan and Ghosh [33], and Wedyan et al. [54] used higher order mutation to generate faults for AspectJ programs. Their intend was to produce mutants of fault types that first order mutants missed. These fault types require at least two faults to exist in the program. Mateo et al. [30] presented an approach for reducing the cost of mutation testing by reducing the number of mutants through the combination of first order mutants to create second order mutants. Their study was based on the idea that testing is done at the system level instead of at the unit level (e. g. Class or method), this allows to test the interaction between interfaces, methods and classes, or the interaction with other systems.

Madeyski et al. [34] presented a systematic literature review on the equivalent mutant problem. In their review they highlighted the methods and approaches that try to solve the equivalent mutant problem, either in first order mutation or higher order mutation. They divided the solutions into three categories: Detecting equivalent mutants, suggesting equivalent mutants, and avoiding equivalent mutant generation. They proposed four second order mutation testing strategies, some of them was based on previous algorithms by Polo et al. [26].

Omar et al. [31] proposed an approach for producing subtle higher order mutants for Java and AspectJ programs using three algorithms: genetic algorithm, local search, and random search. They developed a tool for higher order mutation called HOMAJ [41] for mutating Java and AspectJ programs. The tool does the functionality of the creation, compilation and the execution of first order and higher order mutants.

Omar et al. [32] continued on their previous proposed approach [31] by introducing three new search techniques for finding subtle HOMs. The three new algoirthms are: Guided Local Search, Restricted Random Search, and Restricted Enumeration Search. To find subtle higher order mutants, they used the same objective function that they used in their previous study [31].

Derezinska et al. [42] proposed four algorithms to produce HOMs for Python programs. These algorithms are: Between-Operators, Each-Choice, FirstToLast, and Random. Their results show that the number of generated second order mutants was about half the number of first order mutants, and the third order mutants was about 33%.

Kintis et al. [43] introduced a classification technique called Isolation Equivalent Mutants (I-EQM). The technique uses second order mutants to isolate first order mutants that are likely to be equivalent. The technique uses the impact of first order mutant on another first order mutant. Nguyen and Madeyski [44] proposed an approach that is centered on the search for valuable Strongly Subsuming Higher Order Mutants, with the use of a multi objective optimization algorithm.

Tokumoto et al. [48] proposed four high-speed higher order mutation testing techniques. The four techniques are: metamutation, mutation on virtual machine, higher order split-stream execution, and online adaptation technique. They implemented these techniques in a tool called MuVM. They goals are: (1) reducing compilation cost by using bit-code mutation and metamutation in C, (2) reducing the time of testing, and (3) reducing the number of mutants. In their experiment, they compared their tool to an existing tool called MILU using two attributes, the number of generated mutants and the execution time of the mutants. The results indicate that MuVM tool is significantly superior in comparison to MILU.

Nguyen et al. [49] continued on their previous proposed approach [44] on higher order mutation testing by presenting an empirical evaluation for their approach. They applied different algorithms of multi-objective optimization, and they used their classification of HOMs, and their proposed fitness and objective functions from their previous work [44, 50-52]. Their aim was to search for HOMs that are both reasonable and of high quality, that are able to replace all of their constituent first order mutants, without risking the effectiveness of tests. Their results showed that the cost of mutation testing was reduced due to the reduction in the number of HOMs. The HOMs were also hard to kill.

In their recent study, Omar et al. [53] studied and evaluated the generation of hard to kill HOMs using six algorithms. These algorithms are: Restricted Enumeration, Local Search, Genetic Algorithm, Test-Case Guided Local Search, Data-Interaction Guided Local Search, and Restricted Random Search. They conducted an empirical study using 10 Java and AspectJ programs. Their results showed that all the proposed techniques were able to find subtle HOMs, but the Local Search and the two Guided local search algorithms were more effective than others. They also found that different algorithms can find different sets of subtle HOMs, which encourages the use of different algorithms for the production of subtle HOMs effectively.

• IV.    The Proposed Approach

The proposed approach aims to solve two problems in mutation testing, these are:

• 1.    Cost, by reducing the number of mutants

• 2.    The high percentage of equivalent mutants

The proposed approach uses a genetic algorithm for generating higher order mutants. Genetic algorithms are suitable for problems which require searching for optimal solutions in a search space. In our case, we are searching the space of higher order mutants for the fittest (hard to kill) mutants.

Genetic algorithm uses a population that consists of individuals which represent possible solutions. A solution contains chromosomes that represent the properties of that individual. In our case, the individual represents a Java source code file and a chromosome represent a line of code. Since each individual represents a higher order mutant, they contain two faults, where each fault is contained in a specific line of code.

The algorithm begins with a population of candidate solutions. Each solution in the search space is a higher order mutant. These mutants have various properties in terms of fitness and hardness to be killed. In order to begin the algorithm, at first the fitness for each of these mutants has to be calculated.

After that, selection is applied on the most-fit mutants, and crossover is performed. Then, fitness is calculated again for the newly produced mutants by crossover, and the whole process is done again. The population then evolves towards better solutions. The algorithm terminates when a predefined number of generations is reached.

The following is a detailed procedure of how the proposed genetic algorithm works:

The higher order mutants are generated using a tool called HOMAJ [41]. These generated mutants are the input to the genetic algorithm.

The genetic algorithm process is applied on the provided higher order mutants, that is, it starts with the process of selection. In order to perform selection, fitness for the whole population of mutants is calculated using (2). The fitness function ranges between 0, and 1. When the fitness of a higher order mutant is closer to 1, this means that the mutant is a very weak mutant, that is, it is killed by most of the test cases in the test suite. On the other hand, when a fitness of a higher order mutant is closer to 0, it means that this mutant is a strong mutant and it is killed by a few number of test cases from the test suite.

Fitn ess (m) =

# T e s t cas e s t h a t к i 11 e d m

#

After calculating the fitness for every mutant, selection is applied. Selection is done by eliminating the 10% least fit mutants from the population, these eliminated mutants has to be replaced by newly produced ones. This is done by choosing a subset of the remaining mutants in the population to form the parents in the crossover step. For example, if the population consists of 100 mutant, then the 10 least fit mutants will be eliminated from the population, and will be replaced by another 10 newly produced mutants, these new mutants are produced by selecting a subset of the remaining mutants as parents, so 10 parents are chosen to produce 10 new children to replace the eliminated mutants.

The next step is the crossover. In our approach, we used crossover by replacement. In this method the crossover is performed in such a way that chromosomes from the first parent are replaced with chromosomes from the second parent. In our case, a higher order mutant has two faults, chromosomes are the lines of code. So replacement is done to faults, the two parents that enter the crossover are of the most fit mutants, the goal is to produce two new children that share the properties of these parents.

After crossover by replacement, the next step is to calculate fitness for the second generation, that is, the population after eliminating the least fit mutants and producing the new mutants. Test cases are again run against mutants from the second generation and fitness is calculated based on the fitness formula given in (2).

The algorithm continues to iterate with the same steps and repeats the process until the number of predefined generations has been reached. Fig. 1 shows the process of the proposed approach.

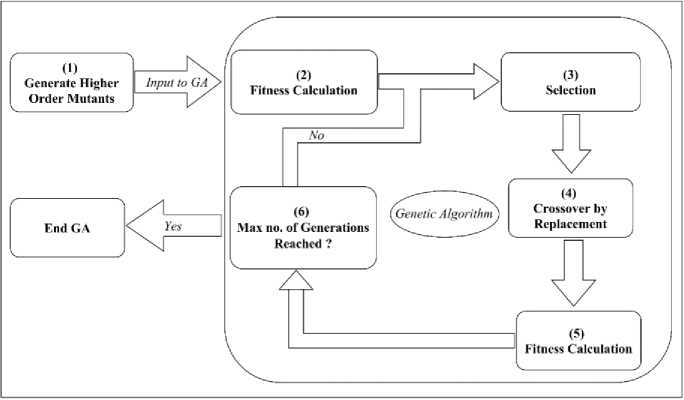
Fig.1. The process of the proposed approach

The following figures show an example of crossover by replacement. Fig. 2 represents the original code without faults, Fig. 3 and Fig. 4 show the higher order mutants with two faults represented as parents, Fig. 5 shows the new child that is produced after the crossover by replacement.

• 1    public double average ( int x, int y, int z){

• 2   double avg=0.0;

• 3   int sum=0;

• 4  sum=x+y+z;

• 5  avg=sum/3;

• 6    return avg;

• 7   }

Fig.2. Original source code of average method.

Fig. 3 shows the first HOM, which is the first parent. Note that the fifth line has the first fault, instead of adding x,y and z, it became subtracting x,y and adding z. The second fault is located in the sixth line, which changes from a division to a multiplication for the variable sum.

• 1    public double average ( int x, int y, int z){

• 2    double avg=0.0;

• 3    int sum=0;

• 4  sum=x-y+z;

• 5  avg=sum*3;

• 6    return avg;

• 7    }

Fig.3. Parent-1 source code of average method.

• 1    public double average ( int x, int y, int z){

• 2   double avg=0.0;

• 3   int sum=0;

• 4  sum=x+y*z;

• 5  avg=sum-3;

• 6    return avg;

• 7   }

Fig.4. Parent-2 source code of average method.

Fig. 4 shows the second HOM, which is the second parent. Note that the fourth line also has the first fault, instead of adding x,y and z, it became adding x,y and then multiplying by z. The second fault is located in the sixth line, which changes from a division to a subtraction for the variable sum .

Fig. 5 shows the first child that is produced after performing the crossover between parent 1 and parent 2. The first child has two faults, the first fault is from parent 2 and the second fault is from parent 1. Specifically, the fourth line has the first fault, which is the multiplication from parent 2, and the sixth line has the second fault, which is the multiplication from parent 1.

• 1    public double average ( int x, int y, int z) {

• 2    double avg=0.0;

• 3    int sum=0;

• 4    sum=x+y*z;

• 5    avg=sum*3;

• 6    return avg;

• 7   }

Fig.5. New child-1 source code of average method.

Fig. 6 shows the second child that is produced after performing the crossover between parent 1 and parent 2.

• 1    public double average ( int x, int y, int z){

• 2   double avg=0.0;

• 3   int sum=0;

• 4  sum=x-y+z;

• 5  avg=sum-3;

• 6    return avg;

• 7   }

Fig.6. New child-2 source code of average method.

The second child also has two faults, the first fault from parent 1 and the second fault from parent 2. Specifically, the fourth line has the first fault, which is the subtraction from parent 1, and the sixth line has the second fault, which is the subtraction from parent 2. Fig. 7 shows a pseudo-code of the genetic algorithm.

Fig.7. Genetic algorithm pseudo-code

• V.    HOMJava Implementation

The tool developed in this study is programmed in Java, and intended to be used with Java programs. We named our tool HOMJava. It is an extension of muJava [36], which was intended for first-order mutation testing. The tool performs the following functions: (1) creating higher order mutants, (2) running test cases against higher order mutants, (3) search for harder to kill higher order mutants using genetic algorithm.

The expected result of the tool is to apply the proposed approach and find a harder to kill higher order mutants through the use of the genetic algorithm with the application of the proposed approach. The genetic algorithm tries to find optimal solutions in the space of possible solutions, in this case higher order mutants, these mutants has to be harder to kill than the rest of the possible solutions.

• A.    Architecture of HOMJava

The architecture of the tool consists of a three layers: the GUI layer, the functional layer, and the external layer. Each layer contains a number of components each performing a well-defined task. Fig. 8 shows the architecture of HOMJava tool.

As shown in Fig. 8, each layer consists of the following components:

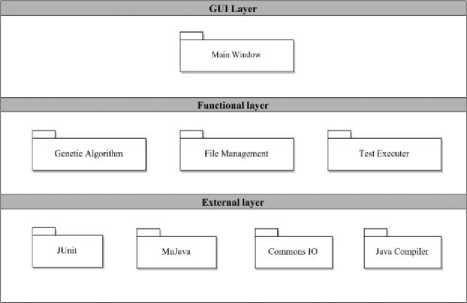
Fig.8. Architecture of HOMJava

• •    GUI Layer: this layer represents the user interface and contains one component, the Main Window . This component contains three buttons to specify original program source code file, the directory of the higher order mutants, and the directory of test suite.

• •    Functional Layer: contains the core functionalities performed by the tool. It consists of the following components: (1) Genetic Algorithm : contains the implementation of the genetic algorithm, including: crossover by replacement, selection, fitness calculation, and iterating the algorithm for the specified number of generations. (2) Test Executer : includes the module that runs the JUnit test suite against the specified higher order mutants, and reports the results. It also checks whether the class under test and the JUnit test suite and the directory of higher order mutants are correctly specified and match in terms of class name and package name. This component uses the external libraries of JUnit and muJava in order to read and run tests on mutants and report results. (3) File Management: this component encapsulates operations for file management including: (a) reading files, either source files (.java) or binary files (.class), (b) modifying files, updating of files occurs as a result of the crossover operation which is performed on the source files of the mutants, (3) writing files, occurs when files are modified and saved after each update. (new mutant is produced, or mutated). Source files are then compiled using a Java compiler. This component uses the external library called “commons IO” for handling file management.

• •    External layer : contains external libraries that are used and integrated in this tool. These libraries are: (1) JUnit : the unit testing framework for writing and running unit tests on programs in Java. This library requires another library called “hamcrest” to be also specified and integrated with the tool, (2) muJava: is used in our tool does for executing tests on mutants and assuring that mutants and original class and the test suite are correctly specified in terms of class name and package name and directories of files, (3) Commons IO: this external library is used to support the file management component, and (4) Java Compiler : used to compile the newly produced source code of the child mutants after the crossover operation.

• B.    Process of HOMJava

Fig. 9 shows the process of the tool. The process goes through the following steps:

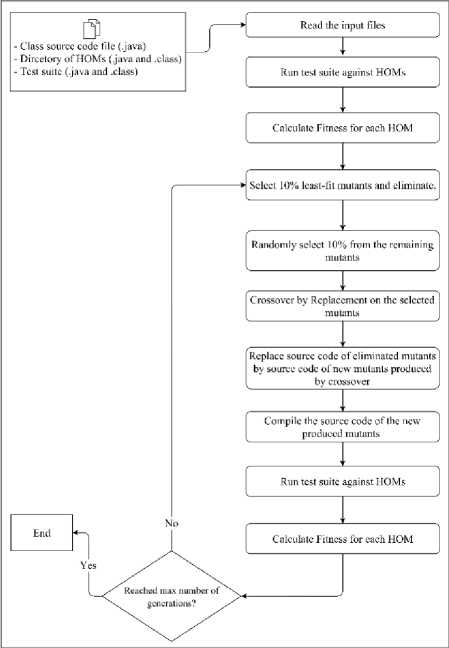
Fig.9. Flowchart representing the process of HOMJava.

• 1.    The input to the tool is the file of the original class to be tested, either in (.java or .class) extension. The directory of higher order mutants, in which each mutant is contained in a separate folder inside that directory, and the test suite file, which contains all the test cases. The main window of the tool is shown in Fig. 10.

• 2.    After all the required inputs are specified, the tool starts first through the input handler component, which processes the three inputs to the tool. First, it reads the original class to be tested. Then, it reads the directory of the mutants, and finally, it reads the test suite file.

• 3.    Test suite is run against all mutants through the test runner component. This step is necessary in order to find the fitness of the starting population. The test runner uses a component from Junit to run the test cases.

• 4.    The genetic algorithm is then started. The GA uses a component for computing the fitness value for each individual. This component, in turn, uses the result of running the test suite to calculate the fitness. The GA goes through the iterations of crossover and replacement. The GA uses a component for performing each step (crossover component, replacement component). The new produced mutants are compiled to a new higher order mutants that will replace the least-fit mutants and then are used to replace the discarded least-fit mutants. After each iteration, new mutants are saved in files, so in the end of the GA, the set of

• 5.    The results after the GA run are displayed in the text area as shown in Fig. 10. The output handler component is used prepare and display the results

fittest mutants are produced after the last iteration. The GA uses the HOM handler component for managing files.

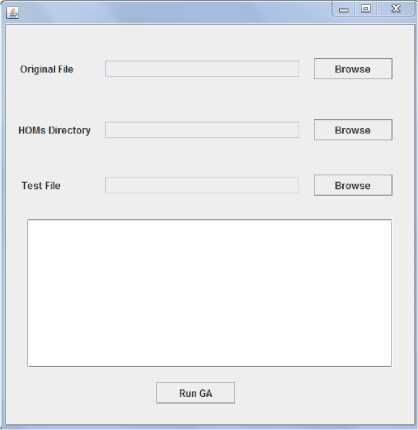
Fig.10. Main window of HOMJava

• C.    User Interface of HOMJava

The main window of HOMJava is shown in Fig. 10, this is the main and only window of the tool. The following are the contents of the window:

• 1.    The upper (first from above) “Browse” button is for choosing the source code file of the original program. It opens a file open chooser dialog for navigating the file system or entering the name of the file.

• 2.    The middle (second from above) “Browse” button is for choosing the directory that contains the higher order mutants. Each higher order mutant has its own directory that contains the source code file and the byte code file. This button also opens a file chooser dialog to navigate to or type the directory of the higher order mutants.

• 3.    The lower (third from top) “Browse” button is for choosing the test suite folder. It also opens a file chooser dialog to navigate to or type the folder containing the test suite, which has to contain the source code and byte code files of the test suite.

• 4.    The text area is where the output will be shown while running the tool.

• 5.    The “Run GA” button is for starting the genetic algorithm.

• VI.    Experiment Setup

In this section, we describe the setup of the experiment we performed to evaluate our approach. We begin by stating the research questions the experiment aims to answer, then we describe the subject program, generation of mutants, and generation of test cases.

The experiment is performed in order to answer the following research questions:

RQ1 : Can the proposed approach produce subtle higher order mutants?

RQ 2: What is the approximate percentage of equivalent mutant produced by the proposed approach?

• A.    Subject Program

We used one program to perform the experiment, the program is called OrdSet [45-46] which implements a set of ordered integers that includes a number of operations performed on this set. The program consists of 315 lines of code, contains one class which has 23 methods.

• B.    Generation of Mutants

For this step, mutants have been generated for the OrdSet class, using HOMAJ [41].

The first step was to generate first order mutants, and then using these mutants to generate higher order mutants with each mutant containing two faults. The mutants generated have mutation operators of both class level and method level (i.e. traditional mutants), with a number of operators presented in Table 3.

Table 3 shows the name of each operator, the type for each operator (method or class), a description of each operator, and number of first order mutants that were generated with each operator.

Table 3. Mutation operators used.
Operator	Type	Description	FOMs Generated
AODS	Method	Deletes arithmetic	4
	level	operator
AOIU	Method	Inserts arithmetic	10
	level	operator
COD	Method	Deletes conditional	1
	level	operator
	Method	Replaces
COR		conditional	10
	level	operator
LOI	Method	Inserts logical	10
	level	operator
ROR	Method	Replaces relational	50
	level	operator
COI	Method	Inserts conditional	10
	level	operator
AORB	Method	Replaces	40
	level	arithmetic operator
AORS	Method	Replaces	11
	level	arithmetic operator
AODU	Method	Deletes arithmetic	5
	level	operator
EAM	Class	Changes accessor	16
	level	method
IOD	Class	Overrides method	1
	level	deletion
JSD	Class	Deletes a static	3
	level	modifier
JSI	Class	Inserts a static	5
	level	modifier

• C.    Generation of Test Cases

We used a tool called Randoop [47] for generating test cases. Randoop generates test cases for Java, given the source code of the program to be tested, Randoop can generate a large number of tests according to settings the user choses in terms of number of tests and a time out for the generation process. The test suite we used consisted of 800 test case. Table 4 shows the characteristics of the subject program, the number of mutants, and number of test cases used in the experiment.

Table 4. Summary of the main attributes for the subject program.
Measure	Value
Program Name	OrdSet
#Lines of Code	315
#Classes	1
#Methods	23
#First Order Mutants	176
#Higher Order Mutants	12159
#Test Cases	800

As shown in Table 4, the number of generated higher order mutants was 12159, these higher order mutants were generated using a number of 176 first order mutants. The generation of mutants was performed using HOMAJ [41].

• D.    Genetic Algorithm setup

We configured the genetic algorithm to run for 50 generations. We run the experiments on a PC with a core-i7 processor and a 6GB of memory.

The number of mutants that entered the genetic algorithm is 2000, which were chosen from the total generated HOMs in terms of the best-fit mutants, those that are killed by the least number of test cases.

Table 5. Genetic Algorithm configuration.

Measure	Value
Program Name	OrdSet
#Generations	50
#Higher Order Mutants	2000
#Test Cases	800
Total Run Time	Approximately 530 minutes

For 50 generations, the 2000 mutants we run against a test suite of 800 test cases and then these mutants are evaluated based on the number of tests that kill each mutant from the total number of tests. In each generation, the 10% least-fit. In other words 200 mutants were replaced by newly produced 200 mutants. The new 200 mutants are produced by selecting 200 mutants of those that are most fit, and these are used to produce new mutants in the crossover by replacement process, where the 200 parent mutants will produce new 200 child mutants to replace the 200 weakest and least fit mutants.

• VII.    Results

This section reports the results of the experiment that we performed in order to answer the research questions.

• A.    Can the proposed approach produce subtle higher order mutants?

In Table 6, we show the fitness reported of the initial population of mutants used by the genetic algorithm. The fitness is calculated using a test suite consisting of 800 test cases on a set of 12159 mutants.

Table 6. Numbers of mutants, test cases, and fitness.
Measure	Value
#Higher Order Mutants	12159
#Test Cases	800
Average Fitness	0.0714243
Best Fitness	0.0
Best Fitness but killed by at least 1 test	0.00125
Worst Fitness	0.98375

The best fitness was 0, and that’s expected since there are mutants that are not killed by any test case, which can be either hard to kill or a possible equivalent mutant. For that reason, the best fitness of a mutant that was killed by at least 1 test case was considered, so that we can evaluate the fitness of a mutant that is surely not equivalent. The last number in the Table is the worst fitness, which represents the mutant that was killed by most number of test cases.

Then, the 2000 most-fit mutants were picked to enter the genetic algorithm. We calculated the fitness of the population of 2000 higher order mutants and the mutation score before starting the genetic algorithm, and after the genetic algorithm terminates. The results are shown in Table 7.

Table 7. Fitness and mutation score before and after genetic algorithm
Measure	Before Genetic Algorithm	After Genetic Algorithm
#Mutants	2000	2000
#Test Cases	800	800
Fitness	0.00109625	0.000004375
Mutation Score	50%	0.2%

As shown in Table 7, the mutants became stronger after running the genetic algorithm, and the fitness improved by about 99%. Which means that the genetic algorithm did produce subtle mutants, and those mutants were more fit that the ones used at the start of the algorithm.

It is important to mention that these results are based on a test suite of 800 test cases, results will most likely differ from these when another test suite is used since different test suite can vary in their effectiveness. If we used another test suite that is stronger, mutation score will be higher, fitness will most likely become lower too. But that does not affect that the higher order mutants are subtle because what affects the mutants before entering the genetic algorithm will also affect the result after the genetic algorithm.

In other words, the mutants that had a fitness of 0.5 when using test suite T1, might have a fitness of 0.4 when using test suite T2, which means that this mutant might not have the same chance of being selected to enter the genetic algorithm, or during the genetic algorithm, it may not proceed to the next generation. So, the test suite that is used before the genetic algorithm has to be used also during the genetic algorithm to achieve reliable results.

The mutation score result shows that the the genetic algorithm was able to produce subtle mutants. The test suite before the genetic algorithm killed half of the mutants, which after the genetic algorithm it killed less than 1% of the mutants.

• B.    What is the approximate percentage of equivalent mutants produced after executing the approach?

After running the genetic algorithm, a number of mutants were not killed by any test case, and had a fitness of 0. Which means that these can be equivalent mutants. In order to estimate the percentage of equivalent mutants, we run a larger test suite of about 500 test on a sample of 100 mutants with fitness 0. The goal of increasing the size of the test suite is to check whether adding more test cases can kill some of the mutants with fitness 0. Adding 500 test cases did kill 78 mutants, and only 22 mutants remained with a fitness of 0. Table 8 shows the results of the performed analysis.

Table 8. Results of testing a sample of 100 mutants with 0 fitness.
Measures for sample of 100 mutant	Equivalency possibility
500 Test case	22%
1500 Test case	17%
Manually written tests	4%

As shown in Table 8, a larger test suite of 1500 test was then used on the same sample of 100 mutants, after running the test cases on the mutants, only 17 mutants still had a fitness of 0. These remaining 17 mutants were manually analyzed, and manually written test cases were created to kill them, which resulted in 4 of these 17 that remained equivalent, which means, in our experiment, from the total sample of 100 mutants, only 4% were equivalent.

• VIII.    Conclusions and Future Work

We presented an approach for producing hard to kill and less possibly equivalent higher order mutants. The approach is based on using a genetic algorithm to produce higher order mutants from the fittest mutants in an initial population of higher order mutants that represent the search space.

Our contribution is a crossover by replacement in the genetic algorithm, in which faults from two parent mutants are replaced to produce two new mutants that have some properties of their parents, and in this case, the parents that are harder to kill are the ones chosen for the crossover by replacement.

The algorithm keeps running for a predefined number of generations, where every generation produces new mutants that will replace the weakest, least fit mutants.

We also developed a Java tool that applies the proposed approach, the tool is called HOMJava. To assess the effectiveness of the proposed approach, we performed an experiment using a subject program called OrdSet, which handles a set of ordered integers. Mutants were generated using HOMAJ. Test suite was generated using Randoop. The genetic algorithm was set to run for 50 generations.

The results showed that the mutants produced after running the genetic algorithm were subtle and harder to kill than those that were used at the beginning of the algorithm. The fitness was improved by about 99% compared to what it was before running the algorithm.

In terms of equivalent mutants, a sample of 100 possible equivalent mutants was taken and further tests were run on them. Of the taken sample, about 4% remained possibly equivalent mutants, and the rest were killed by at least one test case, some mutants’ required manually written tests in order to be killed.

For future work, larger experiments can be performed on the proposed approach to further assess and evaluate its effectiveness using larger programs. Our future work plans include also extending the tool for other object-oriented programming languages (e.g., C#, and C++).

Acknowledgment

The authors wish to thank Jeff Offutt for providing the source code of muJava, and El Mahdi Omar for providing us the HOMAJ tool. This work was supported in part by grant #2015/3 from Hashemite University to Fadi Wedyan.