An automated parameter tuning method for ant colony optimization for scheduling jobs in grid environment

Published Online March 2019 in MECS

The grid infrastructure [1] has evolved as the integration and collaboration of multiple computer systems, networks, different databases and other network resources The grid computing [2] has emerged as a vast computing area in the last few years. Because of the increased complexity in the scheduling part of the grid, it matches the class of NP-complete problems. The algorithms stated in [3] can be applied to scheduling jobs in grid environment are of different types, and so the grid platforms. So, it is not possible to apply a single algorithm for all the grid platforms. The conventional techniques like FCFS, however, are available to solve the problem of grid scheduling, but it increases space and time complexity and also the cost of computation. In the recent time, bio-inspired algorithms have gained substantial value over deterministic algorithms to solve NP complete problems. Those problems are optimization problems that are solved by approximate methods. Though these methods do not assure an optimal solution, but return a near-optimal solution at a low computational cost and less time.

• A.    Grid Scheduling and Scheduling Algorithms

The primary objective of grid scheduling is to reduce the job execution time and increase resource utilization. In [4] the author has explained the scheduling concept and its problem in a distributed environment like grid. In [5], the author has presented a survey report on scheduling concept which deals with the problem of scheduling and classification of scheduling techniques. In a grid environment, job scheduling poses various challenges to the researchers because of the resource heterogeneity and resource failure that may happen at any time in the grid system. So it becomes important to select an appropriate scheduling algorithm for a given set of problems and grid system. The Bio-inspired algorithms belong to family of approximate algorithms. These algorithms are inspired by nature and intelligent animals like ants, bees, humans, birds that give approximate solutions which are optimally good and sufficient for the computationally hard problems.

Evolutionary algorithms in [6] and swarm based algorithms are the components of bio-inspired algorithms. In Ref. 7, the author has discussed the importance of evolutionary algorithms applied in the field of multiobjective optimization. Swarm based algorithms [8] came into light in 1995 which was proposed by James Kennedy and Russell Eberhart. Recent trend shows ant colony optimization has remarkably proven itself as a competent and useful approach in solving complex optimization problems because of its robust and abstract behavior. ACO is specifically designed to solve minimum cost problems. In grid environment, ACO is applied to minimize the computation required by different jobs at resources distributed across multiple geographical locations.

The algorithm consists of several components which has some parameter that need to be tuned during their implementation to increase their efficiency and stability.

The topic of parameter tuning of evolutionary [9] and swarm based algorithms was initially ignored by the researchers. It is in the past few years, they have realized the significance of tuning parameters of an algorithm and how it affects the performance. The performance of jobs in grid infrastructure [10] greatly depends on the selected scheduling algorithm. The choice of scheduling algorithm is influenced by the type of job and type of grid system. The performance of a scheduling algorithm is dominated by its parameter values. This paper formulates in seven sections. The first section discusses the concept of parameter tuning and parameter control. The next section briefly explains about the bioinspired algorithms and covers some of the work that has already been done in the area of parameter tuning. In the third and fourth section, the applied methodology and its parameters have been discussed. Later, some experiments have been performed to test the tuning results and different tuning results are compared with each other in the fifth section. The parameter value for which the algorithm gives the best output is considered while others are discarded. The next section gives information about the running time complexity of the stated ACO algorithm applied in grid computing. Finally, the conclusion is discussed in the seventh section.

• B.    Problem Statement

Parameter tuning is a process of applying the modifications on the given parameters so it can be applied to a broad class of problems. This is a static approach in which the parameter values are set initially and then the algorithm is allowed to run, keeping these values constant during the entire running time of the algorithm. Therefore the problem of parameter tuning, i.e. finding appropriate parameter values is posing a big challenge to the researchers as it may lead to a low quality solution even though the algorithm is an efficient one. Although a lot of work has been done on parameter tuning for ACO, but it could not guarantee that the same set of values will be suitable for the algorithm which is customized for the grid environment. In Ref. 11 the author has stated the concept of parameter setting which is further divided into parameter tuning and parameter control. In the third section, parameter tuning is applied to the parameters of ACO algorithms as represented in Ref. 12 in grid environment and then the algorithm are executed multiple times to get a good quality solution. The author in Ref. 13 has discussed different forms of ACO and also reviewed some of the parameter adaptation strategies. Later in the empirical part, the author has compared the fixed parameter setting and prescheduled parameter variation approach.

• C.    Parameter Setting

Parameter Setting consists of : Parameter tuning and Parameter Control.

The process of tuning is done before the actual start of the algorithm and the parameter values remain same throughout runtime while control [14] tends to change the initial values that were set during run time of the algorithm. It has been seen that many of the researchers in the last decade have tried to tune the parameters manually, which took a considerable amount of time that eventually degrades the performance of an algorithm. They experimented for different parameter values and selected those values that have given the best outputs. Here we have proposed an automated algorithm for parameter tuning of ACO. Compared to other methods of tuning, it can be an efficient approach and a time saver because it reduces the time for the whole process of tuning. Since ACO is highly stochastic in nature, it is extremely required to perform multiple runs on the same problem instance for better performance and hence parameter tuning has a great role on such algorithms.

• II.    Related Works

Bio-inspired algorithms [15] are those algorithms which are inspired by biological [16] and natural phenomena. Recent trend shows that these algorithms have proven themselves fruitful in solving problems like scheduling, travelling salesman problem, data mining problems and much more. The author in Ref. 17 has taken ACO to find a solution for train scheduling problem. It was found that the proposed algorithm performed much better than the Standard Train Scheduling algorithm. The data set as taken from the standard Operational manual of Indian Railways. Not only in the grid environment, the swarm algorithm is increasingly being used in the cloud computing environment too. In Ref. 18, the author has used Bellman Ford algorithm along with ACO to find an optimal route in Vehicular Adhoc Networks (VANETs) which is a difficult task because the node availability changes dynamically. ACO is used for searching the best path for packet delivery using the amount of pheromone deposited at a particular route. The route with higher pheromone count is selected and the selected route is optimized using Bellman Ford Algorithm by calculating the distance of source to all other nodes in the network. The author in Ref. 19 has proposed a nested hybrid model which combines ACO and Genetic Algorithm (GA) to minimize the waiting time of automobiles at traffic signals.

The author has altogether used ten tuning algorithms in Ref. 20 which basically uses three different approaches REVAC, SPO and meta –EA.

The author has also highlighted the fact that tuners not only improve the performance of EA but also give vital information about the effect of different parameters on evolutionary algorithms.

In Ref. 21, the author has designed a tuning algorithm called HORA (Heuristic Oriented Racing Algorithm) which uses a heuristic method combined with racing algorithm and applied it on two metaheuristics namely Simulated Annealing and genetic algorithm. It was observed that the metaheuristics performed much better when treated with HORA as compared to a simple racing algorithm.

Eiben et al. [22] has broadly discussed the concept of parameter tuning and its subsequent benefits. Niki et al. in Ref. 23 has introduced a tuning method called Chess Rating System (CRS). It was designed to tune the parameters of the Artificial Bee Colony, Gravitational Search Algorithm and Differential Evolution. Later CRS was compared to two common tuning techniques named F-Race and Revac. The time consumption was less when tuned with CRS as compared to F-Race and Revac. Mohammadsadegh et al. [24] has applied a hybrid desirability function approach on a multi-objective Particle Swarm Optimization (MOPSO) and a fast, nondominated sorting Genetic Algorithm (NSGA-III) that optimizes the performance metrics of both the algorithm to find a solution for a single problem of machine scheduling. Oscar Castillo et al. [25] have given a method to dynamically tune the parameters of ACO to avoid slow or full convergence of the algorithm. In Ref. 26, Agasiev and Karpenko used an automated parameter tuning approach which permanently tune the parameters implemented in the program system. Iwasaki et al. [27] has discussed the qualitative and quantitative aspects of PSO algorithm and presented an adaptive PSO whose feasibility is tested with some benchmark problems like Rastrigin and Griewank. Akay and Karaboga [28] has investigated the working of artificial bee colony algorithm by analyzing the parameter change effect on the functioning of the algorithm. In the past few years, there has been a development of a number of methods which can be used to tune the evolutionary algorithms. Smit et al. [29] has demonstrated that REVAC (Relevance Estimation and Value Calibration) method can be applied as a generalized method for tuning an evolutionary algorithm to a set of problems rather than a specialized method. The parameter values, thus obtained varied from problem to problem and differs from the values thus obtained by a specialist method.

Elizabeth et al. [30] has compared four tuning methods, namely F-Race, Revac, ParamILS and SPO and evaluated its performance using Genetic Algorithm. Belarmino et al. [31] has developed a procedure called CALIBRA which evaluates up to five parameter values for a given evolutionary algorithm. Ramos et al. [32] has proposed the use of a statistical tool called logical regression to tune an evolutionary algorithm called ProtoG for Travelling Salesman Problem. Coy et al. [33] has used gradient descent and statistical design of experiments to find a method to set the parameter values for an algorithm.

Nannen and Eiben [34] studied the problem of high variance of the measurements which can be solved by measurement replication but the cost incurred is high.

During parameter setting, they developed a REVAC method to reduce measurement variance. Also, they calibrated a typical evolutionary economic simulation using REVAC method. The calibration results showed that the different measurement replication levels have a variance of the same magnitude and similar distributions. Nannen and Eiben [35] has given a method to calculate the relevance of parameters which gives information to select the most appropriate parameter value from the set of possible parameter values. Smit and Eiben [36] has used the concept of entropy to determine the parameters which are of paramount importance among the parameter set. The selection of parameter is directly proportional to the amount of impact the values of that parameter have in the applied algorithm. They used an algorithm to calculate the entropy of parameters and presented a case study showing how the entropy calculation of parameter can help in selecting the appropriate parameter which thereby helps in setting the parameter values which affects the working of the algorithm. Nannen et al . [37] has taken four evolutionary algorithm components (parent selection, survivor selection, mutation and crossover). According to each of the selected components, the choice of selecting a correct operator and cost of tuning the parameters is evaluated. It was found that mutation has the highest tuning requirement and the choice for parent selection has the utmost effect. Neyoy et al . [38] has used the concept of fuzzy logic for tuning the parameters of ACO in an Optimal Fuzzy Logic Controller design. ACO is a kind of meta heuristic whose performance greatly depends on the selected parameters. So, the idea of the author was to use fuzzy logic to introduce diversity and slow down the rate of full convergence by dynamically varying the selected parameters of ACO.

• III.    Methodology: Aco

  In late 1990s, Marco Dorigo and his colleagues found a new stochastic [39] and swarm based optimization technique called Ant Colony Optimization [40] (ACO). It is a probabilistic method [41] where ants wander randomly looking for food and as soon as they find a food source, they return to their respective nest laying pheromone (chemical entity) on the ground that forms a kind of trail from the food source to the nest. ACO is an iterative method where artificial agents construct a solution (partial solution) at each iteration by taking certain decisions. The solution obtained by ants is either good or bad. For all solutions, pheromone evaporation occurs slightly, whereas for good solutions the pheromone concentration is increased by a considerable amount.

At each iteration, some solution component is summed to the partial solution and this process terminates as soon as a stopping condition is reached and finally a complete solution is obtained. Diversity control in ACO has been a concerning issue for researchers. The author in [42] has suggested to use a fast converging search algorithm instead of slowing down the rate of convergence and also studied the effect of component alpha (α) in ACO algorithm. The problems of convergence [43] in ACO is one of the factors which affect its performance throughout its lifetime. An algorithm is said to be convergent if a solution is obtained in finite time. Likewise convergence, diversity control [44] also influences the solution of ACO. Diversity is introduced either in finding global tours or in depositing pheromones.

• A.    Basic Parameters of ACO

  Before tuning the parameters of an algorithm, it is important to understand the components of that algorithm in prior. These components may have several parameters whose values have a prominent role in the working of the algorithm. Due to the complexity involved in the operation of ACO, it becomes challenging to find an appropriate approach for parameter setting. The author in Ref. 45 has studied the effect of each and every parameter of ACO on its overall performance. In ACO, artificial ants build solution at each iteration. The important components of an ACO algorithm are ants, food source and the path which they traverse while searching for food. Initially, the building of a solution starts with a partial solution and during each iteration a new solution component is added to the partial solution. The solution component is selected with the help of a probability calculation. The probability with which kth ant moves from a state x to state y is given by (Dorigo et. Al 1991, 1996) in (1).

p _x ^k _y

(τxαy)(ηxβy)

∑ z ∈ allowed y ^{( τ} x^αz ^{).( η} x^βz ⁾

Trail updation is done as soon as all the ants have finished their solution construction. The formula for trail updation is given in (2).

τxy ← (1 - ρ)τxy + ∑k Δτxky     (2)

The probability value ( p_x^k_y ) is calculated by the Equation (1). The threshold probability ( p ₀ ) is a value which is generated by the set of the actual ( p^k ) probability values. Out of the calculated probability values, a value ( p ) is selected as threshold probability. In this paper, we are tuning the value of p and Δ τ and checking it for different cases to analyze the performance of the ACO in grid environment. A lot of work has been done by the researchers to fine tune the values of α and β .

The parameters corresponding to ACO components are discussed below:

• 1.    p^k - The probability value which helps the ant to change its state.

• 2.    p - It is the threshold probability. It is selected out of a range of probability values calculated by the above formula.

• 3.    τ - It is the measure of pheromone deposition of ants when it changes its location from one position to another. The basic theory of ACO states that higher the pheromone deposition on a path, the higher is the probability of that path being selected by the other ants.

• 4.    η - It is the attractiveness of the move which indicates the desirability of the ants to follow that path.

• 5.    α and β - These are controlling parameters in ACO which regulate the value of other parameters. α controls the concentration of pheromone deposited by the ants ( τ _xy ) on the path it traverses. The value α is normally less than 1. β controls the attractiveness of the route. Length of the route is inversely proportional to the attractiveness of the route.

• 6.    ρ - It is the pheromone evaporation coefficient.

• 7.    τ - It indicates the amount of pheromone deposited, i.e. trail level for all other feasible state transitions.

• 8.    η - It indicates the attractiveness for all other feasible state transitions.

• B.    Algorithm for ACO in Grid Computing

• 1.    Procedure Ant

• 2.  Initialize grid environment

• 3.  Initialize scheduler components

• (a)    Deposited pheromone- Δ τ

xy

• (b)    Transition probability- p^k

• (c)    Threshold probability- p

• (d)    Alpha- α

• (e)    Beta- β

• (f)    Evaporation coefficient- ρ

• 4.    Add new incoming job to the job queue Q .

• 5.    Take a job from the job queue Q .

• 6.    Select a resource R randomly.

• 7.    Test the feasibility of running job on selected resource according to ACO conditions.

• 8.    Calculate the probability value using the equation (1).

• 9.    If the resource

• 10.    Job is scheduled over the resource.

• 11.    Global update (increase) the pheromone values.

• 12.    If there is more job in the job queue

• 13.    return to step(v)

• 14.    else goto next step.

• 15.    End

else, return job to waiting queue and local update (decrease) the pheromone value and return to step (v).

• IV.    Tuning of Parameters

0.00157 to 0.00163 and the value of Δ τ  is varied from 0.1467 to 0.1473.

In this paper, the tuning process is divided into three cases as shown in Table 1.

We have tested with promising range of parameter values of ACO and it was observed that the deposited pheromone ( Δ τ ) ranging from 0.1465 to 0.1473 and threshold probability ( p ₀ ) ranging from 0.00155 to 0.00161 provides a better schedule in less time for job scheduling in grid environment on the applied algorithm.

In the first case, the value of p is fixed and the value of Δτ is varied from 0.00155 to 0.00161. In the second xy case, the value of p0 is varied from 0.1467 to 0.1473 and the value of Δτ  is kept constant. In the third case, both p0 and Δτ  are tuned. The value of p0 is varied from

Table 1. Process of Tuning

Case No.	Δ τ xy	p 0
Case 1	Tuned	Fixed
Case 2	Fixed	Tuned
Case 3	Tuned	Tuned

• A. Algorithm for Tuning

The algorithm for tuning parameters of ACO is given below:

Initialize:

Number of iterations=n

Step 1: Repeat step 2 to step 4 till n number of iterations.

Step 2: Δτxy is incremented by 0.00002 for Case 1 and case 3 while fixed for Case 2.

Step 3: p is kept constant for Case 1 and incremented by 0.002 for Case 2 and Case 3.

Step 4: Run step 2 and step 3

Step 5: If jobs are available in the job queue go to step 1

Step 6: Compare the results when simulation for all iterations is done.

• V.    Experimental Setup

  Alea is an extension of the GridSim simulation toolkit. In Ref. 46 the author describes a scheduling simulator for the grid environment called Alea whose properties are derived from a popular simulating toolkit i.e. GridSim. It is an extended version of Alea developed in 2007 which included new features like improved design, higher scalability as well as simulation speed and a new visualization interface. GridSim [47] is a Java library created to virtually set up a grid environment. Alea utilizes the GridSim library to provide support for running scheduling tasks in a grid environment. Presently, there are a large number of academic institutions and industries which are utilizing grid computing to solve complex engineering and scientific problems. The author in Ref. 48 has discussed the widespread application of grid computing across various areas. Some of the universities in the world have included grid computing as a subject in their distributed computing curriculum. Also, there are different simulators which can be used to test various applications in the grid environment. MetaCentrum is the Czech National Grid Infrastructure which provided the workload log called a Zewura Workload log. There are 7 Zewura clusters. Each cluster comprises 20 shared memory machine and each machine has 80 CPUs and 512 GB of RAM. There are altogether 3000 jobs in (SWF) format, Standard Workload Format scheduled using ant colony optimization.

• A. Performance Evaluation

Calculation of number of CPUs saved.

Requested CPUs= Δ

Used CPUs = β

Number of days = n

Number of CPUs saved = Gap between requested CPUs and available CPUs = Difference between the requested CPUs and Used CPUs = γ nn

∑ γ =∑ ∫ Δ-∑ ∫ β        (3)

Calculation of number of idle CPUs, though demand is high.

Available CPUs= β

Used CPUs= α

Number of days= n

Number of idle CPUs = Difference between the available CPUs and Used CPUs= θ nn

∑ θ =∑ ∫ β -∑ ∫ α         (4)

Case 1: Deposited pheromone is tuned and threshold probability is constant.

Table 2. Tuning of Δ τ _xy with p as constant.

SL. NO.	Δ τ xy	p 0
i	0.00155	0.1465
ii	0.00157	0.1465
iii	0.00159	0.1465
iv	0.00161	0.1465

In the first case, we have tested with four different values for deposited pheromone while keeping the value of threshold probability constant for all the four iterations as shown in Table 2 and subsequent graphs were plotted as shown in Fig. 1., Fig. 2., Fig. 3. and Fig.4. In Fig. 1., the blue curve depicts the total number of requested CPUs whereas the green curve shows the number of used CPUs. The peak in the blue curve indicates that at that particular time, requests for the CPU was too high. So, the desirable situation will be one when the number of blue peaks will be less. The red line is the number of CPUs available for execution.

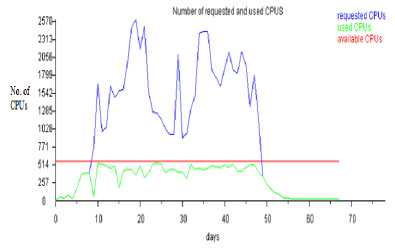
Fig.1. Number of requested and used CPUs when Δ τ _xy = 0.00155,

p ₀ = 0.1465

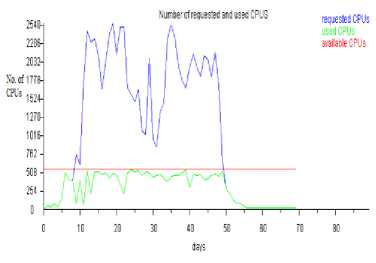
p ₀ = 0.1465

Fig.2. Number of requested and used CPUs when Δ τ _xy = 0.00157,

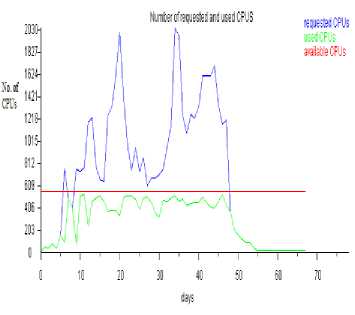
p ₀ = 0.1465

Fig.3. Number of requested and used CPUs when Δ τ _xy = 0.00159,

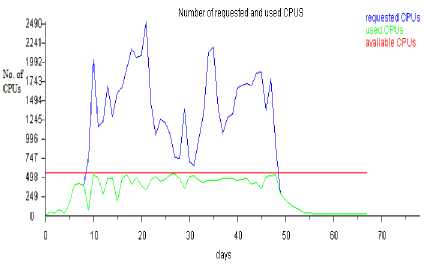
Fig.4. Number of requested and used CPUs when Δτxy = 0.00161, p0 = 0.1465

Table 3. Number of saved and idle CPUs for tuning of Δ τ _xy

Δ τ xy is tuned and p 0 is fixed, i.e. 0.1465	No. of CPUs saved γ =Δ- β	No. of idle CPUs, though demand is high θ = α - β
Δ τ xy = 0.00155	64,736	1452
Δ τ  = 0.00157 xy	60,090	3610
Δ τ  = 0.00159 xy	32,722	1775
Δ τ xy = 0.00161	35,929	1462

Out of the possible combinations, for Δ τ  = 0.00155

xy and p = 0.1465, the value of γ being highest and the value of θ is lowest as shown in Table 3. So, this is the best combination out of the other combinations.

Average number of CPUs saved= (64736+60090+32722+35929)/4 = 48369.25 = 48369

Case 2: Deposited pheromone is kept constant and threshold probability is tuned.

In the second case, we have tested with four different values for threshold probability while keeping the value of deposited pheromone constant for all the four iterations as given in Table 4 and subsequent graphs were plotted as shown in Fig. 5., Fig. 6., Fig. 7. and Fig. 8.

Table 4.Tunning of p ₀ with Δ τ _xy as constant

SL. NO.	Δ τ xy	p 0
i	0.00155	0.1467
ii	0.00155	0.1469
iii	0.00155	0.1471
iv	0.00155	0.1473

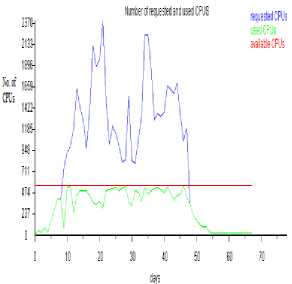
Fig.7. Number of requested and used CPUs when Δ τ _xy = 0.00155,

p ₀ = 0.1467

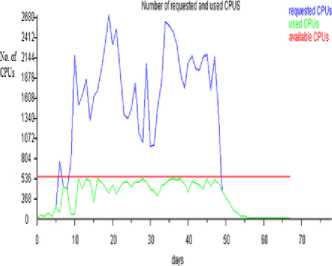
p ₀ = 0.1471

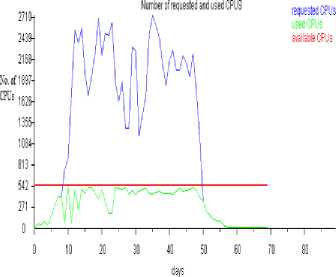
Fig.8. Number of requested and used CPUs when Δ τ _xy = 0.00155, p ₀ = 0.1473

Fig.5. Number of requested and used CPUs when Δ τ _xy = 0.00155,

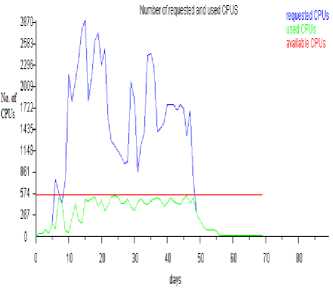
Fig.6. Number of requested and used CPUs when Δ τ _xy = 0.00155, p ₀ = 0.1469

Table 5. Number of saved and idle CPUs for tuning of p ₀

p 0 is tuned and Δ τ xy is fixed, i.e. 0.00155	No. of CPUs saved γ =Δ- β	No. of idle CPUs, though demand is high θ = α - β
p 0 = 0.1467	27,751	2891
p 0 = 0.1469	66,672	4242
p 0 = 0.1471	54,185	3950
p 0 = 0.1473	71,485	4800

In this case, the first combination = 0.00155 and xy p0 = 0.1467 has least number of idle CPUs, but the fourth combination, i.e. Δτ = 0.00155 and p0 = 0.1473 has maximum number of saved CPUs as shown in Table 5. So, the desirable combination of deposited pheromone and threshold probability can be either of the above two mentioned combinations.

Average number of CPUs saved= (27751+66672+54185+71485)/4 = 55023.25 = 55023

Case 3: Deposited pheromone as well as threshold probability is tuned.

Table 6. Tuning of both Δ τ _xy and p ₀

SL. NO	Δ τ xy	p 0
i	0.00157	0.1467
ii	0.00159	0.1469
iii	0.00161	0.1471
iv	0.00163	0.1473

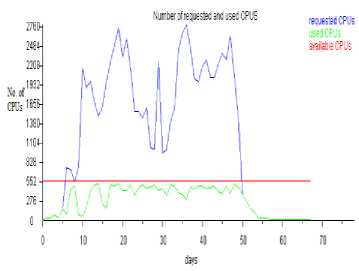
Fig.9. Number of requested and used CPUs when Δ τ _xy = 0.00157, p ₀ = 0.1467

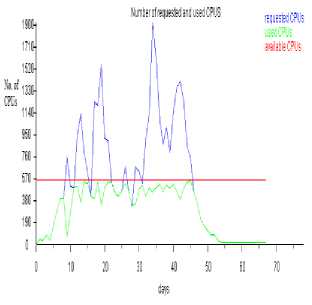
Fig.10. Number of requested and used CPUs when Δτxy= 0.00159, p0 = 0.1469

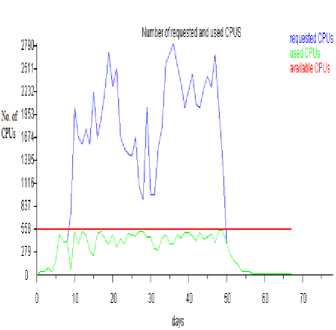
Fig.11. Number of requested and used CPUs when Δ τ _xy = 0.00161, p ₀ = 0.1471

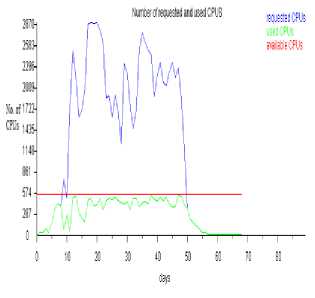
Fig.12. Number of requested and used CPUs when Δ τ _xy = 0.00163, p ₀ = 0.1473

Table 7. Number of saved and idle CPUs for tuning of both Δ τ _xy and p ₀

Both Δ τ xy and p 0 are tuned	No. of CPUs saved γ =Δ- β	No. of idle CPUs, though demand is high θ = α - β
Δ τ xy =0.00157 p 0 = 0.1467	49,090	1130
Δ τ xy =0.00159 p 0 = 0.1469	6,635	1685
Δ τ xy =0.00161 p 0 = 0.1471	66,912	1381
Δ τ xy =0.00163 p 0 = 0.1473	55,641	1869

In Table 7, the value of γ is maximum for Δ τ =0.00161 and p =0.1471. But the value of θ is minimum for Δ τ = 0.00157 and p = 0.1467. So, the desirable combination of Δ τ and p ₀ can be either of the above two mentioned cases.

From the above result, it can be concluded that the parameter tuning for ACO works best for case 1 when deposited pheromone i.e.  Δτ  is tuned and threshold probability, i.e. p is kept constant. The best combination of parameter values obtained so far are Δτ = 0.00155 and p0= 0.1465.

Average number of CPUs saved= (49090+6635+66912+55641)/4 = 44569.5 = 44569

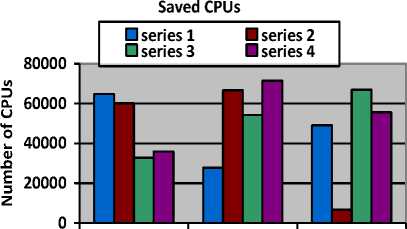
Case 1

Case 2        Case 3

Number of Cases

Fig.13. Number of CPUs saved in each case

The number of CPUs saved in each case is clearly visible in the Fig.13. For each case, four different tuning results were obtained and corresponding graphs were plotted as shown various figures above.

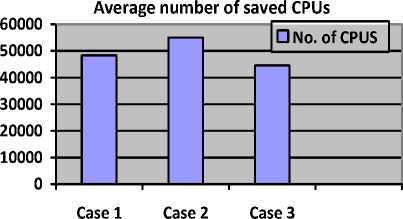
Number of cases

Fig.14. Average number of CPUs saved in each case

The Fig.14. shows that though the maximum number of CPUs were saved in the second case, but the tuning of ACO worked best for case 1 when deposited pheromone i.e. Δ τ is tuned and threshold probability, i.e. p ₀ is kept constant.

• VI.    Running Time Complexity of Aco Algorithm

ACO is a randomized algorithm. In the grid environment, the jobs are treated as ants and the pheromone value is updated (local and global) each time a job is assigned or denied a resource. So, in the simplest case, the running time will be initialized as O (m + n) where m denotes the number of jobs and n is the selection of resources (pheromone values) that have to be made for scheduling in the grid environment. In the worst case, the complexity can be O (m.n) because m jobs will make a simple selection of n resources which requires running time of O (n). There are two possible cases when the number of jobs is greater or less than the number of nodes (resources) stated below:

If m > n then

Worst case time complexity = O (n2.k) = O (n2) else

Worst case time complexity = O (n.k) =O (n), where k is some constant value.

The theoretical complexity is also justified by the different cases of running time complexity in our implementation.

• VII.    Conclusion

In this paper, a tuning method has been presented for Ant Colony Optimization in grid environment. A bioinspired algorithm like ACO with good parameter values, gives better performance as compared to the ACO with poorly chosen parameter values. With the above discussion, it can be deduced that parameter values of a scheduling technique indirectly affect the overall performance of the grid environment. Though the process of tuning is time consuming and requires immense effort to get a quality solution. So, if tuning is done under time restrictions, it may lead to a poor quality solution. It is notable that the process of parameter tuning is much easier than parameter control because the process of tuning is static in nature while the latter one is dynamic.

• [1]    I. Foster, C. Kesselmen and S. Tuecke, “The anatomy of the Grid: Enabling Scalable Virtual Organisations,” International Journal of High Performance Computing Applications, vol. 15, pp. 200-222, 2001

• [2]  I. Foster and C. Kesselmen, “The Grid: Blueprint for a

  future computing infrastructure,” ACM Digital Library , Morgan Kaufmann Publishers, 1999, pp. 1-593.

• [3]    A. Yousif, SM. Nor, AH. Abdualla and MB. Bashi, “Job Scheduling algorithms on grid computing: State-of- the art,” International Journal of Grid Distribution Computing , vol. 8, pp. 125-140, 2015.

• [4]    HB. Prajapati and VA.  Shah, “Scheduling in Grid

  Computing Environment. Fourth International Conference on Advance Computing and Communication Technologies ”, Rohtak, India, 2014.

• [5]    MK. Mishra, YS. Patel, Y. Rout and GB. Mund, “A survey on scheduling heuristics in grid computing environment”, I.J. Modern Education and Computer Science, vol. 10, pp. 57-83, 2014.

• [6]    X. Yu, “Introduction to Evolutionary Algorithms,” 40th International Conference on Computers & Indutrial Engineering , Awaji, Japan, 2010, pp. 1-1.

• [7]    K. Deb, “Multi-Objective optimization using Evolutionary algorithms An Introduction,” in Wang L., Ng A., Deb K. (eds) Multi-Objective Evolutionary Optimisation using for product design and manufacturing, Springer, London, 2011, pp. 3-34.

• [8]    SA. Ludwigand, A. Moallem, “Swarm Intelligence Approaches for Grid Load Balancing,” Journal of Grid Computing, vol. 8, pp. 279-301, 2011.

• [9]    V. Nannen and AE. Eiben, “A method for parameter calibration and relevance estimation in evolutionary algorithms,” Proceedings of the Genetic and Evolutionary Computation Conference , GECCO’06, Morgan Kauffman, San Francisco, 2006, pp. 183-190.

• [10]    M. Baker, R. Buyya and D. Laforenza, “Grids and Grid technologies for wide area distributed computing,” International Journal of Software:  Practice and

  Experience (SPE) , vol. 32, pp. 1437-1466, 2002.

• [11]    AE. Eiben, SK. Smit, “Evolutionary Algorithms and Methods to tune them,” in Hamadi Y., Monfroy E., Saubion F. (Eds) Autonomous Search, Springer, Berlin, Heidelberg, 2011, pp. 15-36.

• [12]    KY. Wong, K. Komarudin, “Parameter tuning for ant colony optimization: A review”. International Conference on Computer and Communication Engineering, Kuala Lumpur, Malaysia, 2008, pp. 542-545.

• [13]    T. Stutzle et al., “Parameter Adaptation in Ant Colony Optimization,” in Hamadi Y., Monfroy E., Saubion F . (eds) Autonomous Search, Springer, Berlin, Heidelberg, 2011, pp. 191-215.

• [14]    AE. Eiben, R. Hinterding and Z. Michalewicz, “Parameter control in evolutionary algorithms,” IEEE Transactions on Evolutionary Computation , vol. 3, pp. 124-141, 1999.

• [15]    O. Castillo, R. Martinez-Marroquin, P. Melin, F. Valdez and J. Soria, “Comparitive study of Bio-inspired algorithms applied to the optimization of type-1 and type-2 fuzzy controllers for an autonomous mobile root,” Information Science , vol. 192, pp. 19-38, 2012.

• [16]    R. Ugolotti, S. Cagnoni, “Analysis of Evolutionary

  algorithms using multi-objective parameter tuning,” Proceedings of the 2014 Annual Conference on Genetic and Evolutionary Computation, Vancouver, Canada, 2014, pp. 1343-1350.

• [17]    SK. Sahana and PK. Mahanti, “Ant Colony Optimization for Train Scheduling” I.J. Intelligent Systems and Applications, vol. 2, pp. 29-36, 2014.

• [18]    Yogesh and P. Singh, “Favorable Trail detection using ACO-BellMan Algorithm in VANETs”, I.J. Modern Education and Computer Science, vol. 1, pp. 33-39, 2016.

• [19]    S.Srivastava, SK. Sahana, Nested Hybrid Evolutionary Model for traffic signal   optimization”,   Applied

  Intelligence , Springer, vol. 46, pp. 1-11, 2016.

• [20]    AE. Eiben, SK. Smit, “Comparing parameter tuning methods for Evolutionary Algorithms,” Proceedings IEEE Congress on Evolutionary Computation , Trondheim, Norway, 2009, pp. 399-406.

• [21]    EBM. Barbosa, ELF. Senne, “Improving the fine tuning of metaheuristics: An Approach Combining design of Experiments and Racing algorithms,” Journal of Optimization, pp. 1-7, 2017.

• [22]    AE. Eiben, SK. Smit., “Parameter tuning for configuring and analyzing evolutionary algorithms,” Swarm and Evolutionary Computations, vol. 1, pp.19-31, 2011.

• [23]    N. Vecek, M. Mernik, B. Filipic and M. Crepinsek, “Parameter tuning with Chess Rating System (CRS-Tuning) for meta heuristic algorithms,” Information Sciences, vol. 372, pp. 446-469, 2016.

• [24]    M. Mobin, SM. Mousavi, M. Komaki and M. Tavana, “A hybrid desirability function approach for tuning parameters in evolutionary optimization algorithms,” Measurement , vol. 114, pp. 417- 427, 2018.

• [25]    O. Castillo, H. Neyoy, J. Soria, P. Melin and F. Vldez “A new approach for dynamic fuzzy logic parameter tuning in Ant Colony Optimization and its application in fuzzy control of a mobile robot,” Applied Soft Computing, vol. 28, pp. 150-159, 2015.

• [26]    T. Agasiev and A. Karpenko, “The program system for automated parameter tuning of optimization algorithms,” Procedia Computer Science , vol. 103, pp. 347-354, 2016.

• [27]    N. Iwasaki, K. Yasuda and G. Ueno, “Dynamic parameter tuning of particle Swarm Optimization,” IEEEJ Trans.

Electr. Electron. Eng , vol. 1, pp. 353-363, 2006.

• [28]    B. Akay and D. Karaboga, Parameter tuning for the artificial bee colony algorithm. International conference on Computational Collective Intelligence , Berlin, Heidelberg, 2009, pp. 608-619.

• [29]    SK. Smit and AE. Eiben, “Parameter Tuning of Evolutionary Algorithms: Generalist vs Specialist. in Di Chio C. et al. (eds), Applications of Evolutionary Computation. EvoApplications, Lecture Notes in Computer Science, Berlin, Heidelberg, 2010, pp. 542-551.

• [30]    E. Montero, M-C Riff and B. Neveu, “A beginner’s guide to tuning methods,” Applied Soft Computing , vol. 17, pp.39-51, 2014.

• [31]    B. Adenso-Diaz and M. Laguna, “Fine-tuning of algorithms using fractional experimental designs and local search,” Operational Research , vol. 54, pp. 99-114, 2006.

• [32]    ICO. Ramos, R. Goldbarg, E. Goldbarg and A. Neto, “Logistic regression for fine tuning of an evolutionary algorithm,” Proceedings of the 2005 IEEE Congress on Evolutionary Computation , Edinburgh, UK, 2005, pp. 1061-1068.

• [33]    SP. Coy, BL. Golden, GC. Runger and EA.Wasil, Using experimental design to find effective parameter settings for heuristics. Journal of Heuristics , vol. 5, pp. 77-97, 2001.

• [34]    V. Nannen and AE. Eiben, “Efficient relevance estimation and value calibration of evolutionary algorithm parameters,” IEEE Congress on Evolutionary Computation , Singapore, 2007, pp. 103-110.

• [35]    V. Nannen and AE. Eiben, “A method for parameter calibration and relevance estimation in evolutionary algorithms,” Proceedings of the Genetic and Evolutionary Computation Conference, GECCO’06 , San Francisco, 2006. pp. 183-190.

• [36]    SK. Smit and AE. Eiben, “Using Entropy for parameter analysis of Evolutionary algorithms,” in Bartz-Beielstein T., Chiarandini M, Paquete L., Preuss  M( Eds.),

  Experimental Methods for the Analysis of Optimization Algorithms, Berlin, Heidelberg, 2010, pp. 287–310.

• [37]    V. Nannen , SK. Smit and AE. Eiben, “Costs and Benefits of tuning parameters of evolutionary algorithms,” in Rudolph G., Jansen T., Lucas SM., Poloni C., Beume N . (Eds.), Parallel Problem Solving from Nature – PPSN X, Lecture Notes in Computer Science, Berlin, Heidelberg, 2008, pp. 528–538.

• [38]    H. Neyoy, O. Castillo and J. Soria, “Fuzzy Logic for Dynamic Parameter Tuning in ACO and its applications in optimal fuzzy logic controller design,” in Castillo O., Melin P .(eds) Fuzzy Logic Augmentation of Nature-Inspired Optimization Metaheuristics. Studies in Computational Intelligence, (2014), Springer, Cham, pp. 3-28.

• [39]    M. Dorigo, C. Blum, “Ant Colony Optimization theory: A Survey,” Theoretical Computer Science , Elsevier, vol. 344, pp. 243-278, 2005.

• [40]    C. Blum, “Ant Colony Optimization: Introduction and recent trends,” Physics of Life Reviews , vol. 2, pp. 353373, 2005.

• [41]    D. Merkle, M. Mddendorf and H. Schmeck, “Ant Colony optimization for resource constrained project scheduling,” IEEE Trans. Evolutionary Computation , vol.6, pp. 333346, 2002.

• [42]    B. Meyer, “Convergence control in ACO,” Genetic and Evolutionary computation conference (GECCO) , Seattle, WA, 2004.

• [43]    D. Merkle and M. Middendorf, “Prospects for dynamic algorithm control: lessons from the phase structure of ant

  scheduling algorithms,” in R.B. Heckendorn (ed.), Proceedings of the 2000 Genetic and Evolutionary Computation Conference- Workshop Program. Workshop- The next ten years of scheduling research, Morgan Kaufmann Publishers, Las Vegas, USA, 2001, pp. 121-126.

• [44]    Y. Nakamichi and T. Arita, “Diversity control in Ant Colony Optimization,” Proc. Inaugural Workshop on Artificial Life (AL’01), Adelaide, Australia, 2001, pp. 7078.

• [45]    A. Sieminski, “Ant Colony Optimization Parameter evaluation,” in Zgrzywa A., Choros K., Sieminski A . (eds) Multimedia and Internet Systems: Theory and Practice. Advances in Intelligent Systems and Computing, (Springer, Berlin, Hidelberg, 2013), pp. 143-153.

• [46]    D. Klusacek and H. Rudova, “Alea 2- Job Scheduling Simulator,”   Proceedings of the  3^rd  international

conference  on simulation  tools and techniques

(SIMUTools 2010), (ICST 2010).

• [47]    R. Buyya and M. Murshed M, “GridSim: A toolkit for the modeling and simulation of Distributed Resource Management and Scheduling for grid computing” the journal of concurrency and computation: Practice and Experience (CCPE) , vol. 14, pp. 1035-1593, 2002.

• [48]    M. Murshed and R. Buyya, “Using the GridSim toolkit for Enabling Grid Computing Education,” Proceedings of the International Conference on Communication Networks and Distributed Systems Modeling and Simulation , San Antonio, Texas, USA, 2002.

Optimization for Scheduling International Journal of

Applications(IJISA), Vol.11, 10.5815/ijisa.2019.03.02