An Efficient Diffusion Load Balancing Algorithm in Distributed System

Published Online July 2014 in MECS

A distributed computing system (DCS) is a set of processors (nodes) connected through a network. Distributed network is mainly heterogeneous in nature in the sense that the processing nodes, network topology, communication medium, operating system etc. may be different in different network which are widely distributed over the globe [1-4]. Presently several hundred computers are connected to build the distributed computing system [3, 5-7]. In order to get the maximum efficiency of a system the overall work load has to be distributed among the nodes according to their performance over the network. So the issue of load balancing became popular due to the existence of distributed memory multiprocessor computing systems [8].

The main purpose of the DCS is to share the resources in a best way available in the network. So one of the best way to utilize and to share the network resources is through the load balancing among the processors. In DCS generally some processors may have more numbers of jobs and some others may have less numbers of jobs or even idle causing inequality of job distribution on different processors resulting low performance of the system. And the performance of a system is considered to be the performance of the slowest node in the network.

Some time it is observed in the network that at peak time the fastest processors are idle or lightly loaded and the slower nodes are heavily loaded. So load balancing can be done by transferring excess load from the heavily loaded nodes to the lightly loaded nodes so that the load on each node becomes approximately the same. The load balancing algorithms improve the overall performance of the system by exploiting maximum power of the processors and minimizing the average response time.

The distribution of loads to the processing elements is simply called the load balancing problem. In a system with multiple nodes there is a very high chance that some nodes will be idle while the other will be over loaded. The goal of the load balancing algorithms is to maintain the load to each processing element such that all the processing elements become neither overloaded nor idle that means each processing element ideally has equal load at any moment of time during execution to obtain the maximum performance (minimum execution time) of the system [9-13]. So the proper design of a load balancing algorithm may significantly improve the performance of the system.

In the network there will be some fast computing nodes and slow computing nodes. If we do not account the processing speed and communication speed (bandwidth), the performance of the overall system will be restricted by the slowest running node in the network [13]. Thus load balancing strategies balance the loads across the nodes by preventing the nodes to be idle and the other nodes to be overwhelmed. Furthermore, load balancing strategies removes the idleness of any node at run time.

The need of load balancing arises from the concept that there is a very little probability that the load to a system will be distributed according to the processing power of the nodes. In the network some nodes will be highly loaded and some will be lightly loaded or idle sometimes as a result the performance of the system will be considerably degraded which can be resolved in an optimized way through the load balancing strategies which deals with assigning the tasks to each processor according to the speed and bandwidth of the communication link to obtain the maximum performance (minimum execution time) of the system [ 8,14-16] .

During the design of a dynamic load balancing algorithm the following issues are considered [11,15]: Assignment which assigns the jobs to the processors according to the situation in a system; load Calculation which tells how to calculate the workload of a particular node in a system; job transfer which determines whether a job is to be executed locally or remotely, this also defines when a node becomes overloaded; system State which tells whether a node is overloaded or lightly loaded; priority assignment which tells the priority of execution of local and remote processes at a particular node and information exchange which tells how to exchange the system load information among the nodes. The information policy includes the following steps [17]: processors begin to collect load information of other nodes when load balancing operation is going to start which is called on demand information policy; processors inform their load information at regular interval to the other nodes which either may not be interested which is known as periodical information policy and when a processor changed its state, it immediately informs the others by passing information which is called On-state change information policy. Migration limiting which determines frequency of transfer that how many of times a process can migrate from one node to another.

There are two fundamental approaches to the load balancing algorithm design. In static load balancing design approach the tasks are assigned on the basis of priori knowledge of the system and once the tasks are allocated on the nodes do not change [5,20]. The load balancing    decisions are determined either deterministically or probabilistically at compile time and remain unchanged during run time. The performance of the static load balancing algorithms depends on the prior information about the tasks and the system. The decision to transfer the tasks does not depend on the system state change. This approach is widely applicable because of its simplicity and the minimized run-time overhead. During the static load balancing too much information about the system and jobs must be known before the execution. This information may not be available in advance and the thorough study on the system state and the jobs is quite tedious approach in advance. However static approaches do not respond to a dynamic run-time environment and may lead to load imbalance on some nodes and significantly increase the job response time. Most of the loosely coupled distributed systems exhibit significant dynamic behavior, having load varied with time. So, dynamic load balancing algorithm came into existence. The assignment of jobs is done at the runtime. So the dynamic load balancing algorithms take the decision to transfer the tasks depending on the current state of the system. The tasks are transferred from heavily loaded node to the lightly loaded node [15,20]. So the quality of dynamic load balancing algorithms depends on the collection of information of load on different nodes in the system. The information may be collected either by centralized or distributed approach. In centralized approach the information is collected by a specially designed central node and in distributed approach each node has the autonomy to collect the information about the load of the system. In distributed information collection policy the information is collected either by sender initiative or receiver initiative algorithm. In sender initiative approach the heavily loaded nodes search for lightly loaded nodes for transferring extra load and the receiver initiative approach is the converse of sender initiated approach. Dynamic load balancing policies are considered to be better to respond to changing environments and to avoid states that result in poor performance. The drawbacks of the dynamic load balancing policies are that these policies are more complex than their static load balancing policies because dynamic load balancing policies require information on the run-time load and activities of state collection. Dynamic load balancing algorithms surely incur non-zero run-time overhead due to the communication costs of load information collection and distribution. A good dynamic load balancing algorithm always minimized these costs.

Hybrid algorithms [18, 19] combine the advantages of both static and dynamic policies. Static algorithm is considered a coarse adjustment and the dynamic algorithm a fine adjustment in hybrid algorithm. When the static algorithm is used, load imbalance may result. Once this happens, the dynamic algorithm starts to work and guarantees that jobs in the queues are balanced in the entire system.

The dynamic load balancing approach has three most important policies: transfer policy, information policy and location policy [21,22,24]. Transfer policy decides depending upon some predefined value whether a job would be executed locally or remotely. In selection policy the load balancing node select suitable node for transferring the selected job depending upon the state information collected by information policy. Both sender initiated and receiver initiated approaches fall under the location policy.

Practically load balancing decisions are taken jointly by location and distribution rules [ 15,32 ]. The balancing domains are of two types: local and global. In local domain, the balancing decision is taken from a group of nearest neighbors by exchanging the local workload information while in global domain the balancing decision is taken by triggering transfer partners across the whole system and it exchanges work load information globally.

Benefits of load balancing algorithm are: load balancing improves the performance of each node and hence the overall system performance; load balancing reduces the job idle time; small jobs do not suffer from long starvation; maximum utilization of resources; response time becomes shorter; higher throughput; higher reliability; low cost but high gain; extensibility and incremental growth.

The remainder of this paper is organized as follows. Section II discusses the related work on different diffusion algorithms. Section III presents the basic notations to represent a distributed computing system. In section IV we make the problem formulation. In section

V complexity of the proposed algorithm is evaluated. In section VI result and discussion are given and over heads in worst case and optimal cases are presented in tabular form and in pictorial form as well. And a conclusion is drawn in section VII.

• II.    Related Work

Load balancing is the way of distributing load units (jobs or tasks) across a set of processors which are connected to a network which may be distributed across the globe. The excess load or remaining unexecuted load from a processor is migrated to other processors which have load below the threshold load [ 5]. Threshold load is such an amount of load to a processor that any load may come further to that processor. In a system with multiple nodes there is a very high chance that some nodes will be idle while the other will be over loaded. So the processors in a system can be identified according to their present load as heavily loaded processors (enough jobs are waiting for execution), lightly loaded processors(less jobs are waiting) and idle processors (have no job to execute). By load balancing strategy it is possible to make every processor equally busy and to finish the works approximately at the same time.

It has been shown that as more information is collected by an algorithm in a short time, potentially the algorithm can make better decision [ 15 ] . Dynamic load balancing is mostly considered in heterogeneous system because it consists of nodes with different speeds, different communication link speeds, different memory sizes, and variable external loads due to the multiple. The numbers of load balancing strategies have been developed and classified so far for getting the high performance of a system [ 15].

Researchers have proposed a numbers of load balancing strategies [23,25-33]. We have considered the diffusion algorithm for the load balancing. There are mainly two types of diffusion algorithms. In sender initiated diffusion (SID) algorithm an over loaded processor wants to send task to the under loaded processor by selecting a remote node in the network.

Three sender initiated algorithms have been proposed [25]. The first algorithm sent the load from overloaded node to the randomly selected node without considering the load situation there [25]. The second strategy sent the load from the overloaded node to the randomly selected node by including the concept of threshold load to prevent the load to reach the overloaded node [25]. In the last one, several nodes selected randomly and compare the load and target is the least loaded node [25]. Although no information is collected for the load transfer but the receiver may be far away from the sender and this may cause performance degradation due to the transfer cost. To overcome this problem, immediate neighbor state policy has been proposed which states that the receiver and sender would be adjacent to each other [32]. Receiver initiated diffusion (RID) approach is just the converse of sender initiated approach. An under loaded node initiates the load balancing in this scheme. In this strategy all the near-neighbors of the under loaded node inform their load and update the information. In RID approach the under loaded node which wants to transfer load does consider all the nearest nodes without knowing whether the node is ready to transfer the load or not. It has been shown that the total number of messages communicated for updating for load balancing for K – connected (K neighbors) system of N processors is equal to KN [32]. In our approach we do not consider the nearest node which does not interested in load transferring. This approach would reduce the over heads and always less than KN but in worst case our algorithm’s complexity merges with KN .

• III.    BASIC Notations

We have considered a homogeneous distributed network. All the necessary parameters related to distributed network are presented in tabulated form in Table 1. All the tasks are homogeneous and are of equal size. We considered three types of nodes as over loaded node (OLN), under loaded node (ULN) and moderate loaded node (MLN) and the classification of nodes depending upon the load on a node is shown in Fig. 1.

Table 1. Mathematical Notation for Distributed Network

Symbol	Description
G=(V, E)	Distributed Network
V={1,2,……,N}	Set of nodes in a distributed system
EGVxV	Set of edges
N	Total number of nodes in distributed system
n	Total number of under loaded nodes(ULN) in the system at a particular instant where n
li	Load of node i
L	Total load in the system
Lavg	Average load per node
Mn	Message communicated for collecting load information by n ULN
Di	Neighbors of node I denoted by Di = j\ j E V and (i, j) E E}
Ki	Numbers of overloaded nodes in Di of under loaded nodes
LDi	LDi is the amount of excess load of over loaded node in the domain of i

• IV.    Problem Formulation

In nearest neighbor algorithm all the directly connected nodes are considered for load transfer which causes more over head because it involves even the reluctant node. We consider just those nodes which want to participate either in sending or receiving the load. In our model we considered that the under loaded node will forecast its load status to the immediate nodes. We considered the global average load which can be calculated by (1). The most important fact is that the under loaded node will not communicate all the nearest nodes provided that the nodes are not overloaded.

LAVG - „

Where L = ^l.

n = 1

After calculating the average load globally, the processors will decide whether they are under loaded or overloaded or moderate loaded as shown in Fig. 1.

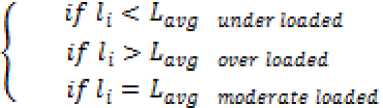
Fig 1. Classification of nodes depending on load

As it is the RID approach, the under loaded node will send the load situation to its immediate neighbors and acknowledgement will be sent by only overloaded processors. We have considered absolute load transfer rather than weight calculation [25]. In weight calculation approach all the neighbors are involved. Fig. 2 shows how a under loaded node (ULN) communicates with its domain under a particular situation. We designed an algorithm for getting the overheads by an ULN as shown in Fig. 3.

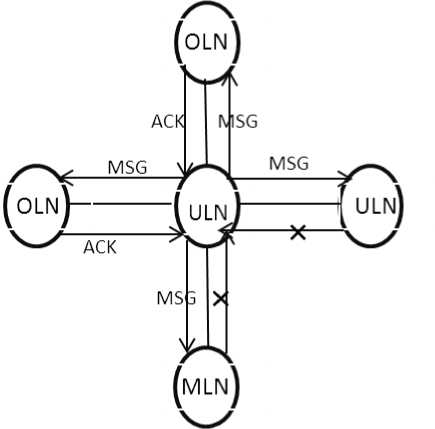
Fig. 2. ULN communicates with its domain at a particular moment begin:

N

Calculate L = ^ l i - ;

i = 1

Calculate Lm_ = —; avg N for any node i: 0 to n if (li < Lavg )

• l _i sends the update msg to D i ;

for any node lj e Di  /* Di = {/1 j e V and. (i, j) e f} */ if (lj > Lavg )  /* OLN in Di*/ for Ki e Di  /* Ki < Di */

K_i sends back ACK with LD j to l _i ;

end for end for end for end

Fig. 3. Algorithm for collecting communication overheads

• V.    Complexity

Number of message updated for load information by ULN is given by

Ctot (update) = NK                        (3)

lim M _n = ND i                        (4)

n -> N

Where the value of both D i and K i depend on the network topology. Marc Willebeck-Lemair and Anthonyhas given (3) [32]. We compared (2) with (3) and our equation reduces to (4) at n=N.

• VI.    Result And Discussion

We have considered Mesh topology in this paper. In mesh topology D ^ <  4 and K ^ <  4 . For inner node of mesh topology D i- = 4 and K ^ = ( 0,1,2,3,4 ) . For K _i =0, no load balancing would be done but D _i number of overheads per ULN would occur. In worst case our algorithm reduces to NK (or ND _i ) [32] when n=N. At n=N, K i =0. We considered worst case as the situation when K i =4. In our simulation we considered 20%, 30%, 40% and 50% of ULD in 4×4 and 16×16 mesh topology and results are tabulated in Table 2 and Table 3

respectively. Fig. 4 and Fig. 5 illustrate Overheads VS ULN. The simulation shows that as the numbers of ULN increases the value of K i goes on decreasing becausethere is a great probability to have more under loaded neighbors under the domain of an ULN. At 50% of ULN, M is fictitious in worst case as K i trends to zero. The converse is also true for an OLN. An OLN sends the message for load balancing to its immediate neighbors and the ULN under D i sends back the information about their load deficiency.

Table 2. Simulation Result for 4X4 Mesh Topology

n	Worst Case (Overheads)	Optimal (Overheads)
3 (20%)	24	19
4 (30%)	32	24
6 (40%)	44	28
8 (50%)	56	36

Table 3. Simulation Result for 16X16 Mesh Topology

n	Worst Case (Overheads)	Optimal (Overheads)
51 (20%)	408	398
76 (30%)	580	402
102 (40%)	752	462
128 (50%)	872	516

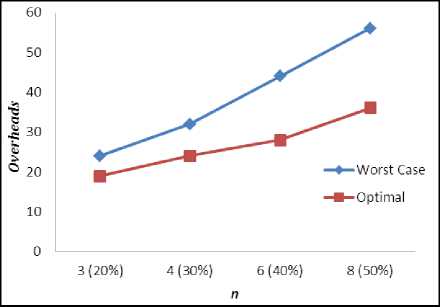
Fig 4. Overheads VS ULN in 4X4 mesh topology

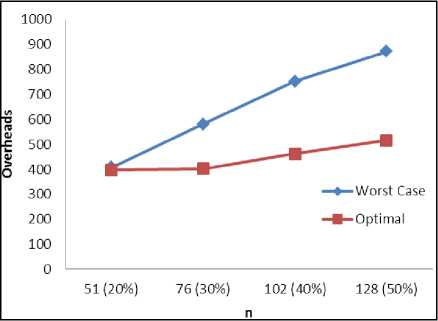
Fig 5. Overheads VS ULN in 16X16 mesh topology

• VII.    Conclusion

In distributed computing system some nodes are under loaded and some are over loaded and during the computation many fast nodes become under loaded while the slow nodes become over loaded due to the uneven distribution of load in the system. In distributed system, the most common important factor is to collect the information about load status on different nodes. The success of load balancing algorithm depends on how quickly the information about the load in the system is collected by a node willing to transfer or accept load. In this paper we have shown that the overheads depend on the number of OLN present in the domain of ULN and vice-versa by (2). Our simulation results show that the numbers of overheads communicated at a particular moment are fairly less than KN and our algorithm complexity merges with KN when the number of ULD is equal to N. Most important thing is that at 50% of ULN, the overheads becomes fairly less than expected due to the fall in the value of K_i. The value of K_i falls because there is a great probability to have more under loaded neighbors under the domain of an ULN and K i =0 when there will be no over loaded node in the network.

Acnowledgement