An Efficient Distributed Power Control in Cognitive Radio Networks

Published Online January 2016 in MECS

Nowadays, cognitive radio technology is influential in the efficient use of scare radio resources and frequency spectrum. In cognitive radio technology, spectrum is shared between licensed users and cognitive radio users in an opportunistic manner. In this technology, when licensed user or primary users (PU) do not use the frequency band, cognitive radio or secondary users (SU) are allowed to use it; but, while SU uses frequency band and PU also wants to use this band, there are two ways for SU:

• •    SU leaves that band and jumps to another existing spectrum band;

• •    SU stays in the same frequency band, but changes its power so that interference on the PU does not exceed a threshold.

Obviously, jumping to another frequency band causes an interruption for SU, because it has to find an empty one; therefore, it reduces performance for some of the users. Considering these issues, if we could control SU power so that interference on the PU does not cross a threshold, the second solution will be more appropriate.

There are two ways to control transmit power in cognitive networks: distributed power control and centralized power control. Since in distributed power control, the base station needs less local information and feedback, distributed power control is more preferable than centralized power control. One of the distributed algorithms which was proposed in [1] and used in the previous work (TPC-CBS) [2] is fixed-target-SIR tracking power control (TPC). By means of this algorithm, when the system is feasible, all the users reach their target SIRs with the minimum power. According to [3], [4], [5], and [6], this algorithm converges to a unique fixed point.

The TPC algorithm also has a drawback; its fixed target SIRs. In other words, using this algorithm while the system is feasible, all the users, with enough or extra sources, reach the same target SIR, which is not desirable. For instance, this fixed target SIR does not limit some of the services like voice (due to the characteristics of the service and human ears); but, for some services like data, reaching SIR beyond the least target SIR enhances the system performance. Hence, we should find another distributed power control algorithm to improve system performance. Moreover, another challenge in this cognitive network is related to determining user's power in a distribute manner, which should be controlled frequently so that SU interference in the PU does not exceed a threshold.

In this paper, we are going to use the algorithm in [7] while keeping the system feasible; not only all the users reach the minimum target SIR, but also those users who have more resources reach more SIR and, therefore, the system throughput improves in comparison to the previous work (TPC-CBS). Moreover, by means of fuzzy logic systems (FLS), this algorithm controls the power of SUs to use the frequency band without too much interference in the primary users.

The rest of this paper is organized as follows: In Section 2, the system model is introduced. In Section 3, first, drawbacks of the previous work are stated and, then, the proposed method for solving these drawbacks is discussed. Simulation results, related works and conclusions are presented in Sections 4,  5 and 6

respectively.

II. System Model

In this section, we consider a network with 4 primary cells and 1 cognitive radio cell.

In this network, к = { 1,2,..., K } and m = { 1,2,..., M } are the base station and active users, respectively. Each base station is assigned to a cell and each user receives service by a base station per second. Power used by each user i is shown by p . Noise is assumed to be additive white Gaussian whose power at the receiver of the base station k is г 2 . Base station assigned to user i is shown by S . If transmit power vector is shown by p = { p_x , p ₂,..., p_M } ,

SIR of each user i , which is denoted by y. is:

^{pihi ,s} i                         (1)

Y ( ) gi у (P) , where g is the processing gain for user i (defined as the ratio of the chip rate or (the spreading bandwidth) to transmit data rate) and h is equal to path gain between i,si user i and its assigned base station. The interference with user i 's base station is given by:

I. ( ^p ) = Е„ . p,h,. si⁺<          ⁽²⁾

power consumption should be controlled in order to prevent this interference from crossing a threshold.

In [2], TPC algorithm was used. The optimization problem of this algorithm is:

min

P >  0

L p.

i

subject to y ( P ) > Y

V i g M

This means users with the minimum power consumption reach their target SIR. While using this algorithm, all the users, whether with good channel or poor channel, reach a fixed target SIR, which is not convenient, because those users with more resources must reach higher SIR.

Thus, it is obvious from our optimization problem (5) in this paper that our concentration is on using distributed algorithm to power control so that those users with good channel reach higher SIR and, therefore, enhance the throughput. Also, for controlling SU interference in the PU, we use fuzzy logic systems (FLS) that helps identify the time period in which interference crosses a threshold and reduces SU's power. In optimization problem (5), I is SU interference in the PU and the threshold value of SU interference in PU is denoted by I^th .

max

P >  0

L t (p)

i

subject to y (P)> Y th

PU   PU

V i g M .

Similar to [8], [9], [10], and [11], we calculate the whole system throughput (sum of the throughput of all users) by:

T = L W log₂ ( 1 + y ( P ) ) ,         (3)

i where W is the channel bandwidth.

• 3.2 Proposed Method: EDPC Algor thm

When minimum acceptable target SIR is feasible, power control should be done so that all the users reach their minimum target SIR, and those users who have better channel reach higher SIR; hence, their throughput goes higher. Moreover, after user's power is determined in a distributed manner, conditions must be stable so that SU interference in the PU does not cross a threshold. Therefore, our proposed algorithm consists of two parts: determining user's power in a distributed manner and preventing the system from causing excessive interference in the PUs, which are described in the following sections.

• A) Determ ne D str buted User's Power

3.1 Problem Statement and Object ve

For determining user's power, DTPC algorithm is used. In this algorithm, each user like updates its power in a distributed manner in each iteration by:

III. Problem Statement and Proposed Algorithm

As mentioned in the previous sections, if SUs do not cause too much interference in the PUs, they can use the same frequency spectrum simultaneously. Hence, user's

f(D)(P (t ))=j

П

R.( p (t)) ’ ,гЛ(P (t)),

if R . ( P ( t )Y R t if R . ( P ( t ) ) > R t

where R th is effective interference threshold, ^ is

constant, and y is equal to minimum acceptable target SIR for user i .

It is obvious from (6) that, when a user has a bad channel ( R >  R* ), its SIR sets to the minimum target SIR and, when ir has a good channel ( RR ^th ), its SIR will be more than the minimum value.

B) Prevent System from Causing Excessive Interference on the PUs

Another challenge which is observed is that, if power of SU and PU is determined by DTPC algorithm, it might be possible that sometimes SU's power consumption causes excessive interference on the PUs (e.g. when the number of SU's users who are close to PU is increased or when the distance between SU and PU is decreased and so on). In our approach (EDPC), the time periods in which SU interference in the PUs crosses a threshold is identified by means of fuzzy power control system and the SU's power changes to the desirable value.

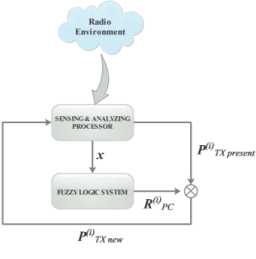
Fig.1 shows a fuzzy power control system that is used in our proposed algorithm (EDPC). It can be observed that, in this system, SU interference in the PU which is shown with linguistic variable x is given to FLS as an input. Then, according to x value which is low, moderate, or high, transmit power control ratio (R) will be determined. For instance, if interference is low, R is high, if interference is high, R is low, and if it is moderate, it does not change.

After defining R as the output of FLS, by multiplying this value by the current power of user (which is calculated by distributed algorithm DTPC in Section 3.2-A), the new transmit power value for the user will also be determined.

-150 -130 -110 -90 -70 -50  -30  -10   10  30  50

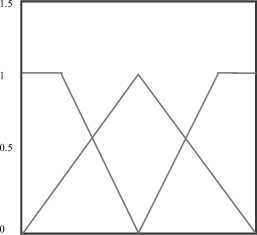
Fig.1. Fuzzy power control system for cognitive network and the membership functions used to represent the linguistic variable x.

To fully assist the task of collecting information about the interference level, it is recommend to estimate the interference level P ^{( i )} (caused by the i ^th SU) by the reclaiming PU. The estimated value is then immediately sent to the primary BS which is managing the PU. Then, the primary BS stores this estimated value in a real time database which can be accessed by the secondary BS. Now, SU can refer to this database and achieve to that estimated value via a common control channel.

Considering the above issues, new transmit power of user i p ⁽ i ) could be calculated by:

TX new

P ⁽ i )   = R⁽ i Vp⁽ i )                   (7)

^P TX new    R PC ^P TX Present ^{,              (7)}

where r ( i ¹ is transmit power control ratio for user i and P ⁽ i )    is equal to transmit power level for user i which

TX Present is calculated in a distributed manner in Section B-1. We can define P(*) to dB domain by:

TX new

^P TX L ( ^dB ) = 101og ^R PC- PX Pr„ ,               (8)

= R ⁽_P i_c ¹ ( dBm ) + p 1\^ ( dBm ) .

• IV.    Simulation Result

• 4.1    Comparing EDPC with Existing Method in terms of Power Control

In this section, we will evaluate the proposed algorithm EDPC and observe how the primary and secondary users' power could be determined so that not only performance is improved in comparison with TPC-CBS, but also it is guaranteed that SU interference in the PU does not cross a threshold in the case of using the same frequency band by the primary and secondary users at the same time.

We assume the processing gain of 100. The additive white Gaussian noise power at the receiver, i.e. σ2, is assumed to be -113 dBm. As in [12] and [6], we adopt a simple model h. = kd -4 for the path gain, where d. is i              i,si                                                                  i,si the distance between user i and its base station s , k is the attenuation factor that represents power variations, and k =0 .09. In our simulations, we take the target SIP П = 1 (as in [13] and [14]) for all the users. The values of Y are the same in TPC-CBS and EDPC.

In the presented simulation, a four-cell primary network along with the CRN is considered which includes 20 users indexed from 1 to 20. An example of such a four-cell network is shown in Fig.2.

In this section, our proposed method will be compared with the existing method which uses TPC algorithm.

As illustrated in Fig.3, when minimum target SIR is feasible, if PU and SU powers are set by TPC algorithm, all users reach the minimum target SIR with minimum power consumption. Although some users (e.g. user1) which are close to their base station have more resources than other users, their SIRs are similar. As can be observed in Fig.4, if the proposed algorithm, i.e. EDPC, is used for power control, those users with more appropriate channels (e.g. users 19,1) reach higher SIR and other users with poor channels reach the targeted SIR.

In Table 1, it is observed that, in the proposed method, SIR of users 1 and 19 is higher than the minimum target SIR. Therefore, in EDPC approach, throughput is improved to 21 percent in comparison with the previous approaches (TPC-CBS).

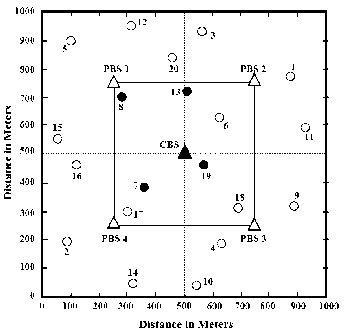
Fig.2. User and base station locations. Primary and secondary users are marked with ‘ о ’ and ‘ • ’ each respectively, and primary and secondary base stations are also marked with ‘ △ ’ and ‘ А ’.

• 4.2    Interference Control in the PU Using Phase System

After depicting the superiority of EDPC performance compared with TPC-CBS, we must show that using fuzzy logic systems (FLS) could guarantee that, when SUs use the frequency band, their interference in the PUs does not cross a threshold.

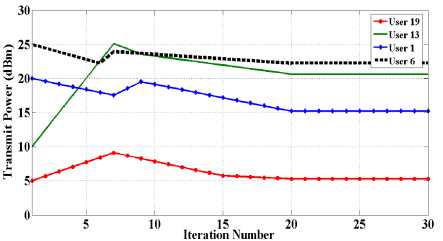
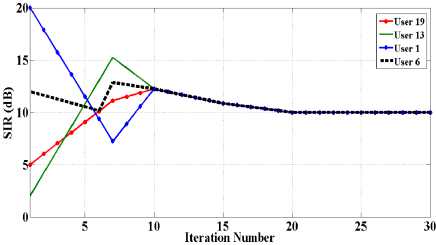
Fig.3. Transmit power and SIR of all users in TPC-CBS algorithm.

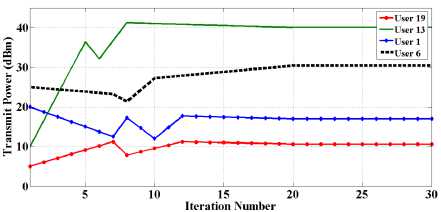
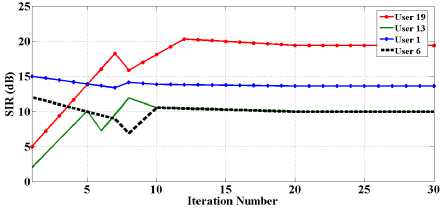
Fig.4. Transmit power and SIR of all users in EDPC algorithm.

Table 1. The value of transmit power and SIRs where the algorithm converges for both TPC-CBS and EDPC algorithm.

User	TPC-CBS		EDPC
	SIR	Power	SIR	Power
1	10	15.2312	13.6114	17.001
6	10	22.2312	10	30.4236
13	10	20.6312	10	40.0236
19	10	5.3123	19.4236	10.6589
Throughput		2.7653	3.4780

In Fig.5, which shows only CRN, suppose that user 19 wants to start to move at t=5s from P1 and at t=10s reaches P2. In Table 2, it is denoted that, when user 19 is at P1, its SIR reaches higher than the minimum target SIR (19.4236), because it is nearer to the base station and has a better channel capacity. However, while moving to P2, its SIR will be reduced to target SIR (10). Moreover, because of the increased distance from the base station, it has to increase transmit power and cause an interference in the primary user 6 to cross the threshold; therefore, user 6 will not be able to reach its preferable target SIR and this event is not acceptable, because PUs have higher priority than SUs. However, using the proposed algorithm, i.e. EDPC, which utilizes FLS, the power of user 19 is reduced. Hence, interference in primary user 6 will be less than a threshold and, therefore, primary user 6 will also reach its target SIR (Table 3).

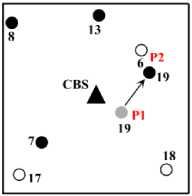
Fig.5. User and base station locations in cognitive radio network when user 19 moves from P1 to P2.

Table 2. The value of transmit power and SIRs for users 6 and 19 when user 19 moves from P1 to P2 in TPC-CBS algorithm.

User         t=5t=10

SIR    Power    SIRPower

19    19.4236   10.6589   14.2354   17.2347

6       10     30.4236     8.945

Total Number of Primary Users

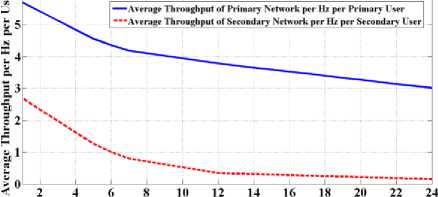
Fig.7. Average system throughput of the primary network per hertz per primary user and the average system throughput of the CRN per hertz per secondary user versus the total number of primary users when primary and secondary users employ EDPC.

Table 3. The value of transmit power and SIRs for users 6 and 19 when user 19 moves from P1 to P2 in EDPC algorithm.

User         t=5t=10

SIR    Power    SIR    Power

19    19.4236   10.6589   12.3453   13.2347

6       10     30.4236     10     36.7620

Fig.6 also shows the value of average transmit power and SIR (the sum of transmit power consumed and the sum of SIRs received by secondary users divided by the total number of secondary users, respectively) toward increasing primary users. It can be observed that, by increasing the number of PUs, transmit power for SUs is decreased; therefore, their SIR will also decrease, which means the throughput will decrease considerably.

Moreover, as can be observed in Fig.7, average system throughput of the primary network per hertz per primary user (the sum of throughput values for all primary users divided by the allocated bandwidth and the total number of primary users) and the average system throughput of the CRN per hertz per secondary user (the sum of throughput values for all secondary users divided by the allocated bandwidth and the total number of secondary users) toward the increasing number of primitive users is considered in the proposed algorithm. It can be observed that, in this proposed method and using FLS, SUs will not have any interference impact on Pus, which does not decrease the throughput.

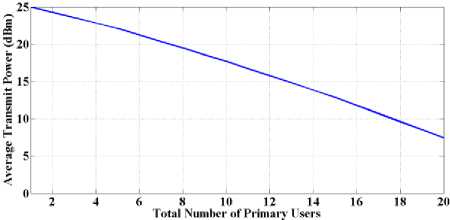
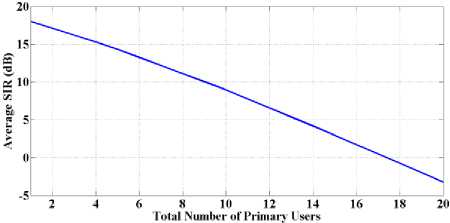
Fig.6. Average transmit power and average SIRs versus the number of primary users when primary and secondary users employ EDPC

• V.    Related Works

In the fixed-target-SIR-tracking power control algorithm (TPC), each user tracks its own predefined fixed target SIR. With TPC that was proposed in [1] users are able to achieve their fixed target SIRs at minimal aggregate transmit power when target SIRs are feasible. However, original TPC suffers from a major drawback [15]. It makes users to exactly hit their fixed target SIRs in feasible system, even when additional resources are available which can be used to achieve higher SIRs (and better throughput values).

Moreover, opportunistic power control (OPC) allocates high power to users with good channels (i.e., high path gains and low interference levels) and allocates low power to users with poor channels. In this algorithm, a small difference between two users in gaining paths may lead to a big deviation from their actual throughput values [13], [16]. Since an opportunistic algorithm always favors those users with better channels, it magnifies unfairness. For users with low mobility (when their channels slowly vary or are static), this might lead to long-term unfairness.

To optimize the system throughput for a given lower bound SIR, in [7], a distributed dynamic target-SIR tracking power control algorithm (DTPC) was proposed for wireless cellular networks by using TPC and OPC in a selective manner. In DTPC, when the effective interference (the ratio of the observed interference to the path gain) is less than a given threshold for a given user, this user opportunistically sets its target SIR (which is a decreasing function of the effective interference) to a value higher than its minimum acceptable target SIR; otherwise, it fixes its target SIR at its minimum acceptable level.

• VI.    Conclusion

In this paper, the distributed power control in cognitive radio networks was considered.

One of the drawbacks of the previous method (TPC-CBS) is fixed target SIR. Therefore, using the proposed EDPC algorithm, we could control the power of primary and secondary users while system is feasible. It means that those users with better channel reach higher SIR than the minimum target SIR and other users also reach their target SIR. As a result, throughput is increased considerably in comparison with the previous method. Moreover, to use the frequency band by primary and secondary users simultaneously, fuzzy logic system (FLS) is utilized to prevent interference in the primary users crossing a threshold.