An Efficient Graph-Coloring Algorithm for Processor Allocation

Published Online June 2013 in MECS

The configuration of a distributed computing system involves a set of cooperating processors communicating over the communication links. A distributed program running in a distributed computing system consists of several modules that need to be allocated to the processors and inter-communicate through the links for the completion of program execution. To improve the performance of a distributed computing system, several issues arise such as the minimization of execution and communication cost [1, 2, 3], the maximization performance of multiprocessors through maximization of CPU utilization [4]. Meanwhile, resource constraints may be imposed by memory size of processors and capacity of communication links.

In this paper, a graph-coloring algorithm based on (FMIS) is proposed to be used in the distributed system to build a multiprocessor allocation system, which capable of allocating one process at a time for each idle processor. A sequential technique for allocating processes is used to distribute processes among processors. The basic idea of the proposed algorithm is to select a node with maximum degree first, based on the previous garph-coloring alorithm FMIS [8]. The proposed algorithm has been constructed by using some modifications of the FMIS algroithm. The experimental results reveal that the proposed algorithm produces better performance in terms of CPU utilization, and minimum time for coloring the graph, and produces minimum number of colors needed to color any given conncted garph by finding the number of Maximum Independet Sets [MIS]. The algorithm takes a polynomial time complexity.

During processes allocation, Graph Coloring technique will represent the busy processor at a specified time slot by generating a full directed graph, which in result, busy processors will be mapped in the graph with different colors for each.

This paper will be able to answer the following questions: Which processors are allocated? Which processors are idle? What is the number of allocated processors in specific time? What is the number of idle processors in specific time? What is the total number of allocated processors? What is the total number of idle processors?

The rest of the paper is orgainzed as follows: Section-2 presents relevant definitions and specifications on Graph Coloring. Sections-3 presents relevant background information on Multiprocessors Allocation System. Section-4 presents the proposed ColoringGraph algoithm. Section-5 reports on experment results. Finally, Section-6 discusses conclusions and future work.

• II.    Graph Coloring

An undirected garph G = (V, E) is a pair of finite sets, where V contains the vertices of the graph and the set E contains its distinct unordered edges [5, 6]. Two vertices of a graph are considered adjacent if an edge exists between them. An independent set (I) is a subset of vertices in G such that no two vertices in I are adjacent. The Maximum Independent Set (MIS) of G is an I with maximum cardinality among all I sets of G [5, 6]. The MIS problem is to find an I with the largest number of vertices in G. The problem of finding MIS in a given graph is very important in graph coloring and process allocation in a distributed susyem [7].

A Coloring of a graph is an assignment of positive integers called colors to its vertices such that no two adjacent vertices receive the same color. Finding a coloring of a graph that minimizes the number of colors is an NP-hard problem. However, this paper proposes an efficient exact Graph-Coloring algorithm based on finding the Maximum Independent Set (MIS), and modifying the existing FMIS algorithm [8], for getting the number of allocated processors and the number of idle processors in a distributed system.

• III.    Multiprocessor Allocation System

This paper aims to get a maximum performance of a multiprocessor system by maximizing CPU utilization, which is maximizing the number of CPU cycles actually executed on behalf of user jobs per hour of real time. Maximum CPU utilization is another way of saying that CPU idle time is almost to be very small. When in doubt, make sure that every CPU has something to do.

Processors

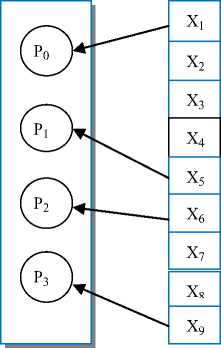
Processes

Fig. 1: Multiprocessor system with maximum CPU utilization

Fig.1 shows an example of a multiprocessors system with maximum CPU utilization, and may be overloaded. Fig.2 shows an example of an idle multiprocessors system with minimum CPU utilization. The proposed algorithm produces better performance in terms of CPU utilization and minimum time for graph coloring.

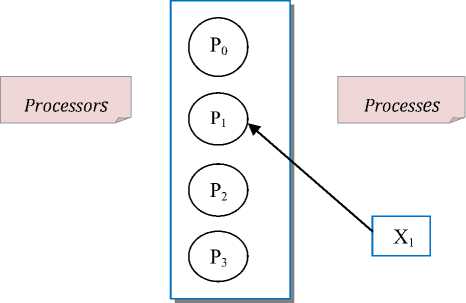
Fig. 2: Multiprocessor system with minimum CPU utilization

• IV.    The Proposed Algorithm

The proposed algorithm is based on the latest algorithm for finding Maximum Independent Sets (FMIS) [8]. This research modifies the existing FMIS algorithm for getting the number of allocated processors and the number of idle processors in a distributed system. The main modifications of the proposed algorithm consists of three major steps: selecting the node that has the maximum degree first among all nodes of a given graph; add the selected node to approximated maximum independent set; delete the selected node and its neighbors from the graph. Repeat, Graph-Coloring procedure until the degree of the remaining graph nodes becomes zero [9].

Procedure Graph-Coloring(G, V)

Input: G(V, E)

Output: MIS

Global: int max_ind_set[];

Char visite_node[];

Select Max-Node;

Get_ind_set()

/* Function for getting the independent sets*/

{

While degree_node( G ) < > 0

/* Return zero, if the remaining nodes in G of degree zero*/

{

v:= select_node( G )

/* Find the node from graph G that has the maximum degree*/

G:= G-v-neighbors(v);

max_ind_set = max_ind_set U {v}

}

};

• Fig. 3: The proposed Graph-Coloring algorithm

Fig. 3 represents the proposed algorithm; this algorithm will be used to find the MIS sets, for finding the number of colors in any given connected graph, and compared to the FMIS algorithm in terms of CPU execution time and number of colors that generated from applying the two algorithms. Results of implementing the proposed algorithm will be shown in details in the experiments section.

It is easy to analyze the proposed algorithm in terms of complexity time. The while loop actually takes O(n), also the select-node function takes O(n). Therefore, the complexity time of the entire proposed Graph-Coloring algorithm is O(n2).

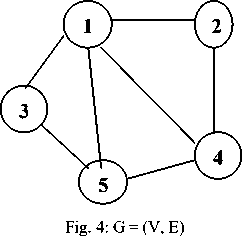
To understand the proposed algorithm, Fig.4 shows an example of implementing the proposed algorithm on graph G, which consists of five vertices.

Step-1:

Select the node that has maximum degree first and put it in max_ind_set[ ], as you see there is only one node, which is node-1, that satisfied this condition. Therefore, the MIS is {1}.

Step-2:

Delete the selected node and its neighbors from the graph.

Step-3:

After deleting node-1 and its neighbors, the remaining three nodes are of degree zero. Therefore, the MIS is {1}.

Step-4:

Delete the Maximum Independent Set nodes from the main graph, and repeat the algorithm again to find all coloring until the degree of the remaining graph vertices becomes zero.

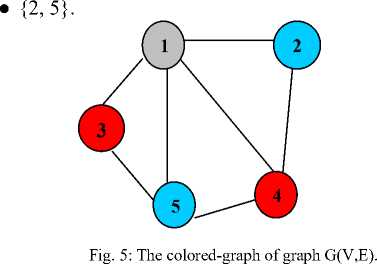
Fig.5 shows the colored-graph of graph G after implementing the proposed algorithm; there are only three colors needed for the entire graph G. Each of the following MIS sets represents a color:

• •    {1} MIS.

• •    {4, 3}.

• V.    Experiments

This paper reports experimental results that demonstrate the performance of the proposed algorithm. The algorithm has been programmed in Visual C++, and implemented on an Intel Core i7. The proposed algorithm will be applied, as an example, to the scheduling matrix shown in Fig.6. The matrix consists of eight processors, each of which with six time slots. The Xs indicate allocated slots, where as the number of output colors will express the number of allocated processors in a specific period. Each allocated processor has a direct communication link to every other allocated processor in the graph. Moreover, the proposed algorithm provides the ability to add or to allocate new processors, to allocate new processes, and to draw the graph coloring for allocated processors within each specific time slot.

		Processor
		0	1	2	3	4	5	6	7
н в л ю о	0	X	X	X	X	X
	1	X	X	X
	2	X	X	X	X
	3	X	X	X	X	X	X	X	X
	4	X	X
	5

Fig. 6: Scheduling matrix for eight processors

Table-1 shows results of implementing the proposed algorithm on the scheduling matrix shown in Figure-6. It can be noticed that the number of allocated CPUs is always equal to the number of colors in the resulted graph.

Table 1: Analysis for scheduling matrix

Time	No. of Allocated CPUs	No. of Idle CPUs	No. of Color	Allocated CPUs	Idle CPUs
0	5	3	5	{0,1,2,3,4}	{5,6,7}
1	3	5	3	{0,1,2}	{3,4,5,6,7}
2	4	4	4	{0,1,2,3}	{4,5,6,7}
3	8	0	8	{0,1,2,3,4,5,6,7}	{}
4	2	6	2	{0,1}	{2,3,4,5,6,7}
5	0	8	0	{}	{0,1,2,3,4,5,6,7}

According to previous scheduling matrix in Figure-6, the following results have been taken after implementing the proposed algorithm. Fig.7 to Fig.-12 shows the number of allocated processors. However, idle processors are not appearing in the resulted graph since the number of colors at each specific time slot represents only the number of allocated processors. Nevertheless, Table-1 also identifies the set of allocated processors and the set of idle processors. The ability of the proposed algorithm of coloring any connected graph with less time compared with the latest FMIS method is shown in Table-2 and Table-3.

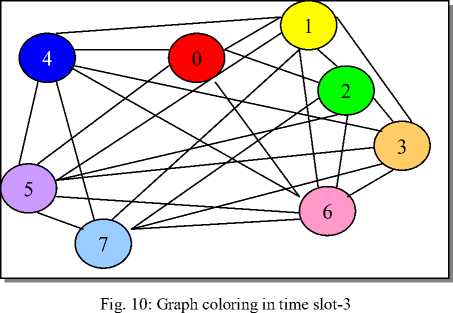
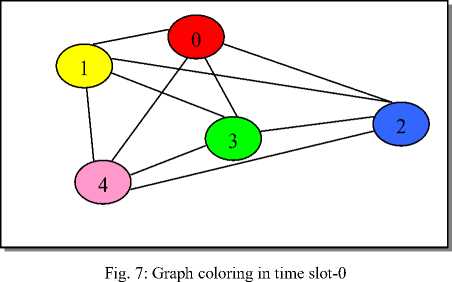
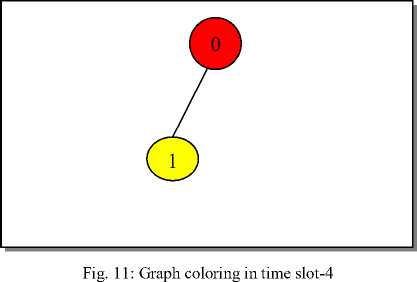
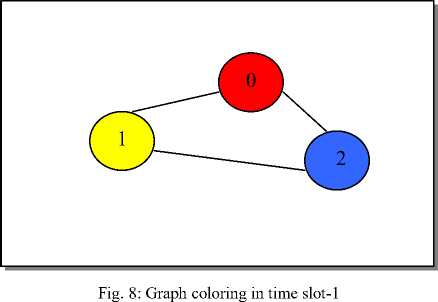
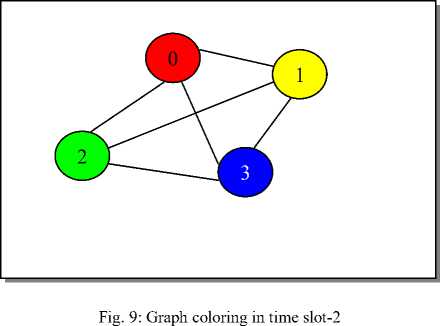
Table-2 show the average Graph-Coloring time resulted of running the FMIS algorithm in specific slot time with different graph densities (0.2, 0.5, 0.8), and different graph sizes (10, 30, 50, 70, 80, 100, … , 1000). Table-3 show the average Graph-Coloring time resulted of running the proposed algorithm in specific slot time with different graph densities (0.2, 0.5, 0.8), and different graph sizes (10, 30, 50, 70, 80, 100, … , 1000). Table-2 and Table-3 show that the number of allocated processors is always equal to the number of colors in the resulted graph.

It can be seen from Table-2 and Table-3 that the Graph-Coloring time and the CPU run time for the proposed algorithm is less than the graph-coloring time and the CPU run time for the FMIS algorithm. Moreover, the number of colors in the proposed algorithm is also less than the number of colors in the FMIS algorithm. As a result, the proposed algorithm gets maximum performance in terms of CPU utilization, and minimum time for of graph coloring.

It is also noticed from running the two algorithms that the execution time of the proposed Graph-Coloring algorithm is about half of the execution time of the FMIS algorithm. This is by itself a good contribution of the proposed Graph-Coloring algorithm.

Table 2: Analysis of the FMIS Graph-Coloring algorithm

No. of Processors	Graph-Coloring Time(sec)	No. of Allocated Processors	CPU Run Time(sec)	No. of Colors
10	0	5	0	5
30	0	7	0	7
50	0	9	0	9
70	0	10	0	10
80	0.01	13	0.01	13
100	0.02	16	0.04	16
150	0.04	21	0.15	21
200	0.231	35	0.24	35
500	1.482	66	0.873	66
1000	2.764	77	2.233	77

Table 3: Analysis of the Proposed Graph-Coloring algorithm

No. of Processors	Graph-Coloring Time(sec)	No. of Allocated Processors	CPU Run Time(sec)	No. of Colors
10	0	4	0	4
30	0	6	0	6
50	0	8	0	8
70	0	9	0	9
80	0	12	0	12
100	0.01	14	0	14
150	0.02	19	0.04	19
200	0.13	33	0.05	33
500	0.821	59	0.25	59
1000	1.562	70	1.032	70

• VI.    Conclusions and Future Works

This paper presents an efficient graph-coloring algorithm, based on finding the Maximum Independent Set (MIS). However, finding the MIS will be used for allocating processors in distributed systems. The proposed method has been constructed by modifying the FMIS algorithm. The proposed algorithm represents the allocated processors in specific time in a fully connected graph. The experimental results reveal that the proposed algorithm produces better performance in terms of CPU utilization, minimum number of colors, and minimum time for coloring the graph compared with the latest FMIS algorithm for finding MIS. For further studies, someone can improve the proposed algorithm to be able to detect defected processors by monitoring the graph.

Acknowledgements

The researcher would like to gratefully acknowledge the financial support of the Deanship of Scientific Research in Philadelphia University.