An Efficient Key Distribution Scheme for Sensor Networks

A Wireless Sensor Networks (WSNs) is a collection of sensor nodes with limited resources that collaborate in order to achieve a common goal. Since wireless sensor networks are usually deployed in a hostile environment, security is a critical issue [1]. Confidentiality, authenticity, availability, and integrity are typical security goals for WSNs. As the basic requirement for providing security functionality, key management plays central role in data encryption and authentication. When setting up a sensor network, one of the first requirements is to establish cryptographic keys. Researchers have proposed many key establishment protocols. However due to resource constrains of sensor nodes, many ordinary security mechanisms such as public key management schemes are infeasible in sensor networks.

The first practical key predistribution scheme was proposed by Eschenauer and Gligor [2], which refer as EG scheme. This scheme was based on random theory and probability theory. In this scheme, it generates a large pool of random keys and each sensor node is preconfigured a random subset of keys at the server prior to the network deployment. For every sensor node, a small fraction of keys, called key ring, is randomly selected from the key pool and is stored in its memory. Every two sensor nodes will have a certain probability to share at least one common key in their key ring. To improve the resiliency of this scheme, Chan et al.[3] extended the basic scheme in[2] requiring that two sensor nodes share at least q ( q >1) keys instead of just one common key to

* Author to whom correspondence should be addressed.

construct the shared-key used for further communications. It is illustrated, that, by increasing the value of q , the resilience against node capture would be improved. Du et al.[4] proposed another random key predistribution scheme that combined the basic scheme in[2] with Blom’s key pre-distribution mechanism[6]. In this scheme each node can pick rows from multiple secrete matrix. In this scheme, the keys in the key pool are treated as matrices. Liu et al.[5] proposed a similar pairwise key scheme based on Blundo’s polynomial-based key distribution scheme[7]. These two schemes exhibit a threshold: when the number of compromised nodes is smaller than security threshold, the probability of disclosed communication between non-compromised nodes is close to zero.

In [8], Camptepe and Yener applied combinatorial designs to key pre-distribution. They proposed two classed of combinatorial designs: symmetric-balanced incomplete block designs and generalized quadrangles. The points and blocks in the combinatorial designs are associated with the distinct key identifiers and nodes, respectively. Later, Sanchez and Balduls [9]made use of combinatorial design theory to the pre-distribution of multiple bivariate polynomial shares based on Blundo’s [6] key pre-distribution. This scheme enable direct key establishment for a large number of nodes, independently of the physical connectivity properties of WSNs. Lee and Stinson[10, 11,12] proposed a class of key pre-distribution schemes based on combinatorial designs. Their approaches improve the efficiency in direct-key and path-key establishments compared with the random key predistribution protocols.

In the existing key predistribution scheme, the pairwise keys between sensor nodes are generated by using the pre-load keys directly or derived from the preloaded secrete shares. Then once sensor nodes are captured, the adversary may crack other sensor nodes or even the entire network through the compromised keys or secrete shares. To address these problems, in this paper we proposed a key pre-distribution based on the EG scheme[2]. In our scheme, each sensor node randomly select two key pools from several key pools and picks keys from these two key pools. Compared with previous key pre-distribution schemes, our scheme can provide better resilience against sensor capture attack.

The rest of this paper is organized as follows. Section II overviews the Eschenauer and Gligor’s scheme in this paper. Section Ш describe our proposed scheme in detail. Section W deals with the detailed performance analysis. Finally, section V offers concluding remarks.

• 2.    background

• 3.    the proposed scheme

In this section, we overview the random key predistribution scheme proposed in [2] to provide the framework for more detailed description in the following sections. This scheme consists of three phases: key pre-distribution, shared-key discovery, and path-key establishment.

In the key pre-distribution phase, a large key pool S is generated first. Then, each sensor randomly selects m distinct keys from the key pool S , and stores them in its memory. This set of m keys is called the sensor’s key ring. The number of keys in the key pool, | S |, is chosen such that two random subsets of size m in S share at least on some probability p .

After the sensor nodes have been deployed, the key-setup phase will be performed. During this phase, each pair of neighboring sensor nodes attempts to find a common key that they share. Since all the keys are randomly selected from the same key pool, two sensor nodes may have some overlapped keys in their memories. If such a key exists, the key will be used to secure the communication link between these two sensor nodes. After the keysetup phase is complete, a connected graph of secure links is formed. Sensor nodes can then set up path keys with their neighbors with which they do not share keys. If the graph is connected, a path can always be found from a source sensor to any of its neighbors. The source sensor can then generate a path key and send it securely via the path to the target sensor.

The size of the key pool S is critical to both the connectivity and resilience of the scheme. For a given t , the larger the size of the key pool S , the lower local connectivity and the higher resilience. Local connectivity is defined as the probability that any two neighboring nodes share one key. Resilience is defined as the fraction of the secure links that are compromised after the adversaries capture a certain number of nodes

Now we describe how the proposed key predistribution scheme works in detail. The basic idea of our scheme is that the key setup server generates many key pools and each sensor nodes randomly selects two key pools and picks keys from these two key pools.

There are three phase in the proposed scheme: Setup Phase, Direct Key Establishment Phase, and Path Key Establishment Phase. The set phase is performed to initialize the sensor nodes by distributing key information to them. After being deployed, if two sensor nodes need to establish a pairwise key, they first attempt to do so through direct key establishment. If they can successfully establishment a common key, there is no need to start path key establishment. Otherwise, these sensor nodes start path key establishment, trying to establishment a pairwise wit the help of other sensor nodes.

• A.    The Predistribution Phase

In this phase, the key setup server first generates n key pools, then each sensor node random select two key pools from these key pools. At last, the sensor node picks t keys from each of these two key pools.

To identify each key, the identity of each includes two parts ( Id 1 , Id 2 ). The first Id 1 part is the identity of the key pool from which the key picks. The second part Id 2 is the identity of the key in the key pool

• B.    The Direct Key Establishment Phase

This phase initially takes place after the deployment of the network in the field. In this phase, if two sensor nodes want to establish a pairwise key, they need to identify a shared key. To discover whether a sensor node can establish the pairwise key directly with its neighbors, each sensor node broadcasts a list of key’s IDs to its neighbors. If they can find out at least one common key ID, they can use any of them as the pairwise key. Here the common key ID means the two part of key ID are all equal.

• C.    The Path Key Estabilshment Phase

• 4.    performance analysis and comparison

If direct key establishment fails, the two sensor nodes can establish pairwise key in the path key establishment phase. When a source sensor node broadcast the ID of a destination sensor node, an intermediate sensor node can establish a path key for the two sensor nodes if it holds the pairwise keys the source and the destination sensor nodes, respectively. Otherwise, the intermediate sensor node would broadcast this message continuously until it discovers a sensor node that shares a pairwise key with the previous sensor node and the destination sensor node respectively. Then the path key can be established along the message broadcast path reversely.

In this section, we give a detailed analysis of the above key predistribution scheme and compare with the other key predistribution scheme.

• A.    Local Connectivity

Local connectivity, which is probability of two sensor nodes establishing directly, is an important metric to evaluate a key predistribution scheme. To achieve a desired global connectivity, the probability of direct key establishment must be higher than a certain threshold value called the required local connectivity. Now we calculate the probability of direct key establishment.

Suppose there are n key pools. The probability of the two sensor nodes selecting two different key pools is P 1 ; the probability of the two sensor nodes selecting only one common key pool is P 2 ; the probability of the two sensor nodes selecting two common key pools is P₃ . We have

P 1 =

P ₂ =

P

(n А( n — 2'

V ² Л ² V

( n А

(n А

2 2 V 2 /V 2 /

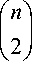
( ⁿ — ² А

V ² /

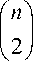
( " ^{— 2} 1

V 2 /(n 1V 2 /

( ⁿ — ² 1

V ² /

( n )

V ² /

( n А

V ² V

³    ( n А( n А   ( n А

n

n

V ² /V ²

v^v

V ² V

Suppose when two sensor nodes have one common key pool, the probability of the two sensor nodes selecting no common key from this key pool is p .

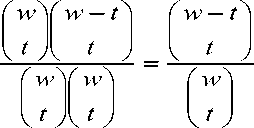
Let P c is the probability of any two sensor nodes sharing at least one key to form a secure connection. Then, P L =1-(probability that two nodes have no common key), hence

P L = 1

( n А

n

—

2 А

V

( 2 А( n

V ¹ J

n

—

—

—

n	n	n	n
2	V 2 V		2

1 А

V

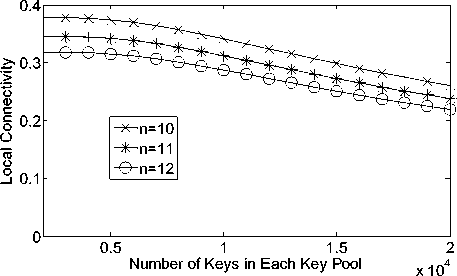
Figure 1 Probability of establishing pairwise keys directly for different g given t= 2 00

Figure 1 indicates that probability of direct key establishment in different size of key pool. In the simulation, we assume that each sensor node can store 200 keys. The results illustrate that the local connectivity decreases as the number of the key pools increase. This is that with more key pools the probability of two sensor nodes share common key pool will decrease.

• B.    Security Analysis

In this section, we evaluate how the proposed scheme improves the network security in terms of the resilience against node capture. We compare our scheme our scheme with some existing scheme by calculating the fraction of compromised communication among non-compromised nodes. We calculate the resilience of the scheme against the sensor node capture, which is the fraction of compromised network communication that is the disclosed communication among non-compromised nodes. To compute this fraction, we compute the probability of compromising the shared the keys between any two non-compromised nodes after x nodes have been compromised.

According to the scheme, we know that there are n key pools in the networks and each sensor node select two key pools. The probability that one compromised sensor node can disclose one key pool is 2/n. Hence, we have the probability P b , that any secure link between two uncompromised sensor nodes is compromised when x sensor nodes have been captured is

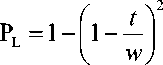
Number of Compromised Sensor Nodes

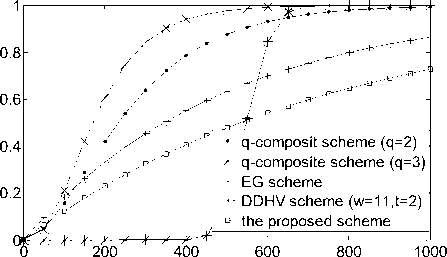
Figure 2 Fraction of compromised links between non-compromised sensor nodes v.s. Number of compromised sensor nodes (given local connectivity P L =0.33)

Figure2. shows the security performance of our scheme, the EG scheme [2] , the q- composite scheme[3], DDHV scheme[4] These figures clearly show our scheme have better performance than that in EG scheme and q -composite scheme. For example, in our proposed scheme when there 400 compromised sensor nodes, the fraction of the compromised link is 40%. the fraction of the compromised in EG scheme is 55%, that of in q- composite ( q =2) is 79%, that of in q -composite ( q =3) is 94%. Through the DDH scheme performs better than our scheme when few sensor nodes have been compromised, the adversary would control the whole sensor network once the number of the compromised sensor nodes is over the threshold. From there figures our scheme clearly has advantage over the EG scheme and the q -composite scheme and the DDHV scheme.

• 5.    conclusion

In this paper, an efficient key distribution scheme was proposed and numerically evaluated. In the scheme, the keys pre-distributed in each sensor node randomly selects two key pools from several key pools and picks keys from these two key pools. The effectiveness of the proposed algorithm has been demonstrated through analysis. Compared to exiting key predistribution schemes, our schemes is substantially more resiliency against sensor nodes capture.