An Efficient Pairwise Key Establishment Scheme for Sensor Networks
Автор: Xiaole Liu, Wangao Li
Журнал: International Journal of Education and Management Engineering(IJEME) @ijeme
Статья в выпуске: 7 vol.2, 2012 года.
Бесплатный доступ
Pair key establishment is a fundamental security service in wireless sensor networks (WSNs); it enables sensor nodes to communicate securely with each other using cryptographic techniques. However, due to the resource constraints, establishing pairwise keys in sensor networks is a challenging problem. Several key management schemes have been proposed in literature to establish pairwise keys between sensor nodes; they either too complicated, or insecure for some common attacks. To address these weakness, we propose an efficient pairwise key management scheme in this paper. In the proposed scheme, the sensor nodes are divided into groups and any compromised sensor node will not disclose the key information in the sensor nodes in same group. The analysis shows that compared with existing approaches, this proposed scheme has better network resilience against node capture attack.
Wirless Sensor Networks, Key Establishmentt, Key Space
Короткий адрес: https://sciup.org/15013722
IDR: 15013722
Текст научной статьи An Efficient Pairwise Key Establishment Scheme for Sensor Networks
Published Online July 2012 in MECS DOI: 10.5815/ijeme.2012.07.06
With major advances in the development of wireless and microelectronics technologies, it has become possible to deploy a large set of sensor nodes into a wireless sensor network (WSN) for large-scale event monitoring, data collection, and filtering. Wireless Sensor Networks consist of a large number of tiny sensor nodes which have limited computing capability and energy resource which can be deployed anywhere, and work unattended.[1] These characteristic poses security and privacy challenges for WSNs. Security is a critical issue as sensor networks are usually deployed in a hostile environment. Key management is crucial to the secure operation of WSNs. The goal of key management is to establish the required keys between sensor nodes that exchange data. Study of key management has been performed for many years. However due to resource constrains of sensor nodes, many ordinary security mechanisms such as public key management schemes are infeasible in sensor networks.
Corresponding author:
The basic random keys scheme is proposed by Eschenauer and Gligor in[2], which generates a large pool of random keys and each sensor node is preconfigured a random subset of keys from a large key pool before deployment of the network. Two sensor nodes can establish secure communication as long as they have at least one common key in their key rings. Later, Chan et al.[3] extended the basic scheme in[2] requiring that two sensor nodes share at least q ( q >1) keys instead of just one common key to establish a secure connection . The q-composite scheme increase the network resilience against node captures, but it is only advantageous when there is few captured sensor nodes. Based on basic scheme, Zhang et. al.[4][5] used Hash function to improve the capability of network to against nodes capture attack.
To improve security, two random key spaces schemes[6,7] have been proposed. In [6], Du et al. presented a pairwise key predistribution scheme combing the basic scheme in[2] and Blom’s key pre-distribution mechanism[8] together. Liu et al.[7] proposed a similar pairwise key scheme based on Blundo’s polynomialbased key distribution scheme[9]. These two schemes are very similar in nature, except that the key spaces are defined differently. In both schemes a number of key spaces are precomputed and each sensor nodes is associated with one or more key spaces before deployment. Two sensor s can compute a pairwise key after deployment if they have keying information from a common key space.
To achieve a better scalability, the group-based scheme[10,11,12] have been proposed. Du et al.[10] first employed sensor nodes deployment in the key pre-distribution. In the scheme, nodes are divided into groups, each of which is assign a sublet of key pool. Compare to the basic scheme [2], this scheme requires less memory to achieve an even higher connectivity because sensor nodes pick keys from a smaller subset of key pool. In[11,12], sensor nodes are grouped based on IDs to form horizontal and vertical groups. Any pair of sensor belongs to the same group are preloaded with a unique key before deployment.
In this paper, we will propose a new scheme in which the sensor nodes will be divided into groups. And all sensor nodes in the same group have a common key space and the sensor nodes in different groups have a probability to have a common key space. And any sensor nodes will not disclose the key information in the same group. Compared with previous key pre-distribution schemes, our scheme can provide better resilience against sensor capture attack.
The remainder of this paper is organized as follows. Section II overviews the background of the proposed scheme in this paper. Section Ш describe our proposed scheme in detail. Section W deals with the detailed performance analysis. Finally, section V offers concluding remarks.
-
2. Background
Blom in[9] proposed a key predistribution scheme which allows any pair of nodes in a network to be able do have a pairwise. It has the property that, as long as no more that λ nodes are compromised, all communication links of no-compromised sensor nodes remain secure.
In the Blom’s scheme, it assume some agree-upon ( λ +1)× N matrix G over a finite GF(q) , where N is the size of network and q > N . This matrix G is public information and may be shared by different systems. During the key generation phase, the system creates a random ( λ +1)×( λ +1)symmetric matrix D over GF(q) , and computes an N ×( λ +1)matrix A =( D·G ) T , where ( D·G ) T is the transpose of D·G . Matrix D must be kept secret, and should not be disclosed to adversaries or to any sensor nodes. Because D is symmetric, it is easy to see that
A·G =( D·G ) T ·G=GT·DT·G= GT·D·G =( A·G ) T
-
i .e., A·G is a symmetric matrix. If we let K = A·G , we know that K ij = K ji , where K ij it the element in the i th tow and j th column of K . The idea is to use K ij (or K ji ) as the pairwise key between sensor node i and sensor node j .
-
3. The Proposed Scheme
-
3.1. Setup Phase
Based on the random key predistribution scheme [2], Du et al. proposed an improved predistribution scheme using multiple key spaces (we call it the DDHV scheme)[6]. The DDHV scheme first constructs w spaces using Blom’s scheme and then each sensor node carry key information from t randomly key spaces. Now (from the properties of the underlying Blom scheme), if two sensor nodes carry key information from a common space they can compute a shared key. Of course, unlike Blom’s scheme, it can’t certain that any two sensor nodes are able to generate a pairwise key; instead (as in the basic random scheme), such a connectivity is probabilistic.
In this section, we describe how the proposed key predistribution scheme works in detail. The basic ideal of the proposed scheme is that all sensor nodes in the networks are to divide the sensor nodes into groups, and all nodes in the same group share a common key space and the nodes in two different groups have a certain probability to share a common key space.
Here, we divided connections among sensor nodes into two types, in-group and inter-group connections, depending on whether nodes are from the same group or not, and build two types of key spaces for these connection respectively. These two types of key spaces are of the same size and only different in their purpose.
There are three phase in the proposed scheme: Setup Phase, Direct Key Establishment Phase, and Path Key Establishment Phase. The set phase is performed to initialize the sensor nodes by distributing key information to them. After being deployed, if two sensor nodes need to establish a pairwise key, they first attempt to do so through direct key establishment. If they can successfully establishment a common key, there is no need to start path key establishment. Otherwise, these sensor nodes start path key establishment, trying to establishment a pairwise wit the help of other sensor nodes.
The setup phase is done offline by a setup server before all sensor nodes have been deployed in a target field. It has the following steps:
Step1: The setup server randomly generates a ( λ +1)× N matrix G over a finite GF(q ) and a set of random ( λ +1)×( λ +1)symmetric matrixes D over GF(q) . Then the setup server computes N ×( λ +1)matrixes A =( D·G ) T as the key spaces. To identify the different key spaces, the setup server may assign each key space a unique ID. These key spaces are classed into two classes. One, which called in-group key space, will be used by sensors inside a group; the other, which called inter-group key spaces, will be used by sensors in different groups.
Step 2: The setup server divides the sensor nodes into different groups, and each group contains no more than λ sensor nodes. To identify group, each group has a unique ID.
Step 3: For each group, the setup server assigns the i th row of an in-group key space to all nodes in the group.
Step 4: For each sensor node i , the setup server picks a subset of key spaces, and assigns the i th of these key spaces to node i .
-
3.2. Direct Key Establishment Phase
-
3.3. Phase Key Estabilshment Phase
-
4. Performance Evaluation
-
4.1. Local Connectivity
This phase initially takes place after the deployment of the network in the field. In this phase, every node tries to discover whether it node can establish the pairwise key directly with its neighbors. To do this, each sensor node broadcasts a list of key space IDs to its neighbors. If they determine that they a common key space, they can establish the pairwise key directly as discussed in Section II.
In this phase, if direct key establishment fails, two sensor nodes can try to establish a pairwise key. To do this, the source sensor node will broadcast the ID of the destination sensor node. If a sensor node holds the pairwise key with the source and the destination sensor nodes respectively, it will establish a path key for this two sensor node. Otherwise, the sensor node will broadcast the message continuously until it discovers a sensor nodes that have pairwise keys with the previously sensor node and the destination node until it discovers a sensor nodes which shares the pairwise key with the previous sensor node and the destination sensor node. The path key can be established along the message broadcast path in the reverse direction.
In this section, we evaluate the security property and networks performance of the proposed scheme. Here, we compare the proposed scheme with the exiting key predistribution scheme in this section . We present our analytical result on the following two metrics: local connectivity and resilience against node capture.
Local connectivity Pc , which is the probability of two neighboring sensor nodes can establish pairwise keys directly, is an important metric to evaluate a key predistribution scheme. Suppose sensor nodes i and j are neighbor. Let E 1 ( i,j ) be the event that sensor nodes i and j are in the same group. E 2 ( i , j ) be the event that sensor nodes i and j are in the two different groups, E 3 ( i , j ) be the event that sensor nodes u and v have a common intergroup key space.
Let t is the number of the groups, so we have
Pr (E1( i, j)) =1 Pr (E2( i, j)) = 1 -1
t , and t
Let w is the number of inter-group key space generated by the setup server, and τ is the number of in-group key space inside a sensor node, so we have
P r ( E з ( i , j )) = 1 -
L : 1 2T ] v T A T z ( w Y w )
V T К T 7
According to the scheme in the setup phase, all sensor nodes in the common group have a common key space, so these sensor nodes will establish a pairwise key directly. Hence, the local connectivity P c is
PL = Pr (E1( i, j)) + Pr( E2( i, k)). Pr( E з( i, j))
1 a 1A =;+(1 -1}
-
( 2 ww 1 2T 1 v T Tv T z ( w 1Г w 1
V T 7v T 7
Figure 1 includes that the local connectivity decreases as the number of the inter-group key space increase and the number of group has little affect on the local connectivity. From the setup phase, we know that the maximum number of sensor nodes in the network that the scheme can support is λ * t . For example when t is 200 and λ is 200, the network size 400000. This network size can be used in most wireless sensor networks.
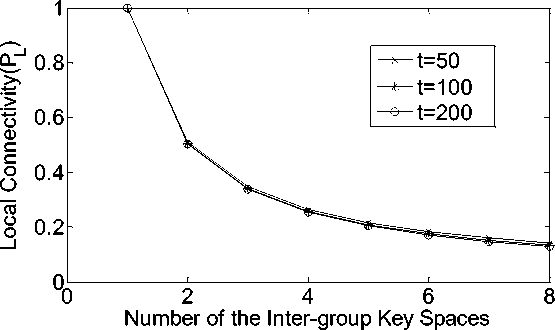
Fig. 1. Probability of establishing pairwise keys directly for different t given τ=1
-
4.2. Resistence against Node Capture
In a hostile environment, an adversary can carry out physical attacks on the sensor nodes and get the secret information from their memories. According to [6] , if more than λ sensor nodes, which use a common key space to generate pairwise key, have been compromised, this key space will be compromised. With the compromised key space, the adversary can eavesdrop not only the connections linked with the compromised sensor nodes, but also other additional ones secured by those keys which generated by the compromised key space. Sensor node capture attack is one of the most serious threats in wireless sensor networks. The resilience of the scheme is measured as the fractions of the total network communication that are compromised when x sensor nodes are captured.
According the mechanism of setup phase, we know that any in-group key space will not be shared more that λ sensor nodes. According prosperity of the key space in[6], the compromised sensor nodes have no affected on the secure of sensor nodes inside the same group.
Suppose there are x captured sensor nodes. Hence, we have the probability P b , that any secure link between two uncompromised sensor nodes is compromised when x sensor nodes have been captured is
x
p = E
i = n + 1
i " f n < i Д w ) I
—
n
w
x — i
Figure 2 show that the relationship between the fractions of compromised links for non-compromised nodes and the number of compromised nodes. We can see that the more number of sensor nodes compromised, the higher the fraction of compromised links.
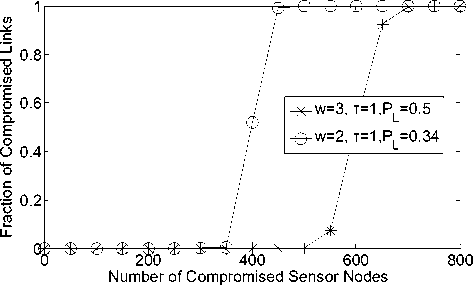
Fig. 2. Fraction of compromised links between non-compromised sensor nodes v.s. Number of compromised sensor nodes
-
4.3. Comparison with Previous Schemes
-
5. Conclusion
Now let us compare our scheme with the basic probabilistic [2], and the key space pool-based key predistribution protocol in (DDHV Scheme) [6].
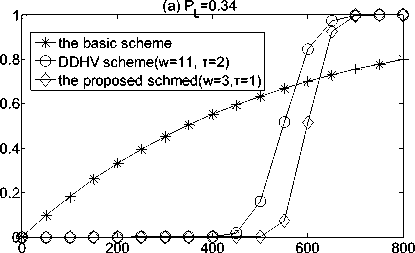
Number of Compromised Sensor Nodes
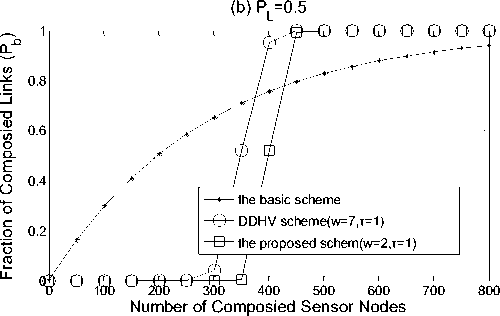
Fig. 3. Fraction of compromised links between non-compromised sensor nodes v.s. number of compromised sensors nodes. Assume each node has available storage for 200 keys
Figure 3. shows the security performance of our scheme, the basic probabilistic scheme [2] , and the DDHV scheme[6]. There figures clearly show that before the number of the number of compromised sensor nodes reaches threshold, our scheme performs much better than the basic scheme and q -composite scheme. When the number of compromised sensor nodes exceeds the threshold, the basic scheme has fewer compromised links than ours. Nevertheless, under such circumstances, none of these schemes provided sufficient security due to the large fraction of compromised links (over 60%). Thus, our scheme clearly has advantages over the basic scheme [2]. Compare to the DDHV scheme [6], from the figure we can clearly see that the threshold of ours is higher than that of the DDHV scheme.
In this paper, we proposed an efficient key pre-distribution scheme. In this scheme, we partition the sensor nodes into groups. All sensor nodes in the same group are surely can establish pairwise key directly and any compromised sensor nodes will not affect the security of other sensor node in the same group. Compared to previous key predistribution schemes, our schemes have better network resiliency against sensor nodes capture.
Список литературы An Efficient Pairwise Key Establishment Scheme for Sensor Networks
- I.F. Akyildiz, W. Su, Y. Sankarasubramanian. A survey on wireless sensor networks. IEEE Communication Magazine, 2002, 38(8): 102~114
- L. Eschenaure and V.D. Gligor, “A key-management scheme for distributed sensor networks”. in: Proc. of the 9the ACM Conference on Computer and Communications, Washington DC, USA, pp.41-47, Nov. 2002
- H. Chan, A. Perrig and D. Song, “Random key predistribution schemes for sensor networks”, in: Proc. 20003 IEEE Symposium on Security and Privacy, pp.197-313, May 2003
- J.Zhang, J.Li, X.Liu. A Strong Key Pre-distribution Scheme for Wireless Sensor networks. in: 2009 International Conference on Networks Security, Wireless Communication and Trust Computing. NSWCTC, 2009. Wuhan, Hubei, pp.231-234, Apr.2009
- J.Zhang, Q.Cui, X.Liu. An Efficient Key Management Scheme for Wireless Sensor Networks in Hostile Environments. in: International Conference on Multimedia Information Networking and Security, 2009, Hubei, pp.417-420, Nov.2009
- W.Du, J. Deng, Y.S. Han, P.K. Varshney, J. Katz, and A. Khalili, “A pairwise key predistribution schemes for sensor networks networks”. ACM Transactions on Information and System Security, Vol.8. No2,May(2005)228-258
- D. Liu, P. Ning, and R. Li, “Establishing pairwise keys in distributed sensor networks”. ACM Transactions on Information and System Security, vol.8, pp.41-77, Feb. 2005
- R. Blom, “An optimal class of symmetric key generation systems. Advance in Cryptography”. London, UK: Springer-Verlag, pp.335-338 , 1985
- C. Blundo, A. D. Santis, A. Herzberg. S. Jutten, U. Vaccaro, and M. Yung. “Perfectly secure key distribution for dynamic conference”, Information and Computation, vol.1, pp.1-23 , Jan. 1995
- W.Du, J.Deng, Y.S.Han, S.Chen, and P.Varshney, “A key management sechmes for wireless sensor networks using deployment knowledge”, in: Proc. of IEEE INFOCOM’04, 2004
- D.Liu, P.Ning, and W.Du, “Group-based key predistribution in wireless sensor networks.”, in: ACM WiSe’05, Proceedings, 2005
- L.Zhou, J.Ni, and C.V. Ravishankar, “Efficient key estsablishment for group-based wireless sensor deployments.”, in:ACM WiSe’05 Proceedings, 2005.


