An Image Thresholding Approach Based on Ant Colony Optimization Algorithm Combined with Genetic Algorithm

Published Online April 2015 in MECS

In the filed of image analysis and computer vision, image segmentation is a primary task of dividing a whole digital image into non-overlapping regions such that each region is homogeneous and the union of two adjacent regions is heterogeneous, the goal of which is to simplify the representation of an image that is easier to analyze or to extract some high level information[1][2]. The result of image segmentation is a set of segments collectively cover the entire image. Each of the pixels in the segment is similar with respect to some characteristic, such as color, intensity, or texture [3-4]. Image segmentation is one of most difficult low-level image analysis tasks and has attracted a mass of attention. A great deal of segmentation methods have been presented to handle with all kinds of images, such as Bo Peng has presented a region merging algorithm [5]. F. Y. Shih etc have put forward an automatic seeded region growing algorithm [6]. Palmer et al. used Sobel operators to extract image edges [7]. Barghout, Lauren, and Jacob Sheynin applied K-means algorithm to complete image segmentation, [8]V. Caselles, R. Kimmel, and G. Sapiro used a partial differential equation (PDE)-based method for image segmentation and so on[9]. In sum, segmentation methods in the literatures may be summarized as following main categories: clustering based methods, histogram based methods, edge detection, region growing methods, graph partitioning methods and thresholding based method etc. [1-10].

In common, as for an image, the gray levels of pixels belonging to the object are substantially different from the gray levels of the pixels belonging to the background. Thus thresholding is the simplest and effective method of image segmentation [1-2]. The output of the thresholding operation is a binary image whose one state will indicate the foreground objects, at the same time the complementary state will correspond to the background. The fundamental work of thresholding method is to choose an appropriate threshold value. Several popular methods are used in practice including the maximum entropy method, Otsu's method, Fisher criteria based method etc.[1-2],[10-20] .

Threshold selection methods may be classified into two groups, namely, global methods and local methods. A global thresholding technique shall partition the entire image with a single threshold value obtained by using the gray level histogram. Typical thresholding methods are mean method, P-tile method [2], etc. As for Mean method, it may be applied in very limited range, and as for P-tile it is hard to know prior information of the object or background. In general, threshold selection may be carried out with the histogram. In an ideal condition the histogram has distinct valley and peak. The gray level at the bottom of the valley could be used as a suitable threshold value. In practice, the above hypothesis is hard to exist. As a result, most threshlding methods are to build a model with certain discriminant criterion then search a gray value in the range of image gray scale to achieve image thresholding. However, these methods are based on 1-D histogram and don’t take advantage of any space adjacent information, which are easily ruined with noises and could not obtain anticipated results. In order to improve the performance of thresholding, some modified thresholding based on 2-D histogram are put forward. For example, Abutaleb proposed a 2-D entropic thresholding method based on 2-D histogram [12]. L. Li, J and TANG Yinggan present 2-D Fisher criteria based thresholding method[15-16]. A 2-D maximum entropy method was realized in[17]; moreover, a 2D Histogram and Maximum

Tsallis Entropy method was realized in [18]. A 2-D Otsu method was also implemented in [19-20]. All these methods could obtain better results than 1-D histogram based thresholding methods. However, the shortcoming concerned with 2-D histogram based thresholding method is that these methods require a lot of computation, thus efficiency was broken down. Ant colony optimization algorithm (ACO) is a probabilistic technique for solving computational problems, have been applied to many combinatorial optimization problems, ranging from quadratic assignment to protein folding or routing vehicles stochastic problems, multi-targets and parallel implementations [21-25]. The primary ACO is to deal with discrete optimization problem, in [26-28], binary coded ACO is presented to handle with continuous optimization problem. These ACO methods do not make use of any heuristic information, which may be further improved through combing with genetic algorithm. In this paper, an image thresholding approach based on ant colony optimization algorithm combined with genetic algorithm which uses 2-D Fisher criterion function as thresholding criterion is proposed.

The reset of the paper is structured as following. Section2 describes the thresholding approach based on 2D Fisher linear optimal discriminant analysis. Binary coded ant colony optimization algorithm combined with genetic algorithm is presented in section 3. In section 4, the idea of application the modified Binary coded ant colony optimization algorithm to obtain the best threshold values for 2-D Fisher criterion function is illustrated. Experimental results are given in section 5; in the end, the paper is concluded in section6.

II Two-dimensional Higorithm based thresholding

METHOD

Fisher's linear discriminant analysis is a classical classification method, which projects high-dimension data into a single line and conducts classification in 1-D space. It is to seek a linear transform that is able to reduce the dimension of a given n- dimension statistical model consisting of K classes to d ( d <  n) dimensions [15-16].

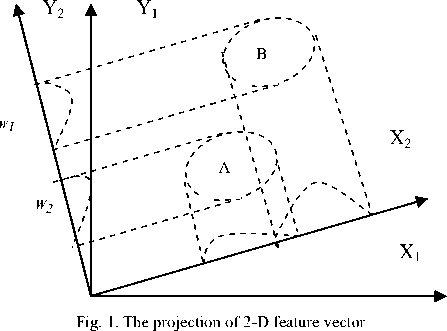
The transform shall meet the condition such that a maximum amount of discrimination information is kept up in the lower dimensional model and it tries to hold distance of already divided classes, which may give rise to a large overlap or even occlusion of neighboring classes, see Fig.1. There is condensed information of class in two scatter matrices, i.e., the between-class scatter and within-class scatter. The fisher criterion is formatted as blow.

J ⁽ w ) =

m_x — m 21² 22 s , + s^

In (1) m represents a mean value, s2 represents a variance of a class, and the subscripts stand for 2 classes. The transformation L may be acquired through maximizing (1), which means that the between-class scatter is maximum at the same time the within-class scatter is minimum, that is to say, the discrimination is optimal at this time.

\

In essence, thresholding is a classification problem which partition the pixels in an image into 2 two classes, one is the background and the other is the object, naturally, Fisher linear optimal discriminant analysis function may be used a thresholding criterion. Furthermore, to make use of part space information of the image, thresholding based on 2-D Fisher Criteria is presented and the basic idea of the method is as below [15-16].

Supposed F is an image with the size M x N and f ( x , y ) is the gray value of the pixel at position ( x , y ) . In order to compute the 2-D histogram of a given image we proceed as follow. Let the gray-scale of the image be L ( L = 0,1,...,255) . In a k x k neighborhood window, the average gray value of the neighborhood of each pixel is computed. Assumed that g(x, y) is the average of the neighborhood of the pixel located at the point (x, y). The average gray value for the 3 × 3 neighborhood of each pixel is calculated as (2).

k /2     k /2

g ^{( x} , У ) = -2 ^  ^ f ^{( x + m} , У ^{+ n} )         ⁽²⁾

^k m =- k /2 n =- k /2

where 1 <  x <  M ,1 <  y <  N, M and N are the width and height of the image, generally k=3 . The pixel’s gray value, f (x, y), and the average of its neighborhood, g(x, y), are used to construct a 2-D histogram

2-D histogram P ( i , j ) is defined as a joint probability mass function . Let r represent the integer part of the number r .The gray value f ( x , y ) and g ( x , y ) are used to constitute a joint pair. Let r be the frequency of pair ( i , j ) , where f ( x , y ) = i and g ( x , y ) = j then P ( i , j ) is computed as (3).

Pi =        ,1 <  i <  L ,  1 <  j <  L          (3)

ij  M x N

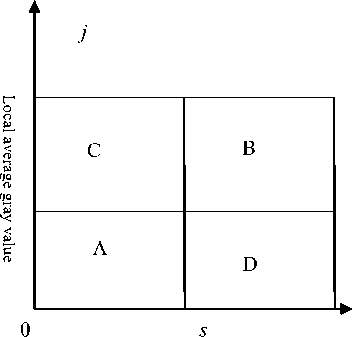
Pij is 2-D histogram of an image F , 2-D histogram is a matrix of size L x L which is as shown in Fig. 2.

In

t

i

Gray value

Fig. 2. Segments in 2-D histogram

Fig.2, 2 -D histogram is divided into 4 segments

according to thresholds ( s , t ) , where s , for f ( x , y ), represents the threshold of the gray level of the pixel and t for g ( x , y ), represents the threshold of the average gray level of the pixel’s neighborhood. Segment A and B denote the distributions of background and object class while segment C and D denote the distributions of pixels near edges and noise. On account of homogeneity, pixels interior to the objects or the background contribute mainly to the near-diagonal elements while the pixels of edges and noise contribute to the off-diagonal elements. Generally, the contribution of segment C and D may be neglected. Therefore, it may be assumed that p_y ® 0 for i = s + 1... L; j = 1,..., t and i = 1,..., s ; j = t + 1,...,L . Here, Segments A and B are taken in to account, which correspond to object and background respectively.

The mean and variance of the 2-D histogram of Fisher criterion could be computed by equations as below.

L E j * w (j) j     j=t+1 Ц1 =   L E w (j) j=t+1 (9) s о02i =E (i - A0 )2* H (i) i =0 (10) t o2j=E (j - A0)2* W (j) j=0 (11) L о; = E (i - A1)2* H (i) i=s +1 (12) L О12,. = E (j - A )2* W(j) j = t+1 (13) H (i) = E N (i, j ), i = 0,1,..., L -1 j=0 (14) W (j) = ]-; N (i, j), j = 0,1,..., L-1 (15) i=0

2-D Fisher criterion function is formulated as (16)

J f ( s , t ) =

([ Ц , A ] - [ A , A ])*([ a , A ] - [ A , A ]) )

2       2       2      2

О) , ⁺ О j + о + O 1 jj

Thus, optimal thresholds pair(s*,t*) can be achieved through maximizing (17).

( s , t ) = ArgMax ( J _F ( s , t ))                    (17)

^Ц 0 = ^{( ц} о , M q )

A = ( и ! ’ ^Ц 1 )

2  22

^О 0 = ( ⁰ 0 i ’ ^О 0 j )

0 -12 = ( ^ 2 О ²)

Where

E i * H ( i ) m 0 = ^----

i = 0

In common, despite what level of the image’s signal-to-noise ratio, 2-D histogram has two apparent peaks. As a result, it is easy to choose a suitable 2-D threshold ( s , t ) to segment the object from the background. However, this method may need hundreds of times of calculation than 1-D histogram based thresholding methods, which needs to be improved from the point view of efficiency. In the paper, the basic 2-D histogram based thresholding method will be improved with binary coded ant colony algorithm and genetic algorithm, fundamental of these 2 algorithms will be illustrated briefly in the following section.

t

E j * w ( j )

i j = 0

" 0 = —-----

E w ( j )

j = 0

A =

L

E i * H ( i )

i = s + 1

L

E H ( i )

i = s + 1

III Modified Binary ant Colony Algorithm

A. Binary coded Ant colony algorithm

Ant Colony Optimization (ACO) is a metaheuristic algorithm for solving hard combinatorial optimization problems proposed by Dr M. Dorigo in 1990s. ACO is based on the indirect communication of a colony of simple agents, called ants, mediated by pheromone trails. Nowadays, ant colony optimization has been applied successfully to a large number of difficult discrete

optimization problems including the traveling salesman problem, the quadratic assignment problem, scheduling, vehicle routing, etc., as well as to routing in telecommunication networks [21-22]. Much research results demonstrate that ACO has very strong ability to obtain good solutions to combination optimization and get good performance on parallel computing. Most applications of ACO are in the discrete domain[21-25]. Recently, more attention about how to use ACO in continuous domain has arisen and some binary coded ACO (BACO) have been put forward, which could be employed for continuous optimization problem [26-28].

Binary system is one of most effective data representation forms. 2-valued logic is easily simulated and realized. Moreover, the system has stronger robustness and ability of anti-interference. Supposed there is a binary network shown in Fig.3, we divide the work of ants, and different kinds of ants search the same routine, and pheromone is left on each edge. Each ant just chooses one edge of the two. Compared with the traditional ACO binary Ant Colony algorithm has the different route choice of ants. It can only choose 0 and 1 when the algorithm chose the route, the intelligent behavior of ant is very simple, and the incidence matrix traversed by each kind of ant needs only 2× n ’s space, which to some extent solves the descriptive difficulty generated from long coding and the reduction of solution quality[27-28].

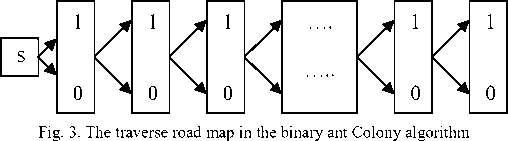
Definitions of a directed graph are given as below:

G =( C , L ), and the vertex set C is[27]:

c ₀( v_s ) c ₁( v_N ⁰) c ₂( v ¹ _N ) c ₃( v_N ⁰ _{- 1}) c ₄( v ¹ _{N - 1})

{,,,  ,  , c2N-3(v2)c2N-2(v2)c2N-1(v1 )c2N(v1)

,                        ,                       ,                   }.

The “ v ” is initial vertex. The “ v ⁰ ” and “ v ¹ ” are used to show the state of “0” and “1” in the binary encoding. For j =2, 3, ∙∙∙N, there are only two directed arcs which are the “ v ⁰ ” and “ v ¹ ” in the entire vertex.

These two directed arcs show the next state of every ant that are “0” and “1”. Each ant traversals all its route, and we can get the answer by the integration of every ant’s route. The steps of the binary ACO are the same as the Ant Colony Algorithm’s.

At the initial time, the concentration of pheromone is equal in the both route of “0” and “1”. Let τ (0) = V ( V is a constant), Δ τ =0(i, j=1, 2∙∙∙n). The ant “ k ” (k=1, 2∙∙∙, h ) decides the direction by concentration of pheromone in the different routes. The movement probability is as follows [26-28]:

p i^k , j (0) =

[ τ i , j (0)] ^α ⋅ [ η i , j (0)] ^β

[ τ i , j (0)] ^α ⋅ [ η i , j (0)] ^β + [ τ i , j (1)] ^α ⋅ [ η i , j (1)] ^β

p i^k , j (1) = 1 - p i^k , j (0)                               (19)

The “ pk ” is the probability of movement from the position “i” to the “j” at time t. The “α ” (α≥ 0 ) is the relative importance of the contrail and “ β ” ( β ≥ 0) is the relative importance of the visibility. The “τ (0) ” is the density of pheromone of the side which the “j” is “0”, while the “τ (1) ” is the density of pheromone of the side which “j” is “1”. The “η (0) ” is the visibility of the side which the “j” is “0”, while the “η (1) ” is the visibility of the side which the “j” is “1”. The ant decides the route by the concentration of pheromone on two sides. In addition, the pheromone will evaporate as time goes. Let τ (t + 1) be the intensity at time t+1, (t is iteration times) the trial information is updated as below.

L

τ _ij ( t + 1) = ρτ _ij ( t ) + ∑ Δ τ _i^l_j     i = 1,... N , j = 0,1    (20)

l = 1

Where ρ is a coefficient, whose value is in the range of [0 1] that (1- ρ ) represents evaporation. The value of Δ τ _i ^l _j is equal to F l , if value j is selected for i-bti of the solution built by ant and zero otherwise. Basic steps of BACO algorithm are as follows:

Step 1: generate the initial solution random

Step 2: judge whether the stopping condition is meet, if it is, output the best solution, or go to step3,

Step 3: ants search

Step4: compute the solution generated by ant colony algorithm, and reserve the optimal

Step 5: upgrade phenomenon of the net by optimal solution, go to step2

• B.    Genetic Algorithm

Genetic algorithm (GA) is a search heuristic that mimics the process of natural selection and evolution. This algorithm is routinely used to generate useful solutions to optimization and search problems especially there is not heuristic information of the problem to be handled, which is widely applied in bioinformatics, computational science, engineering, economics, chemistry, manufacturing, mathematics, physics, and other fields. In GA, a group of candidate solutions to an optimization problem is evolved toward better solutions.

A typical GA requires 2 basic factors: genetic representation of the solution domain and a fitness function to evaluate the solution domain. The main operations of GA are as following.

• a.    Initialization of genetic algorithm

Initially many individual solutions are randomly generated to form an initial population. The population size is dependent on the problem.

• b.    Selection

A generic selection procedure is implemented as below.

The fitness function is evaluated for each individual; then fitness of each individual is normalized. This step is repeated certain times until enough selected individuals are selected. In general, the roulette wheel selection rule is used in the step.

• c.    Crossover

Crossover is a main operator in GA used to vary the programming of a chromosome or chromosomes from one generation to the next. It is analogous to reproduction and biological crossover. Cross over is a process of taking more than one parent solutions and producing a child solution from them. Several Crossover techniques are used in GA, such as One-point crossover, Two-point crossover and Cut and splice etc. For example, the following 2 parents, the crossover position is at 4, a one-point crossover is carried out as blow [30].

Table 1. a sample of crossover operation
Parent1	1 1 0 1 0 0 0 1 0
Parent2	0 1 1 0 0 1 0 0 1
Children1	1 1 0 10 1 0 0 1
Children1	0 1 1 00 0 0 1 0

• d.    Mutation

Mutation is an operator utilized to keep diversity from one generation of a population of genetic algorithm chromosomes to the next. The most commonly used mutation operator involves a probability that an arbitrary bit in a genetic sequence will be changed from its original state.

• C.    Modified Binary coded ant colony optimization algorithm.

It is noted that the use of heuristic information is important for ACO algorithm, which gives the possibility of exploiting problem specific knowledge. In general, there is not heuristic information available in binary coded ACO, thus the performance of binary coded ACO is degraded. As is known Genetic algorithm does not need any heuristic information for problem to be handled. It does colony global searching quickly and stochastically, however, is not able to efficiently get to optimal results, since it slows down when solving to certain scope. On the other hand, ACO could obtain optimal results efficiently, but lacks initial pheromone at the beginning. As a result, a dynamic combination of genetic algorithm and ant algorithm was presented in [31], which had better performance than simple GA and ACO. In a similar way, GA could be with combined binary coded ACO, what's more, all these methods utilize binary encoding, which make them easy to be cooperated. The basic idea of modified binary coded ant colony optimization algorithm (MBACO) is as following. First, it uses genetic algorithm to generate preliminary search results of the problem to be handled. Then information of the results acquired is converted into initial pheromone distribution for binary coded ACO. In the end, the binary coded ACO are used to search for optimal scheme. The algorithm utilizes the advantages of the two algorithms and overcomes their disadvantages.

IV 2-D Fisher Criteria Thresholding Based on Modified Binary Coded ant Colonly Algorithm

This section will illustrate how to apply proposed hybrid optimization method for 2D Fisher Criteria thresholding method.

• A.    The scheme of proposed method

As is shown in section3, GA and BACO are coded with binary format. Therefore, it just illustrates how to encode the problem with BACO here. With regard to 8 bit gray scale images, the value of threshold is between 0 and 255, as for 2 thresholds, which could be encoded by 16 bits with the form of binary code. Hence, a solution made up with a string of Sb, S bj e {0,1} ,j=0,1,2,...15 ; each bit is with the value “0” or “1”. Using (21), solution string could be decoded into decimal threshold values.

• S = S b ₀ 2⁰ + Sb 2¹ + ... Sb 2⁷                 (21-1)

t = Sb 2⁰ + Sb 2 1 + ... Sb ₅2⁷                (21-2)

For example, a solution string Sb j is displayed as below

Table 2. Example of thresholds

1     1     0     1     1     0     1     1     0     1     1     0     1     0     1     0

In table2, the first 8 bits are on behalf of threshold1 , the rest 8 bits denote threshold2 .

• B.    Building a solution with binary coded ant colonly

In ACO, each uses make use of pheromone trail and heuristic information to build a solution. In the first, the pheromone matrix is set with a small value T , T denotes the pheromone concentration at the position i related to value j, in binary coed ACO, the value of j is “0” or “1”. With regards to solving the problem of mark N bits with 2 values, the size of pheromone matrix is N×2. By using of heuristic information provided with GA and pheromone trail, each ant could build a solution to the problem.

As the algorithm proceeds, the pheromone matrix evolves. Guided by modified pheromone matrix and heurist information, the ant colony could construct improved solution and above steps will go on until meets the terminal condition.

• C.    Fitness function

In general, the quality of the solution shall be measured by fitness function, in the paper; the goal of the proposed algorithm is to seek the maximum value of 2D Fisher Criteria of the image, hence, (17) is used as the fitness function.

Moreover, after implementation of ACO, to further improve the solution, a local search strategy is employed in the paper. That is, after ACO ends a quasi pair of threshold ( S , t ) is acquired. Then we make an exhaustive search in rang of (( [S-A], [S+A]), ([t-A, t+A] )) to decide the final optimal solution, in the paper, A is set as 5.

In short, the proposed method mainly comprises two steps, first, GA is used to create the initial solution; then the initial solution is applied to set heuristic information for BACO, and BACO is carried out further get the better solution.

• V.    Experiments and Discussion

To verify the effectiveness of the proposed method, it is tested on some images in this section. Moreover, to 2D Otsu method is also realized to compare segmentation performance with 2D Fisher Criteria base thresholding method. As for MBACO and GA, parameters are set as table3 and table4.

Table 3. Parameters used in GA

Parameter	Explanation	Value
N	Number of	50
Max_gen	Maximum iteration	20
Ps	Selection ratio	0.9
Pc	Crossover ratio	0.8
Pm	Mutation ratio	0.05

Table 4. Parameters used in ACO

Parameter	Explanation	Value
N	Number of ant(s)	5
Max_gen	Maximum iteration number	5
α, β	Relative importance of trail versus	1.0
ρ	Evaporation of pheromone	[0,1]

Because GA and ACO all are stochastic algorithms in essence, hence, the proposed method has been run 10 times for each image, experimental results are given in Table5-7 and Fig 3-Fig.6.

As is shown in table5-table7, the optimal pair of thresholds obtained by the proposed method with local search has no difference to corresponding optimal thresholds acquired by enumeration algorithm. As for 3images, the proposed method has acquired the optimal thresholds, see the data marked with “*” in table3. In addition, it is observed from table4, computing time of GA and MBACO is beyond 1seconds, at the same time, enumeration algorithm needs more than 5seconds to get the best thresholds, it is obvious that our method can reduce the computation time and enhance the efficiency. As is shown in table 4, MBACO is a little slower than GA; meanwhile, the fitness of MBACO is better than GA; that is MBACO has better optimization ability than GA.

Table 5. Thresholds obtained by using different methods

Image1	Exhaustion	2D Otsu	GA	MBACO
Person	165,168	65,56	164, 167	165,168*
Rice	137,141	133,138	138,140	137,141*
Man	151,154	254,255	163,163	151,153
Tank	204,208	61,60	201,205	204,208*

Table 6. computation time with different methods (Second)

Image1	Exhaustion	GA	MBACO
Person	6.339	0.6030	0.7539
Rice	6.520	0.6122	0.7885
Man	5.796	0.4460	0.5434
Tank	5.937	0.4549	0.5687

Fig.3-1 original image

Table 7. Fitness values of different methods

Image1	GA(*10-3)	MBACO(*10-3)
Person	0.3710	0.3722
Rice	0.2086	0.2094
Man	0.9948	1.0094
Tank	2.8319	2.8329

Fig.3-3 Proposed method    Fig.3-4 enumeration thresholding

Fig. 3. Man image and thresholding results

Fig.3-2 2D Otsu thresholding

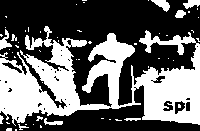
Fig.4-2 2D Otsu thresholding

Fig.4-3 Proposed method

Fig.4-4 enumeration thresholding

Fig. 4. Person image and thresholding results

Fig.5-1 original image        Fig.5-2 2D Otsu thresholding

Fig.5-3 Proposed method    Fig.5-4 enumeration thresholding

Fig. 5. Rice image and thresholding results

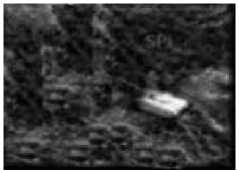
Fig.6-1 original image

Fig.6-2 2D Otsu thresholding

Fig.6-3 Proposed method

Fig.5-4 enumeration thresholding

Fig. 6. Tank image and thresholding results

As is seen from Fig.3-Fig.6, the proposed method could separate the object and background clearly especially when there is a main goal in the image, 2D Fisher Criteria based thresholding method is better than 2D Otsu based thresholding method.

• VI.    Conclusion

To sum up, to improve the performance of binary coded ACO algorithm, GA is used to produce the initial solution, then information of initial solution is used as heuristic information of ACO and ACO is executed for better solutions. The proposed method has been applied to solve the best thresholds for 2D Fisher Criteria based thresholding method. Experimental results show that the proposed method has good optimization ability and is able to seek the optimal threshold values for 2D Fisher Criteria based thresholding method. In addition, as is observed from the experimental results the 2D Fisher Criteria based threshold method outperforms 2D Otsu method when there is a single object image. In the future, the proposed method will be tested on more practical engineering optimization and other image processing problems.

Acknowledgment

This research was supported by National Natural Science Foundation 41301371 and 61202287, Department of Education of Hubei Province Q20121410, Doctor Fund of Hubei University of technology (BSQD13081 BSQD12032).